Este documento presenta un curso de cálculo financiero con el objetivo de capacitar a estudiantes en la formulación de modelos matemáticos básicos para resolver problemas financieros. El curso cubre temas como técnica mercantil, interés simple y compuesto, amortización de préstamos, anualidades, seguros de vida e inversiones a través de múltiples sesiones que incluyen conceptos teóricos y ejercicios prácticos.

1. Lic. Rosell Alejandro Valderrama Chumbes
Cálculo
Financiero
PROESAD
Programa de Educación Superior a Distancia
Mg. Luis Enrique Falcón Delgado

2. Título: cálculo financiero
Autor: Mg. Luis Enrique Falcón Delgado
Diseño interior: Doris Sudario S.
Diseño de tapa: Eduardo Grados S.
Responsables de edición:
Edwin Sucapuca Sucapuca, Christian Vallejos Angulo, Lizardo Vásquez Villanueva,
Mariela Malásquez Marín.
Primera edición, marzo 2012
El contenido de esta publicación (texto, imágenes y diseño),
no podrá reproducirse total ni parcialmente por ningún
medio mecánico, fotográfico, electrónico (escáner y/o
fotocopia) sin la autorización escrita del autor.
Universidad Peruana Unión - Facultad de Ciencias Empresariales
Programa de Educación Superior a Distancia PROESAD
Centro de Producción de Materiales Académicos CEPMA
Sede Central - UPeU
Carretera Central km. 19 Ñaña, Lima / Telf. (01) 618-6336 / 618-6300 / Anexo: 3084
www.upeu.edu.pe
e-mail proesad@upeu.edu.pe
http://proesad.upeu.edu.pe
Este libro se terminó de imprimir en los talleres gráficos del Centro de
Aplicación Editorial Imprenta Unión de la Universidad Peruana Unión,
Km. 19 Carretera Central, Ñaña, Lima-Perú
Telf.: 618-6301, Telefax: 618-6354
JOB 13969-12 UNIÓN®
E-mail: union@imprentaunion.com
Hecho el depósito legal
en la Biblioteca Nacional del Perú Nº 2012-03319
IMPRESO EN EL PERÚ
PRINTED IN PERU

3. Presentación
Introducirse al estudio de las finanzas requiere de una base fundamental como
lo es las matemáticas financieras. Siendo ésta una de las mejores inversiones
en información que un estudiante puede hacer. ¿Por qué?
Porque el éxito en cualquier organización desde las
pequeñas tiendas de la esquina hasta las grandes
corporaciones multinacionales requiere la comprensión
y el manejo adecuado de cálculos financieros.
Este libro es el resultado de la experiencia docente del
autor con alumnos de las carreras profesionales de
contador público y administración de empresas, así
como con profesionales del mundo de las finanzas.
Con este texto se cubren las necesidades de
ambos colectivos que, aunque diferentes, no son
excluyentes. Teoría y praxis forman un todo y deben
complementarse si se quiere lograr un conocimiento,
lo suficientemente riguroso, para entender y analizar
las operaciones financieras.
El texto contiene, por una parte, los conceptos
teóricos que permiten fundamentar el análisis de
los instrumentos financieros existentes, así como el
diseño de otros nuevos y, por otra parte, con la ayuda
de ejemplos y ejercicios, dichos conceptos se aplican en la
descripción del funcionamiento de las operaciones financieras
más habituales en el mercado.
Por este motivo, el presente texto va dirigido principalmente a empresarios,
estudiantes y profesionales no financieros, que sin tener necesariamente
conocimientos de finanzas, sin embargo, tengan la curiosidad y
deseen conocer los fundamentos de las matemáticas financieras
como herramienta vital de las finanzas corporativas modernas.

5. íNDICE
UNIDAD I
INTRODUCCIÓN A LAS MATEMÁTICAS ACTUARIALES
SESIÓN Nº 1: Conceptos básicos....................................................................................................... 17.
1. Origen de las matemáticas financieras............................................................ 17
1.1. Crédito............................................................................................................................. 17
2. El valor del dinero en el tiempo............................................................................. 18
2.1. Costo de oportunidad.............................................................................................. 19
3. Tasas de interés.................................................................................................................... 22
3.1. Capitalización de interés....................................................................................... 23
4. Monto o valor futuro (S)............................................................................................ 24
5. Interés comercial y real................................................................................................ 25
5.1. ¿Qué tipo de interés se usa o se aplica en la prática?......................... 26
6. Plazo comprendido entre dos fechas................................................................. 26
6.1. Días inicial y final...................................................................................................... 26
6.2. Fecha de vencimiento............................................................................................ 27
7. Horizontes y subhorizontes temporales.......................................................... 29
8. Métodos de afectación al interés y al principal cuando
se reduce el monto............................................................................................................ 30
8.1. PPLI(Primero Principal Luego Interés)........................................................... 30
8.2. PILP(Primero Interés Luego Principal)........................................................... 31
PRÁCTICA DIRIGIDA................................................................................................................. 32
UNIDAD II
LEYES FINANCIERAS EN LA PRÁCTICA
SESIÓN Nº 2: Interés simple................................................................................................................. 37.
1. Introducción.......................................................................................................................... 37
2. Interés con principal y tasa nominal constante....................................... 37
2.1. Calculando el capital inicial o principal (P)................................................ 40
2.2. Calculando la tasa de interés (j)....................................................................... 41
2.3. Calculando el tiempo (n)...................................................................................... 43

6. 3. Interés con principal constante y tasa nominal variable................ 44
4. Monto o valor futuro simple con principal y tasa nominal
variable...................................................................................................................................... 46
5. Monto o valor futuro simple con principal constante y tasa
nominal variable................................................................................................................ 48
6. Valor presente o valor actual simple con principal y tasa
nominal constante............................................................................................................ 50
7. Valor presente o valor actual simple con principal constante
y tasa nominal variable............................................................................................... 52
8. Ecuaciones de valor equivalentes.......................................................................... 54
PRÁCTICA DIRIGIDA................................................................................................................. 58
SESIÓN Nº 3: Interés compuesto....................................................................................................... 63.
1. Introducción.......................................................................................................................... 63
2. Interés con principal y tasa efectiva constante......................................... 63
2.1. Calculando el capital inicial o principal (P)................................................ 65
2.2. Calculando la tasa de interés (i)....................................................................... 67
2.3. Calculando el tiempo (n)...................................................................................... 69
3. Interés con principal constante y tasa efectiva variable.................. 71
4. Monto o valor futuro compuesto con principal y tasa
efectiva constante.............................................................................................................. 73
5. Monto o valor futuro compuesto con principal constante
y tasa efectiva variable................................................................................................. 75
6. Valor presente o valor actual compuesto con principal
y tasa efectiva constante............................................................................................. 77
7. Valor presente o valor actual compuesto con principal
constante y tasa efectiva variable....................................................................... 79
8. Ecuaciones de valor equivalentes.......................................................................... 81
9. Interés compuesto con tasa j capitalizable.................................................... 84
9.1. Valor futuro con tasa j capitalizable............................................................... 87
9.2. Valor presente o valor actual con tasa j capitalizable.......................... 88
PRÁCTICA DIRIGIDA................................................................................................................. 90

7. UNIDAD IIi
OPERACIONES DE DESCUENTO, TASAS, INFLACIÓN Y DEVALUACIÓN Y LAS SEIS LLAVES
MAESTRAS DE LAS MATEMÁTICAS FINANCIERAS
SESIÓN Nº 4: Operaciones de descuento.................................................................................... 97.
1. Introducción.......................................................................................................................... 97
2. Descuento comercial........................................................................................................ 98
2.1. Descuento comercial unitario............................................................................. 98
2.2. Descuento comercial sucesivo o en cadena.............................................. 99
3. Descuento bancario........................................................................................................101
3.1. Descuento bancario simple...............................................................................101
3.2. Descuento bancario compuesto......................................................................105
4. Descuento racional.........................................................................................................109
4.1. Descuento racional simple.................................................................................109
4.2. Descuento racional compuesto.......................................................................114
5. Operaciones de descuento en la práctica......................................................120
PRÁCTICA DIRIGIDA...............................................................................................................123
SESIÓN Nº 5: Tasas....................................................................................................................................129.
1. Introducción........................................................................................................................129
2. Tasa vencida y anticipada..........................................................................................130
3. Tasa nominal proporcional....................................................................................130
4. Conversión de una tasa nominal a efectiva...............................................131
5. Tasa efectiva equivalente............................................................................................133
6. Tasa activa y pasiva.........................................................................................................134
6.1. Tasa de interés pasiva..........................................................................................134
6.2. Tasa de interés activa...........................................................................................135
7. Tasa compensatoria y moratoria.........................................................................136
7.1. Aplicación de tasa compensatoria y moratoria en pagarés...........137
8. TAMN, TAMEX, TIPMN, TIPMEX.......................................................................................138
9. Tasa con capitalización discreta y continua..............................................139
9.1. Tasa con capitalización discreta......................................................................139
9.2. Tasa con capitalización continua....................................................................139
10. Tasa explícita e implícita..............................................................................................140
PRÁCTICA DIRIGIDA...............................................................................................................142

8. SESIÓN Nº 6: Inflación y devaluación.......................................................................................145.
1. Introducción........................................................................................................................145
2. Cálculo de la tasa de inflación.............................................................................146
3. Cálculo de la tasa de interés real.......................................................................149
3.1. Tasa efectiva inflada..............................................................................................150
4. Tipo de cambio.....................................................................................................................151
4.1. Tipo de cambio directo........................................................................................152
4.2. Tipo de cambio cruzado......................................................................................152
5. Tasa de interés en moneda extranjera............................................................153
PRÁCTICA DIRIGIDA...............................................................................................................155
SESIÓN Nº 7: Las seis llaves maestras de las matemáticas financieras........157.
1. Introducción........................................................................................................................157
2. Factor simple de capitalización (FSC).................................................................158
3. Factor simple de actualización (FSA).................................................................159
4. Factor de capitalización de la serie (FCS).......................................................160
5. Factor de depósito al fondo de amortización (FDFA)...........................161
6. Factor de actualización de la serie (FAS).......................................................162
7. Factor de recuperación del capital (FRC).......................................................163
PRÁCTICA DIRIGIDA...............................................................................................................165
UNIDAD Iv
ANUALIDADES Y PROGRAMAS DE AMORTIZACIÓN DE CRÉDITOS
SESIÓN Nº 8: Anualidades vencidas y anticipadas..........................................................171.
1. Introducción........................................................................................................................171
2. Anualidades vencidas u ordinarias..................................................................173
2.1. Valor futuro S de una anualidad vencida..................................................173
2.2. Valor presente P de una anualidad vencida............................................176
3. Anualidades anticipadas............................................................................................180
3.1. Valor futuro S de una anualidad anticipada.............................................180
3.2. Valor presente P de una anualidad anticipada......................................184
PRÁCTICA DIRIGIDA...............................................................................................................188

9. SESIÓN Nº 9: Anualidades diferidas y perpetuas.............................................................191.
1. Introducción........................................................................................................................191
2. Anualidades diferidas...................................................................................................191
2.1. Valor futuro S de una anualidad diferida...................................................192
2.2. Valor presente P de una anualidad diferida............................................193
3. Perpetuidades.......................................................................................................................196
3.1. Valor futuro S de una perpetuidad................................................................196
3.2. Valor presente P de una perpetuidad.........................................................196
PRÁCTICA DIRIGIDA...............................................................................................................199
SESIÓN Nº 10: Programas de amortización de créditos............................................201.
1. Introducción........................................................................................................................201
2. Amortización con interés simple..........................................................................201
2.1. Amortización con interés global.....................................................................202
2.2. Amortización con interés sobre saldos insolutos (al rebatir).........204
3. Amortización con interés compuesto................................................................206
3.1. Sistema de amortización constante (método alemán).....................207
3.2. Sistema de amortización única al vencimiento (método
americano simple).................................................................................................208
3.3. Sistema de pagos constantes (método francés)...................................209
3.4. Sistema de pagos con período de gracia..................................................210
3.5. Sistema de pagos VAC (valor de actualización constante)..............212
4. Costo efectivo del crédito...........................................................................................214
4.1. Uso del VAN y la TIR en la evaluación de crédito.................................215
PRÁCTICA DIRIGIDA...............................................................................................................221
REFERENCIAS BIBLIOGRÁFICAS.............................................................223

11. SUMILLA
El curso pertenece al área de formación
profesional y a la sub-área de finanzas. Propone
capacitar al estudiante en la formulación de
modelos matemáticos básicos para resolver los
problemas financieros. El curso es de naturaleza
teórico-práctica y abarca los siguientes tópicos:
técnica mercantil, interés simple y compuesto,
amortización de préstamos, anualidades o rentas,
seguros de vida y alternativas de inversión.

13. CÓMO ESTUDIAR
LOS MÓDULOS DIDÁCTICOS O TEXTOS AUTOINSTRUCTIVOS
Antes de la lectura
Durante la lectura
Después de la lectura
El método A2D para autodidactas, de Raúl Paredes Mo-
rales, es un método de fácil aplicación para la mayoría
de los estudiantes, inclusive para los no autodidactas. Si
el estudiante aplica este método, su trabajo intelectual
será más rápido y eficaz.
A2D responde a las letras iniciales de los 3 pasos, que
se propone para la lectura de un módulo didáctico o
cualquier otro texto.
Consiste en la exploración preliminar y se debe:
Â
 Echar un vistazo general empezando por el índice, reconociendo
unidades y lecciones que se van explicando en el módulo didáctico.
Â
 Anotar las dudas que van surgiendo durante el vistazo general,
para esclarecerlas durante la lectura o después de ella.
Â
 Adoptar una actitud positiva.
Ésta es la fase más importante del método, el ritmo de lectura lo pone cada
lector. Debes tener presente los siguientes aspectos:
Â
 Mantén una actitud positiva.
Â
 Participa activamente en la lectura: tomando apuntes, subrayando,
resumiendo y esquematizando.
Â
 Si no entiendes lo que lees o encuentras una palabra desconocida,
consulta con tu profesor, tutor o un diccionario.
Esta fase va a afianzar la lectura, mejorando tu comprensión lectora, para
ello debes tener en cuenta lo siguiente:
Â
 Repasa los apuntes tomados durante la lectura.
Â
 Organiza el trabajo y planifica el horario de estudio. Trata de que
sea siempre a la misma hora.
Â
 Realiza los trabajos diariamente. No dejes que se te acumulen las tareas.
Â
 Procura ampliar las lecciones con lecturas complementarias.
Â
 Al final de cada capítulo haz tu cuadro sinóptico o mapa conceptual.
Â
 Elabora tu propio resumen.
Antes de la lectura
Durante la lectura
Después de la lectura
A2D
Enriquece tu vocabulario para entender
mejor las próximas lecturas.
MÉTODO A2D
ORIENTACIONES METODOLÓGICAS

15. INTRODUCCIÓN A LAS MATEMÁTICAS ACTUARIALES
Sesión Nº 1: Conceptos básicos
UNIDAD
I
UNIDAD I

16. COMPETENCIAS
CONCEPTUAL PROCEDIMENTAL ACTITUDINAL
Estudia el origen de las
matemáticas financie-
ras.
Organiza un mapa con-
ceptual de las matemá-
ticas financieras.
Valora la matemática fi-
nanciera como tema de
estudio.

17. Cálculo financiero
P R O E S A D
17
1
Sesión
conceptos básicos
1. ORÍGEN DE LAS MATEMÁTICAS FINANCIERAS
Las matemáticas han sido aplicadas a muchas áreas de las finanzas a través de los años. No
hay mucha información acerca de la historia de las matemáticas financieras, ni de cuál era
el problema que se intentaba solucionar con ellas, lo que yo creo es que se dieron como un
desarrollo involuntario, pero necesario, que complementaba algunas transacciones comerciales o
determinados pagos, por ejemplo los que habían de realizar los aldeanos a sus señores feudales
en la época del feudalismo en Europa. Investigando se encontró que las matemáticas financieras
aparecieron inicialmente con los intereses, creo que «alguien» se dio cuenta que si otro le debía
dinero o vacas o cabras o lo que fuera, él debía recibir una compensación por el tiempo que esta
persona tardara en cancelar la deuda.
Es casi natural considerar que, al igual que otras múltiples actividades que realiza el ser humano,
el comercio, con sus formas y modalidades, que hoy nos parecen asombrosas y alucinantes,
como el mercado de capitales, es el resultado de un proceso, cuyo inicio hay que ubicarlo en
algunos momentos o instituciones del pasado.
El hombre ha logrado satisfacer sus necesidades a través de actividades comerciales diferentes,
siendo el criterio diferenciador el tipo objeto de intercambio empleado por él. En tal sentido, se
identifican las siguientes etapas que fueron apareciendo no necesariamente en orden secuencial:
 Trueque o permuta: se intercambia un bien por otro (ej. papas por arroz).
 Etapa monetaria: aparece el dinero que sirve para efectuar transacciones, y comprar así los
bienes.
 Etapa de crédito: además de mi propio dinero, me endeudo para comprar algún bien.
 Etapa de los documentos o instrumentos financieros: se formalizan más los acuerdos o con-
venios entre los participantes del mercado; se convierten así en instrumentos de vida propia
que son negociados.
De todo lo expuesto anteriormente, podemos señalar que las matemáticas financieras aparecieron
cuando apareció el crédito, a continuación, la definiremos.
1.1. Crédito
Es el traspaso del derecho al uso de un bien por parte de una persona natural o jurídica que
goza de tal derecho y que renuncia a ese uso a favor de otra persona natural o jurídica, la cual lo

18. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
18
adquiere por un plazo determinado o no.
Esta definición de «crédito» abarca cualquier operación de préstamo de cualquier bien, algunas
de tanta envergadura como un crédito en dólares otorgado por el Banco Interamericano de
Desarrollo (BID) a un país latinoamericano o como una concesión por 20 años para explotar
yacimientos mineros en nuestra selva peruana, a la vez que algunas tan simples como el
préstamo de una calculadora entre dos compañeros de curso durante una evaluación.
Ahora, si bien la acepción más conocida de “crédito en dinero” es aquella en la cual una institución
financiera le presta dinero a una persona natural o jurídica, es importante reconocer que este
concepto involucra un conjunto bastante amplio de operaciones, como por ejemplo: depósitos
de ahorro que realizan personas naturales o jurídicas en instituciones financieras (cuentas de
ahorro, depósitos a plazo, depósitos de CTS, etc.), préstamos de carácter comercial (ventas a
plazo) y, entre otros, la inversión en empresas productivas (el inversionista “le presta” dinero a
la empresa).
Esto, sin duda, evidencia que en las operaciones de crédito en dinero el acreedor (la persona que
prestó el dinero) exija al deudor (la persona que recibió el dinero en préstamo) el pago de una
renta por el dinero prestado, renta que recibe el nombre de interés, concepto que veremos con
más detalle más adelante.
2. EL VALOR DEL DINERO EN EL TIEMPO
Para muchas personas resulta discutible el hecho de que se cobren intereses en las operaciones
de crédito en dinero. Incluso, existen determinadas civilizaciones en que ello está penado por la
ley, con base en preceptos religiosos.
A fin de situar este tema en la perspectiva adecuada, evitando las discusiones de carácter ético o
religioso, es importante convencer al lector de que –dada una cierta lógica– resulta difícil discutir
la aplicación de intereses en un préstamo en dinero. Obviamente, otro asunto es la cuantía o
magnitud de tales intereses, a lo cual se hará referencia más adelante.
Supóngase que a usted se le enfrenta al problema de decidir entre dos alternativas mutuamente
excluyentes (puede decidirse por solo una de ellas o por ninguna):
a) Recibir hoy una donación de $10.000.
b) Recibir una donación de $10.000 dentro de 1 año.
No cabe prácticamente ninguna duda que usted preferiría la alternativa (a). Si le preguntasen
los motivos, lo más probable es que usted mencionaría a lo menos uno de los factores que se
mencionan a continuación:
a) La pérdida de poder adquisitivo (debido a la existencia de inflación, con $10.000 disponibles
hoy puedo adquirir más bienes y servicios que con $10.000 dentro de un año).
b) El riesgo (más vale tener $10.000 seguros hoy, que tener una promesa de que recibiré
$10.000 dentro de un año).
c) Los usos alternativos del dinero (con $10.000 colocados a trabajar hoy, podría tener más de
$10.000 dentro de un año).

19. Cálculo financiero
P R O E S A D
19
Alcanzado un cierto acuerdo sobre lo recientemente planteado, cabe preguntarse –entonces–
por qué alguien prestaría $10.000 hoy a 1 año plazo y aceptaría que al vencimiento de ese
plazo le devolviesen los mismos $10.000. Parece evidente que se trata del mismo problema
anteriormente planteado, de tal forma que cualquiera que haya preferido la primera alternativa
de ese problema, no podría ahora defender una postura contraria a la de cobro de intereses.
De esta manera, obviando el problema del riesgo que enfrenta el acreedor al prestar dinero,
el cobro de intereses en las operaciones de crédito en dinero puede ser defendido desde dos
perspectivas: la pérdida de poder adquisitivo del dinero a lo largo del plazo del préstamo (en
una economía con inflación) y la existencia de los llamados «costos de oportunidad» en el uso
del dinero.
El primero de estos factores resulta relativamente obvio, ya que el acreedor a lo menos debiera
considerar que, una vez recuperado el dinero prestado, él pudiera adquirir un conjunto de bienes
equivalente al que podía adquirir con la suma prestada en el momento del préstamo.
El segundo de los factores es más novedoso para las personas que recién se aproximan al tema,
relacionándose con la existencia de alternativas rentables para el uso de una determinada
cantidad de dinero.
2.1. Costo de oportunidad
Es la ganancia o rentabilidad de la mejor alternativa desechada o sacrificada al asignar un bien o
recurso a un uso específico, existiendo usos alternativos rentables para ese mismo bien o recurso.
De acuerdo a ello, el concepto de «costo de oportunidad» es aplicable a cualquier bien o recurso
con usos alternativos y la ganancia o rentabilidad no necesariamente se mide en términos
monetarios.
Así, por ejemplo, el alumno que se encuentra asistiendo a una sesión de cátedra podría determinar
cuál es el costo de oportunidad en que incurre al utilizar su tiempo en esa actividad y tal costo
podría estar medido en términos de una determinada “satisfacción” sacrificada.
No obstante, aquí interesan los costos de oportunidad en el uso de una cantidad de dinero,
medidos en términos de la ganancia o rentabilidad monetaria sacrificada, al realizar una
asignación determinada de esa cantidad de dinero.
Resulta evidente que si bien, en algunos períodos de bajísimas inflación, la pérdida de poder
adquisitivo podría ser considerada no relevante, siempre existirían usos alternativos rentables
para la suma de dinero prestada, de tal forma que el acreedor debiera considerar que el interés
del préstamo fuera suficiente para –a lo menos– compensar el costo de oportunidad en que
incurrió al prestar dinero.
Cabe hacer aquí una breve precisión respecto del caso de las instituciones financieras que
prestan dinero, por cuanto para ellas existe un costo explícito de «captación» del dinero. Estas
instituciones son intermediarias que captan dinero, pagando una renta por ello (tasa de interés
pasiva), con la final de colocar o prestar ese dinero, cobrando a su vez una renta (tasa de
interés activa). A fin de que la institución financiera obtenga una ganancia o «spread» en estas
operaciones, es necesario que la tasa activa supere a la suma de los costos de captación y de
administración directa e indirecta de tales operaciones.

20. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
20
En definitiva, el cobro de intereses en las operaciones de crédito en dinero –en su aceptación
amplia– proviene fundamentalmente de la existencia de costos de oportunidad en el uso del
dinero, los cuales conducen al llamado valor del dinero en el tiempo. Se asigna mayor valor a
$1 disponible hoy que a $1 disponible mañana, porque colocando hoy $1 en una alternativa
rentable es posible tener mañana más de $1.
El valor del dinero en el tiempo conduce a la existencia de matemáticas especiales para cálculos
crediticios, pues se debe reconocer que no siempre es pertinente sumar dos cantidades que
se encuentran ubicadas en distintos momentos en el tiempo, o bien, no es posible saber si es
conveniente por –ejemplo– pagar dos cuotas semestrales de $9.000 o solo una cuota anual de
$20.000 en un determinado crédito.
Ejemplo
El costo de oportunidad
Usted cuenta con las siguientes tres únicas y mutuamente excluyentes1
alternativas para
«invertir» $250.000, a un mes de plazo, todas ellas con el mismo nivel de riesgo:
a) Realizar un depósito en un banco local, que ofrece pagarle a fin de mes un interés de
$2 por cada $100 depositados.
b) Colocar el dinero en una alternativa que reportará un interés de $4.750 al final del
mes.
c) Colocar el dinero en una alternativa que reportará, al final del mes, un interés de $0,25
por cada $100 del depósito previamente reajustado por inflación.
Se pide:
1) Determinar cual sería la mejor alternativa, si se estimase una tasa de inflación men-
sual de 1,6% para el mes relevante.
2) Determinar cual sería la ganancia bruta (en), la tasa de rentabilidad bruta (sobre $)
de cada alternativa y el costo de oportunidad relevante (en $ y en tasa) al seleccionar
cada una de las alternativas. Verificar la respuesta 1).
3) Determinar a partir de cual tasa de inflación (mínima o máxima) se entraría a modificar
la respuesta 1).
Desarrollo:
1. Se calcula cuanto dinero se tendría al final del mes con cada una de las alternativas
a) 250.000 + 250.000 (2/100)
250.000 + 5.000
$255.000
b) 250.000 + 4.750
$254.750
c) Primero se reajustan los $250.000, de acuerdo a la tasa de inflación. Con esta
operación, el deudor le devuelve al acreedor la pérdida de poder adquisitivo que
sufrió durante el período.
1
El término mutuamente excluyente indica que si emprendemos una de las alternativas, entonces no podremos emprender
ninguna de las otras.

21. Cálculo financiero
P R O E S A D
21
250.000 + 250.000(0,016)
250.000 + 4.000
$254.000
Ahora se calculan los intereses sobre los $254.000.
254.000 + 254.000 (0,25/100)
254.000 + 635
$254.635
Por tanto, la mejor alternativa es la alternativa a).
2. Cifras en $ (ganancias)
Cifras en tasa (rentabilidad)
Por lo tanto, resulta evidente que la respuesta 1) es correcta, por cuanto –dado que
todas las alternativas tienen el mismo nivel de riesgo– el evaluador debe elegir
aquella que le otorgue la mayor ganancia o rentabilidad neta positiva, lo que implica
necesariamente restarle a la ganancia o rentabilidad bruta aquella ganancia o
rentabilidad que igualmente se habría obtenido si se hubiera llevado a cabo la mejor
alternativa desechada (costo de oportunidad o tasa de rentabilidad alternativa).
3. En este caso, todas las alternativas cubren la pérdida de poder adquisitivo del período
(250.000) (0,016) = $4.000, con ganancias brutas «después de inflación» de $1.000
la alternativa a), $750, la alternativa b) y $635 la alternativa c), manteniéndose
la primacía de la alternativa a). No obstante, la única alternativa que considera un
reconocimiento explícito de la pérdida de poder adquisitivo es la alternativa c), de
tal forma que a tasas de inflación mayores que 1,6% su ganancia bruta «antes de
inflación» será gradualmente mayor que $4.635, mientras las otras dos alternativas
mantienen inalteradas sus ganancias brutas.
Por calcular, entonces, a qué tasa de inflación mensual f, la ganancia bruta de la
alternativa c) iguala a la de la alternativa a).
[250.000 + 250.000 f ] (1,0025) = 255.000
250.000 (1 + f ) (1,0025) = 255.000
(1 + f ) 250.625 = 255.000
(1 + f ) = 255.000/250.625
f = 1,017456 – 1
f = 0,017456 = 1,75%
Alternativa Ganancia Bruta Costo de Oportunidad Ganancia Neta
a) $5.000 $4.750 $250
b) $4.750 $5.000 –$250
c) $4.635 $5.000 –$365
Alternativa Rentabilidad Bruta Tasa Costo Oportunidad Ganancia Neta
a) 2,00% 1,90% 0,10%
b) 1,90% 2,00% –0,10%
c) 1,85% 2,00% –0,15%

22. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
22
Esto significa que con una tasa de inflación mensual superior a 1,75%, la alternativa c)
superaría a la alternativa a) y pasaría a ser la mejor alternativa. 
3. TASAS DE INTERÉS
La tasa de interés es el precio pagado a los que prestan dinero, mientras que en el caso del capital
social, los inversionistas esperan compensación en la forma de dividendos y capital ganado.
El interés es el alquiler o rédito que se conviene pagar por un dinero tomado como préstamo, la
forma cómo se expresa el precio es la tasa de operación comercial. La unidad de tiempo es el
año. La tasa se expresa en porcentajes (%).
El interés que se paga por una suma de dinero prestado depende de las condiciones contractuales
y varía en razón directa con la cantidad de dinero prestado y con el tiempo de duración del
préstamo. Asimismo, a la oferta monetaria y variables socioeconómicas, etc.
Este concepto, no es nuevo, nuestro Señor Jesucristo lo explicó hace más de dos mil años en una
de sus parábolas. A continuación la citaremos:
“El reino de los cielos es también como un hombre, que al salir de viaje, llamó a sus siervos,
y le confió sus bienes. A uno le dio cinco talentos, a otros dos, y al tercero uno. A cada uno
según su capacidad. Y se fue lejos. El que había recibido cinco talentos, en seguida negoció
con ellos, y ganó otros cinco. Del mismo modo el que había recibido dos, ganó otros dos.
Pero el que había recibido uno, cavó en la tierra, y escondió el dinero de su señor. Después
de mucho tiempo, vino el señor de aquellos siervos, y arregló cuentas con ellos. Llegó el
que había recibido cinco talentos, trajo otros cinco talentos, y dijo: ‘Señor, cinco talentos me
confiaste, aquí tienes otros cinco talentos que gané con ellos’. Su señor le dijo: ‘¡Bien, siervo
bueno y fiel! Sobre poco has sido fiel, sobre mucho te pondré, entra en el gozo de tu Señor’.
Llegó también el que había recibido dos talentos, y dijo ‘Señor, dos talentos me confiaste,
aquí tienes otro dos talentos que gané con ellos’. Su Señor le dijo: ‘¡Bien, siervo bueno y fiel!
Sobre poco has sido fiel, sobre mucho te pondré, entra en el gozo de tu señor’. Llegó también
el que había recibido un talento, y dijo: ‘Señor, sabía que eres hombre duro, que siegas
donde no sembraste, y juntas don de no esparciste, ‘y de miedo, fui y escondí tu talento en
la tierra, aquí tienes lo que es tuyo’. Su Señor respondió: ‘Siervo malo y negligente, sabías
que siego donde no sembré, y junto donde no esparcí. ‘Por eso debías haber dado mi
dinero a los banqueros, y yo hubiera recibido lo mío con el INTERÉS. ‘Quitadle el talento
y dadlo al que tiene diez talentos. ‘Porque al que tiene, le será dado, y tendrá en abundancia,
y al que no tiene, aun lo que tiene, le será quitado. ‘Y al siervo inútil echadlo fuera, en las
tinieblas, allí será el llanto y el crujir de dientes’. SAN MATEO 25:14-30.
De esta manera, la tasa de interés es el porcentaje de variación entre un capital inicial (P) y un
capital final ó monto (S) después de un periodo de tiempo es decir:
i
S P
P
=
− (1)
Pero S – P = I (interés), entonces:
i
I
P
= (2)

23. Cálculo financiero
P R O E S A D
23
Donde:
“ I ” son los intereses que se generan
“ P ” es el capital inicial (en el momento n=0)
“ S ” es el capital final (en el momento n)
“ i ” es la tasa de interés que se aplica
“ n ” es el tiempo que dura la inversión
Ejemplo
Cálculo de la tasa de interés
Si un banco concedió un préstamo de $10.000 y cobro $1.500 de interés después de un
año, ¿cuál fue la tasa del período que el banco aplicó?
Solución:
Los datos son:
i = ?
P = $10.000
I = $1.500
n = 1 año
Reemplazando en la ecuación (2), tenemos:
i = = ≈
$ .
$ .
. %
1 500
10 000
0 15 15
El banco está cobrando una tasa anual del 15%. Actualmente el Banco Central de Reserva
del Perú (BCRP) de acuerdo con su Ley Orgánica D.L. Nº 26123 del 29/12/92, dentro de
sus atribuciones, puede establecer la tasa máxima de interés compensatorio, moratoria y
legal pero solo para las operaciones ajenas al sistema financiero y las operaciones de este
sistema serán determinadas por la libre competencia. 
El interés generado por un principal que se simboliza por la letra I está en función de múltiples
variables, entre las cuales se encuentran:
 La magnitud del principal (capital) colocado o invertido.
 La tasa de interés implícita o explícita.
 El tiempo: a mayor tiempo, mayor interés para un mismo principal y una misma tasa de
interés.
 El riesgo de la operación; se supone que mayor riesgo al principal le corresponde una mayor
tasa de interés que genera un mayor interés.
 Otras variables de carácter económico, político, social, etcétera.
3.1. Capitalización del interés
Si este proceso se da una sola vez durante la vigencia de la cuenta se presenta un régimen de
interés monocapitalizado como el del interés simple; si ocurre múltiples veces, se trata de un

24. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
24
régimen de interés multicapitalizado como el del interés compuesto.
Lo anterior se puede apreciar en la figura 1, así como con un ejemplo sencillo.
Figura 1
Capitalización del interés
Ejemplo
Comparación entre interés simple y compuesto
Supongamos que podemos colocar durante 5 años un capital de $1.000 en dos bancos, el
primero en interés simple y el segundo en interés compuesto, con una tasa del 10% anual
en ambos casos.
En el primer banco, cada año, el capital inicial produciría un interés de 1.000*10%=100.
Así, al acabar el primer año tendríamos $1.100. Al final del segundo año (al no acumularse
el interés) tendríamos $1.200 (el capital sobre el que calculamos el interés permanece
constante $1.000, y al final del tercero $1.300, del cuarto $1.400 y del quinto $1.500.
En el segundo banco el primer año obtendríamos un interés de 1.000*10%=100 y al acabar
el primer año tendríamos $1.100. Para calcular el interés en el segundo año (al acumularse
los intereses) tendríamos 1.100*10%=110, y al final del segundo año tendríamos $1.210.
Al final del tercer año tendríamos $1.331, al final del cuarto $1.464,10 y al final del quinto
$1.610,51.
Como puede observarse en el ejemplo, el interés compuesto produce un mayor capital
final que el interés simple para un mismo capital, duración y tanto.
4. MONTO O VALOR FUTURO (S)
Si se conoce el capital inicial y el interés generado hasta determinado momento, el monto o
valor futuro para ese tiempo se puede calcular con la siguiente fórmula:
S = P + I (3)
INTERÉS
Múltiples
Capitalizaciones
Única
Capitalización
Interés
Simple
Interés
Compuesto

25. Cálculo financiero
P R O E S A D
25
Ejemplo
Cálculo del monto o valor futuro (S)
Si un banco concedió un préstamo de $10.000 y cobro $1.500 después de un año, ¿a
cuánto asciende el monto o valor futuro?
Solución:
Los datos son:
S = ?
P = $10.000
I = $1.500
Reemplazando en la ecuación (3), se tiene:
S = 10.000 + 1.500 = $11.500
El monto o valor futuro asciende a $11.500. 
5. INTERÉS COMERCIAL Y REAL
Cuando el tiempo en un préstamo está dado en días, se vuelve necesario convertir la tasa anual,
semestral, trimestral, cuatrimestral, etc., a una tasa de interés por día. Cuando la tasa anual,
semestral, etc., se convierte a tasa diaria utilizando el año natural (365 días o 366, si el año es
bisiesto2
) como divisor en la fórmula del interés simple o del monto (valor futuro), el interés
obtenido se llama interés real o interés exacto.
Ahora, cuando se lleva la conversión utilizando como divisor el número 360, se dice que se está
utilizando el año comercial. En este caso, el interés obtenido se llama interés comercial o interés
ordinario.
A lo anterior se le conoce como año bancario, el cual se refiere a un período de 360 días. El
año bancario tiene como submúltiplos, entre otros a los semestres, cuatrimestres, trimestres,
bimestres, meses, quincenas y días bancarios, cuyo número de días se indica en la siguiente
tabla:
Período bancario Número de días
Año 360
Semestre 180
Cuatrimestre 120
Trimestre 90
Bimestre 60
Mes 30
Quincena 15
Día 1
2
Un año es bisiesto, cuando el mes febrero cuenta con 29 días. Esto sucede cada cuatro años.

26. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
26
5.1. ¿Qué tipo de interés se usa o se aplica en la práctica?
El año comercial, y por ende el interés comercial, es usado por los bancos, bolsa de valores,
bolsa de comercio, casas comerciales y demás instituciones financieras, debido a que el interés
es mayor que el interés real.
Los bancos acostumbran a calcular los intereses, tomando como base el año de 360 días, pero
para la duración del tiempo de préstamos a plazos menores que un año, cuentan los días efectivos
calendarios.
6. PLAZO COMPRENDIDO ENTRE DOS FECHAS
Desde hace muchos años, con el objeto de facilitar los cálculos, se acostumbra suponer el año de
360 días dividido en 12 meses de 30 días cada uno. Observe que 360 días tiene los siguientes
divisores: 2, 3, 4, 5, 6, 8, 9, 10, 12, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 y 180. Estos divisores
permiten un gran número de simplificaciones, muy útiles cuando se trabaja sin calculadora o
computadora.
Existen varias maneras de medir el tiempo que interviene en el cálculo de los intereses. Es
importante que el lector aplique sus costumbres locales en la solución de los problemas.
6.1. Días inicial y final
Es importante mencionar que para calcular el período de tiempo comprendido entre dos fechas
la primera se excluye y la segunda se incluye; esto porque según la legislación vigente para que
un depósito o inversión genere intereses debe haber permanecido como mínimo un día en la
institución financiera desde la fecha de su deposito como lo demostramos en el siguiente cuadro.
Ejemplo
Número de días: días inicial y final
¿Cuál será el tiempo transcurrido entre el 01 de agosto de 2003 y el 15 de setiembre de
2003?
Solución:
Como puede observarse en el ejemplo, del 01 de agosto al 15 de setiembre de 2003 han
transcurrido 45 días. 
Mes Días Días
transcurridos
Observaciones
Agosto 31 30 Se excluye el 01 de agosto
Setiembre 30 15 Se incluye el 15 de setiembre
Total 45

27. Cálculo financiero
P R O E S A D
27
6.2. Fecha de vencimiento
La fijación de la fecha de vencimiento se establece contractualmente. Por ejemplo, un préstamo
que se recibe el 10 de marzo a 3 meses deberá pagarse el 10 de junio; pero cuando el mismo
préstamo se reciba a 90 días, deberá pagarse el 8 de junio, si la costumbre es contar solo el día
final. Si la fecha final corresponde a un día festivo, la costumbre local indicará si el pago debe
efectuarse el primer día laboral siguiente, sin contar días adicionales para el cobro de intereses.
Para calcular el tiempo transcurrido entre la fecha inicial y la fecha final de períodos mayores
a un año, la costumbre comercial es calcular el tiempo aproximado, computando los años de
360 días y los meses de 30 días. Y para períodos menores de un año, la costumbre comercial es
contar los días calendarios que hay entre dos fechas.
Veamos a continuación cada uno de ellos.
Tiempo aproximado
El número de días comerciales que transcurren, entre dos fechas, puede calcularse considerando
los meses de 30 días y años de 360 días; y restando las fechas.
Ejemplo
Número de días: aproximados
Calcular el número de días aproximados entre el 25 de marzo y el 15 de octubre del mismo
año, utilizando días comerciales y restando las fechas.
Solución:
Considerando días comerciales
En este caso, consideramos los meses de 30 días y el año de 360 días.
Restado las fechas
Si queremos restar las fechas, podemos observar que los meses si se pueden restar
fácilmente pero no lo días, entonces convertimos los meses y los días de tal forma que se
puedan restar. Decimos, 10 meses 15 días equivale a 09 meses 45 días. Recuerde, estamos
considerando los meses de 30 días. Una vez convertido se procede a restar la fechas:
Mes Días
Marzo
Abril
Mayo
Junio
Julio
Agosto
Setiembre
Octubre
5 (30 - 25)
30
30
30
30
30
30
15
Total 200

28. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
28
De esto, 6 meses 20 días, equivale a (=6*30)+20 días) = 200 días. 
Tiempo exacto
El número de días naturales que transcurren entre dos fechas, sin contar una de las dos, puede
calcularse con la tabla de fechas siguiente:
Mes Día
10
03
15
25
Mes Día
09
03
06
45
25
20
Día Ene Feb Mar Abr May Jun Jul Ago Sep Oct Nov Dic Día
1 1 32 60 91 121 152 182 213 244 274 305 335 1
2 2 33 61 92 122 153 183 214 245 275 306 336 2
3 3 34 62 93 123 154 184 215 246 276 307 337 3
4 4 35 63 94 124 155 185 216 247 277 308 338 4
5 5 36 64 95 125 156 186 217 248 278 309 339 5
6 6 37 65 96 126 157 187 218 249 279 310 340 6
7 7 38 66 97 127 158 188 219 250 280 311 341 7
8 8 39 67 98 128 159 189 220 251 281 312 342 8
9 9 40 68 99 129 160 190 221 252 282 313 343 9
10 10 41 69 100 130 161 191 222 253 283 314 344 10
11 11 42 70 101 131 162 192 223 254 284 315 345 11
12 12 43 71 102 132 163 193 224 255 285 316 346 12
13 13 44 72 103 133 164 194 225 256 286 317 347 13
14 14 45 73 104 134 165 195 226 257 287 318 348 14
15 15 46 74 105 135 166 196 227 258 288 319 349 15
16 16 47 75 106 136 167 197 228 259 289 320 350 16
17 17 48 76 107 137 168 198 229 260 290 321 351 17
18 18 49 77 108 138 169 199 230 261 291 322 352 18
19 19 50 78 109 139 170 200 231 262 292 323 353 19
20 20 51 79 110 140 171 201 232 263 293 324 354 20
21 21 52 80 111 141 172 202 233 264 294 325 355 21
22 22 53 81 112 142 173 203 234 265 295 326 356 22
23 23 54 82 113 143 174 204 235 266 296 327 357 23
24 24 55 83 114 144 175 205 236 267 297 328 358 24
25 25 56 84 115 145 176 206 237 268 298 329 359 25
26 26 57 85 116 146 177 207 238 269 299 330 360 26
27 27 58 86 117 147 178 208 239 270 300 331 361 27
28 28 59 87 118 148 179 209 240 271 301 332 362 28
29 29 88 119 149 180 210 241 272 302 333 363 29
30 30 89 120 150 181 211 242 273 303 334 364 30
31 31 90 151 212 243 304 365 31

29. Cálculo financiero
P R O E S A D
29
Mes Días
Marzo
Abril
Mayo
Junio
Julio
Agosto
Setiembre
Octubre
6 (31 - 25)
30
31
30
31
31
30
15
Total 204
Mes Días
15/Octubre
25/Marzo
288
84
Diferencia 204
Para años bisiestos, febrero tiene 29 días y el número de cada día a partir del 1 de marzo, es uno
más que el número dado en la tabla.
Ejemplo
Número de días: exactos
Calcular el número de días naturales entre el 25 de marzo y el 15 de octubre del mismo
año, utilizando días de cada mes y la tabla de fechas.
Solución:
Utilizando los días de cada mes
En este caso, consideramos los meses de acuerdo a los números de días que le corresponden.
Utilizando las tablas de fechas
En este caso, la solución es mucho más sencilla, simplemente nos ubicamos en la tabla de
fecha y buscamos las fechas del problema. Encontramos en ella que para el 15 de octubre
la tabla muestra 288 días y para el 25 de marzo 84 días. Se procede entonces a restar
ambas fechas.
Se puede observar que en ambos casos el resultado es el mismo. Entre el 15 de marzo y
el 15 de octubre hay 204 días exactos.
7. HORIZONTES Y SUBHORIZONTES TEMPORALES
El horizonte temporal de una cuenta es el intervalo de tiempo que existe desde que se abre la
cuenta hasta que se cierra; su plazo se simboliza con la letra n.
n
Apertura de la cuenta Cierre de la cuenta

30. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad I
30
Un subhorizonte temporal es un intervalo de tiempo dentro del horizonte temporal de la cuenta.
Cuando el horizonte temporal se divide en subhorizontes temporales uniformes, su plazo se
simboliza con la letra h. por ejemplo, en un préstamo que debe amortizarse en el plazo de 120
días, con cuotas cada 30 días, el horizonte temporal puede dividirse en cuatro subhorizontes
uniformes; entonces se tiene: n = 120 días y h = 30 días.
n = 120 días
0 h 30 h 60 h 90 h 120
=30 =30 =30 =30
8. MÉTODOS DE AFECTACIÓN AL INTERÉS Y AL PRINCIPAL CUANDO SE REDUCE
EL MONTO
Cuando una deuda se amortiza con un pago, el monto de la misma se reduce en tal cantidad,
pero los importes de sus componentes (interés y capital) pueden reducirse de acuerdo con
diversos métodos.
Por ejemplo, si a las 9:00 a.m. del día de hoy tengo una deuda por $660, compuesto de $600 de
capital y $60 de interés, y durante el transcurso del día y antes de su término se realiza un pago
de $300, entonces el monto se reducirá a $360 ($660 – $300), ¿a qué importes se reducen el
interés y el principal?
La respuesta a esta pregunta depende del método de afectación al interés y al principal cuando
se reduce el monto por elegir: dos de los métodos más usados son los siguientes:
8.1. PPLI (Primero Principal Luego Interés)
Si el importe del pago es menor o igual al principal al inicio del día, se aplica por completo para
reducirlo; de lo contrario, se cancela por completo el principal y la diferencia rebaja el interés.
Este método se usa en interés simple. En el ejemplo dado, si se usa el método PPLI, el pago de
$300 se aplica por completo para rebajar el principal.
Al inicio del día Antes del término del día
Monto Pago Monto
$660 $300 $360
Principal Interés Principal Interés Principal Interés
600 60 ? ? ? ?
Al inicio del día Antes del término del día
Monto Pago Monto
$660 $300 $360
Principal Interés Principal Interés Principal Interés
600 60 300 0 300 0

31. Cálculo financiero
P R O E S A D
31
Al inicio del día Antes del término del día
Monto Pago Monto
$660 $300 $360
Principal Interés Principal Interés Principal Interés
600 60 300 60 300 0
8.2. PILP (Primero Interés Luego Principal)
Si el importe del pago es menor o igual al principal al inicio del día, se aplica por completo para
reducirlo; de lo contrario, se cancela por completo el interés y la diferencia rebaja el principal.
Este método se usa en interés compuesto. En el ejemplo dado, si se usa el método PILP, el pago
se aplica a $60 al interés y $240 al principal.

32. 32
1. Usted deposita en una cuenta del BCP la suma de $4.500 que generó $225 de interés en el
plazo de un mes, ¿cuál fue la tasa de interés de ese período? Rpta. 5% mensual
2. El BWS le concedió un préstamo de $5.000 y cobró $500 de interés después de seis meses,
¿cuál fue la tasa del período que el banco aplicó? Rpta. 10% semestral
3. Usted deposita en una cuenta corriente la suma de $2.000 y lo mantiene durante un trimestre;
la tasa de interés para ese período de tiempo ascendió a 5%. ¿Cuál fue el interés generado
al término del trimestre? Rpta. $100
4. Cierta persona deposita en una cuenta del Interbank la suma de $8.000 y lo mantiene durante
un año; la tasa de interés para ese período de tiempo ascendió a 12%. ¿Cuál fue el interés
generado al término del trimestre? Rpta. $960
5. Usted deposita en una cuenta del BCP la suma de $4.500 y lo mantiene durante un mes. Al
término de dicho plazo usted cuenta con un monto de $4.725. Calcule la tasa de interés que
el banco le pagó. Rpta. 5% mensual
6. Kamila deposita en una cuenta del BCP la suma de $4.500 y lo mantiene durante un mes. Si
el banco paga una tasa de interés del 5%, ¿cuál es el monto actual de la cuenta? Rpta. $4.725
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.

33. 33
7. Calcular el número de días naturales entre el 25 de marzo de 1997 y el 15 de octubre de
1998. Rpta. 569 días
8. Un padre de familia ha depositado en una cuenta de ahorros la suma de $7.500, en el Banco
Bovespa, del día 01 de agosto al 15 de noviembre del año 2002, a una tasa de interés simple
del 45%. Posteriormente ésta disminuyó a 32% a partir del 15 de setiembre, y a partir del 1
de noviembre ésta se incrementó a 36%. ¿Cuántos días transcurre en estos períodos? Rpta.
45 días, 45 días y 14 días
9. Siendo las 9:00 a.m. del día de hoy, tengo una deuda por $1.500, compuesto de $1.250 de
capital y $250 de interés, y durante el transcurso del día y antes de su término se realizó un
pago de $500, ¿a cuánto se reduce el principal y el interés si el acreedor utiliza el método
PPLI? Rpta. $750 principal y $250 interés
10. ¿A cuánto se reduce el principal y el interés si el acreedor utiliza el método PILP? Rpta. $1.000
principal y $0 interés

35. LEYES FINANCIERAS EN LA PRÁCTICA
Sesión Nº 2: Interés simple
Sesión Nº 3: Interés compuesto
UNIDAD
II
UNIDAD II

36. COMPETENCIAS
CONCEPTUAL PROCEDIMENTAL ACTITUDINAL
Identifican las distintas
leyes financieras.
Aplican las leyes finan-
cieras en el desarrollo
de las operaciones fi-
nancieras.
Respetan las opiniones
y los pensamientos de
sus compañeros y pro-
fesores, dentro y fuera
del aula.

37. Cálculo financiero
P R O E S A D
37
2
Sesión
INTERÉS SIMPLE
1. INTRODUCCIÓN
Existen dos modalidades básicas de interés: el interés simple y el interés compuesto, los cuales
difieren en la base sobre la cual se calculan los intereses devengados. En este capítulo, nos
ocuparemos del interés simple.
El interés simple es el importe que produce un capital generado por una tasa de interés nominal
j durante un plazo determinado, en una operación cuya característica fundamental es que dicho
capital permanece constante hasta el vencimiento de la misma. La capitalización, que es la
adición del interés ganado al capital original, se produce únicamente al término de todo el plazo
de la operación.
La capitalización simple es una fórmula financiera que permite calcular el equivalente de un
capital en un momento posterior. Es una ley que se utiliza exclusivamente en el corto plazo
(períodos menores de un año), ya que para períodos más largos se utiliza la “capitalización
compuesta o interés compuesto”, que veremos en el siguiente capítulo.
2. INTERÉS CON PRINCIPAL Y TASA NOMINAL CONSTANTE
Se supone que durante el horizonte temporal de la cuenta a interés simple:
• El principal permanece invariable antes del cierre de la cuenta.
• La tasa de interés nominal j anunciada que se aplica sobre el principal no sufre variaciones.
La fórmula que nos sirve para calcular los intereses que genera un capital es la siguiente:
I = P*j*n (1)
Donde:
“ I ” son los intereses que se generan
“ P ” es el capital inicial o principal (en el momento t=0)
“ j ” es la tasa de interés nominal que se aplica
“ n ” es el tiempo que dura la inversión

38. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
38
La fórmula anterior calcula el interés simple cuando el principal y la tasa de interés nominal no
varían durante el tiempo, cuyo resultado es proporcional al tiempo y al importe del principal; lo
que significa que a mayor plazo de vigencia de la cuenta, se percibe mayor interés.
Al utilizar la fórmula (1), se deben tener en cuenta dos aspectos básicos:
1. La j se debe utilizar en forma decimal, es decir, sin el símbolo de porcentaje (%). Recuerde
que para convertir un porcentaje a forma decimal, éste se divide entre 100.
2. La tasa de interés y el tiempo debe estar expresados en la misma unidad de tiempo. Si la
tasa es anual, el tiempo debe ir en año, si la tasa es mensual, el tiempo irá en meses, etc.
Dado que la tasa de interés nominal puede referirse a diferentes plazos, se designará con las
siguientes siglas:
Tabla 1
Plazos de la tasa de interés nominal
Ejemplo 1
Cálculo del interés (I)
Carlos Portanova solicita un préstamo al BWS por $5.000 a pagar en un año, a una TNA de
30%, ¿qué cantidad deberá pagar por concepto de intereses?
Solución:
Los datos son:
I = ?
P = $5.000
TNA = 30%
n = 1 año
La unidad de tiempo de j y n coincide. Por tanto, reemplazando los valores en la ecuación
(1) se tiene:
I = 5.000 * 0,30 * 1 = $1.500
Carlos pagará al final del plazo $1.500 de interés. 
Tasa nominal Siglas
Anual TNA
Semestral TNS
Cuatrimestral TNC
Trimestral TNT
Bimestral TNB
Mensual TNM
Quincenal TNQ
Diaria TND

39. Cálculo financiero
P R O E S A D
39
Ejemplo 2
Cálculo del interés (I)
Luis Alberto solicita un préstamo al BWS por $10.000 a pagar en cuatro meses, a una TNS
de 18%, ¿qué cantidad deberá pagar por concepto de intereses?
Solución:
Los datos son:
I = ?
P = $10.000
TNS = 18%
n = 4 meses
La unidad de tiempo de j y n no coincide. Por tanto, antes de sustituir es necesario convertir
la TNS a una TNM.
Sustituyendo los valores numéricos en la ecuación (1), se obtiene:
I = 10 000 0 18
4
6
1 200
. * , * $ .
=
Luis Alberto pagará al final del plazo $1.200 de interés. 
Ejemplo 3
Cálculo del interés (I)
¿De qué interés simple podrá disponerse el 27 de noviembre, si el 13 de febrero se invirtió
$2.000 a una TNM del 2%?
Solución:
En este caso, contando los días con la tabla de fechas, encontramos que el número de días
es de 287. Por tanto, sustituyendo los valores numéricos en la ecuación (1), se obtiene:
I = 2 000 0 02
287
30
382 67
. * , * $ ,
=
Se podrá disponer de un interés de $382,67. 
A continuación, veremos algunos ejemplos sobre interés simple, donde se nos pide hallar, ya no
el interés (I), sino el capital inicial (P), la tasa de interés (j) y el tiempo (n).

40. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
40
2.1. Calculando el capital inicial o principal (P)
La fórmula que nos sirve para calcular el capital inicial o principal:
P
I
j n
=
*
(2)
Ejemplo 1
Cálculo del capital inicial (P)
Por un préstamo que se solicitó al BWS a pagar en un año, Carlos Portanova pagó $1.500
de interés, ¿qué cantidad se pidió prestado si el banco aplica una TNA del 30%.
Solución:
Los datos son:
P = ?
TNA = 30%
I = $1.500
n = año
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:
P =
1 500
0 30 1
5 000
.
, *
$ .
=
Carlos pidió prestado la suma de $5.000. 
Ejemplo 2
Cálculo del capital inicial (P)
¿A cuánto asciende un préstamo solicitado por Luis Alberto al BWS a pagar en cuatro meses
a una TNS de 18%, si el banco durante dicho período me cobró un interés de $1.200?
Solución:
Los datos son:
P = ?
TNS = 18%
I = 1.200
n = 4 meses
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:

41. Cálculo financiero
P R O E S A D
41
P =
1 200
0 18
4
6
10 000
.
, *
$ .
=
El préstamo solicitado asciende a $10.000. 
Ejemplo 3
Cálculo del capital inicial (P)
¿A cuánto asciende una inversión que se efectúo el 13 de febrero a una TNM del 2%, si
para el 27 de noviembre había ganado $382,67 de interés?
Solución:
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:
P =
382 67
0 02
287
30
2 000
,
, *
$ .
=
La inversión efectuada el 13 de febrero asciende a $2.000, el mismo que devenga un
interés de $382,67 en 287 días. 
2.2. Calculando la tasa de interés (j)
La fórmula a utilizar para calcular la tasa de interés es la siguiente:
j
I
P n
=
*
(3)
Ejemplo 1
Cálculo de la tasa de interés (j)
Por un préstamo de $5.000 que se solicitó al BWS a pagar en un año, Carlos Portanova
pagó $1.500 de interés, ¿qué TNA aplicó el banco?
Solución:
Los datos son:
j = ?
P = $5.000
I = $1.500
n = 1 año
Sustituyendo los valores numéricos en la ecuación (3), se obtiene:

42. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
42
j
= =
1 500
5 000 1
30
.
. *
%
El banco aplicó una TNA de 30%. ¿Por qué una TNA? Porque en la fórmula n es 1 (anual),
por tanto, j debe ser anual. Recuerde tanto j como n deben estar en la misma unidad de
tiempo. 
Ejemplo 2
Cálculo de la tasa de interés (j)
Luis Alberto solicitó un préstamo al BWS por $10.000 a pagar en cuatro meses. Si el banco
le cobró $1.200 de interés, ¿qué TNS cobró el banco?
Solución:
Los datos son:
j = ?
P = $10.000
I = $1.200
n = 4 meses
Al sustituir los valores numéricos en la ecuación (3), se tiene:
j
= =
1 200
10 000
4
6
18
.
. *
%
El banco aplicó una TNS de 18%. 
Ejemplo 3
Cálculo de la tasa de interés (j)
El 13 de febrero se efectúo una inversión por $2.000. Al 27 de noviembre había ganado
intereses por $382,67, ¿qué TNM obtuvo el inversionista?
Solución:
Sustituyendo los valores numéricos en la ecuación (3), se obtiene:
j
= =
382 67
2 000
287
30
2
,
. *
%
El inversionista obtuvo una TNM de 2%. 

43. Cálculo financiero
P R O E S A D
43
2.3. Calculando el tiempo (n)
La fórmula que nos permite para calcular el tiempo (n) es la siguiente:
n
I
P i
=
*
(4)
Ejemplo 1
Cálculo del tiempo (n)
Carlos Portanova solicita un préstamo al BWS por $5.000 a una TNA de 30%. Si el banco
cobra $1.500 de interés, ¿cuántos años duró la deuda?
Solución:
Los datos son:
n = ?
TNA = 30%
P = $5.000
I = $1.500
Sustituyendo los valores numéricos en la ecuación (4), se obtiene:
n
= =
1 500
5 000 0 30
1
.
. * ,
La deuda tuvo una duración de un año. 
Ejemplo 2
Cálculo del tiempo (n)
Luis Alberto solicitó un préstamo al BWS por $10.000 a una TNS de 18%. Si el banco le
cobró $1.200 de interés, ¿cuántos meses se mantuvo la operación?
Solución:
Los datos son:
n = ?
TNS = 18%
P = $10.000
I = $1.200
Al sustituir los valores numéricos en la ecuación (4), se tiene:

44. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
44
n
= =
1 200
10 000
0 18
6
4
.
. *
,
La operación duró cuatro meses. 
Ejemplo 3
Cálculo del tiempo (n)
El 13 de febrero se efectúo una inversión por $2.000 a una TNM de 2%. Si pasado cierto
tiempo he ganado $382,67 de interés, ¿cuántos días se mantuvo la inversión?
Solución:
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:
n
= =
382 67
2 000
0 02
30
287
,
. *
,
La inversión se mantuvo 287 días. 
3. INTERÉS CON PRINCIPAL CONSTANTE Y TASA NOMINAL VARIABLE
En los ejemplos anteriores se calculo el interés cuando el principal y la tasa nominal son constantes,
pero ¿cómo debe calcularse el interés simple cuando una persona coloca una inversión a un plazo
fijo al cual no pueden efectuársele cargos o abonos luego de la apertura y antes del término del
horizonte temporal, mientras que la tasa de interés está sujeta a las variaciones del mercado?
Cuando en el horizonte temporal de la cuenta el principal no cambia y se produce variaciones
en la magnitud de la tasa de interés nominal, cuyos respectivos plazos pueden cambiar, por
ejemplo de TNA a TNS a TNM, etc. (j tiene un comportamiento variable), el interés simple se
obtiene al modificar de manera conveniente F, de acuerdo con el plazo de j para que n pueda
incluir los plazos de vigencia de las tasas variables durante el horizonte temporal.
La fórmula que calcula el interés generado en un horizonte temporal cuando las tasas o los
períodos de tasa son variables es la siguiente:
I P j
h
F
k
k
k
k
z
= ∗






=
∑
1
(5)
Donde:
“z” es el número de subhorizontes, donde la j no sufre variaciones
“jk” es la tasa nominal anunciada vigente en k-ésimo horizonte
“nk” es el número de periodos de la tasa jk en k-ésimo horizonte
“F” es el plazo de la tasa de interés nominal

45. Cálculo financiero
P R O E S A D
45
Ejemplo 1
Cálculo del interés cuando el principal es constante y la tasa nominal variable
El 13 de febrero se deposita en una cuenta $5.000 bajo un régimen de interés simple. La
TNA vigente al momento del depósito fue de 28%, la misma que bajó a 25% el 09 de julio
y a 22% el 20 de setiembre. La cuenta se cierra el 27 de noviembre. Calcule el interés en
la fecha de cierre.
Solución:
Los datos son:
I = ?
P = $5.000
TNA1
= 28%
TNA2
= 25%
TNA3
= 22%
h1
= 146
h2
= 73
h3
= 68
Según la tabla de fechas, el horizonte temporal total de la operación es de 287 días. Y
dentro de dicho horizonte encontramos tres subhorizontes; el primero de ellos de 146 días;
el segundo de 73 días y el tercero de 68 días.
Reemplazando los valores en la ecuación (5) se tiene:
I = + +





 =
5 000 0 28
146
630
0 25
73
360
0 22
68
360
1 029 03
. * , * , * , * $ . ,
El interés generado asciende a $1.029,03. 
Ejemplo 2
Cálculo del interés cuando el principal es constante y la tasa nominal variable
El 13 de febrero se deposita en una cuenta $5.000, en un banco que paga una tasa de
interés nominal variable. La cuenta se cierra el 27 de noviembre. Al término del plazo se
conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TNA
28,0% 13/02
TNS
12,5% 09/07
TNT
5,5% 20/09
Calcule el interés en la fecha de cierre.

46. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
46
Solución:
Los datos son:
I = ?
P = $5.000
TNA1
= 28%
TNS2
= 12,5%
TNT3
= 5,5%
h1
= 146
h2
= 73
h3
= 68
Este problema es el mismo al ejemplo anterior, en cuanto a horizonte y subhorizontes
temporales. Un horizonte temporal total de 287 días y tres subhorizontes de 146, 73 y 68
días.
Lo que cambia son las tasas nominales, manteniéndose el principal constante.
Reemplazando los valores en la ecuación (5) se tiene:
I = + +





 =
5 000 0 28
146
360
0 125
73
180
0 055
68
90
1 029 03
. * , * , * , * $ . ,
Se puede observar que el resultado es el mismo al del ejemplo anterior. Ante esto surge
una pregunta: ¿cómo puede la operación tener el mismo resultado si las tasas nominales
son variables? La respuesta es que dichas tasas son equivalentes.
Por ejemplo, la TNA de 25% del ejemplo anterior es equivalente a la TNS de 12,5% del
ejemplo actual y la TNA de 22% es equivalente a la TNT de 5,5%.
Para calcular la TNS equivalente de una TNA de 25%, se procede de la siguiente manera:
TNS =
0 25
2
12 5
,
, %
=
Y para calcular la TNT equivalente de una TNA de 22%, se procede de la siguiente manera:
TNS =
0 22
4
5 5
,
, %
=
De lo anteriormente expuesto, se concluye que el interés generado asciende a $1.029,03. 
4.MONTOOVALORFUTUROSIMPLECONPRINCIPALYTASANOMINALVARIABLE
A la suma del capital más el interés simple ganado se le llama monto simple o valor futuro
simple, y se simboliza mediante la letra S. por tanto,
S = P + I (6)

47. Cálculo financiero
P R O E S A D
47
Al sustituir la ecuación (1) en la (5) se obtiene:
S = P + Pjn
Factorizando la expresión anterior se tiene:
S = P[1 + jn] (7)
Las ecuaciones (6) y (7) indican que si un capital se presta o invierte durante un tiempo n, a una
tasa de interés de j% por unidad de tiempo, entonces el capital P se transforma en una cantidad
S al final del tiempo n. Debido a esto, se dice que el dinero tiene un valor que depende del
tiempo. Recuerde un dólar hoy vale más que un dólar mañana.
Ejemplo 1
Cálculo del monto o valor futuro (S)
Carlos Portanova solicita un préstamo al BWS por $5.000 a pagar en un año, a una TNA de
30%, ¿qué monto deberá pagar al final del plazo?
Solución:
Los datos son:
S = ?
P = $5.000
TNA = 30%
n = 1 año
El monto o valor futuro se puede obtener de dos maneras, veamos cada una de ellas:
Método 1
En primer lugar hallamos el interés, el cual es como sigue:
I = 5.000 * 0,30 * 1 = $1.500
Utilizando la ecuación (6) para calcular el valor futuro, se tiene:
S = 5.000 * 0,30 * 1 = $6.500
Método 2
El monto o valor futuro se obtiene directamente utilizando la ecuación (7):
S = 5.000[1 + 0,30 * 1] = $6.500
Carlos pagará al final del plazo un monto de $6.500. 

48. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
48
Ejemplo 2
Cálculo del monto o valor futuro (S)
Luis Alberto solicita un préstamo al BWS por $10.000 a pagar en cuatro meses, a una TNS
de 18%, ¿qué monto deberá pagar al final del plazo?
Solución:
Los datos son:
S = ?
P = $10.000
TNS = 18%
n = 4 meses
Sustituyendo los valores numéricos en la ecuación (7), se obtiene:
S = 10 000 1 0 18
4
6
11 200
. , * $ .
+





 =
Luis Alberto pagará al final del plazo un monto de $11.200. 
Ejemplo 3
Cálculo del monto o valor futuro (S)
¿De qué monto podrá disponerse el 27 de noviembre, si el 13 de febrero se invirtió $2.000
a una TNM del 2%?
Solución:
Sustituyendo los valores numéricos en la ecuación (6), se obtiene:
S = 2 000 1 0 02
287
30
2 382 67
. , * $ . ,
+





 =
Se podrá disponer de un monto de $2.382,67. 
5. MONTO O VALOR FUTURO SIMPLE CON PRINCIPAL CONSTANTE Y TASA
NOMINAL VARIABLE
El monto final cuando se presentan variaciones en la tasa nominal y el principal constante P que
lo produjo puede calcularse con la fórmula siguiente:
S P j
h
F
k
k
k
k
z
= +














=
∑
1
1
* (8)

49. Cálculo financiero
P R O E S A D
49
Ejemplo 1
Cálculo del monto cuando el principal es constante y la tasa nominal variable
El 13 de febrero se deposita en una cuenta $5.000 bajo un régimen de interés simple. La
TNA vigente al momento del depósito fue de 28%, la misma que bajó a 25% el 09 de julio
y a 22% el 20 de setiembre. La cuenta se cierra el 27 de noviembre. Calcule el monto en
la fecha de cierre.
Solución:
Los datos son:
S = ?
P = $
TNA1
= 28%
TNA2
= 25%
TNA3
= 22%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (8) se tiene:
S = + + +





 =
5 000 1 0 28
146
360
0 25
73
360
0 22
68
360
6 029 03
. , * , * , * $ . ,
El monto asciende a $6.029,03. 
Ejemplo 2
Cálculo del monto cuando el principal es constante y la tasa nominal variable
El 13 de febrero se deposita en una cuenta $5.000, en un banco que paga una tasa de
interés nominal variable. La cuenta se cierra el 27 de noviembre. Al término del plazo se
conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TNA 28,0% 13/02
TNS 12,5% 09/07
TNT 5,5% 20/09
Calcule el monto en la fecha de cierre.

50. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
50
Solución:
Los datos son:
S = ?
P = $5.000
TNA1
= 28%
TNS2
= 12,5%
TNT3
= 5,5%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (8) se tiene:
S = + + +





 =
5 000 1 0 28
146
360
0 125
73
180
0 055
68
90
6 029 0
. , * , * , * $ . , 3
3
El monto asciende a $6.029,03. 
6. VALOR PRESENTE O VALOR ACTUAL SIMPLE CON PRINCIPAL Y TASA
NOMINAL CONSTANTE
El siguiente ejemplo servirá para mostrar el significado del concepto de valor presente, llamado
también valor actual.
Suponga que usted, el día de hoy recibe un préstamo de $20.000 a 10 meses de plazo y con una
tasa de interés simple de 2% mensual. El monto a pagar será:
S = 20.000[1 + 0,02 * 10] = $24.000
Por el capital prestado usted deberá pagar $24.000 dentro de 10 meses. $24.000 es el monto
o valor futuro (S) de $20.000. Recíprocamente, se dice que $20.000 es el valor presente o valor
actual (P) de $24.000.
La formula para hallar el valor actual simple, se puede hallar despejando P en la ecuación (7):
P S
jn
=
+






1
1
(9)
Ejemplo 1
Cálculo del valor presente o valor actual (P)
Carlos Portanova solicita un préstamo al BWS a pagar en un año. Si el banco cobra una TNA
de 30% y el monto a pagar al final del plazo asciende a $6.500, ¿qué principal fue lo que
solicitó Carlos al BWS?

51. Cálculo financiero
P R O E S A D
51
Solución:
Los datos son:
P = ?
S = $6.500
TNA = 30%
n = 1 año
Sustituyendo los valores en la ecuación (9), se tiene:
P =
+





 =
6 500
1
1 0 30 1
5 000
.
, *
$ .
Carlos solicitó al BWS la suma de $5.000. 
Ejemplo 2
Cálculo del valor presente o valor actual (P)
Luis Alberto solicita un préstamo al BWS a pagar en cuatro meses. Si el banco cobra una
TNS de 18% y el monto a pagar al final del plazo asciende a $11.200, ¿qué principal fue
solicitado por Luis Alberto al BWS?
Solución:
Los datos son:
P = ?
S = $11.200
TNS = 18%
n = 4 meses
Sustituyendo los valores en la ecuación (9), se tiene:
P =
+












=
11 200
1
1 0 18
4
6
10 000
.
, *
$ .
Luis Alberto pidió prestado la suma $10.000 al BWS.

52. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
52
Ejemplo 3
Cálculo del valor presente o valor actual (P)
¿Qué principal tuvo que ser depositado el 13 de febrero, si fue invertido a una TNM del 2%,
para que el 27 de noviembre tenga un monto de $2.382,67?
Solución:
Sustituyendo los valores numéricos en la ecuación (9), se obtiene:
P =
+












=
2 382 67
1
1 0 02
287
30
2 000
. ,
, *
$ .
El 13 de febrero tuvo que depositarse la suma de $2.000. 
7. VALOR PRESENTE O VALOR ACTUAL SIMPLE CON PRINCIPAL CONSTANTE Y
TASA NOMINAL VARIABLE
El valor presente o valor actual cuando se presentan variaciones en la tasa nominal y el principal
constante P que lo produjo puede calcularse con la fórmula siguiente:
P S
j
h
F
k
k
k
k
z
=
+




















=
∑
1
1
1
*
(10)
Ejemplo 1
Cálculo del valor actual cuando el principal es constante y la tasa nominal variable
El 13 de febrero se efectúa un depósito bajo un régimen de interés simple. La TNA vigente
al momento del depósito fue de 28%, la misma que bajó a 25% el 09 de julio y a 22%
el 20 de setiembre. La cuenta se cierra el 27 de noviembre, la misma que ascendía a un
monto de $6.029,03. Calcule la cantidad que tuvo que depositarse el 13 de febrero.
Solución:
Los datos son:
P = ?
S = $6.029,03
TNA1
= 28%
TNA2
= 25%

53. Cálculo financiero
P R O E S A D
53
TNA3
= 22%
h1
= 146
h1
= 73
h1
= 68
Reemplazando los valores en la ecuación (10) se tiene:
P =
+ + +












6 029 03
1
1 0 28
146
360
0 25
73
360
0 22
68
360
. ,
, * , * , *
=
= $ .
5 000
El 13 de febrero tuvo que depositarse la suma de $5.000. 
Ejemplo 2
Cálculo del valor actual cuando el principal es constante y la tasa nominal variable
El 13 de febrero se abre una cuenta en un banco que paga una tasa de interés nominal
variable. La cuenta se cierra el 27 de noviembre. Al término del plazo el monto de la cuenta
asciende a $6.029,03; asimismo, se conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TNA 28,0% 13/02
TNS 12,5% 09/07
TNT 5,5% 20/09
Calcule la cantidad que fue depositado en el banco.
Solución:
Los datos son:
P = ?
S = $6.029,03
TNA1
= 28%
TNS2
= 12,5%
TNT3
= 5,5%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (10) se tiene:
P =
+ + +











6 029 03
1
1 0 28
146
360
0 125
73
180
0 055
68
90
. ,
, * , * , *


= $ .
5 000
La cantidad que fue depositado en el banco asciende a $5.000. 

54. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
54
8. ECUACIONES DE VALOR EQUIVALENTES
Es usual que deudores y acreedores hagan un convenio para refinanciar sus deudas, es decir
para reemplazar un conjunto de obligaciones que previamente contrajeron por otro conjunto de
obligaciones que le sea equivalente, pero con otras cantidades y fechas.
En las operaciones financieras y mercantiles suelen presentarse situaciones en las cuales deudores
y acreedores –por convenir a sus intereses– se ponen de acuerdo para cambiar las condiciones
pactadas originalmente, lo que genera nuevas relaciones contractuales, como sucede en:
 Refinanciación de deudas.
 Sustitución de varias deudas que vencen en fechas diferentes, por un solo pago.
 Pagos anticipados con relación a una o varias fechas de vencimiento prefijadas.
 Prórrogas de vencimiento de plazos pactados, etcétera.
Para facilitar el planteamiento y resolución de este tipo de situaciones, se utiliza una gráfica
conocida como diagrama de tiempo el cual consiste en una línea recta horizontal en la que
generalmente se anotan las fechas y cantidades originales por un lado y las que las sustituyen,
por el otro lado de la recta. Todas las cantidades que aparecen en el diagrama de tiempo, se
trasladan mediante las fórmulas de interés simple, hasta una fecha común que es conocida como
fecha focal.
En este punto se igualan los valores de la deuda original con los de la nueva estructura de las
obligaciones. Al igualar las dos cantidades se obtendrá la ecuación de valor.
La solución de este tipo de problemas se logra cuando se resuelva la ecuación de valor para
la variable que en ella aparece como incógnita. Esta solución variará un poco de acuerdo a la
ubicación de la fecha focal. Esto es cierto solo en el caso de interés simple. Por tanto, en el
interés simple, las ecuaciones de valor se plantean con una tasa nominal j o tasa de interés
simple y si dos importes son equivalentes en el presente, no necesariamente son equivalentes
en otro momento, como sí ocurre con el interés compuesto.
Ejemplo 1
Ecuaciones de valor equivalentes
Una persona tiene una deuda que debe ser saldada de la siguiente manera: $7.200 en
este momento y $13.400 dentro de dos meses. Si desea pagar completamente su deuda
el día de hoy, ¿cuánto tendrá que pagar, si la TNA es de 24,36%?
Solución:
En primer lugar es necesario establecer la fecha focal, ya que no fue establecido en el
enunciado. Si el deudor desea saldar su deuda el día de hoy, no deberá pagar $20.600 que
es la suma de (7.200 + 13.400), pues los $13.400 son un valor futuro (vencen dentro de
dos meses), mientras que los $7.200 vencen hoy (valor presente). Dos o más cantidades
no se pueden sumar mientras no coincidan, en el tiempo, sus valores de vencimiento. Lo
que se puede hacer es calcular el valor presente de los $13.400 y solo entonces, podríamos
sumarlos con los $7.200. Por tanto, el día de hoy parece una fecha focal “natural” en este
problema; aunque puede elegirse cualquier momento como fecha focal.

55. Cálculo financiero
P R O E S A D
55
El diagrama de tiempo sería el siguiente:
El 0 representa el momento actual o presente y X representa la cantidad total por pagar el
día de hoy para saldar la deuda; esto es, el pago propuesto. La cantidad indica que el valor
futuro de $13.400 se traslada al momento actual, debido a que este punto se ha tomado
como fecha focal. Trasladar un valor futuro al momento actual significa que se obtiene el
valor actual del monto, dos meses antes de su vencimiento. Esto es:
P =
+












=
13 400
1
1 0 2436
60
360
12 877 19
.
, *
$ . ,
Al trasladar el monto (valor futuro) a la fecha focal, todas las cantidades (7.200, 12.877,19
y X) se encuentran, ya en una fecha común en la que es posible su comparación y, por
tanto, se puede plantear la ecuación de valor siguiente:
Valor total de las deudas = Valor total de las deudas
Originales propuestas
Esto es:
7 200 13 400
1
1 0 2436
60
360
. .
, *
+
+












= X
X = $20.077,19
Esta persona tendrá que pagar $20.077,19 el día de hoy y saldar así la deuda.
Anteriormente, se sabía que el resultado depende de la localización de la fecha focal y que
si dos importes son equivalentes en el presente, no necesariamente son equivalentes en
otro momento. Para demostrar esta afirmación, consideremos ahora como fecha focal al
final de los primeros 30 días; esto es, el primer mes.
En este caso se debe obtener el valor futuro de $7.200 por 1 mes; el valor futuro de X por
1 mes; en cambio a los $13.400 le obtenemos su valor presente por 1 mes. La ecuación
de valor sería:
$7.200 $13.400
0 2
meses
Deuda propuesta
Deuda original
x

56. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
56
7 200 1 0 2436
30
360
13 400
1
1 0 2436
30
360
. , * .
, *
+





 +
+













= +






+ = [ ]
=
X
X
X
1 0 2436
30
360
7 346 16 13 133 39 1 0203
20 4
, *
. , . , ,
. 7
79 55
1 0203
20 072 09
,
,
. ,
=
Se observa que en este caso el resultado varía. Esto puede suceder, de hecho sucede,
utilizando interés simple. 
Ejemplo 2
Ecuaciones de valor equivalentes
El día 29 de setiembre la empresa Los Amigos S.A.C., tiene una deuda con el Banco
Santander de $4.000 que vence el 15 de octubre y otra deuda de $5.000 que vence el 15
de noviembre. Los Amigos S.A.C., renegoció con el banco y consolidó sus deudas en una
sola cuenta a interés simple con vencimiento al 30 de diciembre del mismo año, a una
TNA constante de 24%. Se requiere saber el monto que cancelará Los Amigos S.A.C. el 30
de diciembre.
Solución:
En el problema el día 30/12 parece una fecha focal “natural”, aunque puede elegirse
cualquier momento como fecha focal.
Si elegimos como fecha focal el 30/12, entonces la deuda de $4.000 que vence el 15/10
y la deuda de $5.000 que vence el 15/11, la tenemos que trasladar hasta la fecha focal.
Por tanto, se puede plantear la siguiente ecuación de valor:
4 000 1 0 24
76
360
5 000 1 0 24
45
360
9 352
. , * . , *
$ . ,
+





 + +





 =
=
X
X 6
67
Los Amigos S.A.C., tendrá que pagar el 30 de diciembre la suma de $9.352,67. 

57. Cálculo financiero
P R O E S A D
57
Ejemplo 3
Ecuaciones de valor equivalentes
Kamila Romero solicitó en préstamo $4.000 que se registra en una cuenta a interés simple
que genera una TNM de 2% para cancelarlo dentro de 90 días. La señorita Romero se
adelanta al vencimiento del préstamo y amortiza $1.800 el día 25 y $1.000 el día 75,
¿cuánto deberá pagar el día 90 para cancelar su deuda?
Solución:
Como es una operación a interés simple en la que debe haber una sola capitalización,
la ecuación de valor equivalente debe plantearse con la fecha focal ubicada al final del
horizonte temporal (día 90).
Para dar solución al problema, se plantea la ecuación de valor siguiente:
4 000 1 0 02
90
30
1 800 1 0 02
65
30
1 000 1 0 02
. , * . , * . , *
+





 + +





 + +
1
15
30
4240 2 888
1 352





 +
= +
=
X
X
X
.
$ .
Al final de plazo (en el día 90) deberá pagarse el importe de $1.352 para cancelar la
deuda. 

58. 58
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Interés con principal y tasa nominal constante
1. Carito solicita un préstamo al BBVA por $2.500 a pagar en un año, a una TNA de 25%, ¿qué
cantidad deberá pagar por concepto de intereses? Rpta. $625
2. El Universo S.A.C., solicita un préstamo al Interbank por $7.500 a pagar en tres meses, a una
TNC de 10%, ¿qué cantidad deberá pagar por concepto de intereses? Rpta. $562,50
3. ¿De qué interés simple podrá disponerse el 20 de diciembre, si el 30 de marzo se invirtió
$5.000 a una TNT del 5%? Rpta. $736,11
4. Por un préstamo que se solicitó al BBVA a pagar en un año, Carito pagó $625 de interés, ¿qué
cantidad se pidió prestado si el banco aplica una TNA del 25%. Rpta. $2.500
5. ¿A cuánto asciende un préstamo solicitado por El Universo S.A.C. al Interbank a pagar en tres
meses a una TNC de 10%, si el banco durante dicho periodo me cobró un interés de $562,50?
Rpta. $7.500
6. ¿A cuánto asciende una inversión que se efectúo el 30 de marzo a una TNT del 5%, si para el
20 de diciembre se contaba con $736,11 de interés? Rpta. $5.000

59. 59
7. Por un préstamo de $2.500 que se solicitó al BBVA a pagar en un año, Carito pagó $625 de
interés, ¿qué TNA aplicó el banco? Rpta. TNA de 25%
8. El Universo S.A.C. solicitó un préstamo al Interbank por $7.500 a pagar en tres meses. Si el
banco le cobró $562,50 de interés, ¿qué TNC cobró el banco? Rpta. TNC de 10%
9. El 30 de marzo se efectúo una inversión por $5.000. Al 20 de diciembre había ganado
intereses por $736,11, ¿qué TNT obtuvo el inversionista? Rpta. TNT de 5%
10. Carito solicita un préstamo al BBVA por $2.500 a una TNA de 25%. Si el banco nos cobra $625,
¿cuántos años duró la deuda? Rpta. 1 año
11. El Universo S.A.C. solicitó un préstamo al Interbank por $7.500 a una TNC de 10%. Si el banco
le cobró $562,50 de interés, ¿cuántos meses se mantuvo la operación? Rpta. 3 meses
12. El 30 de marzo se efectúo una inversión por $5.000 a una TNT de 5%. Si pasado cierto tiempo
he ganado $736,11 de interés, ¿cuántos días se mantuvo la inversión? Rpta. 265 días
Interés con principal constante y tasa nominal variable
13. El 30 de marzo se deposita en una cuenta $12.000 bajo un régimen de interés simple. La TNS
vigente al momento del depósito fue de 15%, la misma que bajó a 14% el 09 de julio y a
13% el 25 de octubre. La cuenta se cierra el 20 de diciembre, calcule el interés en la fecha
de cierre. Rpta. $2.503,33
14. El 30 de marzo se deposita en una cuenta $12.000, en un banco que paga una tasa de interés
nominal variable. La cuenta se cierra el 20 de diciembre. Al término del plazo se conoce que
las tasas de interés fueron las siguientes:
Tasa A partir del
TNA 30,0% 30/03
TNS 14,0% 09/07
TNT 6,5% 25/10
Calcule el interés en la fecha de cierre. Rpta. $2.503,33
Monto o valor futuro simple con principal y tasa nominal constante
15. Carito solicita un préstamo al BBVA por $2.500 a pagar en un año, a una TNA de 25%, ¿qué
monto deberá pagar al final del plazo? Rpta. $3.125
16. El Universo S.A.C. solicita un préstamo al Interbank por $7.500 a pagar en tres meses, a una
TNC de 10%, ¿qué monto deberá pagar al final del plazo? Rpta. $8.062,50
17. ¿De qué monto podrá disponerse el 20 de diciembre, si el 30 de marzo se invirtió $5.000 a
una TNT del 5%? Rpta. $5.736,11

60. 60
Monto o valor futuro simple con principal constante y tasa nominal variable
18. El 30 de marzo se deposita en una cuenta $12.000 bajo un régimen de interés simple. La
TNS vigente al momento del depósito fue de 15%, la misma que bajó a 14% el 09 de julio y
a 13% el 25 de octubre. La cuenta se cierra el 20 de diciembre, calcule el monto en la fecha
de cierre. Rpta. $14.503,33
19. El 30 de marzo se deposita en una cuenta $12.000, en un banco que paga una tasa de interés
nominal variable. La cuenta se cierra el 20 de diciembre. Al término del plazo se conoce que
las tasas de interés fueron las siguientes:
Tasa A partir del
TNA 30,0% 30/03
TNS 14,0% 09/07
TNT 6,5% 25/10
Calcule el monto en la fecha de cierre. Rpta. $14.503,33
Valor presente o valor actual simple con principal y tasa nominal constante
20. Carito solicita un préstamo al BBVA a pagar en un año. Si el banco cobra una TNA de 25% y
el monto a pagar al final del plazo asciende a $3.125, ¿qué principal solicitó Carito al BBVA?
Rpta. $2.500
21. El Universo S.A.C. solicita un préstamo al Interbank a pagar en tres meses. Si el banco cobra
una TNC de 10% y el monto a pagar al final del plazo asciende a $8.062,50, ¿qué principal
fue solicitado por El Universo S.A.C. al Interbank? Rpta. $7.500
22. ¿Qué principal tuvo que ser depositado el 30 de marzo, si fue invertido a una TNT del 5%,
para que el 20 de diciembre tenga un monto de $5.736,11? Rpta. $5.000
Valor presente o valor actual simple con principal constante y tasa nominal variable
23. El 30 de marzo se efectúa un depósito bajo un régimen de interés simple. La TNS vigente al
momento del depósito fue de 15%, la misma que bajó a 14% el 09 de julio y a 13% el 25
de octubre. La cuenta se cierra el 20 de diciembre, la misma que ascendía a un monto de
$14.503,33. Calcule la cantidad que tuvo que depositarse el 30 de marzo. Rpta. $12.000
24. El 30 de marzo se abre una cuenta en un banco que paga una tasa de interés nominal
variable. La cuenta se cierra el 20 de diciembre. Al término del plazo el monto de la cuenta
asciende a $14.503,33; así mismo, se conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TNA 30,0% 30/03
TNS 14,0% 09/07
TNT 6,5% 25/10
Calcule la cantidad que fue depositado en el banco. Rpta. $12.000

61. 61
Ecuaciones de valor equivalentes
25. Una persona tiene una deuda que debe ser saldada de la siguiente manera: $5.200 en este
momento y $5.200 dentro de dos meses. Si desea pagar su deuda completamente dentro de
30 días, ¿cuánto tendrá que pagar, si la TNA es de 20%? Rpta. $10.401,42
26. Textiles Pacífico S.A.C. tiene una deuda con el BSHC una deuda de $7.500 que vence el 15 de
marzo y otra deuda de $12.500 que vence el 15 de abril. La empresa renegoció con el banco
y consolidó sus deudas en una sola cuenta a interés simple con vencimiento al 25 de abril del
mismo año, a una TNT constante de 5%. Se requiere saber el monto que cancelará Textiles
Pacífico S.A.C. el 25 de abril. Rpta. $20.240,27
27. Verónica Kamila solicitó en préstamo $2.500 que se registra en una cuenta a interés simple
que genera una TNT de 8% para cancelarlo dentro de 90 días. La señorita Verónica se adelanta
al vencimiento del préstamo y amortiza $500 el día 30 y $1.000 el día 70, ¿cuánto deberá
pagar el día 90 para cancelar su deuda? Rpta. $1.155,55

63. Cálculo financiero
P R O E S A D
63
3
Sesión
INTERÉS compuesto
1. INTRODUCCIÓN
El interés es compuesto si, a intervalos de tiempo preestablecidos, el interés vencido es agregado
al capital por lo que también gana intereses. Es decir, los intereses generados en cada período
se integran al capital, y este monto gana intereses al siguiente período.
Su característica fundamental es que el interés generado en cada período de interés se adiciona
al capital anterior, formando un nuevo capital, el mismo que genera un nuevo interés en la
siguiente unidad de tiempo y así sucesivamente durante el plazo pactado, experimentando al
final de cada unidad de tiempo un crecimiento geométrico, a diferencia del interés simple,
donde su crecimiento es lineal o proporcional al tiempo.
2. INTERÉS CON PRINCIPAL Y TASA EFECTIVA CONSTANTE
La fórmula de capitalización compuesta que nos permite calcular los intereses es la siguiente:
I = P[(1 + i)n
- 1] (1)
Donde:
“ i ” es la tasa de interés efectiva que se aplica
La fórmula anterior calcula el interés compuesto cuando el principal y la tasa de interés efectiva
no varían durante el tiempo, cuyo resultado es proporcional al tiempo y al importe del principal;
lo que significa que a mayor plazo de vigencia de la cuenta se percibe mayor interés.
Al utilizar la fórmula (1), se deben tener en cuenta dos aspectos básicos:
1. La i se debe utilizar en forma decimal, es decir, sin el símbolo de porcentaje (%). Recuerde
que para convertir un porcentaje a forma decimal, éste se divide entre 100.
2. La tasa de interés y el tiempo debe estar expresados en la misma unidad de tiempo. Si la
tasa es anual, el tiempo debe ir en año, si la tasa es mensual, el tiempo irá en meses, etc.

64. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
64
Dado que la tasa de interés compuesta o tasa de interés efectiva puede referirse a diferentes
plazos, se designará con las siguientes siglas:
Tabla 1
Plazos de la tasa de interés nominal
Ejemplo 1
Cálculo del interés (I)
El BIF otorgó un préstamo a una empresa local por $10.000 para que lo devuelva en un
año, a una TEA de 25%, ¿qué cantidad deberá pagar por concepto de intereses?
Solución:
Los datos son:
I = ?
P = $10.000
TEA = 25%
n = 1 año
La unidad de tiempo de i y n coincide. Por tanto, reemplazando los valores en la ecuación
(1) se tiene:
I = 10.000[(1+0,25) - 1] = $2.500
Esto significa que la empresa al final del plazo deberá pagar por concepto de intereses la
suma de $2.500. 
Ejemplo 2
Cálculo del interés (I)
Carrusel E.I.R.L., solicita un préstamo al Interbank por $10.000 pagar en cinco meses, a una
TES de 18%, ¿qué cantidad deberá pagar por concepto de intereses?
Tasa nominal Siglas
Anual TEA
Semestral TES
Cuatrimestral TEC
Trimestral TET
Bimestral TEB
Mensual TEM
Quincenal TEQ
Diaria TED

65. Cálculo financiero
P R O E S A D
65
Solución:
Los datos son:
I = ?
P = $10.000
TES = 18%
n = 5 meses
Reemplazando los valores en la ecuación (1) se tiene:
I = +
( ) −





 =
10 000 1 0 28 1 1 478 94
150
180
. , $ . ,
Esto significa que al final del plazo Carrusel E.I.R.L. deberá pagar por concepto de intereses
la suma de $1.478,94. 
Ejemplo 3
Cálculo del interés (I)
¿De qué interés compuesto podrá disponerse el 27 de noviembre, si el 13 de febrero se
invirtió $2.000 a una TEM del 2%?
Solución:
Sustituyendo los valores numéricos en la ecuación (1), se obtiene:
I = +
( ) −





 =
2 000 1 0 02 1 417 16
287
30
. , $ ,
Se podrá disponer de un interés de $417,16. 
A continuación, veremos algunos ejemplos sobre interés compuesto, donde se nos pide hallar, ya
no el interés (I), sino el capital inicial (P), la tasa de interés (i) y el tiempo (n).
2.1. Calculando el capital inicial o principal (P)
La formula que nos sirve para calcular el capital inicial o principal:
P
I
i n
=
+ −
( )
1 1
(2)

66. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
66
Ejemplo 1
Cálculo del capital inicial (P)
Por un préstamo que se solicitó al BIF a pagar en un año, una empresa pagó $2.500 de
interés, ¿qué cantidad se pidió prestado si el banco aplica una TEA del 25%?
Solución:
Los datos son:
P = ?
TEA = 25%
I = $2.500
n = 1 año
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:
P =
+ −
=
2 500
1 0 25 1
10 000
.
( , )
$ .
$10.000 fue lo que se pidió prestado al banco para que al final de un año se pague un
interés de $2.500. 
Ejemplo 2
Cálculo del capital inicial (P)
¿A cuánto asciende un préstamo solicitado por Carrusel E.I.R.L. al Interbank a pagar en
cinco meses a una TES de 18%, si el banco durante dicho período cobra un interés de
$1.478,94?
Solución:
Los datos son:
P = ?
TES = 18%
I = 1.478,94
n = 5 meses
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:
P =
+ −
=
1 478 94
1 0 18 1
10 000
150
180
. ,
( , )
$ .
El préstamo solicitado asciende a $10.000. 

67. Cálculo financiero
P R O E S A D
67
Ejemplo 3
Cálculo del capital inicial (P)
¿A cuánto asciende una inversión que se efectúo el 13 de febrero a una TEM del 2%, si para
el 27 de noviembre se contaba con $417,16 de interés?
Solución:
Sustituyendo los valores numéricos en la ecuación (2), se obtiene:
P =
+ −
=
417 16
1 0 02 1
2 000
278
30
,
( , )
$ .
La inversión efectuada el 13 de febrero asciende a $2.000, el mismo que devenga un
interés de $417,16 en 287 días. 
2.2. Calculando la tasa de interés (i)
La fórmula a utilizar para calcular la tasa de interés es la siguiente:
i
I
P
n
= +





 −
1 1
1/
(3)
Ejemplo 1
Cálculo de la tasa de interés (j)
Por un préstamo de $10.000 que se solicitó al BIF a pagar en un año, una empresa pagó
$2.500 de interés, ¿qué TEA aplicó el banco?
Solución:
Los datos son:
i = ?
P = $10.000
I = $2.500
n = 1 año
Sustituyendo los valores numéricos en la ecuación (3), se obtiene:
i = +





 − =
2 500
10 000
1 1 25
1 1
.
.
%
/
El banco aplicó una TEA de 25%. ¿Por qué una TEA? Porque en la fórmula n es 1 (anual),

68. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
68
por tanto, i debe ser anual. Recuerde tanto i como n deben estar en la misma unidad de
tiempo. 
Ejemplo 2
Cálculo de la tasa de interés (j)
Carrusel de Villa E.I.R.L., solicitó préstamo al Interbank por $10.000 a pagar en cinco meses.
Si el banco le cobró $1.478,94 de interés, ¿qué TES cobró el banco?
Solución:
Los datos son:
i = ?
P = $10.000
I = $1.478,94
n = 5 meses
Al sustituir los valores numéricos en la ecuación (3), se tiene:
i = +





 − =
1 478 94
10 000
1 1 18
1 150 180
. ,
.
%
/( / )
El banco aplicó una TES de 18%. 
Ejemplo 3
Cálculo de la tasa de interés (j)
El 13 de febrero se efectúo una inversión por $2.000. Al 27 de noviembre había ganado
intereses por $417,16, ¿qué TEM obtuvo el inversionista?
Solución:
Sustituyendo los valores numéricos en la ecuación (3), se obtiene:
i = +





 − =
417 16
2 000
1 1 2
1 287 30
,
.
%
/( / )
El inversionista obtuvo una TEM de 2%. 

69. Cálculo financiero
P R O E S A D
69
2.3. Calculando el tiempo (n)
La fórmula que nos permite para calcular el tiempo (n) es la siguiente:
n
I
P
i
=
+






+
( )
log
log
1
1
(4)
Ejemplo 1
Cálculo del tiempo (n)
El BIF otorgó un préstamo a una empresa local por $10.000 para que lo devuelva en un
año, a una TEA de 25%. Si el banco nos cobra $2.500 de interés, ¿cuántos años duró la
deuda?
Solución:
Los datos son:
n = ?
TEA = 25%
P = $10.000
I = $2.500
Sustituyendo los valores numéricos en la ecuación (4), se obtiene:
n =
+






+
( )
=
log
.
.
log ,
2 500
10 000
1
1 0 25
1
La deuda tuvo una duración de un año. 
Ejemplo 2
Cálculo del tiempo (n)
Carrusel E.I.R.L., solicitó un préstamo al Interbank por $10.000 a una TES de 18%. Si el
banco le cobró $1.478,94 de interés, ¿cuántos meses se mantuvo la operación?
Solución:
Los datos son:
n = ?
TES = 18%
P = $10.000
I = $1.478,94

70. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
70
Al sustituir los valores numéricos en la ecuación (4), se tiene:
n =
+






+
( )
=
log
. ,
.
log ,
,
1 478 94
10 000
1
1 0 18
0 8333
Se observa que el resultado es 0,8333 semestres. Esto es así porque la tasa que estamos
usando es semestral y por tanto el resultado es semestral.
Para calcular el número de meses, simplemente multiplicamos 0,8333 x 6, lo que nos da
como resultado 5 meses.
Ahora, si queremos que la fórmula nos arroje el número de meses de manera directa,
entonces la TES tenemos que convertirla primeramente a TEM. El cálculo sería el siguiente:
i = (1 + 0,18)1/6
- 1 = 0,02797
A continuación reemplazamos en la fórmula:
n =
+






+
( )
=
log
. ,
.
log ,
1 478 94
10 000
1
1 0 02797
5
Se puede observar que ambos caso, la operación duró 5 meses. 
Ejemplo 3
Cálculo del tiempo (n)
El 13 de febrero se efectúo una inversión por $2.000 a una TEM de 2%. Si pasado cierto
tiempo he ganado $417,16 de interés, ¿cuántos días se mantuvo la inversión?
Solución:
Sustituyendo los valores numéricos en la ecuación (3), se obtiene:
n =
+






+
( )
=
log
,
.
log ,
,
417 16
2 000
1
1 0 02
9 5667
Se observa que el resultado es 9,5667 meses. Para calcular el número de días, simplemente
multiplicamos 9,5667 x 30, lo que nos da como resultado 287 días.

71. Cálculo financiero
P R O E S A D
71
Ahora, si queremos que la fórmula nos arroje el número de días de manera directa, el
cálculo sería el siguiente:
n =
+






+
( )
=
log
,
.
log ,
417 16
2 000
1
1 0 0006603
278
Se puede observar que ambos caso, la operación duró 287 días. 
3. INTERÉS CON PRINCIPAL CONSTANTE Y TASA EFECTIVA VARIABLE
La fórmula que calcula el interés generado en un horizonte temporal cuando las tasas o los
periodos de tasa son variables es la siguiente:
I P ik
h F
k
z
k k
= +
( ) −






=
∏ 1 1
1
(5)
Ejemplo 1
Cálculo del interés cuando el principal es constante y la tasa efectiva variable
El 13 de febrero se deposita en una cuenta $5.000 bajo un régimen de interés compuesto.
La TEA vigente al momento del depósito fue de 28%, la misma que bajó a 25% el 09 de
julio y a 22% el 20 de setiembre. La cuenta se cierra el 27 de noviembre. Calcule el interés
en la fecha de cierre.
Solución:
Los datos son:
I = ?
P = $5.000
TEA1
= 28%
TEA2
= 25%
TEA3
= 22%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (5) se tiene:
I = +
( ) +
( ) +
( ) −





 =
5 000 1 0 28 1 0 25 1 0 22 1 1
146
360
73
360
68
360
. , , , $ .
. ,
003 62
El interés generado asciende a $1.003,62. 

72. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
72
Ejemplo 2
Cálculo del interés cuando el principal es constante y la tasa efectiva variable
El 13 de febrero se deposita en una cuenta $5.000, en un banco que paga una tasa de
interés efectiva variable. La cuenta se cierra el 27 de noviembre. Al término del plazo se
conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TEA 28,0% 13/02
TES 11,8% 09/07
TET 5,1% 20/09
Calcule el interés en la fecha de cierre.
Solución:
Los datos son:
I = ?
P = $5.000
TEA1
= 28%
TES2
= 11,8%
TET3
= 5,1%
h1
= 146
h2
= 73
h3
= 68
Este problema es el mismo al ejemplo anterior, en cuanto a horizonte y subhorizontes
temporales. Un horizonte temporal total de 287 días y tres subhorizontes de 146, 73 y 68
días.
Lo que cambia son las tasas efectivas, manteniéndose el principal constante.
Reemplazando los valores en la ecuación (5) se tiene:
I = +
( ) +
( ) +
( ) −





 =
5 000 1 0 28 1 0 118 1 0 051 1
146
360
73
180
68
90
. , , , $1
1 003 62
. ,
Se puede observar que el resultado es el mismo al del ejemplo anterior. Ante esto surge
una pregunta: ¿cómo puede la operación tener el mismo resultado si las tasas efectivas
son variables? La respuesta es que dichas tasas son equivalentes.
Por ejemplo, la TEA de 25% del ejemplo anterior es equivalente a la TES de 11,8% del
ejemplo actual y la TEA de 22% es equivalente a la TET de 5,1%.
Para calcular la TES equivalente de una TEA de 25%, se procede de la siguiente manera:
TES = +
( ) − =
1 0 25 1 11 8
2 , , %

73. Cálculo financiero
P R O E S A D
73
Y para calcular la TET equivalente de una TEA de 22%, se procede de la siguiente manera:
TEA = +
( ) − =
1 0 22 1 5 1
4 , , %
De lo anteriormente expuesto, se concluye que el interés generado asciende a $1.003,62. 
4. MONTO O VALOR FUTURO COMPUESTO CON PRINCIPAL Y TASA EFECTIVA
CONSTANTE
Un dólar disponible el día de hoy vale más que un dólar que haya de recibirse el próximo año
porque, si se tiene ahora, usted podría invertirlo, ganar intereses y terminar el próximo año con
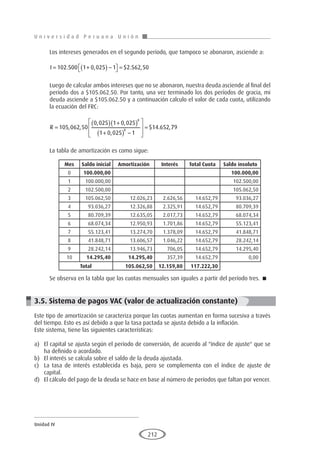
más de un dólar. Esto se puede ver en la figura 1.
Figura 1
Valor futuro compuesto en función del tiempo y diversas tasas de interés
La figura 1 muestra la forma en la que $1 (o cualquier otra suma) crece con el tiempo a varias
tasas de interés. Cuánto más alta sea la tasa de interés, más veloz será la tasa de crecimiento. La
tasa de interés es, de hecho, una tasa de crecimiento; si una suma es depositada y gana un 5%,
entonces los fondos en depósito crecerán a la tasa de 5% por período.
A la suma del capital más el interés compuesto ganado se le llama monto compuesto o valor
futuro compuesto, y se simboliza mediante la letra S. por tanto,
S = P + I (6)
Al sustituir la ecuación (1) en la (6) se obtiene:
S = P + P[(1 + i)n
- 1]
Factor de valor
futuro Tasa del
descuento
8.00
6.00
4.00
2.00
1.00
0.00
0 5 10 15 Tiempo
0%
5%
10%
15%

74. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
74
Factorizando la expresión anterior se tiene:
S = P[(1 + i)n
] (7)
Ejemplo 1
Cálculo del monto o valor futuro (S)
El BIF otorgó un préstamo a una empresa local por $10.000 para que lo devuelva en un
año, a una TEA de 25%, ¿qué monto deberá pagar al final del plazo?
Solución:
Los datos son:
S = ?
P = $10.00
TEA = 25%
n = 1 año
El monto o valor futuro se puede obtener de dos maneras, veamos cada una de ellas:
Método 1
En primer lugar hallamos el interés, el cual es como sigue:
I = 10.000[(1+ 0,25) - 1] = $2.500
Utilizando la ecuación (6) para calcular el valor futuro, se tiene:
S = 10.000 + 2.500 = $12.500
Método 2
El monto o valor futuro se obtiene directamente utilizando la ecuación (7):
S = 10.000[(1 + 0,25)] = $12.500
La empresa pagará al final del plazo un monto de $12.500. 
Ejemplo 2
Cálculo del monto o valor futuro (S)
Carrusel E.I.R.L., solicita un préstamo al Interbank por $10.000 pagar en cinco meses, a una
TES de 18%, ¿qué monto deberá pagar al final del plazo?

75. Cálculo financiero
P R O E S A D
75
Solución:
Los datos son:
S = ?
P = $10.000
TES = 18%
n = 5 meses
Reemplazando los valores en la ecuación (7) se tiene:
S= +
( )





 =
10 000 1 0 18 11 478 94
150
180
. , $ . ,
Esto significa que al final del plazo la empresa deberá pagar un monto de $11.478,94. 
Ejemplo 3
Cálculo del monto o valor futuro (S)
¿De qué monto compuesto podrá disponerse el 27 de noviembre, si el 13 de febrero se
invirtió $2.000 a una TEM del 2%?
Solución:
Sustituyendo los valores numéricos en la ecuación (1), se obtiene:
S= +
( )





 =
2 000 1 0 02 2 417 16
287
30
. , $ . ,
Se podrá disponer de un monto de $2.417,16. 
5. MONTO O VALOR FUTURO COMPUESTO CON PRINCIPAL CONSTANTE Y
TASA EFECTIVA VARIABLE
El monto final cuando se presentan variaciones en la tasa efectiva y el principal constante P que
lo produjo puede calcularse con la fórmula siguiente:
S P ik
h F
k
z
k k
= +
( )






=
∏ 1
1
(8)
Ejemplo 1
Cálculo del monto cuando el principal es constante y la tasa efectiva variable
El 13 de febrero se deposita en una cuenta $5.000 bajo un régimen de interés compuesto.

76. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
76
La TEA vigente al momento del depósito fue de 28%, la misma que bajó a 25% el 09 de
julio y a 22% el 20 de setiembre. La cuenta se cierra el 27 de noviembre. Calcule el monto
en la fecha de cierre.
Solución:
Los datos son:
S = ?
P = $5.000
TEA1
= 28%
TEA2
= 25%
TEA3
= 22%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (8) se tiene:
S = +
( ) +
( ) +
( )





 =
5 000 1 0 28 1 0 25 1 0 22 6 0
146
360
73
360
68
360
. , , , $ . 0
03 62
,
El monto asciende a $6.003,62. 
Ejemplo 2
Cálculo del monto cuando el principal es constante y la tasa efectiva variable
El 13 de febrero se deposita en una cuenta $5.000, en un banco que paga una tasa de
interés efectiva variable. La cuenta se cierra el 27 de noviembre. Al término del plazo se
conoce que las tasas de interés fueron:
Tasa A partir del
TEA 28,0% 13/02
TES 11,8% 09/07
TET 5,1% 20/09
Calcule el monto en la fecha de cierre.
Solución:
Los datos son:
S = ?
P = $5.000
TEA1
= 28%
TES2
= 11,8%
TET3
= 5,1%

77. Cálculo financiero
P R O E S A D
77
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (8) se tiene:
S = +
( ) +
( ) +
( )





 =
5 000 1 0 28 1 0 118 1 0 051 6
146
360
73
180
68
90
. , , , $ .0
003 62
,
El monto asciende a $6.003,62. 
6. VALOR PRESENTE O VALOR ACTUAL COMPUESTO CON PRINCIPAL Y TASA
EFECTIVA CONSTANTE
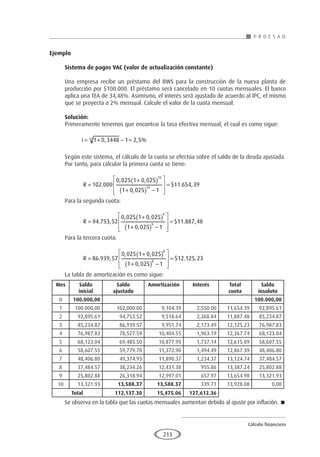
El siguiente ejemplo servirá para mostrar el significado del concepto de valor presente, llamado
también valor actual. (Ver figura 2)
Figura 2
Valor actual compuesto en función del tiempo y diversas tasas de interés
Suponga que usted, el día de hoy recibe un préstamo de $20,000 a 10 meses de plazo y con una
tasa de interés compuesta de 2% mensual. El monto a pagar será:
S = $20.000[(1 + 0,02)10
] = $4.379,89
Por el capital prestado usted deberá pagar $24.379,89 dentro de 10 meses. $24.379,89 es el
monto o valor futuro (S) de $20.000. Recíprocamente, se dice que $20.000 es el valor presente
o valor actual (P) de $24.379,89. Esto significa que $20.000 hoy es equivalente a $24.379,89
dentro de 10 meses a una tasa de interés compuesta del 2% mensual.
Factor de valor
futuro
Tasa del
descuento
0.80
0.60
0.40
0.20
0.00
0 5 10 15
Tiempo
15%
10%
5%

78. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
78
La figura 2 muestra que el valor presente de una suma que haya de recibirse en alguna fecha
futura disminuye (1) a medida que la fecha de pago se extiende más hacia el futuro y (2) a
medida que aumenta la tasa de descuento.
La fórmula para hallar el valor actual compuesto, se puede hallar despejando P en la ecuación
(7):
P S
i
n
=
+
( )








1
1
(9)
Ejemplo 1
Cálculo del valor presente o valor actual (P)
Una empresa local solicitó un préstamo al BIF a pagar en un año. Si el banco cobra una
TEA de 25% y el monto a pagar al final del plazo asciende a $12.500, ¿qué principal fue lo
solicitó dicha empresa?
Solución:
Los datos son:
P = ?
S = $12.500
TEA = 25%
n = 1 año
Sustituyendo los valores en la ecuación (9), se tiene:
P =
+
( )








12 500
1
1 0 25
.
,
La empresa solicitó al BIF la suma de $10.000. 
Ejemplo 2
Cálculo del valor presente o valor actual (P)
Carrusel E.I.R.L. solicita un préstamo al Interbank pagar en cinco meses. Si el banco cobra
una TES de 18% y el monto a pagar al final del plazo asciende a $11.478,94, ¿qué principal
fue solicitado por Carrusel E.I.R.L. al Interbank?
Solución:
Los datos son:

79. Cálculo financiero
P R O E S A D
79
P = ?
S = $11.478,94
TES = 18%
n = 5 meses
Reemplazando los valores en la ecuación (9) se tiene:
P =
+
( )










=
11 478 94
1
1 0 18
10 000
150
180
. ,
,
$ .
Carrusel E.I.R.L. solicitó al Interbank la suma de $10.000. 
Ejemplo 3
Cálculo del valor presente o valor actual (P)
¿Qué principal tuvo que ser depositado el 13 de febrero, si fue invertido a una TEM del 2%,
para que el 27 de noviembre tenga un monto de $2.417,16?
Solución:
Sustituyendo los valores numéricos en la ecuación (9), se obtiene:
P =
+
( )










=
2 417 16
1
1 0 02
2 000
287
30
. ,
,
$ .
El 13 de febrero tuvo que depositarse la suma de $2.000. 
7. VALOR PRESENTE O VALOR ACTUAL COMPUESTO CON PRINCIPAL
CONSTANTE Y TASA EFECTIVA VARIABLE
El valor presente o valor actual cuando se presentan variaciones en la tasa efectiva y el principal
constante P que lo produjo puede calcularse con la fórmula siguiente:
P S
ik
h F
k
z
k k
=
+
( )












=
∏
1
1
1
(10)

80. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
80
Ejemplo 1
Cálculo del valor presente o valor actual cuando el principal es constante y la tasa
efectiva variable
El 13 de febrero se efectúa un depósito bajo un régimen de interés compuesto. La TEA
vigente al momento del depósito fue de 28%, la misma que bajó a 25% el 09 de julio y a
22% el 20 de setiembre. La cuenta se cierra el 27 de noviembre, la misma que ascendía
a un monto de $6.003,62. Calcule la cantidad que tuvo que depositarse el 13 de febrero.
Solución:
Los datos son:
P = ?
S = $6.003,62
TEA1
= 28%
TEA2
= 25%
TEA3
= 22%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (10) se tiene:
P =
+
( ) +
( ) +
( )







6 003 62
1
1 0 28 1 0 25 1 0 22
146
360
73
360
68
360
. ,
, , ,




= $ .
5 000
El 13 de febrero tuvo que depositarse la suma de $5.000. 
Ejemplo 2
Cálculo del valor presente o valor actual cuando el principal es constante y la tasa
efectiva variable
El 13 de febrero se abre una cuenta en un banco que paga una tasa de interés efectiva
variable. La cuenta se cierra el 27 de noviembre. Al término del plazo el monto de la cuenta
asciende a $6.003,62; así mismo, se conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TEA 28,0% 13/02
TES 11,8% 09/07
TET 5,1% 20/09
Calcule la cantidad que fue depositado en el banco.

81. Cálculo financiero
P R O E S A D
81
Solución:
Los datos son:
P = ?
S = $6.003,62
TEA1
= 28%
TES2
= 11,8%
TET3
= 5,1%
h1
= 146
h2
= 73
h3
= 68
Reemplazando los valores en la ecuación (10) se tiene:
P =
+
( ) +
( ) +
( )






6 003 62
1
1 0 28 1 0 118 1 0 051
146
360
73
180
68
90
. ,
, , , 




= $ .
5 000
La cantidad que fue depositado en el banco asciende a $5.000. 
8. ECUACIONES DE VALOR EQUIVALENTES
Ya se vio, en el capítulo anterior, que una ecuación de valor es una igualdad que establece
que la suma de los valores de un conjunto de deudas es igual a la suma de los valores de un
conjunto de deudas propuesto para reemplazar al conjunto original, una vez que sus valores de
vencimiento han sido trasladados a una fecha arbitrariamente elegida, llamada fecha focal.
Como se vio, al estudiar las ecuaciones de valor a interés simple, observamos que los resultados
varían al cambiar la fecha focal, en un mismo problema. En las ecuaciones de valor a interés
compuesto, el resultado no se altera al tomar distintas fechas; por tanto, puede seleccionarse
cualquier fecha para llevar a cabo la igualdad de las obligaciones, siendo el resultado siempre
el mismo.
Las ecuaciones de valor a interés compuesto son una de las técnicas más útiles de la matemática
financiera para la resolución de diversos problemas financieros.
Ejemplo 1
Ecuaciones de valor equivalentes
Una persona tiene una deuda que debe ser saldada de la siguiente manera: $7.200 en
este momento y $13.400 dentro de dos meses. Si desea pagar completamente su deuda
el día de hoy, ¿cuánto tendrá que pagar, si la TEA es de 24,36%?
Solución:
Como se mencionó en el capítulo anterior, si el deudor desea saldar su deuda el día de

82. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
82
hoy, no deberá pagar $20.600 que es la suma de (7.200 + 13.400), pues los $13.400
son un valor futuro (vencen dentro de dos meses), mientras que los $7.200 vencen hoy
(valor presente). Dos o más cantidades no se pueden sumar mientras no coincidan en el
tiempo sus valores de vencimiento. Lo que se puede hacer es calcular el valor presente
de los $13.400 y solo entonces, podríamos sumarlos con los $7.200. Por tanto, el día de
hoy parece una fecha focal “natural” en este problema; aunque puede elegirse cualquier
momento como fecha focal y el resultado sería el mismo.
El diagrama de tiempo sería el siguiente:
El 0 representa el momento actual o presente y X representa la cantidad total por pagar el
día de hoy para saldar la deuda; esto es, el pago propuesto. La cantidad indica que el valor
futuro de $13.400 se traslada al momento actual, debido a que este punto se ha tomado
como fecha focal. Trasladar un valor futuro al momento actual significa que se obtiene el
valor actual del monto, dos meses antes de su vencimiento. Esto es:
P =
+
( )








=
13 400
1
1 0 2436
12 921 85
60 360
.
,
$ . ,
/
Al trasladar el monto (valor futuro) a la fecha focal, todas las cantidades (7.200, 12.921,85
y X) se encuentran, ya en una fecha común en la que es posible su comparación y, por
tanto, se puede plantear la ecuación de valor siguiente:
Valor total de las deudas = Valor total de las deudas
Originales propuestas
Esto es:
7 200 13 400
1
1 0 2436
20 121 85
60 360
. .
,
$ . ,
/
+
+
( )








=
=
X
X
Esta persona tendrá que pagar $20.121,85 el día de hoy y saldar así la deuda.
Deuda original
Deuda propuesta
$7.200 $13.400
0
X
2
meses

83. Cálculo financiero
P R O E S A D
83
Anteriormente, se mencionó que el resultado no depende de la localización de la fecha
focal. Para demostrar esta afirmación, consideremos ahora, como fecha focal el momento
en que vence los $13.400; esto es, el segundo mes.
En este caso se debe obtener el valor futuro de $7.200 por 2 meses; el valor futuro de X
por 2 meses; en cambio los $13.400 permanece inalterado, puesto que se encuentra en la
fecha focal. La ecuación de valor sería:
7 200 1 0 2436 13 400 1 0 2436
7
60
360
60
360
. , . ,
.
+
( )





 + = +
( )






X
4
466 42 13 400 1 037
20 866 42
1 037
20 121 85
, , ,
. ,
,
. ,
+ = [ ]
= =
X
X
Se observa que el resultado es el mismo en ambos casos. 
Ejemplo 2
Ecuaciones de valor equivalentes
El día 29 de setiembre la empresa Los Amigos S.A.C., tiene una deuda con el Banco
Santander una deuda de $4.000 que vence el 15 de octubre y otra deuda de $5.000 que
vence el 15 de noviembre. La empresa renegoció con el banco y consolidó sus deudas en
una sola cuenta a interés compuesto con vencimiento al 30 de diciembre del mismo año,
a una TEA constante de 24%. Se requiere saber el monto que cancelará Los Amigos S.A.C.
el 30 de diciembre.
Solución:
En el problema el día 30/12 parece una fecha focal “natural”, aunque puede elegirse
cualquier momento como fecha focal.
Si elegimos como fecha focal el 30/12, entonces la deuda de $4.000 que vence el 15/10
y la deuda de $5.000 que vence el 15/11, la tenemos que trasladar hasta la fecha focal.
Por tanto, se puede plantear la siguiente ecuación de valor:
4 000 1 0 24 5 000 1 0 24
9 29
76
360
45
360
. , . ,
$ .
+
( )





 + +
( )





 =
=
X
X 5
5 11
,
Los Amigos S.A.C., tendrá que pagar el 30 de diciembre la suma de $9.295,11. 

84. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
84
Ejemplo 3
Ecuaciones de valor equivalentes
Kamila Romero solicitó en préstamo $4.000 que se registra en una cuenta a interés
compuesto que genera una TEM de 2% para cancelarlo dentro de 90 días. La señorita
Romero se adelanta al vencimiento del préstamo y amortiza $1.800 el día 25 y $1.000 el
día 75, ¿cuánto deberá pagar el día 90 para cancelar su deuda?
Solución:
Para dar solución al problema, se plantea la ecuación de valor siguiente:
4 000 1 0 02 1 800 1 0 02 1 000 1 0 0
90
30
65
30
. , . . . ,
+
( )





 = +
( )





 + + 2
2
4 244 83 2 888 86
1 355 97
15
30
( )





 +
= +
=
X
X
X
. , . ,
$ . ,
Al final del plazo (en el día 90) deberá pagarse el importe de $1.355,97 para cancelar la
deuda. 
9. INTERÉS COMPUESTO CON TASA J CAPITALIZABLE
El interés compuesto también puede ser generado por una tasa nominal j capitalizable m veces
(m es el número de períodos que capitaliza la tasa nominal en su respectivo plazo).
El período convenido para convertir el interés en capital se llama período de capitalización o
período de conversión. El número de veces por año en los que los intereses se capitalizan, se
llama frecuencia de capitalización.
Si el período de capitalización de intereses es, digamos mensual, entonces las expresiones
siguientes son equivalentes:
“el interés es capitalizable mensualmente”,
“es convertible mensualmente”,
“es compuesto mensualmente”,
“es interés nominal mensual” o
“compuesto por mes”.
Todos significan que cada mes los intereses se capitalizan o se integran al capital, es decir, se
suma al capital al término de cada mes.
Al dar la tasa de interés en un problema de interés compuesto se menciona enseguida el periodo
de capitalización.
Por ejemplo:

85. Cálculo financiero
P R O E S A D
85
38% anual capitalizable cada semestre
40% capitalizable mensualmente3
2.55% mensual capitalizable cada mes
10.2% trimestral con capitalización quincenal
25% convertible cada mes4
A continuación se ha elaborado la tabla 2 que muestra las frecuencias de capitalización más
comunes.
Tabla 2
Intereses y frecuencia de capitalización
Si los intereses se capitalizan cada → La frecuencia de capitalización es
Año 1
Semestre 2
Cuatrimestre 3
Trimestre 4
Mes 12
Quincena 24
Día 360
En la práctica, las tasas pasivas son expresadas en términos nominales con una frecuencia de
capitalización determinada, de acuerdo con el tipo de operación realizada. Los ahorros capitalizan
mensualmente y los depósitos a plazo capitalizan a diario.
La fórmula de capitalización compuesta que nos permite calcular los intereses es la siguiente:
I P
j
m
n m
= +





 −








1 1
*
(11)
Donde:
“ j ” es la tasa de interés nominal
“ m ” es la frecuencia de capitalización
Ejemplo 1
Interés con capitalización mensual
Kamila Romero deposita en una cuenta de ahorros del BWS la suma de $5.000. Calcule los
intereses que obtendrá Kamila después de un año si el banco aplica una TNA de 12% con
capitalización mensual.
3
Se entiende que se trata de una tasa de interés anual, con capitalización de intereses en forma mensual.
4
Ésta es otra forma de indicar la capitalización de los intereses. El 25% es anual y los intereses se capitalizan cada mes o
mensualmente.

86. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
86
Solución:
Los datos son:
I = ?
P = $5.000
i = 12%
n = 1 año
Sustituyendo los valores en la ecuación (11), se obtiene:
I = +





 −








=
5 000 1
0 12
12
1 634 13
1 12
.
,
$ ,
*
Al final del plazo Kamila obtendrá $634,13 de intereses. 
Ejemplo 2
Interés con capitalización diario
Kamila Romero deposita en una cuenta a plazo fijo del BWS la suma de $5.000. Calcule los
intereses que obtendrá Kamila después de un año si el banco aplica una TNA de 12% con
capitalización diaria.
Solución:
Los datos son:
I = ?
P = $5.000
i = 12%
n = 1 año
Sustituyendo los valores en la ecuación (11), se obtiene:
I = +





 −








=
5 000 1
0 12
360
1 637 37
1 360
.
,
$ ,
*
Al final del plazo Kamila obtendrá $637,37 de intereses. 
Como hemos observado en los ejemplos anteriores (1 y 2), los intereses son mayores cuando,
en un año, la TNA se capitaliza muchas más veces durante el mismo. Veamos, un resumen, de
esto en la tabla 3.

87. Cálculo financiero
P R O E S A D
87
Tabla 3
Comparación de una inversión a una TNA de 12% con diferentes períodos de capitalización
Período de
Inversión TNA Capitalización m Intereses
$5.000 12% Anual 1 $600,00
$5.000 12% Semestral 2 $618,00
$5.000 12% Cuatrimestral 3 $624,32
$5.000 12% Trimestral 4 $627,54
$5.000 12% Mensual 12 $634,13
$5.000 12% Quincenal 24 $635,80
$5.000 12% Diario 360 $637,37
9.1. Valor futuro con tasa j capitalizable
La fórmula que nos permite calcular el valor futuro con una tasa j capitalizable es la siguiente:
S P
j
m
n m
= +














1
*
(12)
Ejemplo 1
Valor futuro con capitalización mensual
Kamila Romero deposita en una cuenta de ahorros del BWS la suma de $5.000. Calcule el
monto que obtendrá Kamila después de un año, si el banco aplica una TNA de 12% con
capitalización mensual.
Solución:
Los datos son:
S = ?
P = $5.000
i = 12%
n = 1 año
m = 12
Sustituyendo los valores en la ecuación (12), se obtiene:
S = +














=
5 000 1
0 12
12
5 634 13
1 12
.
,
$ . ,
*
Al final del plazo Kamila obtendrá un monto de $5.634,13. 

88. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad II
88
Ejemplo 2
Valor futuro con capitalización diario
Kamila Romero deposita en una cuenta a plazo fijo del BWS la suma de $5.000. Calcule el
monto que obtendrá Kamila después de un año, si el banco aplica una TNA de 12% con
capitalización diaria.
Solución:
Los datos son:
S = ?
P = $5.000
i = 12%
n = 1 año
m = 360
Sustituyendo los valores en la ecuación (12), se obtiene:
S = +














=
5 000 1
0 12
360
5 637 37
1 360
.
,
$ . ,
*
Al final del plazo Kamila obtendrá un monto de $5.637,37. 
9.2. Valor presente o valor actual con tasa j capitalizable
La fórmula que nos permite calcular el valor futuro con una tasa j capitalizable es la siguiente:
P S
j
m
n m
=
+




















1
1
* (13)
Ejemplo 1
Valor actual con capitalización mensual
Kamila Romero depositó en una cuenta de ahorros del BWS durante un año. Si el banco
aplicó una TNA de 12% con capitalización mensual y el monto obtenido al final del plazo
asciende a $5.634,13. Calcule el principal que depositó Kamila hace un año.
Solución:
Los datos son:

89. Cálculo financiero
P R O E S A D
89
P = ?
S = $5.634,13
i = 12%
n = 1 año
m = 12
Sustituyendo los valores en la ecuación (13), se obtiene:
P =
+




















=
5 634 13
1
1
0 12
12
5 000
1 12
. ,
,
$ .
*
Kamila depositó hace un año un capital de $5.000. 
Ejemplo 2
Valor actual con capitalización diaria
Kamila Romero depositó en una cuenta de ahorros del BWS durante un año. Si el banco
aplicó una TNA de 12% con capitalización diaria y el monto obtenido al final del plazo
asciende a $5.637,37. Calcule el principal que depositó Kamila hace un año.
Solución:
Los datos son:
P = ?
S = $5.637,37
i = 12%
n = 1 año
m = 360
Sustituyendo los valores en la ecuación (13), se obtiene:
P =
+




















=
5 637 37
1
1
0 12
360
5 000
1 360
. ,
,
$ .
*
Kamila depositó hace un año un capital de $5.000. 

90. 90
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Interés con principal y tasa efectiva constante
1. Carito solicita un préstamo al BBVA por $2.500 a pagar en un año, a una TEA de 25%, ¿qué
cantidad deberá pagar por concepto de intereses? Rpta. $625
2. El Universo S.A.C., solicita un préstamo al Interbank por $7.500 a pagar en tres meses, a una
TEC de 10%, ¿qué cantidad deberá pagar por concepto de intereses? Rpta. $555,75
3. ¿De qué interés compuesto podrá disponerse el 20 de diciembre, si el 30 de marzo se invirtió
$5.000 a una TET del 5%? Rpta. $772,45
4. Por un préstamo que se solicitó al BBVA a pagar en un año, Carito pagó $625 de interés, ¿qué
cantidad se pidió prestado si el banco aplica una TEA del 25%. Rpta. $2.500
5. ¿A cuánto asciende un préstamo solicitado por El Universo S.A.C. al Interbank a pagar en tres
meses a una TEC de 10%, si el banco durante dicho periodo me cobró un interés de $555,75?
Rpta. $7.500
6. ¿A cuánto asciende una inversión que se efectúo el 30 de marzo a una TET del 5%, si para el
20 de diciembre se contaba con $772,45 de interés? Rpta. $5.000

91. 91
7. Por un préstamo de $2.500 que se solicitó al BBVA a pagar en un año, Carito pagó $625 de
interés, ¿qué TEA aplicó el banco? Rpta. TEA de 25%
8. El Universo S.A.C. solicitó un préstamo al Interbank por $7.500 a pagar en tres meses. Si el
banco le cobró $555,75 de interés, ¿qué TEC cobró el banco? Rpta. TEC de 10%
9. El 30 de marzo se efectúo una inversión por $5.000. Al 20 de diciembre había ganado
intereses por $772,45, ¿qué TET obtuvo el inversionista? Rpta. TET de 5%
10. Carito solicita un préstamo al BBVA por $2.500 a una TEA de 25%. Si el banco nos cobra $625,
¿cuántos años duró la deuda? Rpta. 1 año
11. El Universo S.A.C. solicitó un préstamo al Interbank por $7.500 a una TEC de 10%. Si el banco
le cobró $555,75 de interés, ¿cuántos meses se mantuvo la operación? Rpta. 3 meses
12. El 30 de marzo se efectúo una inversión por $5.000 a una TET de 5%. Si pasado cierto tiempo
he ganado $772,45 de interés, ¿cuántos días se mantuvo la inversión? Rpta. 265 días
Interés con principal constante y tasa efectiva variable
13. El 30 de marzo se deposita en una cuenta $12.000 bajo un régimen de interés compuesto. La
TES vigente al momento del depósito fue de 15%, la misma que bajó a 14% el 09 de julio y
a 13% el 25 de octubre. La cuenta se cierra el 20 de diciembre, calcule el interés en la fecha
de cierre. Rpta. $2.584,64
14. El 30 de marzo se deposita en una cuenta $12.000, en un banco que paga una tasa de interés
efectiva variable. La cuenta se cierra el 20 de diciembre. Al término del plazo se conoce que
las tasas de interés fueron las siguientes:
Tasa A partir del
TEA
32,250%
30/03
TES
14,000%
09/07
TET 6,301% 25/10
Calcule el interés en la fecha de cierre. Rpta. $2.584,64
Monto o valor futuro compuesto con principal y tasa efectiva constante
15. Carito solicita un préstamo al BBVA por $2.500 a pagar en un año, a una TEA de 25%, ¿qué
monto deberá pagar al final del plazo? Rpta. $3.125
16. El Universo S.A.C. solicita un préstamo al Interbank por $7.500 a pagar en tres meses, a una
TEC de 10%, ¿qué monto deberá pagar al final del plazo? Rpta. $8.055,75
17. ¿De qué monto podrá disponerse el 20 de diciembre, si el 30 de marzo se invirtió $5.000 a
una TET del 5%? Rpta. $5.772,45

92. 92
Monto o valor futuro compuesto con principal constante y tasa nominal efectiva
18. El 30 de marzo se deposita en una cuenta $12.000 bajo un régimen de interés compuesto. La
TES vigente al momento del depósito fue de 15%, la misma que bajó a 14% el 09 de julio y
a 13% el 25 de octubre. La cuenta se cierra el 20 de diciembre, calcule el monto en la fecha
de cierre. Rpta. $14.584,64
19. El 30 de marzo se deposita en una cuenta $12.000, en un banco que paga una tasa de interés
efectiva variable. La cuenta se cierra el 20 de diciembre. Al término del plazo se conoce que
las tasas de interés fueron las siguientes:
Tasa A partir del
TEA 32,250% 30/03
TES 14,000% 09/07
TET 6,301% 25/10
Calcule el monto en la fecha de cierre. Rpta. $14.584,64
Valor presente o valor actual compuesto con principal y tasa efectiva constante
20. Carito solicita un préstamo al BBVA a pagar en un año. Si el banco cobra una TEA de 25% y
el monto a pagar al final del plazo asciende a $3.125, ¿qué principal solicitó Carito al BBVA?
Rpta. $2.500
21. El Universo S.A.C. solicita un préstamo al Interbank a pagar en tres meses. Si el banco cobra
una TEC de 10% y el monto a pagar al final del plazo asciende a $8.055,75, ¿qué principal fue
solicitado por El Universo S.A.C. al Interbank? Rpta. $7.500
22. ¿Qué principal tuvo que ser depositado el 30 de marzo, si fue invertido a una TET del 5%, para
que el 20 de diciembre tenga un monto de $5.772,45? Rpta. $5.000
Valor presente o valor actual compuesto con principal constante y tasa efectiva variable
23. El 30 de marzo se efectúa un depósito bajo un régimen de interés compuesto. La TES vigente
al momento del depósito fue de 15%, la misma que bajó a 14% el 09 de julio y a 13% el
25 de octubre. La cuenta se cierra el 20 de diciembre, la misma que ascendía a un monto de
$14.584,64. Calcule la cantidad que tuvo que depositarse el 30 de marzo. Rpta. $12.000
24. El 30 de marzo se abre una cuenta en un banco que paga una tasa de interés efectiva
variable. La cuenta se cierra el 20 de diciembre. Al término del plazo el monto de la cuenta
asciende a $14.584,64; así mismo, se conoce que las tasas de interés fueron las siguientes:
Tasa A partir del
TEA 32,250% 30/03
TES 14,000% 09/07
TET 6,301% 25/10
Calcule la cantidad que fue depositado en el banco. Rpta. $12.000

93. 93
Ecuaciones de valor equivalentes
25. Una persona tiene una deuda que debe ser saldada de la siguiente manera: $5.200 en este
momento y $5.200 dentro de dos meses. Si desea pagar su deuda completamente dentro de
30 días, ¿cuánto tendrá que pagar, si la TEA es de 20%? Rpta. $10.401,20
26. Textiles Pacífico S.A.C. tiene una deuda con el BSHC una deuda de $7.500 que vence el 15 de
marzo y otra deuda de $12.500 que vence el 15 de abril. La empresa renegoció con el banco
y consolidó sus deudas en una sola cuenta a interés simple con vencimiento al 25 de abril
del mismo año, a una TET constante de 5%. Se requiere saber el monto que cancelará Textiles
Pacífico S.A.C. el 25 de abril. Rpta. $20.236,52
27. Verónica Kamila solicitó en préstamo $2.500 que se registra en una cuenta a interés simple
que genera una TET de 8% para cancelarlo dentro de 90 días. La señorita Verónica se adelanta
al vencimiento del préstamo y amortiza $500 el día 30 y $1.000 el día 70, ¿cuánto deberá
pagar el día 90 para cancelar su deuda? Rpta. $1.156,43
Interés compuesto con tasa j capitalizable
28. Carlos Fernández deposita en una cuenta de ahorros del Interbank la suma de $2.500. Calcule
los intereses que obtendrá Carlos después de un año si el banco aplica una TNS de 12% con
capitalización mensual. Rpta. $670,60
29. Pedro Gonzáles deposita en una cuenta a plazo fijo del BWS la suma de $5.000. Calcule los
intereses que obtendrá Kamila después de un año si el banco aplica una TNT de 4% con
capitalización diaria. Rpta. $867,35
30. Carlos Fernández deposita en una cuenta de ahorros del Interbank la suma de $2.500. Calcule
el monto que obtendrá Carlos después de un año si el banco aplica una TNS de 12% con
capitalización mensual. Rpta. $3.170,60
31. Pedro Gonzáles deposita en una cuenta a plazo fijo del BWS la suma de $5.000. Calcule
el monto que obtendrá Pedro después de un año si el banco aplica una TNT de 4% con
capitalización diaria. Rpta. $5.867,35
32. Carlos Fernández depositó en una cuenta de ahorros del Interbank durante un año. Si el banco
aplicó una TNS de 12% con capitalización mensual y el monto obtenido al final del plazo
asciende a $3.170,60. Calcule el principal que depositó Carlos hace un año. Rpta. $2.500
33. Pedro Gonzáles depositó en una cuenta de ahorros del BWS durante un año. Si el banco aplicó
una TNT de 4% con capitalización diaria y el monto obtenido al final del plazo asciende a
$5.867,35. Calcule el principal que depositó Pedro hace un año. Rpta. $5.000

95. OPERACIONES DE DESCUENTO, TASAS, INFLACIÓN Y
DEVALUACIÓN Y LAS SEIS LLAVES MAESTRAS DE LAS
MATEMÁTICAS FINANCIERAS
Sesión Nº 4: Operaciones de descuento
Sesión Nº 5: Tasas
Sesión Nº 6: Inflación y devaluación
Sesión Nº 7: Las seis llaves maestras de las matemá-
ticas financieras
UNIDAD
III
UNIDAD III

96. COMPETENCIAS
CONCEPTUAL PROCEDIMENTAL ACTITUDINAL
Estudian las operacio-
nes de descuento, ta-
sas, inflación y deva-
luación y las seis llaves
maestras de las mate-
máticas financieras.
Construyen organizado-
res visuales para el de-
sarrollo de las operacio-
nes matemáticas.
Respetan los resultados
de las distintas opera-
ciones financieras.

97. Cálculo financiero
P R O E S A D
97
4
Sesión
operaciones de
descuento
1. INTRODUCCIÓN
En el sistema financiero una operación de descuento consiste en obtener el pago anticipado de
títulos valores: letras de cambio, pagarés u otros documentos, mediante la cesión o endoso del
derecho del poseedor a otra persona natural o jurídica. Esto, además de permitir al prestamista
disponer de inmediato del dinero correspondiente a los intereses, le da un mayor rendimiento que
la tasa señalada en la operación. De hecho, las tasas de interés para operaciones de descuento
son las más altas del sistema financiero peruano.
De esto, se puede señalar que la operación financiera de descuento es la inversa a la operación
de capitalización. Con esta operación se calcula el capital equivalente en un momento anterior
de un importe futuro.
Descontar un título-valor, es la acción de recibir o pagar hoy un dinero, a cambio de una suma
mayor comprometida para una fecha futura, bajo las condiciones convenidas en el título-valor. Un
título valor (letras, pagaré, etc.) como un bien mobiliario puede ser vendido, es decir descontado,
una o más veces antes de la fecha de su vencimiento y cada comprador descuenta el título-valor
por el tiempo que falta para su vencimiento.
Mientras que la ley de capitalización calcula unos intereses que se les añade al importe principal,
compensando el aplazamiento en el tiempo de su disposición. En las leyes de descuento es justo
al contrario: se calculan los intereses que hay que pagar por adelantar la disposición del capital.
Para estas operaciones, se usan ciertas expresiones léxicas que es necesario conocer:
a) Descuento: Es la diferencia entre el valor nominal y el valor que se recibe, en el momento
de descontar el título-valor. Se simboliza por la D.
b) Tasa de descuento: Es el tanto por ciento de descuento, o sea, el porcentaje del valor nominal
que deduce el prestamista, al descontar el título-valor. Es simbolizada por la d.
c) Plazo: Es el término que se utiliza para expresar el periodo de duración del préstamo. Se
simboliza por la n.
d) Valor descontado o valor presente de un título-valor: Es el valor nominal menos el descuento.
Es el valor en dinero que se recibe en el momento de descontar la obligación o, en otras
palabras, es el valor efectivo o líquido. El valor descontado es simbolizada por la P.

98. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
98
e) Valor nominal de un título-valor: El valor nominal del título-valor a descontar es el que
está inscrito en la obligación. Si el título-valor no gana intereses, el valor nominal indica la
cantidad que debe pagarse en la fecha de vencimiento señalada. Es simbolizada por la S.
Dentro de las leyes de descuento, se pueden distinguir tres modelos:
A continuación, vamos a empezar con el estudio del descuento comercial.
2. DESCUENTO COMERCIAL
Es la rebaja concedida sobre el precio de lista de un artículo que se oferta. El interés que se
aplica es un interés simple, el cual tiene el mismo tratamiento que el descuento bancario en su
modalidad simple que veremos en breve.
De esto, es usual que las empresas fabricantes y los mayoristas proporcionen a sus clientes listas
de precios propuestos por cada producto. El precio mostrado en estas listas es el llamado precio
de lista y es el precio sugerido para menudeo, esto es, el precio de lista puede o no ser el precio
final a pagar por el consumidor.
Las empresas fabricantes y los mayoristas venden a sus productos a los minoristas con un
descuento basado en el precio de lista, llamado descuento comercial. El descuento comercial
es un porcentaje del precio de lista, y recibe el nombre de tasa de descuento. El precio de lista
menos el descuento comercial se llama precio neto.
Los descuentos comerciales se aplican generalmente a las ventas hechas por el fabricante al
mayorista; por el mayorista al minorista y cuando el fabricante vende directamente al minorista.
Los descuentos pueden ser simples o unitarios y en cadena o sucesivos.
2.1. Descuento comercial unitario
En las operaciones comerciales, es costumbre ofrecer una rebaja sobre el precio de lista por
alguna razón; por ejemplo: promociones especiales de venta; por compras al por mayor; por
pronto pago y por otras causas que sería inoficioso enumerar.
Para calcular el descuento comercial unitario, podemos utilizar la fórmula siguiente:
D = S * d (1)
Clases de descuento5
Comercial Bancario Racional
Unitario Sucesivo Simple Compuesto Simple Compuesto
5
Cuadro tomado del libro “Funciones y herramientas de Excel para la gestión financiera”, de Carlos Aliaga Valdez y Carlos
Aliaga Calderón, reconocidos profesores de finanzas.

99. Cálculo financiero
P R O E S A D
99
Donde:
“ D ” son los intereses de descuento. La diferencia entre S y P
“ S ” es el capital final o valor nominal del título valor
“ d ” es la tasa de descuento que se aplica
Una vez que conocemos el importe del descuento, se puede calcular el valor descontado o
valor presente (que equivale al capital final (S) menos el importe del descuento (D)). Para esto
podemos utilizar cualquiera de las dos fórmulas siguientes:
P = S - D (2)
Sustituyendo “D” por su equivalencia, tenemos:
P = S - (S * d)
Sacando factor común “S”, tenemos:
P = S[1 - d] (3)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Calcular los intereses de descuento comercial que aplica Tiendas Carsa por un artefacto,
cuyo precio de lista es de $478, si se aplica un descuento comercial de 23%. Asimismo,
calcular el valor descontado.
Solución:
Los datos son:
D = ?
S = $478
d = 23%
Sustituyendo los valores numéricos en la ecuación (1) y (3), se obtiene:
D = 478 * 0,23 = $109,94
P = 478[1 - 0,23] = $368,06
El descuento asciende a $109,94. De esta manera el valor descontado del artefacto
asciende a $368,06 
2.2. Descuento comercial sucesivo o en cadena
Con frecuencia, ocurre que, sobre una misma factura, se hacen varios descuentos por diferentes
razones independientes entre sí. Estos descuentos sucesivos reciben el nombre de descuento en

100. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
100
cadena o en serie. Por ser los descuentos independientes, cada uno de ellos se efectúa sobre el
valor bruto de la factura, después de deducir el descuento anterior.
Para calcular el descuento sucesivo, podemos utilizar la fórmula siguiente:
D = S[1 - (1 - d1
)(1 - d2
),...,(1 - dn
)] (4)
El valor descontado o valor presente en un descuento comercial sucesivo o en cadena se puede
calcular utilizando la fórmula siguiente:
P = S[(1 - d1
)(1 - d2
),...,(1 - dn
)] (5)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Sobre una factura de $50.000 se conceden los siguientes descuentos.
a) Por compra al por mayor 8%
b) Por promoción especial de ventas 5%
c) Por despachos sin empaques 6%
Calcule los intereses de descuento comercial y el valor descontado.
Solución:
Los datos son:
D = ?
S = $50.000
d1
= 8%, d2
= 5%, d3
= 6%
Estos descuentos en cadena operan así:
El valor neto de la factura asciende a $41.078. Por tanto, los intereses de descuento
ascienden a $8.922.
El mismo resultado se puede calcular, sustituyendo los valores en la ecuación (4).
D = 50.000[1 - (1 - 0,08)(1 - 0,05)(1 - 0,06)] = $8.922
Para el cálculo del valor descontado se aplica la ecuación (5) y se obtiene:
Valor bruto de
factura
%
Descuento
Valor neto de
factura
$50.000 8% $46.000
$46.000 5% $43.700
$43.700 6% $41.078

101. Cálculo financiero
P R O E S A D
101
P = 50.000[1 - 0,08)(1 - 0,05)(1 - 0,06)] = $41.078
Por tanto, los intereses de descuento ascienden a $8.922 y el valor descontado a $41.078. 
3. DESCUENTO BANCARIO
El descuento bancario es el interés calculado sobre el valor nominal o valor futuro del título-valor
aplicando una tasa adelantada (d), importe que al deducirse de su respectivo valor nominal nos
permite encontrar el valor líquido que dispondrá en el presente el descontante del título-valor.
3.1. Descuento bancario simple
El descuento bancario simple es el producto del valor nominal del título-valor por la tasa
anticipada nominal d, y por el número de períodos que faltan para el vencimiento del descuento.
Descuento con tasa d nominal constante
Para el cálculo de este descuento, se aplica la siguiente fórmula:
D = S * d *n (6)
El valor descontado o valor presente en un descuento bancario simple se puede calcular utilizando
la fórmula siguiente:
P = S[1 - (d * n)] (7)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Calcular los intereses de descuento bancario simple que aplica el Banco Citibank por una
letra de cambio que asciende a $2.000, faltando un año para su vencimiento. El banco
cobra una TNA del 15%. Asimismo, calcular el valor descontado.
Solución:
Los datos son:
D = ?
S = $2.000
d = 15%
n = 1 año
Sustituyendo los valores numéricos en la ecuación (6), se obtiene:
D = 2.000 * 0,15 * 1 = $300
Para calcular el valor descontado, se aplica la ecuación (7) y se tiene:
P = 2.000[1 - (0,15 * 1)] = $1.700

102. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
102
El descuento asciende a $300. El valor descontado o valor presente, asciende a $1.700, el cual
quiere decir que una letra de cambio cuyo valor nominal o valor de vencimiento es de $2.000,
equivale a $1.700, faltando un año para su vencimiento y aplicando una tasa del 15% anual. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el
BCP, cuando faltaba cuatro meses para su vencimiento. Se requiere conocer el importe
del descuento bancario simple que efectúo el banco que aplicó una TNS de descuento
anticipada de 18%. Se pide también calcular el valor descontado.
Solución:
Los datos son:
D = ?
S = 5.000
d = 18%
n = 4 meses
Sustituyendo los valores numéricos en la ecuación (6), se obtiene:
D
= =
5 000 0 18
120
180
600
. * , * $
Para calcular el valor descontado, se aplica la ecuación (7) y se tiene:
P = −











 =
5 000 1 0 18
120
180
4 400
. , * $ .
El descuento asciende a $600. El valor descontado o valor presente, asciende a $4.400, el
cual quiere decir que una letra cuyo valor nominal o valor de vencimiento es de $5.000,
equivale a $4.400, faltando cuatro meses para su vencimiento y aplicando una TNS de
18%. 
Ejemplo 3
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el BCP,
cuando faltaba 287 días para su vencimiento. Se requiere conocer el importe del descuento
bancario simple que efectúo el banco que aplicó una TNM de descuento anticipada de 2%.
Calcule también el valor descontado.
Solución:

103. Cálculo financiero
P R O E S A D
103
Sustituyendo los valores numéricos en la ecuación (6), se obtiene:
D
= =
5 000 0 02
287
30
956 67
. * , * $ ,
Para calcular el valor descontado, aplicamos la ecuación (7) y se tiene:
P = −











 =
5 000 1 0 02
287
30
4 043 33
. , * $ . ,
El descuento asciende a $956,67. El valor descontado o valor presente, asciende a
$4.043,33, el cual quiere decir que una letra cuyo valor nominal o valor de vencimiento es
de $5.000, equivale a $4.043,33, faltando 287 días para su vencimiento y aplicando una
TNM de 2%. 
Descuento con tasa d nominal variable
Ahora, muchas veces sucede que las tasas nominales sufren variaciones durante el plazo del
descuento, para esta situación, utilizamos la fórmula siguiente.
D S d
h
F
k
k
k
k
z
=






=
∑ *
1
(8)
Donde:
“ z ” es el número de subhorizontes, donde la j no sufre variaciones
“ dk ” es la tasa nominal anunciada vigente en k-ésimo horizonte
“ nk ” es el número de períodos de la tasa jk en k-ésimo horizonte
“ F ” es el plazo de la tasa de interés nominal
El valor descontado o valor presente en un descuento bancario simple cuando las tasas o los
periodos de tasa son variables es la siguiente:
P S d
h
F
k
k
k
k
z
= −














=
∑
1
1
* (9)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado, cuando el principal es
constante y la tasa nominal variable
Calcule el descuento bancario simple que se efectuará a un pagaré con valor nominal de
$10.000. El pagaré se descontará el 4 de mayo y vencerá el 16 de septiembre del mismo
año. La TNA será del 12% hasta el 30 de junio y a partir de esa fecha se incrementará al
15%.
Solución:

104. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
104
Los datos son:
D = ?
S = 10.000
d1
= 12%
d2
= 15%
h1
= 57
h2
= 78
Sustituyendo los valores numéricos en la ecuación (8), se obtiene:
D = +





 =
10 000 0 12
57
360
0 15
78
360
515
. * , * , * $
Para el cálculo del valor descontado, aplicamos la ecuación (9) y se tiene:
P = − +











 =
10 000 1 0 12
57
360
0 15
78
360
9 485
. , * , * $ .
El descuento asciende a $515 y el valor descontado o valor presente a $9.485. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado cuando el principal es
constante y la tasa nominal variable
Calcule el descuento bancario simple que se efectuará a un pagaré con valor nominal de
$5.000. El pagaré se descontará el 13 de febrero y vencerá el 27 de noviembre del mismo
año. Al término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TNA 28,0% 13/02
TNS 12,5% 09/07
TNT 5,5% 20/09
Calcule el interés descuento en la fecha de cierre.
Solución:
Los datos son:
D = ?
S = 5.000
d1
= 28%
d2
= 12,5%
d3
= 5,5%
h1
= 146
h2
= 73
h3
= 68

105. Cálculo financiero
P R O E S A D
105
Sustituyendo los valores numéricos en la ecuación (8), se obtiene:
D = + +





 =
5 000 0 28
146
360
0 125
73
180
0 055
68
90
1 029 03
. * , * , * , * $ . ,
Para el cálculo del valor descontado, aplicamos la ecuación (9) y se tiene:
P = − + +











 =
5 000 1 0 28
146
360
0 125
73
180
0 055
68
90
3
. , * , * , * $ .
. ,
970 97
El descuento asciende a $1.029,03 y el valor descontado o valor presente a $3.970,97. 
3.2. Descuento bancario compuesto
El descuento bancario compuesto es una sucesión de operaciones de descuento bancario simple,
en las que después de la primera, su valor líquido se constituye en el valor nominal de la
siguiente, y así sucesivamente hasta llegar a la fecha del descuento.
Descuento con tasa i efectiva constante
Para el cálculo de este descuento, se aplica la siguiente fórmula:
D = S[1 - (1 - d)n
] (10)
El valor descontado o valor presente en un descuento bancario compuesto se puede calcular
utilizando la fórmula siguiente:
P = S[(1 - d)n
] (11)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Calcular los intereses de descuento bancario compuesto que aplica el Banco Citibank por
una letra de cambio que asciende a $2.000, faltando un año para su vencimiento. El banco
cobra una TEA del 15%.
Solución:
Los datos son:
D = ?
S = $2.000
d = 15%
n = 1 año
Sustituyendo los valores numéricos en la ecuación (10), se obtiene:

106. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
106
D = 2.000[1 - (1 - 0,15)] = $300
Aplicando la ecuación (11) para el cálculo del valor descontado se tiene:
P = 2.000(1 - 0,15) = $1.700
El descuento asciende a $300 y el valor descontado o valor presente, asciende a $1.700. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el BCP,
cuando faltaba cuatro meses para su vencimiento. Se requiere conocer el importe del
descuento bancario compuesto que efectúo el banco que aplicó una TES de descuento
anticipada de 18%.
Solución:
Los datos son:
D = ?
S = 5.000
d = 18%
n = 4 meses
Sustituyendo los valores numéricos en la ecuación (10), se obtiene:
D = − −
( )





 =
5 000 1 1 0 18 619 61
120
180
. , $ ,
Aplicando la ecuación (11) para el cálculo del valor descontado se tiene:
P = −
( )





 =
5 000 1 0 18 4 380 39
120
180
. , $ . ,
El descuento asciende a $619,61 y el valor descontado o valor presente a $4.380,39. 
Ejemplo 3
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el
BCP, cuando faltaba 287 días para su vencimiento. Se requiere conocer el importe del
descuento bancario compuesto que efectúo el banco que aplicó una TEM de descuento
anticipada de 2%.

107. Cálculo financiero
P R O E S A D
107
Solución:
Sustituyendo los valores numéricos en la ecuación (10), se obtiene:
D = − −
( )





 =
5 000 1 1 0 02 878 71
287
30
. , $ ,
Aplicando la ecuación (11) para el cálculo del valor descontado se tiene:
P = −
( )





 =
5 000 1 0 18 4 380 39
120
180
. , $ . ,
El descuento asciende a $878,71 y el valor descontado o valor presente a $4.121,29. 
Descuento con tasa i efectiva variable
Ahora, muchas veces sucede que las tasas efectivas sufren variaciones durante el plazo del
descuento, para esta situación, utilizamos la fórmula siguiente.
D S ik
h F
k
z
k k
= − −
( )






=
∏
1 1
1
(12)
El valor descontado o valor presente en un descuento bancario compuesto cuando las tasas o los
periodos de tasa son variables es la siguiente:
D S ik
h F
k
z
k k
= −
( )






=
∏ 1
1
(13)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado cuando el principal es
constante y la tasa efectiva variable
Calcule el descuento bancario compuesto que se efectuará a un pagaré con valor nominal
de $10.000. El pagaré se descontará el 4 de mayo y vencerá el 16 de septiembre del mismo
año. La TEA será del 12% hasta el 30 de junio y a partir de esa fecha se incrementará al
15%.
Solución:
Los datos son:
D = ?
S = 10.000
d1
= 12%
d2
= 15%
h1
= 57
h2
= 78

108. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
108
Sustituyendo los valores numéricos en la ecuación (12), se obtiene:
D = − −
( ) −
( )





 =
10 000 1 1 0 12 1 0 15 539 43
57
360
78
360
. , , $ ,
Al aplicar la ecuación (13) para encontrar el valor descontado, se tiene:
D = −
( ) −
( )





 =
10 000 1 0 12 1 0 15 9 460 57
57
360
78
360
. , , $ . ,
El descuento asciende a $539,43 y el valor descontado o valor presente a $9.460,57. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado cuando el principal es
constante y la tasa efectiva variable
Calcule el descuento bancario compuesto que se efectuará a un pagaré con valor nominal
de $5.000. El pagaré se descontará el 13 de febrero y vencerá el 27 de noviembre del
mismo año. Al término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TEA 28,0% 13/02
TES 12,5% 09/07
TET 5,5% 20/09
Calcule el interés descuento en la fecha de cierre.
Solución:
Los datos son:
D = ?
S = 5.000
d1
= 28%
d2
= 12,5%
d3
= 5,5%
h1
= 146
h2
= 73
h3
= 68
Sustituyendo los valores numéricos en la ecuación (12), se obtiene:
D = − −
( ) −
( ) −
( )





 =
5 000 1 1 0 28 1 0125 1 0 055 1
146
360
73
180
68
90
. , , $ .
. ,
027 82

109. Cálculo financiero
P R O E S A D
109
Al aplicar la ecuación (13) para encontrar el valor descontado, se tiene:
P = −
( ) −
( ) −
( )





 =
5 000 1 0 28 1 0 125 1 0 055 3
146
360
73
180
68
90
. , , , $ .9
972 18
,
El descuento asciende a $1.027,82 y el valor descontado o valor presente a $3.972,18. 
4. DESCUENTO RACIONAL
El descuento racional efectuado al valor nominal de un título-valor que vence en el futuro,
es su respectivo interés deducido por anticipado, calculado con la tasa de interés nominal j o
con la tasa de interés efectiva i sobre el importe que verdaderamente recibe el descontante;
este importe constituye el valor presente del título-valor. De este modo, el descuento racional
calculado sobre el valor nominal del título-valor y el interés vencido calculado sobre su respectivo
valor presente durante un mismo plazo, con la misma tasa, producen iguales resultados; incluso,
se ha comprobado la identidad Descuento = Interés.
Este descuento se denomina racional, matemático o verdadero porque existe perfecta
reversibilidad entre sus variables, lo que significa que a través de la tasa de descuento (tasa j
o tasa i) el valor del título-valor puede convertirse en un valor presente y viceversa; lo que no
sucede con el descuento bancario, como veremos más adelante. El descuento racional puede ser
simple o compuesto.
4.1. Descuento racional simple
Este tipo de descuento, obtiene el descuento racional simple efectuado al valor nominal de un
título-valor que vence en una fecha futura aplicando una tasa nominal j de cualquier plazo, por
el período de tiempo que media entre la fecha de vencimiento del título-valor y el momento en
que se descuento dicho título.
Descuento con tasa d nominal constante
Para el cálculo de este descuento, se aplica la siguiente fórmula:
D S
dn
= −
+






1
1
1
(14)
Este tipo de descuento produce el mismo resultado que el interés simple calculado sobre el valor
presente del título-valor, siendo el valor presente la diferencia del valor nominal y el importe
del descuento.
El valor descontado o valor presente en un descuento racional simple se puede calcular utilizando
la fórmula siguiente:
P S
dn
=
+






1
1
(15)
Si la formula anterior, le parece algo conocida, está en lo cierto. La formula es idéntica, cuando

110. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
110
calculamos el valor presente utilizando interés simple. Por tanto, este tipo de descuento produce
el mismo resultado que el interés simple calculado sobre el valor presente del título-valor.
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Calcular los intereses de descuento racional simple que aplica el Banco Citibank por una
letra de cambio que asciende a $2.000, faltando un año para su vencimiento. El banco
cobra una TNA del 15%.
Solución:
Los datos son:
D = ?
S = $2.000
d = 15%
n = 1 año
Sustituyendo los valores numéricos en la ecuación (14), se obtiene:
D = −
+





 =
2 000 1
1
1 0 15 1
260 87
.
, *
$ ,
Sustituyendo los valores en la ecuación (15) para calcular el valor descontado se tiene:
D =
+





 =
2 000
1
1 0 15 1
1 739 13
.
, *
$ . ,
El descuento asciende a $260,87 y el valor descontado o valor presente a $1.739,13. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor nominal de $5.000 fue descontada por el BCP, cuando
faltaba cuatro meses para su vencimiento. Se requiere conocer el importe del descuento
racional simple que efectúo el banco que aplicó una TNS de descuento anticipada de 18%.
Solución:
Los datos son:
D = ?
S = 5.000
d = 18%
n = 4 meses

111. Cálculo financiero
P R O E S A D
111
Sustituyendo los valores numéricos en la ecuación (14), se obtiene:
D = −
+












=
5 000 1
1
1 0 18
120
180
535 71
.
, *
$ ,
Sustituyendo los valores en la ecuación (15) para calcular el valor descontado se tiene:
P =
+












=
5 000
1
1 0 18
120
180
4 464 29
.
, *
$ . ,
El descuento asciende a $535,71 y el valor descontado o valor presente a $4.464,29. 
Ejemplo 3
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor nominal de $5.000 fue descontada por el BCP,
cuando faltaba 287 días para su vencimiento. Se requiere conocer el importe del descuento
racional simple que efectúo el banco que aplicó una TNM de descuento anticipada de 2%.
Solución:
Sustituyendo los valores numéricos en la ecuación (14), se obtiene:
D = −
+












=
5 000 1
1
1 0 02
287
30
803 02
.
, *
$ ,
Sustituyendo los valores en la ecuación (15) para calcular el valor descontado se tiene:
P =
+












=
5 000
1
1 0 02
287
30
4 196 98
.
, *
$ . ,
El descuento asciende a $803,02 y el valor descontado o valor presente, asciende a
$4.196,98. 
Descuento con tasa d nominal variable
La fórmula para calcular el descuento cuando las tasas nominales sufren variaciones, es la

112. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
112
siguiente.
D S
d
h
F
k
k
k
k
z
= −
+




















=
∑
1
1
1
1
*
(16)
El valor descontado o valor presente en un descuento racional simple cuando las tasas o los
periodos de tasa son variables es la siguiente:
P S
d
h
F
K
k
k
k
z
=
+




















=
∑
1
1
1
*
(17)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado cuando el principal es
constante y la tasa nominal variable
Calcule el descuento racional simple que se efectuará a un pagaré con valor nominal de
$10.000. El pagaré se descontará el 4 de mayo y vencerá el 16 de septiembre del mismo
año. La TNA será del 12% hasta el 30 de junio y a partir de esa fecha se incrementará al
15%.
Solución:
Los datos son:
D = ?
S = 10.000
d1
= 12%
d2
= 15%
h1
= 57
h2
= 78
Sustituyendo los valores numéricos en la ecuación (16), se obtiene:
D = −
+ +












=
10 000 1
1
1 0 12
57
360
0 15
78
360
489 78
.
, * , *
$ ,
Al aplicar la ecuación (17) para encontrar el valor descontado, se tiene:
P =
+ +












=
10 000
1
1 0 12
57
360
0 15
78
360
9 510 22
.
, * , *
$ . ,

113. Cálculo financiero
P R O E S A D
113
El descuento asciende a $489,78 y el valor descontado o valor presente a $9.510,22. 
Ejemplo 2
Cálculo del interés del descuento y del valor descontado cuando el principal es
constante y la tasa nominal variable
Calcule el descuento racional simple que se efectuará a un pagaré con valor nominal de
$5.000. El pagaré se descontará el 13 de febrero y vencerá el 27 de noviembre del mismo
año. Al término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TNA 28,0% 13/02
TNS 12,5% 09/07
TNT 5,5% 20/09
Calcule el interés descuento en la fecha de cierre.
Solución:
Los datos son:
D = ?
S = 5.000
d1
= 28%
d2
= 12,5%
d3
= 5,5%
h1
= 146
h2
= 73
h3
= 68
Sustituyendo los valores numéricos en la ecuación (16), se obtiene:
D = −
+ + +












5 000 1
1
1 0 28
146
360
0 125
73
180
0 055
68
90
.
, * , * , *
=
= $ ,
853 39
Al aplicar la ecuación (17) para encontrar el valor descontado, se tiene:
P =
+ + +












=
5 000
1
1 0 28
146
360
0 125
73
180
0 055
68
90
.
, * , * , *
$4
4 146 61
. ,
El descuento asciende a $853,39 y del valor descontado o valor presente a $4.146,61. 

114. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
114
4.2. Descuento racional compuesto
Este tipo de descuento obtiene el descuento racional compuesto efectuado al valor nominal de
un título-valor que vence en una fecha futura aplicando una tasa efectiva de cualquier plazo, por
el período de tiempo que media entre la fecha de vencimiento del título-valor y el momento en
que se descuento dicho título.
El descuento racional compuesto es el único tipo de descuento en el que la tasa de descuento que
se anuncia es la que efectivamente se cobra, lo que no sucede con los otros descuentos que se
han tratado anteriormente. En el sistema financiero peruano este descuento es el único permitido
por las entidades reguladoras del sistema, por lo que su aplicación es de uso obligatorio.
El descuento racional compuesto produce el mismo resultado que el interés compuesto calculado
sobre el valor presente del título-valor, siendo el valor presente la diferencia del valor nominal
y el importe del descuento
Descuento con tasa i efectiva constante
Para el cálculo de este descuento, se aplica la siguiente fórmula:
D = S[1 - (1 + d)-n
] (18)
El valor descontado o valor presente en un descuento racional compuesto se puede calcular
utilizando la fórmula siguiente:
P = S[(1+ d)-n
] (19)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Calcular los intereses de descuento racional compuesto que aplica el Banco Citibank por
una letra de cambio que asciende a $2.000, faltando un año para su vencimiento. El banco
cobra una TEA del 15%.
Solución:
Los datos son:
D = ?
S = $2.000
d = 15%
n = 1 año
Sustituyendo los valores numéricos en la ecuación (18), se obtiene:
D = 2.000[1 - (1 + 0,15)-1
] = $260,87

115. Cálculo financiero
P R O E S A D
115
Al aplicar la ecuación (19) para encontrar el valor descontado, se tiene:
P = 2.000[(1 + 0,15)-1] = $1.739,13
El descuento asciende a $260,87y del valor descontado o valor presente, asciende a
$1.739,13. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el BCP,
cuando faltaba cuatro meses para su vencimiento. Se requiere conocer el importe del
descuento racional compuesto que efectúo el banco que aplicó una TES de descuento
anticipada de 18%.
Solución:
Los datos son:
D = ?
S = 5.000
d = 18%
n = 4 meses
Sustituyendo los valores numéricos en la ecuación (18), se obtiene:
D = − +
( )





 =
−
5 000 1 1 0 18 522 37
120
180
. , $ ,
Al aplicar la ecuación (19) para encontrar el valor descontado, se tiene:
P = +
( )





 =
−
5 000 1 0 18 4 477 63
120
180
. , $ . ,
El descuento asciende a $522,37 y del valor descontado o valor presente a $4.477,63. 
Ejemplo 3
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el
BCP, cuando faltaba 287 días para su vencimiento. Se requiere conocer el importe del
descuento racional compuesto que efectúo el banco que aplicó una TEM de descuento
anticipada de 2%.

116. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
116
Solución:
Sustituyendo los valores numéricos en la ecuación (18), se obtiene:
D = − +
( )





 =
−
5 000 1 1 0 02 862 91
287
30
. , $ ,
Al aplicar la ecuación (19) para encontrar el valor descontado, se tiene:
P = +
( )





 =
5 000 1 0 02 4 137 09
287
30
. , $ . ,
El descuento asciende a $862,91 y del valor descontado o valor presente a $4.137,09. 
Descuento con tasa i efectiva variable
La fórmula para calcular el descuento cuando las tasas efectivas sufren variaciones, es la siguiente:
D S
dk
h F
k
z
k k
= −
+
( )












=
∏
1
1
1
1
(20)
El valor descontado o valor presente en un descuento bancario compuesto cuando las tasas o los
periodos de tasa son variables es la siguiente:
P S
dk
h F
k
z
k k
=
+
( )












=
∏
1
1
1
(21)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado cuando el principal es
constante y la tasa efectiva variable
Calcule el descuento racional compuesto que se efectuará a un pagaré con valor nominal
de $10.000. El pagaré se descontará el 4 de mayo y vencerá el 16 de setiembre del mismo
año. La TEA será del 12% hasta el 30 de junio y a partir de esa fecha se incrementará al
15%.
Solución:

117. Cálculo financiero
P R O E S A D
117
Los datos son:
D = ?
S = 10.000
d1
= 12%
d2
= 15%
h1
= 57
h2
= 78
Sustituyendo los valores numéricos en la ecuación (20), se obtiene:
D = −
+
( ) +
( )










=
10 000 1
1
1 0 12 1 0 15
470 86
57
360
78
360
.
, ,
$ ,
Sustituyendo los valores en la ecuación (21) para calcular el valor descontado se tiene:
P =
+
( ) +
( )










=
10 000
1
1 0 12 1 0 15
9 529 14
57
360
78
360
.
, ,
$ . ,
El descuento asciende a $470,86 y el valor descontado o valor presente a $9.529,14. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado cuando el principal es
constante y la tasa efectiva variable
Calcule el descuento racional compuesto que se efectuará a un pagaré con valor nominal de
$5.000. El pagaré se descontará el 13 de febrero y vencerá el 27 de noviembre del mismo
año. Al término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TEA 28,0% 13/02
TES 12,5% 09/07
TET 5,5% 20/09
Calcule el interés descuento en la fecha de cierre.
Solución:
Los datos son:
D = ?
S = 5.000
d1
= 28%

118. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
118
d2
= 12,5%
d3
= 5,5%
h1
= 146
h2
= 73
h3
= 68
Sustituyendo los valores numéricos en la ecuación (20), se obtiene:
D = −
+
( ) +
( ) +
( )







5 000 1
1
1 0 28 1 0 125 1 0 055
146
360
73
180
68
90
.
, , ,




= $ ,
662 54
Sustituyendo los valores en la ecuación (21) para calcular el valor descontado se tiene:
P =
+
( ) +
( ) +
( )









5 000
1
1 0 28 1 0 125 1 0 055
146
360
73
180
68
90
.
, , , 

= $ . ,
4 337 46
El descuento asciende a $662,54 y el valor descontado o valor presente a $4.337,46. 
Descuento con tasa j capitalizable
El descuento racional compuesto también puede ser generado por una tasa nominal j capitalizable
m veces (m es el número de periodos que capitaliza la tasa nominal en su respectivo plazo).
La formula que nos permite calcular los intereses de descuento es la siguiente:
D S
j
m
n
= − +














−
1 1 (22)
El valor descontado o valor presente en un descuento racional compuesto con j capitalizable se
puede calcular utilizando la fórmula siguiente:
P S
j
m
n
= +














−
1 (23)
Ejemplo 1
Cálculo del interés de descuento y del valor descontado
Calcular los intereses de descuento que aplica el Banco Citibank por una letra de cambio
que asciende a $2.000, faltando un año para su vencimiento. El banco cobra una TNA del
15% capitalizable mensualmente.
Solución:

119. Cálculo financiero
P R O E S A D
119
Los datos son:
D = ?
S = $2.000
d = 15%
n = 1 año
Sustituyendo los valores numéricos en la ecuación (22), se obtiene:
D = − +














=
−
2 000 1 1
0 15
12
276 98
360
30
.
,
$ ,
Sustituyendo los valores en la ecuación (23) para calcular el valor descontado se tiene:
P = +














=
−
2 000 1
0 15
12
1 723 02
360
30
.
,
$ . ,
El descuento asciende a $276,98 y el valor descontado o valor presente, asciende a
$1.723,02. 
Ejemplo 2
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el
BCP, cuando faltaba cuatro meses para su vencimiento. Se requiere conocer el importe
del descuento racional compuesto que efectúo el banco que aplicó una TES de 18%
capitalizable mensualmente.
Solución:
Los datos son:
D = ?
S = 5.000
d = 18%
n = 4 meses
Sustituyendo los valores numéricos en la ecuación (22), se obtiene:
D = − +














=
−
5 000 1 1
0 18
6
557 56
120
30
.
,
$ ,

120. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
120
Sustituyendo los valores en la ecuación (23) para calcular el valor descontado se tiene:
P = +














=
−
5 000 1
0 18
6
4 442 44
120
30
.
,
$ . ,
El descuento asciende a $557,56 y el valor descontado o valor presente a $4.442,44. 
Ejemplo 3
Cálculo del interés de descuento y del valor descontado
Una letra de cambio que tiene un valor de nominal de $5.000 fue descontada por el
BCP, cuando faltaba 287 días para su vencimiento. Se requiere conocer el importe del
descuento racional compuesto que efectúo el banco que aplicó una TEM de 2% capitalizable
mensualmente.
Solución:
Sustituyendo los valores numéricos en la ecuación (22), se obtiene:
D = − +
( )





 =
−
5 000 1 1 0 02 862 91
287
30
. , $ ,
Sustituyendo los valores en la ecuación (23) para calcular el valor descontado se tiene:
P = +
( )





 =
−
5 000 1 0 02 4 137 09
287
30
. , $ . ,
El descuento asciende a $862,91 y el valor descontado o valor presente a $4.137,09. 
5. OPERACIONES DE DESCUENTO EN LA PRÁCTICA
Resumiendo lo que hemos visto en las secciones anteriores, en el sistema financiero peruano solo
está permitido el uso del descuento racional compuesto, puesto que este tipo de descuento es
el único en el que la tasa de descuento que se anuncia es la que efectivamente se cobra, lo que
no sucede con los otros descuentos. Por tanto, en el sistema financiero peruano este descuento
es el único permitido por las entidades reguladoras del sistema, por lo que su aplicación es de
uso obligatorio.
Asimismo, hemos visto en los ejemplos anteriores que la institución financiera que descuenta el
título-valor, solo nos cobra la tasa de interés, y en la práctica esto no es así. Estas instituciones,
además de la tasa de interés nos cobran ciertas comisiones, gastos, seguros, impuestos, etc.
Las comisiones son cantidades que se pagan o cobran por la prestación de un servicio. La comisión
se expresa en tanto por ciento y en su valor no interviene el tiempo.

121. Cálculo financiero
P R O E S A D
121
Por tanto, los bancos en sus prácticas, además de la tasa de descuento, cobran otros tipos de
conceptos, los cuales al agregarse al descuento, disminuyen el valor efectivo del título-valor y
como consecuencia resulta más alta la tasa de interés de la operación. En otras palabras el costo
efectivo de la operación de descuento es mayor a la tasa que anuncia el banco para este tipo de
producto. Recuerde, la tasa efectiva está determinado por lo que efectivamente recibimos y lo
que efectivamente pagamos.
Ejemplo 1
Cálculo del interés (I)
Calcular el valor descontado o valor presente que se recibe al descontar un pagaré de
$5.000, 120 días antes de su vencimiento, si el banco cobra además $5 por gastos bancarios
y el 0,2% por concepto de comisiones, sobre el pagaré. El BWS aplica una TEA de 9%. El
banco abona el neto a la cuenta corriente de la empresa.
Solución:
Los datos son:
P = ?
S = $5.000
d = 9%
n = 120 días
En primer lugar, calculamos el valor descontado del pagaré. Sustituyendo los valores
numéricos en la ecuación (17), se obtiene:
P = +
( )





 =
−
5 000 1 0 09 4 858 41
120
360
. , $ . ,
A continuación, a este importe le restamos los gastos bancarios ($5) y las comisiones
($10). Por tanto, monto que el BWS abonará a la cuenta corriente de la empresa es como
sigue:
P = 4.858,41 - (5 + 10)
P = $4.843,41
El banco abonará a la cuenta corriente de la empresa la suma de $4.843,41.
Ahora, si queremos calcular el costo efectivo de la operación de descuento, veamos dos
escenarios:
a) Cuando el banco sólo me cobra la tasa de interés
La tasa efectiva a 120 días de esta operación es:
i =
−
= =
5 000 4 858 41
4 858 41
141 59
4 858 41
2 914
. . ,
. ,
,
. ,
. %

122. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
122
Para calcular la TEA, capitalizamos la tasa efectiva a 120 días, el cual es como sigue:
TEA = [(1 + 0,02914)3
- 1] = 9%
Podemos observar que cuando el banco solo me cobra la tasa que anuncia, entonces
esa tasa es la TEA.
b) Cuando el banco además de la tasa de interés me cobra gastos bancarios y comisiones
La tasa efectiva a 120 días de esta operación es:
i =
−
= =
5 000 4 843 41
4 843 41
156 59
4 843 41
3 233
. . ,
. ,
,
. ,
. %
Para calcular la tasa efectiva anual, capitalizamos la tasa efectiva a 120 días, el cual es
como sigue:
TEA = [(1 + 0,03233)3
- 1] = 10,01%
Lo contrario, podemos observar que cuando el banco, aparte de cobrarme la tasa de interés,
me cobra otros costos, entonces la tasa efectiva es mayor a la tasa que anuncia. 

123. 123
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Descuento comercial unitario
1. Calcular los intereses de descuento comercial y el valor descontado o precio neto que
aplica Saga Falabella por una cámara digital, cuyo precio de lista es de $350, si se aplica un
descuento comercial de 25%. Rpta. $87,50 y $262,50
Descuento comercial sucesivo o en cadena
2. Sobre una factura de $7.500 se conceden los siguientes descuentos.
a) Por compra al por mayor 6%
b) Por promoción especial de ventas 4%
c) Por despachos sin empaques 2%
Calcule los intereses de descuento comercial el valor descontado de la factura. Rpta. $867,36
y $6.632,64
Descuento bancario simple con tasa d nominal constante

124. 124
3. Calcular los intereses de descuento bancario simple que aplica el Banco Interfip por una letra
de cambio que asciende a $4.250, faltando un año para su vencimiento. Calcular también el
valor descontado o valor presente de la letra de cambio. El banco cobra una TNS del 12%.
Rpta. $1.020 y $3.230
4. Una letra de cambio que tiene un valor de nominal de $3.750 fue descontada por el BCP,
cuando faltaba cinco meses para su vencimiento. Calcular también el valor descontado o
valor presente de la letra de cambio. Se requiere conocer el importe del descuento bancario
simple que efectúo el banco que aplicó una TNT de descuento anticipada de 8,5%. Rpta.
$531,25 y $3.218,75
5. Una letra de cambio que tiene un valor de nominal de $8.820 fue descontada por el BCP,
cuando faltaba 136 días para su vencimiento. Calcular también el valor descontado o valor
presente de la letra de cambio. Se requiere conocer el importe del descuento bancario simple
que efectúo el banco que aplicó una TNQ de descuento anticipada de 1,25%. Rpta. $999,60
y $7.820,40
Descuento bancario simple con tasa d nominal variable
6. Calcule el descuento bancario simple que se efectuará a un pagaré con valor nominal de
$12.500. El pagaré se descontará el 13 de febrero y vencerá el 9 de julio del mismo año. La TNA
será del 14% hasta el 26 de mayo y a partir de esa fecha se incrementará al 16%. Asimismo,
calcular el valor descontado o valor presente del pagaré. Rpta. $740,28 y $11.759,72
7. Calcule el descuento bancario simple que se efectuará a un pagaré con valor nominal de
$25.000. El pagaré se descontará el 8 de enero y vencerá el 20 de octubre del mismo año. Al
término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TNS
8,0%
08/01
TNT
4,5%
26/05
TNQ
0,8%
05/09
Calcule el interés descuento en la fecha de cierre, así como el valor descontado o valor
presente del pagaré. Rpta. $3.408,33 y $21.591,67
Descuento bancario compuesto con tasa i efectiva constante
8. Calcular los intereses de descuento bancario compuesto que aplica el Banco Interfip por una
letra de cambio que asciende a $4.250, faltando un año para su vencimiento. A su vez calcule
el valor descontado o valor presente de la letra de cambio. El banco cobra una TES del 12%.
Rpta. $958,80 y $3.291,20
9. Una letra de cambio que tiene un valor de nominal de $3.750 fue descontada por el BCP,
cuando faltaba cinco meses para su vencimiento. Se requiere conocer el importe del descuento
bancario compuesto que efectúo el banco que aplicó una TET de descuento anticipada de
8,5%. A su vez calcule el valor descontado o valor presente de la letra de cambio. Rpta.
$516,05 y Rpta. $3.233,95

125. 125
10. Una letra de cambio que tiene un valor de nominal de $8.820 fue descontada por el BCP,
cuando faltaba 136 días para su vencimiento. Se requiere conocer el importe del descuento
bancario compuesto que efectúo el banco que aplicó una TEQ de descuento anticipada de
1,25%. A su vez calcule el valor descontado o valor presente de la letra de cambio. Rpta.
$950,66 y Rpta. $7.869,34
Descuento bancario compuesto con tasa i efectiva variable
11. Calcule el descuento bancario compuesto que se efectuará a un pagaré con valor nominal
de $12.500. El pagaré se descontará el 13 de febrero y vencerá el 9 de julio del mismo
año. La TEA será del 14% hasta el 26 de mayo y a partir de esa fecha se incrementará al
16%. Asimismo, calcular el valor descontado o valor presente del pagaré. Rpta. $775,44 y
$11.724,56
12. Calcule el descuento bancario compuesto que se efectuará a un pagaré con valor nominal de
$25.000. El pagaré se descontará el 8 de enero y vencerá el 20 de octubre del mismo año. Al
término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TES
8,0%
08/01
TET
4,5%
26/05
TEQ
0,8%
05/09
Calcule el interés descuento en la fecha de cierre, así como el valor descontado o valor
presente del pagaré. Rpta. $3.270,51 y Rpta. $21.729,49
Descuento racional simple con tasa d nominal constante
13. Calcular los intereses de descuento racional simple que aplica el Banco Interfip por una letra
de cambio que asciende a $4.250, faltando un año para su vencimiento. Asimismo, calcular
el valor descontado o valor presente de la letra de cambio pagaré. El banco cobra una TES
del 12%. Rpta. $822,58 y $3.427,42
14. Una letra de cambio que tiene un valor de nominal de $3.750 fue descontada por el BCP,
cuando faltaba cinco meses para su vencimiento. Se requiere conocer el importe del descuento
racional simple que efectúo el banco que aplicó una TNT de descuento anticipada de 8,5%.
Asimismo, calcular el valor descontado o valor presente de la letra de cambio pagaré. Rpta.
$465,33 y $3.284,67
15. Una letra de cambio que tiene un valor de nominal de $8.820 fue descontada por el BCP,
cuando faltaba 136 días para su vencimiento. Se requiere conocer el importe del descuento
racional simple que efectúo el banco que aplicó una TNQ de descuento anticipada de 1,25%.
Asimismo, calcular el valor descontado o valor presente de la letra de cambio pagaré. Rpta.
$897,84 y Rpta. $7.922,16
Descuento racional simple con tasa d nominal variable
16. Calcule el descuento racional simple que se efectuará a un pagaré con valor nominal de
$12.500. El pagaré se descontará el 13 de febrero y vencerá el 9 de julio del mismo año. La
TNA será del 14% hasta el 26 de mayo y a partir de esa fecha se incrementará al 16%. A su
vez calcule el valor descontado o valor presente del pagaré. Rpta. $698,89 y $11.801,11

126. 126
17. Calcule el descuento racional simple que se efectuará a un pagaré con valor nominal de
$25.000. El pagaré se descontará el 8 de enero y vencerá el 20 de octubre del mismo año. Al
término del plazo se conoce que las tasas de descuento fueron las siguientes:
Tasa A partir del
TNS 8,0% 08/01
TNT 4,5% 26/05
TNQ 0,8% 05/09
Calcule el interés descuento en la fecha de cierre, así como el valor descontado o valor
presente del pagaré. Rpta. $2.999,41 y Rpta. $22.000,59
Descuento racional compuesto con tasa i efectiva constante
18. Calcular los intereses de descuento racional compuesto que aplica el Banco Interfip por una
letra de cambio que asciende a $4.250, faltando un año para su vencimiento. A su vez calcule
el valor descontado o valor presente de la letra de cambio. El banco cobra una TES del 12%.
Rpta. $861,93 y $3.388,07
19. Una letra de cambio que tiene un valor de nominal de $3.750 fue descontada por el BCP,
cuando faltaba cinco meses para su vencimiento. Se requiere conocer el importe del descuento
racional compuesto que efectúo el banco que aplicó una TET de descuento anticipada de
8,5%. A su vez calcule el valor descontado o valor presente de la letra de cambio. Rpta.
$476,73 y Rpta. $3.273,27
20. Una letra de cambio que tiene un valor de nominal de $8.820 fue descontada por el BCP,
cuando faltaba 136 días para su vencimiento. Se requiere conocer el importe del descuento
racional compuesto que efectúo el banco que aplicó una TEQ de descuento anticipada de
1,25%. A su vez calcule el valor descontado o valor presente de la letra de cambio. Rpta.
$939,50 y $7.880,50
Descuento racional compuesto con tasa i efectiva variable
21. Una letra de cambio que tiene un valor de nominal de $8.820 fue descontada por el BCP,
cuando faltaba 136 días para su vencimiento. Se requiere conocer el importe del descuento
racional simple que efectúo el banco que aplicó una TNQ de descuento anticipada de 1,25%.
Asimismo, calcular el valor descontado o valor presente de la letra de cambio pagaré. Rpta.
$897,84 y Rpta. $7.922,16
22. Calcule el descuento racional compuesto que se efectuará a un pagaré con valor nominal
de $12.500. El pagaré se descontará el 13 de febrero y vencerá el 9 de julio del mismo
año. La TEA será del 14% hasta el 26 de mayo y a partir de esa fecha se incrementará al
15%. Asimismo, calcular el valor descontado o valor presente del pagaré. Rpta. $672,07 y
$11.827,93
23. Calcule el descuento racional compuesto que se efectuará a un pagaré con valor nominal de
$25.000. El pagaré se descontará el 8 de enero y vencerá el 20 de octubre del mismo año. Al
término del plazo se conoce que las tasas de descuento fueron las siguientes:

127. 127
Tasa A partir del
TEA
8,0%
08/01
TES
4,5%
26/05
TET
0,8%
05/09
Calcule el interés descuento en la fecha de cierre, así como el valor descontado o valor
presente del pagaré. Rpta. $3.108,86 y $21.891,14
Descuento con tasa j capitalizable
24. Calcular los intereses de descuento racional compuesto que aplica el Banco Interfip por una
letra de cambio que asciende a $4.250, faltando un año para su vencimiento. El banco cobra
una TES del 12% capitalizable mensualmente. Calcular también el valor descontado o valor
presente de la letra de cambio. Rpta. $898,90 y $3.351,10
25.
Una letra de cambio que tiene un valor de nominal de $3.750 fue descontada por el
BCP, cuando faltaba cinco meses para su vencimiento. Se requiere conocer el importe del
descuento racional compuesto que efectúo el banco que aplicó una TET de 8,5% capitalizable
mensualmente. Calcular también el valor descontado o valor presente de la letra de cambio.
Rpta. $488,92 y Rpta. $3.261,08
26. Una letra de cambio que tiene un valor de nominal de $8.820 fue descontada por el BCP, cuando
faltaba 136 días para su vencimiento. Se requiere conocer el importe del descuento racional
compuesto que efectúo el banco que aplicó una TEQ de 1,25% capitalizable quincenalmente.
Calcular también el valor descontado o valor presente de la letra de cambio. Rpta. $939,50
y Rpta. $7.880,50
Operaciones de descuento en la práctica
27. Una persona descuenta un pagaré por $8.500 en un banco, 90 días antes de su vencimiento,
a una TEA de 10%. Si paga además $10 por conceptos de gastos bancarios y 0,2% por
concepto de comisiones, sobre el pagaré. Calcular el abono que hará el banco en la cuenta
corriente del cliente y el costo efectivo de la operación. Rpta. $8.272,86 y 11,44%
28. Textiles Pacifico S.R.L. descuenta un pagaré por $8.500 en un banco, 45 días antes de su
vencimiento, a una TEA de 10%. Si paga además $10 por conceptos de gastos bancarios y
0,2% por concepto de comisiones, sobre el pagaré. Calcular el abono que hará el banco en la
cuenta corriente del cliente y el costo efectivo de la operación. Rpta. $8.372,33 y 12,87%

129. Cálculo financiero
P R O E S A D
129
5
Sesión
Tasas
1. INTRODUCCIÓN
En el sistema financiero, los productos transados son colocaciones y captaciones, cuyo costo,
denominados tasa de interés, se fija de acuerdo con las reglas del mercado, bajo la regulación
y supervisión de organismos especializados, creados de acuerdo a ley. En el Perú la entidad
encargada de la regulación y supervisión es la Superintendencia de Banca y Seguros SBS.
Existe una terminología muy variada para designar las diversas tasas de interés vigentes en el
sistema financiero, muchas de ellas representan el mismo concepto a pesar de tener diferentes
denominaciones. En la tabla 1 se trata de agrupar, clasificar y definir esas tasas, en función de
algún elemento común que las relacione.
Tabla 1
Clasificación de las tasas (tomado de Carlos Aliaga)
Vencida
Anticipada
Según se aplique directamente al valor presente de
un capital o al valor futuro de un título-valor.
Nominal proporcional
Efectiva equivalente
De acuerdo con el número de periodos de tiempo.
Activa
Pasiva
Compensatoria
Moratoria
Según el balance bancario para sus operaciones de
colocaciones y captaciones respectivamente.
Por la contraprestación del uso del dinero e indem-
nización por incumplimiento.
TANM Tasa activa en moneda nacional
TAMEX Tasa activa en moneda extranjera
Según el tipo de moneda.
TIPMN Tasa de interés pasiva en moneda nacional
TIPMEX Tasa de interés pasiva en moneda extranjera
Discreta
Continua
Por el tipo de capitalización.
Explícita
Implícita
De acuerdo con su participación o no en la opera-
ción.

130. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
130
2. TASA VENCIDA Y ANTICIPADA
La tasa vencida es la relación del interés con el capital inicial. La aplicación de una tasa vencida
al capital inicial genera interés a medida que transcurren los periodos durante el horizonte
temporal.
La tasa anticipada es la relación del interés con el capital final. La aplicación de una tasa anticipada
al capital final descuenta interés a medida que transcurren los periodos durante el horizonte
temporal.
3. TASA NOMINAL PROPORCIONAL
También conocida como tasa convencional o referencial y lo fija un Banco Federal o Banco Central
de un país para regular las operaciones activas (préstamos y créditos) y pasivas (depósitos y
ahorros) del sistema financiero. Siendo la tasa nominal un límite para ambas operaciones y como
su empleo es anual resulta equivalente decir, tasa nominal o tasa nominal anual.
Lo importante es que cuando hablamos de tasa nominal estamos hablando de un interés simple
que solamente podemos dividirlo o multiplicarlo para calcular el monto o capital final de una
operación.
La tasa nominal es aquella que corresponde a diferentes fracciones de tiempo, generalmente
periodos menores de un año con los cuales es directamente proporcional. Se utiliza cuando
necesitamos calcular el interés (I) en una operación y la tasa de interés mencionada (nominal)
está en distintos términos a los periodos (m) pudiendo ser estos periodos de calculo menores o
mayores al periodo que se refiere la tasa nominal.
Ejemplo 1
Tasa nominal proporcional
Convertir una TNA de 15% en una TNS, TNC, TNT, TNM, TNQ y TND.
Solución:
Las tasas equivalentes son como sigue:
Tasa nominal Siglas Cálculo Tasa proporcional
Semestral TNS 15/2 7,500 %
Cuatrimestral TNC 15/3 5,000 %
Trimestral TNT 15/4 3,750 %
Mensual TNM 15/12 1,250 %
Quincenal TNQ 15/24 0,625 %
Día TND 15/360 0,041 %
De esto se deduce que una TNA de 15% es proporcional a:
7,5% semestral (=15/2 = 7,5)
3,75% trimestral (=15/4 = 3,75)
1,25% mensual (=15/12 = 1,25). 

131. Cálculo financiero
P R O E S A D
131
Ejemplo 2
Tasa nominal proporcional
Convertir una TND de 0,05% en una TNQ, TNM, TNT, TNC, TNS y TNA.
Solución:
Las tasas equivalentes son como sigue:
Tasa nominal Siglas Cálculo Tasa proporcional
Quincenal TNQ 0,05 x 15 0,750 %
Mensual TNM 0,05 x 30 1,500 %
Trimestral TNT 0,05 x 90 4,500 %
Cuatrimestral TNC 0,05 x 120 6,000 %
Semestral TNS 0,05 x 180 9,000 %
Anual TNA 0,05 x 360 18,000 %
De esto se deduce que una TND de 0,05% es proporcional a:
1,5% mensual (=0,05 x 30 = 1,5).
4,5% trimestral (=0,05 x 90 = 4,5)
9,0% semestral (=0,05 x 180 = 9,0) 
4. CONVERSIÓN DE UNA TASA NOMINAL A EFECTIVA
La tasa efectiva i es la verdadera tasa de rendimiento que produce un capital inicial en una
operación financiera. Para convertir una tasa nominal capitalizable m veces durante su plazo, en
una tasa efectiva capitalizada n veces durante el horizonte temporal de la operación financiera,
se utiliza la siguiente fórmula:
i
J
m
m
= +





 −
1 1 (1)
La fórmula anterior convierte una tasa nominal capitalizable m veces durante su plazo, en una
tasa efectiva capitalizada durante n períodos de tasa, en la cual la relación (que también es la
tasa efectiva del período capitalizable) y n hacen referencia a la misma unidad de tiempo.
Es conveniente señalar además que cuando se nos da como dato una tasa nominal, a la tasa
proporcional (que vimos en el punto anterior) correspondiente al período de capitalización se le
denomina también tasa efectiva.
Ejemplo 1
Cálculo de la tasa efectiva
Un banco ofrece préstamos a una TNA de 10% ¿Cuál es la TEA si la capitalización fuera
anual?

132. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
132
Solución:
Utilizando la ecuación (1) tenemos:
i = +





 − =
1
0 10
1
1 10
1
,
%
La TEA que cobra el banco es 10%. En este caso, el banco me cobra la tasa que anuncia.
Una TNA es igual a una TEA solo cuando los intereses se capitalizan anualmente. Lo mismo,
una TNS será igual a una TES, sólo si los intereses se capitalizan semestralmente. 
Ejemplo 2
Cálculo de la tasa efectiva
Un banco ofrece préstamos a una TNA de 10% ¿Cuál es la TEA si la capitalización fuera
mensual?
Solución:
Utilizando la ecuación (1) tenemos:
i = +





 − =
1
0 10
12
1 10 47
12
,
, %
Una TNA de 10% se convierte en una TEA de 10,47%, debido a que los intereses se
capitalizan de manera mensual. 
Ejemplo 3
Cálculo de la tasa efectiva
Un banco ofrece préstamos a una TNA de 10% ¿Cuál es la TEA si la capitalización fuera
diaria?
Solución:
Utilizando la ecuación (1) tenemos:
i = +





 − =
1
0 10
360
1 10 52
360
,
, %
Una TNA de 10% se convierte en una TEA de 10,52%, debido a que los intereses se
capitalizan de manera diaria. 

133. Cálculo financiero
P R O E S A D
133
Ejemplo 4
Cálculo de la tasa efectiva
Un banco ofrece préstamos a una TNA de 18% ¿Cuál es la TES si la capitalización fuera
semestral?
Solución:
Utilizando la ecuación (1) tenemos:
i = +





 − =
1
0 18
2
1 9
1
,
%
En este ejemplo, se comprueba que cuando se nos da como dato una tasa nominal, a la
tasa proporcional correspondiente al período de capitalización se le denomina también
tasa efectiva. La TES es 9%. 
5. TASA EFECTIVA EQUIVALENTE
Como se ha visto en los capítulos anteriores cuando hablamos de tasa efectiva estamos hablando
de un interés compuesto que para convertirla en distintas unidades de tiempo tenemos que
utilizar las operaciones matemáticas llamadas: radicación y potenciación.
La tasa efectiva equivalente, es aquella, que en condiciones diferentes, producen la misma tasa
efectiva anual. Mejor dicho dos tasas con diferentes periodos de capitalización, son equivalentes,
si producen el mismo valor actual o futuro, en cualquier periodo.
Ejemplo 1
Tasa efectiva equivalente
Convertir una TEA de 15% en una TES, TEC, TET, TEM, TEQ y TED.
Solución:
Las tasas equivalentes son como sigue:
Tasa nominal Siglas Cálculo Tasa equivalente
Semestral TES 1 0 15 1
2 +
( ) −
, 7,238 %
Cuatrimestral TEC 1 0 15 1
3 +
( ) −
, 4,768 %
Trimestral TET 1 0 15 1
4 +
( ) −
, 3,555 %
Mensual TEM
1 0 15 1
12 +
( ) −
, 1,171 %
Quincenal TEQ 1 0 15 1
24 +
( ) −
, 0,584 %
Día TED 1 0 15 1
360 +
( ) −
, 0,038 %

134. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
134
De esto se deduce que una TEA de 15% es equivalente a:
7,238% semestral
3,555% trimestral
1,171% mensual. 
Ejemplo 2
Tasa efectiva equivalente
Convertir una TED de 0,05% en una TEQ, TEM, TET, TEC, TES y TEA.
Solución:
Las tasas equivalentes son como sigue:
Tasa nominal Siglas Cálculo Tasa equivalente
Quincenal TNQ
1 0 0005 1
15
+
( ) −
, 0,752 %
Mensual TNM
1 0 0005 1
30
+
( ) −
, 1,511 %
Trimestral TNT 1 0 0005 1
90
+
( ) −
, 4,602 %
Cuatrimestral TNC 1 0 0005 1
120
+
( ) −
, 6,182 %
Semestral TNS 1 0 0005 1
180
+
( ) −
, 9,415 %
Anual TNA
1 0 0005 1
360
+
( ) −
, 19,716 %
De esto se deduce que una TED de 0,05% es equivalente a:
1,511% mensual
4,602% trimestral
9,415% semestral 
6. TASA ACTIVA Y PASIVA
Estas tasas son las que cobran los bancos e instituciones que se mueven dentro del sistema
financiero. Hay una diferencia enorme entre uno y otro concepto, a continuación definiremos
cada una de ellas.
6.1. Tasa de interés pasiva
A los pagos que efectúan u ofrecen las empresas financieras a las captaciones de fondos que
ésta realiza al público, se les conoce como tasa pasiva, porque son obligaciones que tienen las
entidades financieras y son registradas en el pasivo del balance.
Las tasas pasivas aplicadas por las instituciones del sistema financiero a los usuarios finales
se expresan generalmente en términos nominales y con una frecuencia de capitalización
determinada; por ejemplo., los ahorros capitalizan mensualmente, mientras los depósitos a
plazo capitalizan a diario.

135. Cálculo financiero
P R O E S A D
135
Las operaciones pasivas que efectúan estas empresas son:
a) Cuentas corrientes
b) Depósitos de ahorros
c) Depósitos a plazos
d) Depósitos de CTS
Ejemplo
Tasa de interés pasiva
La señorita Livni Vidal, tiene una cuenta de ahorros en el BBVA, cuyo monto es de $3.000,
los cuales permanecen por un espacio de tres años, a una TNA del 6% con capitalización
mensual. ¿Cuál es el monto que retirará Livni una vez cumplido el plazo?
Solución:
Los datos son:
S = ?
P = $3.000
i = 6%
n = 3 años
Utilizando la ecuación (7) del capítulo de interés compuesto se tiene:
S = +














=
$ .
,
$ . ,
3 000 1
0 06
12
3 590 04
36
Enestecaso,comoesunacuentadeahorros,elbancocapitalizalosinteresesmensualmente.
Por tanto, Livni recibirá al final de los tres años, la suma de $3.590,04. 
6.2. Tasa de interés activa
Tasas de interés aplicadas para fondos disponibles a colocaciones, inversiones y otros tipos de
operaciones que por su naturaleza son registradas en los distintos rubros del activo del balance.
Son pues, las tasas que cobran las empresas del sistema financiero, cuando efectúan colocaciones
(préstamos).
Las operaciones activas que efectúan estas empresas son:
a) Préstamos
b) Descuentos
c) Sobregiros, etc.
La tasa activa, generalmente está expresada en términos efectivos.

136. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
136
Ejemplo
Tasa de interés activa
El BCP ha prestado a la empresa Los Amigos S.A.C., debidamente representada por su
Gerente General, el señor Marco Bonilla, la suma de $3.000 a una TEA de 20% a pagar en
3 años. ¿Cuál es el monto que pagará la empresa una vez cumplido el plazo?
Solución:
Los datos son:
S = ?
P = $3.000
i = 20%
n = 3 años
Utilizando la ecuación (7) del capítulo de interés compuesto se tiene:
S = +
( )




=
$ . , $ .
3 000 1 0 20 5 184
3
Podemos observar que la suma original de $3.000 se ha incrementado notablemente. De
esta manera, la empresa Los Amigos S.A.C., tendrá que pagar al final de los tres años, la
suma de $5.184. 
Se puede ver que para un mismo importe y un mismo periodo de tiempo –$3.000 y 3 años–, el
BCP pagó de intereses (tasa pasiva) en tres años a la señorita Vidal, la suma de $590,04 y cobró
de intereses (tasa activa) por un préstamo a la empresa Los Amigos S.A.C., la suma de $2.184.
Sin duda un gran negocio del BCP.
7. TASA COMPENSATORIA Y MORATORIA
Una tasa de interés es compensatoria cuando constituye la contraprestación por el uso del dinero
o de cualquier otro bien. En operaciones bancarias, la tasa de interés convencional compensatoria,
está representada por la tasa activa para las colocaciones y la tasa pasiva para las captaciones
que cobran o pagan respectivamente las instituciones del sistema financiero, en el proceso de
intermediación del crédito.
Una tasa de interés importante es la moratoria que constituye la indemnización por
incumplimiento del deudor en el reembolso del capital y del interés compensatorio en las fechas
convenidas. El interés moratorio se calcula sobre el monto de la deuda correspondiente al capital,
adicionalmente a la tasa de interés convencional compensatoria o a la tasa de interés legal,
cuando se haya pactado.
El deudor incurre en mora a partir del día siguiente de la fecha de vencimiento de una cuota si
ésta no se cancela. Una deuda en mora afecta a una tasa efectiva de interés compensatorio y
paralelamente a una tasa efectiva de interés moratorio.

137. Cálculo financiero
P R O E S A D
137
7.1. Aplicación de tasa compensatoria y moratoria en pagarés
Un pagaré es un documento mediante el cual una persona natural o jurídica se obliga a pagar a
una institución financiera una cantidad determinada de dinero, con interés o sin él, en una fecha
dada. La persona que hace la promesa de pagar es el deudor u otorgante, y la persona que cobra
el pagaré es el beneficiario o tenedor.
En todo pagaré interviene los siguientes conceptos:
a) Fecha: es la fecha en la que se extiende el pagaré.
b) Fecha de vencimiento: es la fecha en la cual debe ser pagada la deuda.
c) Plazo: es el tiempo que transcurre entre la fecha en que se extiende el pagaré y la fecha de
vencimiento.
d) Valor nominal: es la cantidad marcada en el pagaré. Si en el pagaré se indica que el valor
nominal causará intereses a determinada tasa, entonces el valor nominal es el capital
obtenido en préstamo; en cambio, si en el pagaré se indica que el valor nominal incluye
intereses a determinada tasa, entonces el valor nominal es el monto a pagar en la fecha de
vencimiento.
e) Valor de vencimiento: es la cantidad que debe ser pagada en la fecha de vencimiento. Esto
es, el capital más los intereses, si los hubiera.
El siguiente documento reúne las características mínimas de todo pagaré.
Documento No. Por $7.500,00
Por este PAGARÉ me (nos) obligo (amos) a pagar incondicionalmente a la
orden de: Banco de Crédito del Perú – BCP en la ciudad de Lima, el día 27
de noviembre de 2005 la cantidad de siete mil quinientos dólares. Valor
recibido a mi (nuestra) entera satisfacción. La suma incluye intereses a la TEM
de 4% hasta la fecha de su vencimiento, y si no es pagada al vencimiento
causará intereses moratorios a una TEM de 2%.
Lugar y fecha: Lima, 13 de febrero de 2005
Nombre: Kamila Romero Angeles
Domicilio: Av. Los Alamos 480, Surco _________________
Ciudad: Lima Acepto (amos)
A continuación, explicaremos las características de este pagaré:
a) Kamila Romero Angeles es el deudor (persona que hace la promesa).
b) Banco de Crédito del Perú es el beneficiario (Banco que cobra el pagaré).
c) $7.500,00 es el valor nominal del pagaré.
d) 13 de febrero de 2005 es la fecha en que fue expedido el pagaré.
e) 27 de noviembre de 2005 es la fecha de vencimiento del pagaré.
f) 287 días es el plazo del pagaré.

138. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
138
Ejemplo
Cálculo del interés compensatorio y moratorio
Supóngase que el pagaré anterior se canceló el 03 de diciembre. Calcule el importe del
interés compensatorio, del interés moratorio y la cantidad total a pagar.
Solución:
El importe del interés compensatorio se calcula como sigue:
ic = +
( ) −





 =
7 500 1 0 04 1 59 06
6
30
. , $ ,
El importe del interés moratorio se calcula como sigue:
im = +
( ) −





 =
7 500 1 0 02 1 29 76
6
30
. , $ ,
La cantidad total a pagar el 05 de diciembre se calcula como sigue:
S = + + =
7 500 59 06 29 76 7 588 82
. , , $ . ,
Kamila deberá pagar el 05 de diciembre la suma de $7.588,82. 
8. TAMN, TAMEX, TIPMN, TIPMEX
A partir del 11 de marzo de 1991, el Banco Central de Reserva del Perú utiliza la siguiente
terminología para las operaciones activas y pasivas que efectúan las entidades del sistema
financiero nacional:
TAMN Tasa Activa Moneda Nacional
TAMEX Tasa Activa Moneda Extranjera
TIPMN Tasa de Interés Pasiva Moneda Nacional
TIPMEX Tasa de Interés Pasiva Moneda Extranjera
Las tasas activas se expresan en términos efectivos y las tasas pasivas en términos nominales
con una frecuencia de capitalización determinada, de acuerdo con el tipo de operación realizada.
Los ahorros capitalizan mensualmente y los depósitos a plazo capitalizan a diario. La magnitud
de las tasas en moneda extranjera depende del riesgo de la operación y de la moneda que se
utilice en la transacción.

139. Cálculo financiero
P R O E S A D
139
9. TASA CON CAPITALIZACIÓN DISCRETA Y CONTINUA
9.1. Tasa con capitalización discreta
La tasa con capitalización discreta es una tasa nominal cuyo plazo de capitalización supone
espacios definidos de tiempo, como anuales, semestrales, mensuales, e incluso horas y minutos,
cuyo resultado se acerca a un límite cuando el plazo de capitalización se hace más pequeño.
Ejemplo
Tasa con capitalización discreta
Si una TNA de 15% capitaliza a diario y cada hora, calcule su TEA.
Solución:
Si los intereses se capitalizan cada día, la TEA será:
i = +





 − =
1
0 15
360
1 16 1797947
360
,
, %
Si los intereses se capitalizan cada hora, la TEA será:
i = +





 − =
1
0 15
360 24
1 16 1832719
360 24
,
*
, %
*
Si los intereses se capitalizan cada día la TEA sería 16,1797947% y si los intereses se
capitalizan cada hora, la TEA sería 16,1832719%. 
9.2. Tasa con capitalización continua
La tasa con capitalización continua es una tasa nominal cuyo plazo de capitalización se hace cada
vez más pequeño y tiende a infinitos periodos y, por tanto, incrementa la tasa efectiva.
Ejemplo
Tasa con capitalización continua
Si una TNA de 15% capitaliza cada minuto, calcule su TEA.
Solución:
Si los intereses se capitalizan cada minuto, la TEA será:

140. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
140
i = +





 − =
1
0 15
360 24 60
1 16 1833102
360 24 60
,
* *
, %
* *
Si los intereses se capitalizan cada minuto la TEA sería 16,1833102%. 
10. TASA EXPLÍCITA E IMPLÍCITA
La tasa explícita es una tasa anunciada en las operaciones mercantiles y financieras. La tasa
implícita o tasa interna de retorno (TIR) no figura expresamente en la operación financiera o
mercantil, pero está oculta en el costo total cuando se compara un precio de contado con un
precio al crédito generalmente más elevado, o cuando un préstamo debe cancelarse en varias
cuotas. De acuerdo con el tipo de información disponible, la tasa implícita se calcula con las
diversas tasas de interés, o con el principio de equivalencia financiera.
Ejemplo 1
Cálculo de la tasa implícita
Una cámara digital marca SONY puede comprarse al contado a $200 o con un crédito a 60
días en $225, calcule la tasa implícita mensual de la cámara digital.
Solución:
La tasa implícita se puede calcular como sigue:
i =





 − =
225
200
1 6 07
30
60
, %
La TEM implícita es de 6,07%. 
Ejemplo 2
Cálculo de la tasa implícita
Una computadora portátil marca toshiba tiene un precio de contado de $1.200, pero al
crédito puede adquirirse con una cuota inicial de $200 y cinco cuotas mensuales de $235,
¿qué TEM y TEA se aplicó en el financiamiento?
Solución:
El problema puede plantearse en la siguiente ecuación de valor:
1 200 200
225
1
225
1
225
1
225
1
225
1
2 3 4 5
. − =
+
( )
+
+
( )
+
+
( )
+
+
( )
+
+
( )
i i i i i

141. Cálculo financiero
P R O E S A D
141
Para dar solución al problema, tenemos que encontrar aquella tasa de interés i que hace
que los dos miembros de la ecuación sean iguales.
Al aplicar el método de «prueba y error», puede asignarse diversos valores a i hasta
conseguir que el valor del segundo miembro de la ecuación se iguale con el importe de
$1.000.
Se puede observar que la tasa de interés es superior a 4%, pero inferior a 5%, por lo que
al interpolar dichas tasas puede encontrarse que la TEM es de 4,06% aproximadamente,
como se explica a continuación.
x =
−
−





 −
( ) =
1 001 66 1 000
1 001 66 974 13
5 4 0 0604295
. , .
. , ,
,
i = + =
4 0 06 4 06
% , , %
Se puede observar que la tasa i que hace que los dos miembros de la ecuación sean
iguales es 4,06%. Entonces la TEM implícita en el financiamiento es de 4,06. Ahora, ¿Por
qué una TEM y no TEA? La respuesta es sencilla, es una TEM porque la ecuación de valor o
el flujo de caja de la operación esta en meses.
Si se quiere calcular la TEA se procede como sigue:
i = +
( ) − =
1 0 0406 1 61 2
12
, , %
La TEA implícita es de 61,2%. 
i Valor
0% $1.125,00
4% $1.001,66
x $1.000,00
5% $974,13

142. 142
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Tasa nominal proporcional
1. Convertir una TNA de 25% en una TNS, TNC, TNT, TNM, TNQ y TND.
Rpta. 12,50%, 8,33%, 6,25%, 2,08%, 1,04%, 0,07%
2. Convertir una TND de 0,015% en una TNQ, TNM, TNT, TNC, TNS y TNA.
Rpta. 0,225%, 0,45%, 1,35%, 1,80%, 2,70%, 5,40%.
Conversión de una tasa nominal a tasa efectiva
3. El BWS está ofreciendo préstamos a una TNA de 12% ¿Cuál es la TEA si la capitalización
semestral?
Rpta. 12,36%
4. El BBVA está ofreciendo préstamos a una TNS de 8,5% ¿Cuál es la TET si la capitalización fuera
mensual?
Rpta. 4,31%

143. 143
5. Interbank está ofreciendo préstamos a una TNS de 14% ¿Cuál es la TET si la capitalización
fuera trimestral?
Rpta. 7%
6. El BCP ofrece préstamos a una TNA de 18% ¿Cuál es la TES si la capitalización fuera trimestral?
Rpta. 9,20%
Tasa efectiva equivalente
7. Convertir una TEA de 18% en una TES, TEC, TET, TEM, TEQ y TED.
Rpta. 8,63%, 4,22%, 5,67%, 1,39%, 0,69%, 0,05%
8. Convertir una TED de 0,03% en una TEQ, TEM, TET, TEC, TES y TEA.
Rpta. 0,45%, 0,90%, 2,74%, 3,67%, 5,55%, 11,40%
Tasa activa y pasiva
9. Luiggi Carozzi, deposita en una cuenta a plazo fijo del BBVA la suma de $5.000, los cuales
permanecen por un espacio de 18 meses, a una TNA del 8% con capitalización diaria. ¿Cuál
es el monto que retirará Luiggi una vez cumplido el plazo?
Rpta. $5.637,41
10. Fernando Gonzáles recibe un préstamo del BCP por $5.000 a una TEA de 22% a pagar en 18
meses. ¿Cuál es el monto que pagará Fernando una vez cumplido el plazo?
Rpta. $6.737,67
Tasa compensatoria y moratoria
11. En el siguiente pagaré, suponga que la señorita Karina cancela su deuda el 05 de noviembre.
Calcule el importe del interés compensatorio, del interés moratorio y la cantidad total a
pagar. Rpta. $44,04, $21,97, $4.566,01
Documento No. Por $4.500,00
Por este PAGARÉ me (nos) obligo (amos) a pagar incondicionalmente a la orden
de: Banco de Crédito del Perú – BCP en la ciudad de Lima, el día 20 de octubre
de 2005 la cantidad de cuatro mil quinientos dólares. Valor recibido a mi (nuestra)
entera satisfacción. La suma incluye intereses a la TEA de 24,50% hasta la fecha de
su vencimiento, y si no es pagada al vencimiento causará intereses moratorios a una
TEA de 11,58%.
Lugar y fecha: Lima, 08 de enero de 2005
Nombre: Karina Falcón Delgado
Domicilio: Av. Los Alamos 480, Surco __________________
Ciudad: Lima Acepto (amos)
Tasa con capitalización discreta y continua

144. 144
12.
Si una TNS de 9,52% capitaliza a diario y cada hora, calcule su TEA. 20,96725037%,
20,9730782%
13. Si una TNA de 20% capitaliza cada minuto, calcule su TEA.
Rpta. 20,9730874
Tasa explícita e implícita
14. Una impresora HP de última generación puede comprarse al contado a $450 o con un crédito
a 60 días en $505, calcule la tasa implícita mensual y bimestral de la impresora.
Rpta. 5,93%, 12,22%
15. Una computadora portátil marca compact tiene un precio de contado de $1.200. Usted puede
financiar la PC en dos tiendas de la siguiente manera:
• Saga Falabella: sin inicial y seis cuotas mensuales de $230.
• La Curacao: una inicial de $200 y seis cuotas mensuales de $195.
¿Qué TEM y TEA aplicó cada una de las tiendas y cuál es la mejor?
Rpta. Saga: 4,15% y 62,81%; Curacao: 4,68% y 73,11%

145. Cálculo financiero
P R O E S A D
145
6
Sesión
inflación y
devaluación
1. INTRODUCCIÓN
La inflación es el fenómeno que se caracteriza por el incremento generalizado de los precios de
los bienes y servicios, cuyo efecto, entre otros es la pérdida del poder adquisitivo de la moneda
que distorsiona el mercado de créditos. La devaluación de la unidad monetaria de un país es
un proceso de disminución de su valor con relación a otro activo, como el oro o las monedas de
otros países.
De esta manera, la unidad monetaria de cada país está sujeta a cambios en su poder adquisitivo
por inflación o por devaluación, cuyas causas exceden el análisis en este texto.
En el estudio de los procesos inflacionarios se usan indicadores como índice de precios
al consumidor (IPC), el índice de precios al por mayor (IPM), u otro específico que rija para
determinada actividad productiva. Un índice de precios es un indicador estadístico de carácter
estimativo que refleja la variación del precio de una canasta de artículos entre dos momentos
de cierto horizonte temporal; este indicador no necesariamente es un índice de costo de vida, ya
que éste puede evolucionar por cantidad, calidad y precio. En la tabla 1 se muestra el índice de
precios al consumidor a nivel nacional (IPC) y su variación porcentual 2003-2005 de la economía
peruana.

146. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
146
Tabla 1
IPC a nivel nacional y variación porcentual: 2004-2005
FUENTE: Instituto Nacional de Estadística e Informática
2. CÁLCULO DE LA TASA DE INFLACIÓN
La tasa de inflación p es una tasa efectiva, que indica que el crecimiento sostenido de los precios
de los bienes y servicios de la economía, en un período dado, con base en una canasta básica de
consumo familiar, tomada en una fecha cuya estructura de costos corresponde a una base dada.
Si se designa IP0 al índice de precios en un momento dado e IPn al índice de precios en un
momento posterior, la tasa de inflación acumulada en ese periodo puede calcularse con la
siguiente ecuación:
π = −
IP
IP
n
0
1 (1)
La fórmula anterior calcula la inflación de un plazo determinado cuando se dispone de índices de
precios que pueden ser en caso IPC, IPM u otro diferente.
Ejemplo 1
Cálculo de la inflación
Utilizando la tabla 1, calcule la inflación del periodo del 1 de enero al 30 de abril de 2005.
Solución:
Meses
ÍNDICE PROMEDIO
MENSUAL
VARIACIÓN PORCENTUAL
Mensual Acumulada
2004 2005 2004 2005 2004 2005
Enero 103,23 106,47 0,55 0,04 0,55 0,04
Febrero 104,30 106,20 1,03 -0,26 1,59 -0,21
Marzo 104,86 106,73 0,54 0,50 2,14 0,29
Abril 104,83 106,82 -0,04 0,09 2,11 0,38
Mayo 105,17 106,94 0,33 0,11 2,44 0,49
Junio 105,66 107,22 0,47 0,27 2,92 0,75
Julio 105,95 107,31 0,27 0,08 3,20 0,83
Agosto 105,90 107,24 -0,05 -0,06 3,15 0,77
Setiembre 105,99 107,24 0,09 -0,01 3,24 0,77
Octubre 106,07 107,39 0,07 0,14 3,31 0,91
Noviembre 106,38 107,46 0,30 0,06 3,62 0,97
Diciembre 106,42 107,95 0,04 0,46 3,66 1,43

147. Cálculo financiero
P R O E S A D
147
Los datos son:
P = ?
IPCabril 05
= 106,82
IPCdiciembre 04
= 106,42
Reemplazando los valores en la ecuación (1) se tiene:
π = − = =
106 82
106 42
1 0 0229841 2 30
,
,
, , %
La inflación del periodo fue de 2,30%. 
Dado que los índices de precios se refieren al último día de cada período, en el ejemplo anterior,
el IP0 debe ser el índice al 31 de diciembre del año 2004; de este modo, la inflación medida con
estos con estos índices incluye el período comprendido desde el 1 de enero hasta el 30 de abril
del año 2005.
Al ser p (la tasa de inflación) una tasa efectiva que indica la variación de precios, puede aplicársele
lo desarrollado en el capítulo de interés compuesto; así, si se conoce la inflación de un período,
puede hallarse tasas de inflación equivalentes para otros períodos y proyectar la inflación futura
sobre la base de inflaciones pasadas, al suponer que se mantendrá la misma tendencia en el
futuro.
La siguiente ecuación calcula la inflación a partir de índices de precios o a partir de otras tasas
de inflación:
π π
, /
= +
( ) −
1 1
f h
(2)
Ejemplo 2
Cálculo de la inflación
Utilizando la tabla 1, calcule las tasas de inflación de los siguientes periodos.
a) Desde el 1 al 31 de enero de 2005.
b) Desde el 1 de febrero del año 2004 hasta el 28 de febrero del año 2005.
c) La inflación del año 2005.
d) Desde el 1 de mayo de 2005 al 15 de mayo de 2005.
e) Desde el 1 de mayo de 2005 al 22 de junio de 2005.
Solución:
a) Desde el 1 al 31 de enero de 2005.
π = = − = =
IPC
IPC
enero
diciembre
05
04
106 47
106 42
1 0 000469836 0 04
,
,
, , 6
6%

148. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
148
b) Desde el 1 de febrero del año 2004 hasta el 28 de febrero del año 2005.
π = = − = =
IPC
IPC
febrero
enero
05
04
106 20
103 23
1 0 028770706 2 87
,
,
, , %
c) La inflación del año 2005.
π = = − = =
IPC
IPC
diciembre
diciembre
05
04
107 95
106 42
1 0 014376997
,
,
, 1
1 44
, %
d) Desde el 1 de mayo de 2005 al 15 de mayo de 2005.
π =





 =





 − =
IPC
IPC
mayo
abril
05
05
15
31
15
31
106 94
106 82
1 0
,
,
,
, , %
000543416 0 054
=
f) Desde el 1 de mayo de 2005 al 22 de junio de 2005.
π =





 =





 − =
IPC
IPC
junio
abril
05
05
52
61
52
61
107 22
106 82
1
,
,
0
0 003191252 0 32
, , %
=
Ejemplo 3
Cálculo del IPC
Utilizando la tabla 1, calcule el IPC del mes de enero del año 2006, si se conoce que la
inflación de este mes fue de 0,2060%.
Solución:
El cálculo del IPC del mes de enero de 2006 es como sigue:
IPCenero06 107 95 1 0 00206 108 17
= +
( ) =
, , ,
Comprobando se tiene:
π = = − = =
IPC
IPC
enero
diciembre
06
05
108 17
107 95
1 0 00206 0 2060
,
,
, , %
Se comprueba que el IPC del mes de enero de 2006 es de 108,17. 

149. Cálculo financiero
P R O E S A D
149
Ejemplo 4
Cálculo de inflación proyectada
Según el INEI, la inflación del mes de enero de 2006 es 0,2060%. ¿Cuál será la inflación
proyectada del año si la tendencia se mantiene?
Solución:
El cálculo de la inflación anual proyectada es como sigue:
π = +
( ) − =
1 0 00206 1 2 50
12
, , %
La inflación anual sería de 2,50% si la tendencia se mantiene.
3. CÁLCULO DE LA TASA DE INTERÉS REAL
Hasta ahora, en el estudio de las tasas de interés, se obvió el efecto de la inflación, pues se
consideró el valor nominal de la unidad monetaria sin tener en cuenta la variación de su poder
adquisitivo a través del tiempo por el incremento generalizado de los precios de los bienes y
servicios.
La tasa de interés real mide el grado en que la inflación distorsiona los costos o rentabilidad
nominales, disminuyendo al valor de la tasa efectiva de interés. Esta tasa real puede ser positiva
o negativa en función al nivel inflacionario existente.
El hecho de descontar la tasa de inflación a la tasa efectiva de interés se denomina deflactación
y la formula es la siguiente.
i
i
=
−
+
π
π
1
(3)
La ecuación anterior calcula la tasa de interés real cuando se conoce la tasa efectiva y la tasa de
inflación; en este caso, ambas tasas deben corresponder al mismo horizonte temporal.
Ejemplo 1
Cálculo de la tasa de interés real
Kamila deposita $5.000 en una cuenta del BBVA que paga una TEA de 12%. El depósito
tuvo una vigencia de seis meses y la tasa de inflación que se acumuló en ese periodo fue
de 2,50%. Calcule la tasa de interés real semestral que ganó Kamila.
Solución:
En primer lugar calculamos la TES, el cual es como sigue:
TES = +
( ) − =
1 0 12 1 0 0583
2 , ,

150. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
150
A continuación, reemplazamos los valores en la ecuación (3):
i =
−
+
= =
0 0583 0 025
1 0 025
0 03248 3 25
, ,
,
, , %
La tasa de interés real semestral de Kamila fue de 3,25%. 
3.1. Tasa efectiva inflada
Si se manejan flujos de caja nominales, y se supone, que la economía se ve afectada por la
inflación y, por tanto, la unidad monetaria es erosionada de forma permanentemente por la
inflación:
• ¿Cómo podrían expresarse las unidades monetarias de hoy, en unidades monetarias del fu-
turo (afectadas por la inflación) con poder adquisitivo nominal de ese entonces?
• ¿Cómo podría asegurarse que el rendimiento financiero de un capital sea una tasa real pre-
viamente determinada (tasa real meta o deseada que podría ser una tasa mínima?
Para estos efectos debe indexarse la tasa real meta o deseada (que es la tasa de rendimiento
que se exigirá al respectivo capital) con la tasa de inflación que según la estimación, se producirá
durante el horizonte temporal de la operación. Este proceso permitirá expresar los valores
monetarios de hoy con poder adquisitivo de ese entonces, y asegurar el rendimiento de la tasa
real predeterminada.
La tasa efectiva inflada pueda calcularse con la siguiente ecuación:
i i
= +
( ) +
( ) −
1 1 1
π (4)
Ejemplo 1
Cálculo de la tasa efectiva inflada
Kamila deposita $5.000 en una cuenta del BBVA y requiere percibir una tasa efectiva real
de una TEA de 12%, ¿a qué tasa efectiva semestral debería colocarse ese capital, si se
proyecta una tasa de inflación de 2,5% durante dicho periodo? Compruebe la operación.
Solución:
En primer lugar calculamos la TES, el cual es como sigue:
TES = +
( ) − =
1 0 12 1 0 0583
2 , ,
A continuación, reemplazamos los valores en la ecuación (4):
i = +
( ) +
( ) − =
1 0 0583 1 0 025 1 0 084757
, , ,
La inversión debería colocarse a una TES de 8,48%, para que cuando se calcule la tasa real,
ésta sea igual a una TES de 5,83% y a una TEA de 12%.

151. Cálculo financiero
P R O E S A D
151
Para deflactar, se sustituye los valores en la ecuación (3), donde se obtiene:
i =
−
+
= =
0 084757 0 025
1 0 025
0 0583 5 83
, ,
,
, , %
La tasa efectiva real es de 5,83%. Si se quiere calcular la TEA se procede como sigue:
i = +
( ) − = =
1 0 0583 1 0 12 12
2
, , %
Se comprueba que la inversión debería colocarse a una TES de 8,48%. 
4. TIPO DE CAMBIO
El tipo de cambio corresponde al precio de una moneda expresado en función de otra. Una
cotización de moneda extranjera es la formalización del deseo de comprar o vender a un precio
anunciado; esta cotización puede ser directa o indirecta.
El tipo de cambio es doble, puesto que existe un precio para el comprador y otro para el
vendedor. Los dos participantes asumen una posición bivalente, pudiéndose considerar a la
vez compradores y vendedores (venden su moneda y compran otra). Debido a esta posible
confusión y dado que los precios o tipos de cambio son fijados por las instituciones financieras,
las cotizaciones se expresan desde su punto de vista. Así, cuando nos referimos a la posición
compradora (en inglés bid) queremos decir que es el precio que el intermediario va a pagarnos
por adquirir nuestra moneda, puesto que él es el comprador; mientras que si hablamos de la
posición vendedora (en inglés offer o ask) nos indicará el precio que nos costará comprarle dicha
moneda al intermediario, puesto que él nos la vende.
El precio de compra es siempre menor que el de venta, pues la diferencia es lo que posibilita
el beneficio del intermediario. En la tabla 2 se muestra los principales tipos de cambio al 20 de
junio de 2006.
Tabla 2
Principales tipos de cambio: martes 20 de junio de 2006
FUENTE: Sección Negocios de El Comercio
UNIDAD
MONETARIA
Moneda local por US$ Soles por
monedas
Compra Venta
Libra esterlina 0,5429 0,5431 5,993
Yen japonés 115,51 115,54 0,0028
Euro 0,7948 0,7949 4,095
Franco suizo 1,2401 1,2403 2,624
Dólar canadiense 1,1198 1,1204 2,905
Real brasileño 2,253 2,255 1,443
Peso mexicano 11,27 11,57 0,281
Peso chileno 545,00 550,00 0,006
Peso boliviano 8,02 8,10 0,402

152. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
152
Una cotización directa, consiste en enunciar el valor de una unidad monetaria extranjera en
términos de moneda nacional. Por ejemplo S/. 4,095 por cada € 1,00.
Una cotización indirecta, consiste en manifestar el valor de una unidad monetaria nacional con
respecto a cada una de las monedas extranjeras. Por ejemplo € 1,00 por cada S/. 0,2442.
4.1. Tipo de cambio directo
Ejemplo 1
Tipo de cambio directo
Suponga que con S/.409.500 se puede adquirir € 100.000 (euros). Calcule el tipo de
cambio vigente.
Solución:
En el presente caso, al relacionar la primera cantidad con la segunda se tiene:
S/.409.500
€100.000
Esto se puede interpretar que con S/.4,095 puede adquirirse € 1,00. Del mismo modo, al
relacionar la segunda cantidad con la primera, se tiene:
€100.000
S/ 409.500
Lo que puede interpretarse que con € 0,244 se puede adquirir S/.1,00. 
4.2. Tipo de cambio cruzado
Ejemplo 1
Tipo de cambio cruzado
Suponga que con S/.409.500 se puede adquirir € 100.000 y este importe se utiliza para
adquirir ¥ 146.250.000 (yenes japoneses). Calcule el tipo de cambio vigente de cada yen
japonés por cada nuevo sol.
Solución:
En el presente caso, la compra de ¥ 146.250.000 no fue directa mediante una única
operación, sino luego de una intermediación en la que se adquirió previamente € 100.000.
Al relacionar la primera cantidad con la tercera se tiene:
S/.409.500
¥146.250.000
= S/.4,095
= €0,244
= S/.0,0028

153. Cálculo financiero
P R O E S A D
153
En este caso, el valor S/.0,0028 no es un tipo de cambio directo sino un tipo de cambio cruzado.
Lo que puede interpretarse que con S/.0,0028 se puede adquirir ¥1,00. 
5. TASA DE INTERÉS EN MONEDA EXTRANJERA
Para calcular la tasa efectiva en moneda nacional que genera una operación transada en moneda
extranjera, es necesario conocer la tasa de interés que devenga la moneda extranjera, conocer
el tipo de cambio de la moneda extranjera al inicio de la operación y estimar el tipo de cambio
de la moneda extranjera al término de la operación.
La fórmula que nos permite calcular la tasa de interés en moneda extranjera es la siguiente:
i i
TC
TC
ME
MN
ME
n
= +
( )





 −
1 1
0
(5)
La fórmula anterior calcula la tasa efectiva de interés en moneda nacional por operaciones
efectuadas en moneda extranjera, donde iME es la tasa equivalente que genera la moneda
extranjera, y TC0 y TCn son los tipos de cambios en moneda nacional en las fechas de inicio y
término de la operación respectivamente.
Cuando la relación entre los TCs de la moneda nacional es mayor que uno, ocurre una devaluación
o una depreciación de la moneda nacional; en este caso, la ganancia en moneda nacional se
genera por la tasa iME y por la tasa de devaluación que se generó en el periodo de la operación.
Cuando la relación entre los TCs de la moneda nacional es menor que uno, ocurre una revaluación
o una apreciación de la moneda nacional; en este caso, la moneda nacional gana por la tasa iME,
pero pierde por la tasa de revaluación que se generó en el periodo de la operación.
Ejemplo 1
Tasa de interés en moneda extranjera
El 13 de febrero cuando el TC era S/.3,38 por US$1,00, se compró un certificado bancario
en US$ a un plazo de 180 días que rinde una TEA de 8%. En la fecha de vencimiento de
la operación el TC fue S/.3,45. Calcule la tasa efectiva en S/. que rindió ese certificado en
ese plazo.
Solución:
Sustituyendo los valores en la ecuación (5) se tiene:
iUS
S
$
/.
,
,
,
, * ,
= +
( )





 − = −
1 0 08
3 45
3 38
1 1 039230 1 020710 1
180
360 =
= 6 075
, %
La TES en S/. que rindió el certificado en ese plazo fue de 6,075%. En este caso, se observa
que ocurre una devaluación o revaluación de la moneda. 

154. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
154
Ejemplo 2
Tasa de interés en moneda extranjera
El 13 de febrero cuando el TC era S/.3,38 por US$ 1,00, se compró un certificado bancario
en US$ a un plazo de 180 días que rinde una TEA de 8%. En la fecha de vencimiento de
la operación el TC fue S/.3,33. Calcule la tasa efectiva en S/. que rindió ese certificado en
ese plazo.
Solución:
Sustituyendo los valores en la ecuación (5) se tiene:
iUS
S
$
/.
,
,
,
, * ,
= +
( )





 − = −
1 0 08
3 33
3 38
1 1 039230 0 985207 1
180
360 =
= 2 386
, %
La TES en S/. que rindió el certificado en ese plazo fue de 2,386%. En este caso, se observa
que ocurre una revaluación o depreciación de la moneda. 

155. 155
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Cálculo de la tasa de inflación
1. Utilizando la tabla 1, calcule la inflación del periodo del 1 de enero de 2004 al 31 de mayo
de 2005.
Rpta. 0,49%
2. Utilizando la tabla 1, calcule las tasas de inflación de los siguientes periodos.
a) Desde el 1 al 28 de febrero de 2004. Rpta. 1,04%
b) Desde el 1 de julio de 2005 al 20 de julio de 2005. Rpta. 0,054%
c) Desde el 1 de julio de 2005 al 18 de setiembre de 2005. Rpta. 0,0160%
3. Si la tasa de inflación anual fue 2,5%, ¿cuál fue la tasa de inflación promedio mensual? Rpta.
0,2059%
4. Suponga que la inflación del mes de enero de 2006 es 0,258%. ¿Cuál será la inflación
proyectada del año si la tendencia se mantiene? Rpta. 3,014%

156. 156
Cálculo de la tasa de interés real
5. Peter Rivera deposita $10.000 en una cuenta del BBVA que paga una TEA de 11,50%. El
depósito tuvo una vigencia de doce meses y la tasa de inflación que se acumuló en ese
periodo fue de 2,80%. Calcule la tasa de interés real anual que ganó Peter. Rpta. 8,46%
6. Peter Rivera deposita $10.000 en una cuenta del BBVA y requiere percibir una tasa efectiva
real de una TEA de 11,50%, ¿a qué tasa efectiva anual debería colocarse ese capital, si se
proyecta una tasa de inflación de 2,8% durante dicho periodo? Compruebe la operación.
Rpta. 14,62%
Tipo de cambio
7. Suponga que con S/.262.400 se puede adquirir SFr100.000 (francos suizos). Calcule el tipo de
cambio o cotización vigente directa e indirecta. Rpta. S/.2,624 y SFr0,381
8. Suponga que con S/.262.400 se puede adquirir SFr100.000 y este importe se utiliza para
adquirir €64.078,14 (euros). Calcule el tipo de cambio vigente de cada euro por cada nuevo
sol. Rpta.S/.4,095
Tasa de interés en moneda extranjera
9. El 9 de julio cuando el TC era S/. 3,32 por US$ 1,00, se compró un certificado bancario en
US$ a un plazo de 120 días que rinde una TEA de 6,50%. En la fecha de vencimiento de la
operación el TC fue S/. 3,38. Calcule la tasa efectiva en S/. que rindió ese certificado en ese
plazo. Rpta. 3,967%
10. El 9 de julio cuando el TC era S/. 3,32 por US$ 1,00, se compró un certificado bancario en
US$ a un plazo de 120 días que rinde una TEA de 6,50%. En la fecha de vencimiento de la
operación el TC fue S/. 3,29. Calcule la tasa efectiva en S/. que rindió ese certificado en ese
plazo. Rpta. 1,199%

157. Cálculo financiero
P R O E S A D
157
7
Sesión
las seis llaves maestras
de las matemáticas
financieras
1. INTRODUCCIÓN
Las matemáticas financieras, por lo general, se basa en seis expresiones o fórmulas, las cuales
permiten al analista económico y evaluador de proyectos a manejar en forma apropiada el valor
del dinero en el tiempo y el costo de oportunidad del capital.
Como una unidad estas seis fórmulas reciben el nombre de factores financieros. Los principales
factores financieros que efectúan las transformaciones de valor equivalente son las siguientes:
Factor Ecuación
FSC Factor simple de capitalización
S P i
n
= +
( )




* 1
FSA Factor simple de actualización P S
i
n
=
+
( )








*
1
1
FCS Factor de capitalización de la serie S R
i
i
n
=
+
( ) −








*
1 1
FDFA Factor de depósito al fondo de amortización R S
i
i
n
=
+
( ) −








*
1 1
FAS Factor de actualización de la serie P R
i
i i
n
n
=
+
( ) −
+
( )








*
1 1
1
FRC Factor de recuperación del capital R P
i i
i
n
n
=
+
( )
+
( ) −








*
1
1 1

158. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
158
Donde:
“P” es el capital inicial o inversión realizada
“S” es el monto, capital final o valor futuro
“i” es la tasa de interés efectiva de un determinado periodo de tiempo
“R” renta uniforme o flujo de caja anual
“n” es el tiempo que dura la inversión
Para efectuar transformaciones de capitales y rentas aplicando la equivalencia financiera es
necesario utilizar los factores financieros, que se derivan de sumas de progresiones que se
aplican a la teoría rentas en las anualidades.
Estos factores financieros (incluidos entre corchetes) realizan las funciones de equivalencia
financiera.
2. FACTOR SIMPLE DE CAPITALIZACIÓN (FSC)
Denominado como capitalización continua o factor de interés compuesto. Es el valor máximo
que alcanza una cantidad de capital inicial que crece a un interés compuesto y se transforma
en un capital final. Este componente sirve para transformar un stock inicial P de efectivo en
un stock final S de efectivo, aplicando una tasa efectiva i durante un determinado número de
periodos capitalizados n.
Las siglas originales en inglés según George A. Taylor, significa “Single-Payment Compound-
Amount Factor”, que en español Tarquin y Blank denominan como “Factor Cantidad Compuesta
Único Pago”.
Para el cálculo de este factor, se aplica la siguiente ecuación:
S P i
n
= +
( )




1 (1)
Ejemplo
Factor simple de capitalización (FSC)
Supongamos que Sebastián, ha determinado colocar un capital de $10.000 en el Banco de
Crédito que paga una TNA de 8%. ¿Cuál es su stock final de capital después de cinco años?
Solución:
Los datos son:
S = ?
P = $10.000
i = 8%
n = 5 años

159. Cálculo financiero
P R O E S A D
159
El análisis se puede ilustrar en la línea de tiempo como sigue:
Sustituyendo los valores numéricos en la ecuación (1), se obtiene:
S = +
( )




=
10 000 1 0 08 14 693 28
5
. , $ . ,
Sebastián tendría al final de los cinco años, la suma de $14.693,28. 
3. FACTOR SIMPLE DE ACTUALIZACIÓN (FSA)
Conocido como factor de descuento o tasa de actualización. Es el valor actualizado del capital
en una fecha futura. Este factor sirve para trasladar una cantidad del futuro S hacia el presente
P, aplicando una efectiva i durante un determinado número de períodos capitalizado n. Las
siglas en inglés significa “Single-Payment Present-Worth Factor”, que en español se conoce como
“Factor Valor Presente Pago Único”.
Para el cálculo de este factor, aplicamos la siguiente ecuación:
P S
i
n
=
+
( )








1
1
(2)
Ejemplo
Factor simple de actualización (FSA)
Sebastián cuenta con un stock final de capital de $14.693,28, producto de un ahorro en el
Banco de Crédito quien paga una TNA de 8% durante 5 años a plazo fijo ¿Cuál fue su stock
inicial de capital, o cuánto tuvo que depositar hace 5 años para tener hoy $14.693,28?
Solución:
Los datos son:
P = ?
S = $14.693,28
i = 8%
n = 5 años
P = $10.000
S = $14.693,28
Final de año
0 1 2 3 4 5

160. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
160
La línea de tiempo para la operación es como sigue:
Sustituyendo los valores numéricos en la ecuación (2):
P =
+
( )








=
14 693 28
1
1 0 08
10 000
5
. ,
,
$ .
El stock inicial o valor actual fue de $10.000. Es decir, Sebastián tuvo que depositar hace
cinco años $10.000 para tener después de dicho plazo $14.693,28. 
4. FACTOR DE CAPITALIZACIÓN DE LA SERIE (FCS)
Conocido como factor de capitalización de una serie uniforme. Es el valor actual que se recibe o
paga en forma anual durante un período dado. Este factor traslada una serie uniforme compuesta
de rentas uniformes R o iguales hacia el momento final de la última renta S, aplicando una tasa
efectiva i cuyo plazo coincide con el plazo de cada una renta durante el número de períodos
capitalizados n contenidos en el horizonte temporal. La sigla original proviene del inglés “Uniform-
Series Compound-Amount Factor”, que en español significa “Factor Cantidad Compuesta Serie
Uniforme”.
Para el cálculo de este factor, se aplica la ecuación siguiente:
S R
i
i
n
=
+
( ) −








1 1
(3)
Ejemplo
Factor de capitalización de la serie (FCS)
Supongamos que Sebastián cuenta con una renta equivalente a $2.504,56 cada año,
disponible para ahorrarlo en el Banco de Crédito que paga 8% de interés anual, durante
cinco años. ¿Cuál es el stock final o valor futuro de dicha serie uniforme de capital?
Solución:
Los datos son:
S = ?
R = $2.504,56
P = $10.000
S = $14.693,28
Final de año
0 1 2 3 4 5

161. Cálculo financiero
P R O E S A D
161
i = 8%
n = 5 años
La línea de tiempo para la operación se muestra a continuación:
Reemplazando en la ecuación (3), tenemos:
S =
+
( ) −








=
2 504 56
1 0 08 1
0 08
14 693 28
5
. ,
,
,
$ . ,
El valor futuro asciende a $14.693,28, producto de la capitalización de seis rentas uniformes
de $2.504,56. 
5. FACTOR DE DEPÓSITO AL FONDO DE AMORTIZACIÓN (FDFA)
Conocido como factor de fondo de amortización. Es el monto de dinero que se destina para
un depósito uniforme anual, que es necesario cumplir anualmente. Este factor convierte una
cantidad ubicada en el futuro, S en una serie compuesta de renta uniformes equivalentes R,
aplicando una tasa efectiva i cuyo plazo coincide con el plazo de cada renta durante el número
de períodos capitalizados n contenidos en el horizonte temporal. Siendo éste un proceso inverso
del FSC. La sigla en inglés significa “Sinking Fund Deposit Factor”, siendo denominado por otros
tratadistas como “Factor Fondo de Amortización”
Para esto aplicamos la ecuación siguiente:
R S
i
i
n
=
+
( ) −








1 1
(4)
Ejemplo
Factor de depósito al fondo de amortización (FDFA)
Sebastián cuenta con un stock final de capital de $14.693,28, producto de sus ahorros en el
Banco de Crédito, que pagó una TNA de 8%, durante cinco años. ¿Cuál es el flujo constante
o renta anual que tuvo que depositar Sebastián para obtener un stock final de $14.693,28?
Capitalización
2.504,56 2.504,56 2.504,56 2.504,56 2.504,56
R R
$
R R R
0 1 2 3 4 5
3.407,43
3.155,03
2.921,32
2.704,93
2.504,55
$14.693,28

162. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
162
Solución:
Los datos son:
R = ?
S = $14.693,28
i = 8%
n = 5 años
El diagrama de tiempo para el FDFA es el siguiente:
Reemplazando en la ecuación (4), se obtiene:
R =
+
( ) −








=
14 693 28
0 08
1 0 08 1
2 504 56
5
. ,
,
,
$ . ,
Sebastián tuvo que depositar anualmente y por cinco años la suma de $2.504,56. 
6. FACTOR DE ACTUALIZACIÓN DE LA SERIE (FAS)
Conocido como factor de la serie uniforme cantidad compuesta. Es aquel monto de efectivo que
aumenta con los depósitos uniformes a fin de cada año, cuyo crecimiento se registra a interés
compuesto anualmente. Este factor trae al momento cero P una anualidad simple compuesta por
rentas uniformes R, aplicando una tasa efectiva i cuyo plazo coincide con el plazo de cada renta
durante el número de períodos capitalizados n contenidos en el horizonte temporal. Como tal es
una operación inversa al factor de recuperación del capital (FRC), siendo conocido en inglés como
“Uniform-Series Present-Worth Factor” y denominado por Tarquin como “factor Valor Presente
Serie Uniforme”.
Este factor es hallado aplicando la ecuación siguiente:
P R
i
i i
n
n
=
+
( ) −
+
( )








1 1
1
(5)
Descuento
2.504,56 2.504,56 2.504,56 2.504,56 2.504,56
R R R R R
0 1 2 3 4 5
S = $14.693,28

163. Cálculo financiero
P R O E S A D
163
Ejemplo
Factor de actualización de la serie (FAS)
Sebastián cuenta con una renta equivalente a $2.504,56 anuales, disponible para ahorrarlo
en el Banco de Crédito que paga una TNA de 8%, durante cinco años. ¿Cuál es el valor
actual de esa serie uniforme?
Solución:
Los datos son:
P = ?
R = $2.504,56
i = 8%
n = 5 años
El diagrama de tiempo para el FAS es el siguiente:
Sustituyendo los datos en la ecuación (5), se obtiene:
P =
+
( ) −
+
( )








=
2 504 56
1 0 08 1
0 08 1 0 08
10 000
5
5
. ,
,
, ,
$ .
El stock inicial o valor actual asciende a $10.000. 
7. FACTOR DE RECUPERACIÓN DEL CAPITAL (FRC)
Es el pago anual que se programa para cancelar el préstamo en el período establecido con interés
compuesto sobre el saldo no reembolsado. Este factor convierte una cantidad del presente P, en
una serie compuesta de rentas uniformes equivalentes R, aplicando una tasa efectiva i cuyo plazo
coincide con el plazo de cada renta durante el número de períodos capitalizados n contenidos
en el horizonte temporal. Este proceso es inverso al factor de actualización de la serie (FAS),
como tal, transforma un stock inicial de efectivo en un flujo constante. La sigla en inglés significa
“Capital Recovery Factor”.
Descuento
2.504,56 2.504,56 2.504,56 2.504,56 2.504,56
R R
$
R R R
0 1 2 3 4 5
2.319,04
2.147,26
1.988,20
1.840,93
1,704,57
$10.000.00

164. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad III
164
Este factor se halla aplicando la siguiente ecuación:
R P
i i
i
n
n
=
+
( )
+
( ) −








1
1 1
(6)
Ejemplo
Factor de recuperación del capital (FRC)
Sebastián cuenta con un capital inicial de $10.000, y desea colocarlo en el Banco de Crédito,
que paga una TNA de 8%, durante cinco años. ¿Cuál es el flujo constante o renta anual del
capital con que podrá contar los próximos cinco años?
Solución:
Los datos son:
R = ?
P = $10.000
i = 8%
n = 5 años
El diagrama de tiempo para el FRC es el siguiente:
Sustituyendo los valores en la ecuación (6), se obtiene:
R =
+
( )
+
( ) −








=
10 000
0 08 1 0 08
1 0 08 1
2 504 56
5
5
.
, ,
,
$ . ,
La cuota o flujo constante asciende a $2.504,56. 
2.504,56 2.504,56 2.504,56 2.504,56 2.504,56
R R R R R
0 1 2 3 4 5
P = $10.000

165. 165
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Factor simple de capitalización (FSC)
1. Carito deposita $2.500 en una cuenta de ahorros del BBVA que paga una TNA de 10,25%
capitalizable mensualmente. ¿Cuál es su stock final o valor futuro de capital después de dos
años? Rpta. $3.066,14
2. Kamila deposita $7.500 en una cuenta a plazo fijo del Interbank que paga una TNA de
12,75% capitalizable diariamente. ¿Cuál es su stock final o valor futuro de capital después de
18 meses? Rpta. $9.080,41
Factor simple de actualización (FSA)
3. Carito cuenta con un stock final de capital de $3.066,14, producto de un ahorro en el BBVA
a una TNA de 10,25% capitalizable mensualmente durante dos años. ¿Cuál fue su stock
inicial de capital, o cuánto tuvo que depositar hace dos años para tener hoy $3.066,14? Rpta.
$2.500

166. 166
4. Kamila cuenta con un stock final de capital de $9.080,41, producto de un ahorro a plazo fijo
en el Interbank una TNA de 12,75% capitalizable diariamente durante 18 meses. ¿Cuál fue su
stock inicial de capital, o cuánto tuvo que depositar hace 18 meses para tener hoy $9.080,41?
Rpta. $7.500
Factor capitalización de la serie (FCS)
5. Carito cuenta con una renta equivalente a $115,65 cada mes, disponible para ahorrarla en el
BBVA que paga una TNA de 10,25% capitalizable mensualmente, durante dos años. ¿Cuál es
el stock final o valor futuro del capital? Rpta. $3.066,14
6. Kamila cuenta con una renta equivalente a $15,26 cada día, disponible para ahorrarla en el
Interbank que paga una TNA de 12,75% capitalizable diariamente, durante 18 meses. ¿Cuál
es el stock final o valor futuro del capital? Rpta. $9.080,41
Factor de depósito al fondo de amortización (FDFA)
7. Carito cuenta con un stock final de capital de $3.066,14, producto de sus ahorros en el BBVA,
que pagó una TNA de 10,25% capitalizable mensualmente, durante dos años. ¿Cuál es el
flujo constante o renta mensual que tuvo que depositar Carito para obtener un stock final de
$3.066,14? Rpta. $115,65
8. Kamila cuenta con un stock final de capital de $9.080,41, producto de sus ahorros a plazo fijo
en el Interbank, que pagó una TNA de 12,75% capitalizable diariamente, durante 18 meses.
¿Cuál es el flujo constante o renta diaria que tuvo que depositar Kamila para obtener un stock
final de $9.080,41? Rpta. $15,261777

167. 167
Factor de actualización de la serie (FAS)
9. Carito cuenta con una renta equivalente a $115,65 mensuales, disponible para ahorrarla en
el BBVA que paga una TNA de 10,25% capitalizable mensualmente, durante dos años. ¿Cuál
es el stock inicial o valor actual de esa serie uniforme de capital? Rpta. $2.500
10. Kamila cuenta con una renta equivalente a $15,261777 diarios, disponible para ahorrarla
en el Interbank que paga una TNA de 12,75% capitalizable diariamente, durante 18 meses.
¿Cuál es el stock inicial o valor actual de esa serie uniforme de capital? Rpta. $7.500
Factor de recuperación del capital (FRC)
11. Carito cuenta con un capital inicial de $2.500 y desea colocarlo en el BBVA, que paga una TNA
de 10,25% capitalizable mensualmente, durante dos años. ¿Cuál es el flujo constante o renta
mensual del capital? Rpta. $115,65
12. Kamila cuenta con un capital inicial de $7.500 y desea colocarlo en el Interbank, que paga
una TNA de 12,75% capitalizable diariamente, durante 18 meses. ¿Cuál es el flujo constante
o renta diaria del capital? Rpta. $15,261777

169. ANUALIDADES Y PROGRAMAS DE AMORTIZACIÓN DE
CRÉDITOS
Sesión Nº 8: Anualidades vencidas y anticipadas
Sesión Nº 9: Anualidades diferidas y perpetuas
Sesión Nº 10: Programas de amortización de créditos
UNIDAD
IV
UNIDAD IV

170. COMPETENCIAS
CONCEPTUAL PROCEDIMENTAL ACTITUDINAL
Comprende las anuali-
dades y programas de
amortización de crédi-
tos.
Analizan y construyen
organizadores visuales
que permiten desarro-
llar ejercicios prácticos.
Interioriza los conteni-
dos desarrollados para
aplicarlos en su vida
profesional.

171. Cálculo financiero
P R O E S A D
171
8
Sesión
Anualidades y
programas de
amortización de
crÉdito
1. INTRODUCCIÓN
Una anualidad se define como una serie de pagos, por lo general iguales, realizados en intervalos
de tiempo. A simple vista el término anualidad parece implicar que los pagos se efectúan cada
año (anual); sin embargo, esto no es necesariamente así, ya que los pagos pueden ser mensuales,
quincenales, etc. Como ejemplos de anualidad tenemos:
• El cobro quincenal del sueldo.
• El pago mensual de la renta de la casa.
• Los pagos mensuales de la tarjeta de crédito.
• El pago mensual por el servicio del cable.
• Los abonos mensuales para pagar la computadora comprada al crédito.
• El pago de la prima del seguro de vida, etc.
Según Héctor Vidaurri Aguirre6
, “el concepto de anualidad es de gran importancia en matemática
financiera, ya que es muy frecuente que las transacciones comerciales impliquen una serie de
pagos hechos a intervalos iguales de tiempo, en vez de un pago único realizado al final del
plazo”.
El término transcurrido entre dos pagos sucesivos se llama período de pago o período de renta.
Este período de pago, tal como se ha mencionado, puede ser anual, semestral, mensual, etc.
Al tiempo que transcurre entre le primer periodo de pago y el final del último periodo de pago
se llama plazo de la anualidad.
Existen diversas formas de clasificar las anualidades, entre ellas tenemos:
a) Utilizando el tiempo
Entre ellas pueden ser ciertas y contingentes: Una anualidad cierta es aquella en la cual los
pagos comienzan y terminan en fechas perfectamente definidas. Por ejemplo, al comprar
un equipo de sonido en Saga Falabella, se establecen de antemano las fechas de iniciación
y terminación del crédito. Asimismo, una variante de este tipo de anualidades son las
anualidades perpetuas o perpetuidades. Estas anualidades se inician en una fecha fija y la
duración de los pagos es por tiempo limitado.
6
Profesor del Instituto Tecnológico de Estudios Superiores de Occidente (ITESO-México).

172. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
172
Una anualidad contingente es aquella en la cual la fecha del primer pago, la fecha del último
pago, o ambas dependen de algún suceso que se sabe que ocurrirá, pero no se sabe cuando.
Por ejemplo, el contrato de un seguro de vida en el Pacífico Perú Vida, donde se establece
que la suma asegurada se entregue al beneficiario del seguro en 6 o más pagos mensuales
iguales. Se sabe que los pagos deben efectuarse al morir el asegurado, pero ¿cuándo ocurrirá
esto?. Este tipo de anualidades no se estudiarán en este texto.
b) Utilizando los pagos
Dentro de éstas, pueden ser vencidas y anticipadas: Una anualidad vencida, también
llamada anualidad ordinaria, es aquella cuyos pagos se realizan al final de cada periodo de
pago.
Una anualidad anticipada es aquella cuyos pagos se realizan al principio de cada periodo de
pago.
c) Utilizando los intereses
Pueden ser simples o generales: Una anualidad simple, es aquella cuyo período de pago
coincide con el período de capitalización de los intereses. Por ejemplo, realizar depósitos
mensuales en una cuenta de ahorros que paga intereses capitalizables cada mes.
Una anualidad general es aquella cuyo período de pago no coincide con el período de
capitalización de los intereses. Por ejemplo, cuando se realizan depósitos quincenales en
una cuenta de ahorros cuyos intereses se capitalizan cada mes.
d) Utilizando el momento de iniciación de la anualidad
Dentro de esta clasificación tenemos, diferidas o inmediatas: Una anualidad diferida es
aquella en la cual los pagos se aplazan por un cierto tiempo. Por ejemplo, se compra hoy,
a crédito una computadora portátil, la cual se pagará mediante 12 pagos mensuales y el
primer pago se llevará a cabo después de 3 meses.
Una anualidad inmediata es aquella en la que no existe aplazamiento alguno de los pagos,
es decir, los pagos se realizan en el período inmediato a la firma del contrato o del pagaré.
De esto, tomando una característica de cada una de las diferentes clasificaciones, es posible
formar 16 tipos diferentes de anualidades. Por ejemplo:
• Anualidades ciertas, simples, vencidas e inmediatas.
• Anualidades contingentes, generales, vencidas y diferidas.
• Anualidades ciertas, simples, anticipadas y diferidas.
• Anualidades ciertas, simples, vencidas e inmediatas, etc.
Sin embargo, de estos 16 tipos de anualidades, las más usuales son:
• Las anualidades ciertas, simples, vencidas e inmediatas; conocidas simplemente como
anualidades vencidas.
• Las anualidades ciertas, simples, anticipadas e inmediatas; conocidas simplemente como
anualidades anticipadas.
• Las anualidades ciertas, simples, vencidas y deferidas; conocidas simplemente como
anualidades diferidas.

173. Cálculo financiero
P R O E S A D
173
En este capítulo nos ocuparemos de las primeras dos clases. A continuación, estudiaremos la
primera de ellas.
2. ANUALIDADES VENCIDAS U ORDINARIAS
De todas las clases o tipos de anualidades antes mencionadas, las anualidades vencidas u
ordinarias son las que se utilizan con mayor frecuencia en el mundo financiero. Su característica
principal recae en que los pagos se realizan al final de cada periodo de pago.
2.1. Valor futuro S de una anualidad vencida
El monto o valor futuro de una anualidad vencida es el valor acumulado de una serie de pagos
iguales efectuados al final de cada periodo de pago.
Para el cálculo del valor futuro de una anualidad vencida, se utiliza el factor de capitalización de
la serie (FCS), cuya ecuación es la siguiente:
S R
i
i
n
=
+
( ) −








1 1
(1)
Ejemplo 1
Valor futuro S de una anualidad vencida
Supóngase que se deposita $1.000 al final de cada mes en un banco que paga una TEM de
1,5% capitalizable cada mes. ¿Cuál será el monto al finalizar el cuarto mes?
Solución:
Los datos son:
S = ?
R = $1.000
i = 1.5%
n = 4 meses
El diagrama de tiempo es el siguiente:
Nótese que el cero en el diagrama de tiempo corresponde al momento actual y coincide
con el inicio del mes 1; el número 1 marcado en el diagrama de tiempo corresponde al
final del mes 1 y coincide con el inicio del mes 2, y así sucesivamente.
$1.000
0 1 2 3 4
S
meses
$1.000 $1.000 $1.000

174. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
174
Debido a que los depósitos se realizan al final de cada mes, los primeros $1.000 ganarán
intereses por 3 meses, los segundos $1.000 ganarán intereses por 2 meses, etc. El último
depósito no gana intereses.
Ahora, si la fecha focal se localiza en el momento final, o al final de la cuarta renta,
entonces se puede formar la siguiente ecuación de valor:
S = ( ) + ( ) + ( ) +
1 000 1 015 1 000 1 015 1 000 1 015 1 000
3 2 1
. * , . * , . * , .
S = $ . ,
4 090 90
Reemplazando en la ecuación (1), hallamos el mismo resultado:
S =
+
( ) −








=
1 000
1 0 015 1
0 015
4 090 90
4
.
,
,
$ . ,
El valor futuro de la anualidad asciende a $4.090,90, producto de la capitalización de
cuatro rentas iguales de $1.000. 
Ejemplo 2
Valor futuro S de una anualidad vencida
El papá de un niño de 10 años empieza a ahorrar para que su hijo pueda estudiar una
carrera universitaria. Para esto planea depositar $200 en una cuenta de ahorros al final de
cada mes y durante los próximos 8 años. Si la TNA es del 27% capitalizable mensualmente.
¿Cuál será el monto de la cuenta al cabo de 8 años?
Solución:
Los datos son:
S = ?
R = $200
i = 27%
n = 8 años
Reemplazando los valores en la ecuación (1), tenemos:
S =
+





 −




















=
( )( )
200
1
0 27
12
1
0 27
12
66
8 12
,
,
$ .
. ,
364 47
El valor futuro de la anualidad asciende a $66.364,47. Al final de los 8 años la cuenta
asciende a $66.364,47. 

175. Cálculo financiero
P R O E S A D
175
Renta uniforme en función de S
Despejando R en la ecuación (1), encontramos la fórmula que nos permite calcular el valor de
las rentas uniformes, en función del valor futuro o monto. Esta fórmula es el factor de depósito
al fondo de amortización (FDFA):
R S
i
i
n
=
+
( ) −








1 1
(2)
Ejemplo 3
Renta uniforme en función de S
A cuánto ascenderá el depósito al final de cada mes que un padre de un niño de 10 años
tendrá que hacer, para que su hijo pueda estudiar una carrera universitaria y poder juntar
un monto de $66.364,47, si se considera una TNA del 27% capitalizable mensualmente y
si estos depósitos se van hacer durante 8 años.
Solución:
Los datos son:
R = ?
S = $66.364,47
i = 27%
n = 8 años
Sustituyendo los valores en la (2), tenemos:
R =






+





 −












( )( )
66 364 47
0 27
12
1
0 27
12
1
8 12
. ,
,
,



= $200
El padre de familia tendrá que depositar al final de cada mes $200, durante 8 años para
que al final de los mismos pueda tener $66.364,47. 
Cálculo de n en función de S
Despejando n en la ecuación (1), se encuentra la fórmula que nos permite calcular el número de
las rentas uniformes, en función del valor futuro o monto.
n
s i
R
i
=
+






+
( )
log
*
log
1
1
(3)

176. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
176
Ejemplo 4
Cálculo de n en función de S
En cuanto tiempo, un padre de familia obtendrá un monto de $66.364,47, si efectúa
depósitos mensuales al final de los mismos de $200, a una TNA de 27% capitalizable
mensualmente.
Solución:
Los datos son:
n = ?
S = $66.364,47
R = $200
i = 27%
Sustituyendo los valores en la (3), tenemos:
n =
+


















+



log
. , *
,
log
,
1
66 364 47
0 27
12
200
1
0 27
12




= 96
El padre de familia tendrá que efectuar 96 depósitos al final de cada mes de $200 para que
al final de los mismos pueda tener $66.364,47. 
2.2. Valor presente P de una anualidad vencida
Hasta aquí hemos determinado el valor futuro (S) de una anualidad. A continuación vamos a
determinar el valor presente o valor actual (P) de una anualidad vencida; esto es el valor al
comienzo del plazo. El valor presente de una anualidad se define como la suma de los valores
presentes de todos los pagos.
Para el cálculo del valor actual de una anualidad vencida, se utiliza el factor de actualización de
la serie (FAS), cuya ecuación es la siguiente:
P R
i
i i
n
n
=
+
( ) −
+
( )








1 1
1
(4)
Ejemplo 1
Valor presente P de una anualidad vencida
Supóngase que una persona va a liquidar una deuda mediante 4 pagos al final de cada

177. Cálculo financiero
P R O E S A D
177
mes de $1.000 cada uno, que incluyen intereses a una TEM de 2% con capitalización cada
mes. Se desea obtener el valor presente de los pagos.
Solución:
Los datos son:
P = ?
R = $1.000
i = 2%
n = 4 meses
El diagrama de tiempo es el siguiente:
Ahora, si la fecha focal se localiza en el momento actual, entonces se puede formar la
siguiente ecuación de valor:
P =
( )
+
( )
+
( )
+
( )
=
1 000
1 02
1 000
1 02
1 000
1 02
1 000
1 02
3 8
1 2 3 4
.
,
.
,
.
,
.
,
$ . 0
07 73
,
Del mismo modo, reemplazando en la ecuación (4), tenemos:
P =
+
( ) −
+
( )








=
1 000
1 0 02 1
0 02 1 0 02
3 807 73
4
4
.
,
, ,
$ . ,
De esto, podemos señalar que $3.807,73 es el valor actual de 4 pagos al final de cada mes
de $1.000 cada uno, y representa la cantidad de dinero pedida en préstamo por el deudor.
El valor presente de una anualidad se puede interpretar, también, como la cantidad que se
debe invertir en este momento para poder efectuar cierto número de retiros en el futuro.
Esto es, si una persona invierte en este momento $3.807,73 al 2% mensual capitalizable
cada mes, entonces podrá retirar $1.000 cada mes, durante 4 meses. 
Ejemplo 2
Valor presente P de una anualidad vencida
La señora Norma Morales está apunto de jubilarse y estima que necesitará $2.000 cada
$1.000 $1.000 $1.000 $1.000
0 1 2 3 4
P
meses

178. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
178
mes durante los próximos 15 años. Su banco le paga una TNA de 20% capitalizable
mensualmente. ¿Cuánto dinero debe tener depositado para poder retirar la cantidad
especificada cada mes?
Solución:
Los datos son:
P = ?
R = $2.000
i = 20%
n = 15 años
Sustituyendo los valores en la ecuación (4), se tiene:
P =
+





 −
+






( )( )
( )(
2 000
1
0 20
12
1
0 20
12
1
0 20
12
15 12
15 12
.
,
, ,
)
)














= $ . ,
113 875 99
La señora Norma Morales debe tener un depósito en el banco de $113.875,99. 
Renta uniforme en función de P
Despejando R en la ecuación (1), encontramos la fórmula que nos permite calcular el valor de
las Despejando R en la ecuación (4), encontramos la fórmula que nos permite calcular el valor
de las rentas uniformes, en función del valor presente o valor actual. Esta fórmula es el factor de
recuperación del capital (FRC):
R P
i i
i
n
n
=
+
( )
+
( ) −








1
1 1
(5)
Ejemplo 3
Renta uniforme en función de P
La señora Norma Morales está a punto de jubilarse y cuenta con unos ahorros en el banco,
los cuales ascienden a $113.875,99 que gana una TNA de 20% capitalizable mensualmente.
¿Cuál es el flujo constante o renta mensual del capital con que podrá contar la señora
Norma para los próximos 15 años?
Solución:
Los datos son:
R = ?
P = $113.875,99
i = 20%
n = 15 años

179. Cálculo financiero
P R O E S A D
179
Reemplazando los valores en la ecuación (5), se tiene:
R =
+






+






( )( )
( )
113 875 99
0 20
12
1
0 20
12
1
0 20
12
15 12
15
. ,
, ,
,
1
12
1
2 000
( )
−














= $ .
La señora Norma Morales podrá contar mensualmente y por un espacio de 15 años, la
suma de $2.000 mensuales. 
Cálculo de n en función de P
Despejando n en la ecuación (4), se encuentra la fórmula que nos permite calcular el número de
las rentas uniformes, en función del valor presente o valor actual.
n
P i
R
i
=
− −






+
( )
log
*
log
1
1
(6)
Ejemplo 4
Cálculo de n en función de P
La señora Norma Morales está apunto de jubilarse cuenta con unos ahorros en el banco, los
cuales ascienden a $113.875,99 que gana una TNA de 20% capitalizable mensualmente.
Asimismo, estima que necesitará $2.000 mensuales para gastos diversos. ¿Por cuántos
meses podrá contar la señora Norma con dicha cantidad de dinero?
Solución:
Los datos son:
n = ?
P = $113.875,99
R = $2.000
i = 20%
Reemplazando los valores en la ecuación (6), se tiene:
n =
− −


















+
log
. . *
,
.
log
,
1
113 875 99
0 20
12
2 000
1
0 20
12
2
180






=
La señora Norma Morales podrá contar con $2.000 mensuales durante 180 meses. 

180. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
180
3. ANUALIDADES ANTICIPADAS
Una anualidad anticipada es aquella en la cual los pagos se llevan a cabo al inicio del período
de pago, a diferencia de una anualidad vencida, en que los pagos se llevan a cabo al final. Como
ejemplos tenemos: los pagos anuales (primas) de seguro de vida, la renta de una casa u oficina,
etc.
La diferencia cuantitativa entre una anualidad vencida y una anualidad anticipada (Ver figura 1)
radica en que en la primera, la última renta no percibe intereses pues coincide con el final del
cobro; mientras que en la segunda la última renta se abona o cobra al empezar el último período,
de tal forma que percibe intereses en este último periodo.
Se puede observar que la anualidad anticipada comienza con un pago y concluye un período
después de que se haya cubierto el último pago. De esta manera, el n-ésimo pago gana intereses
por un periodo debido a que fue depositado al inicio del último periodo.
3.1. Valor futuro S de una anualidad anticipada
El monto o valor futuro de una anualidad anticipada es el valor acumulado de una serie de pagos
iguales efectuados al inicio de cada periodo de pago.
Para el cálculo del valor futuro de una anualidad anticipada, se utiliza la ecuación siguiente:
S R
i i
i
n
=
+
( ) − +
( )








+
*
1 1
1
(7)
Figura 1
Anualidades vencidas y anticipadas
Anualidad Vencida
R R R R
0 1 2 3 n-3 n-2 n-1 n
R R R
Anualidad Anticipada
R
R R R R
0 1 2 3 n-3 n-2 n-1 n
R R R

181. Cálculo financiero
P R O E S A D
181
Ejemplo 1
Valor futuro S de una anualidad anticipada
Supóngase que se deposita $1.000 al inicio de cada mes en un banco que paga una TEM
de 1,5% capitalizable cada mes. ¿Cuál será el monto al finalizar el cuarto mes?
Solución:
Los datos son:
S = ?
R = $1.000
i = 1.5%
n = 1 año
El diagrama de tiempo es el siguiente:
Nótese que el cero en el diagrama de tiempo corresponde al momento actual y coincide
con el inicio del mes 1; el número 1 marcado en el diagrama de tiempo corresponde al
final del mes 1 y coincide con el inicio del mes 2, y así sucesivamente.
Debido a que los depósitos se realizan al inicio de cada mes, los primeros $1.000 ganarán
intereses por 4 meses, los segundos $1.000 ganarán intereses por 3 meses, etc. El último
depósito gana intereses por un mes.
Ahora, si la fecha focal se localiza en el momento final, o al final de la cuarta renta,
entonces se puede formar la siguiente ecuación de valor:
S = ( ) + ( ) + ( ) +
1 000 1 015 1 000 1 015 1 000 1 015 1 000 1 015
4 3 2
. * , . * , . * , . * ,
(
( )
1
S = $ . ,
4 152 26
Reemplazando en la ecuación (7), hallamos el mismo resultado:
S =
+
( ) − +
( )








=
+
1 000
1 0 015 1 0 015
0 015
4 152 26
4 1
. *
, ,
,
$ . ,
El valor futuro de la anualidad asciende a $4.152,26, producto de la capitalización de
cuatro rentas iguales de $1.000. 
$1.000 $1.000 $1.000 $1.000
0 1 2 3 4
S
meses

182. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
182
Ejemplo 2
Valor futuro S de una anualidad anticipada
El papá de un niño de 10 años empieza a ahorrar para que su hijo pueda estudiar una
carrera universitaria. Para esto planea depositar $200 en una cuenta de ahorros al inicio de
cada mes y durante los próximos 8 años. Si la TNA es del 27% capitalizable mensualmente.
¿Cuál será el monto de la cuenta al cabo de 8 años?
Solución:
Los datos son:
S = ?
R = $200
i = 27%
n = 8 años
Sustituyendo los valores en la (7), tenemos:
S =
+





 − +










( )( )

 
+
200
1
0 27
12
1
0 27
12
0 27
12
8 12 1
*
, ,
,











= $ . ,
67 857 67
El valor futuro de la anualidad asciende a $67.857,67. Al final del de los 8 años la cuenta
asciende a $67.857,67. 
Renta uniforme en función de P
Despejando R en la ecuación (7), encontramos la fórmula que nos permite calcular el valor de
las rentas uniformes, en función del valor futuro o monto.
R
S i
i i
n
=
+
( ) − +
( )




+
*
1 1
1 (8)
Ejemplo 3
Renta uniforme en función de P
A cuanto ascenderá el depósito al inicio de cada mes que un padre de un niño de 10 años
tendrá que hacer, para que su hijo pueda estudiar una carrera universitaria y poder juntar
un monto de $67.857,67, si se considera una TNA del 27% capitalizable mensualmente y
si estos depósitos se van hacer durante 8 años.
Solución:

183. Cálculo financiero
P R O E S A D
183
Los datos son:
R = ?
S = $67.857,67
i = 27%
n = 8 años
Sustituyendo los valores en la (8), tenemos:
R =






+





 − +
( )( )

 
+
67 857 67
0 27
12
1
0 27
12
1
0 27
8 12 1
. . *
,
, ,
1
12
200














= $
El padre de familia tendrá que depositar al inicio de cada mes $200, durante 8 años para
que al final de los mismos pueda tener $67.857,67. 
Cálculo de n en función de S
Despejando n en la ecuación (7), se encuentra la fórmula que nos permite calcular el número de
las rentas uniformes, en función del valor futuro o monto.
n
S i
R
i
i
=
+ +






+
( )
−
log
*
log
1
1
1 (9)
Ejemplo 4
Cálculo de n en función de S
En cuanto tiempo, un padre de familia obtendrá un monto de $67.857,67, si efectúa
depósitos mensuales al inicio de los mismos de $200, a una TNA de 27% capitalizable
mensualmente.
Solución:
Los datos son:
n = ?
S = $67.857,67
R = $200
i = 27%
Sustituyendo los valores en la (9), tenemos:

184. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
184
n =






+ +


















log
. , *
,
,
l
67 857 67
0 27
12
200
1
0 27
12
o
og
,
1
0 27
12
1 97
+






− =
El padre de familia tendrá que efectuar 97 depósitos al inicio de cada mes de $200 para
que al final de los mismos pueda tener $67.857,67. 
3.2. Valor presente P de una anualidad anticipada
Hasta aquí hemos determinado el valor futuro (S) de una anualidad. A continuación vamos a
determinar el valor presente o valor actual (P) de una anualidad anticipada; esto es el valor al
comienzo del plazo. El valor presente de una anualidad se define como la suma de los valores
presentes de todos los pagos.
Para el cálculo del valor actual de una anualidad anticipada, se utiliza la siguiente ecuación:
P R
i i
i
n
=
+
( ) − +
( )








−
*
1 1
1
(10)
Ejemplo 1
Valor presente P de una anualidad anticipada
Supóngase que una persona va a liquidar una deuda mediante 4 pagos al inicio de cada
mes de $1.000 cada uno, que incluyen intereses a una TEM de 2% con capitalización cada
mes. Se desea obtener el valor presente de los pagos.
Solución:
Los datos son:
P = ?
R = $1.000
i = 2%
n = 4 meses
El diagrama de tiempo es el siguiente:
$1.000 $1.000 $1.000 $1.000
0 1 2 3 4
P
meses

185. Cálculo financiero
P R O E S A D
185
Ahora, si la fecha focal se localiza en el momento actual, entonces se puede formar la
siguiente ecuación de valor:
P = +
( )
+
( )
+
( )
1 000
1 000
1 02
1 000
1 02
1 000
1 02
1 2 3
.
.
,
.
,
.
,
P = $ . ,
3 883 88
Del mismo modo, reemplazando en la ecuación (10), tenemos:
P =
+
( ) − +
( )








=
−
1 000
1 0 02 1 0 02
0 02
3 883 88
1 4
. *
, ,
,
$ . ,
De esto, podemos señalar que $3.883,88 es el valor actual de 4 pagos al inicio de cada
mes de $1.000 cada uno, y representa la cantidad de dinero pedida en préstamo por el
deudor. 
Ejemplo 2
Valor presente P de una anualidad anticipada
La señora Norma Morales está apunto de jubilarse y estima que necesitará $2.000 al
inicio de cada mes durante los próximos 15 años. Su banco le paga una TNA de 20%
capitalizable mensualmente. ¿Cuánto dinero debe tener depositado para poder retirar la
cantidad especificada cada mes?
Solución:
Los datos son:
P = ?
R = $2.000
i = 20%
n = 15 años
Reemplazando los valores en la ecuación (10), se tiene:
P =
+





 − +







− ( )( )

 

2 000
1
0 20
12
1
0 20
12
0 20
12
1 15 12
. *
, ,
,




















= $ . ,
115 773 93
La señora Norma Morales debe tener un depósito en el banco de $115.773,93. 

186. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
186
Renta uniforme en función de P
Despejando R en la ecuación (10), encontramos la fórmula que nos permite calcular el valor de
las rentas uniformes, en función del valor presente o valor actual.
R
P i
i i
n
=
+
( ) − +
( )




−
*
1 1
1 (11)
Ejemplo 3
Renta uniforme en función de P
La señora Norma Morales está a punto de jubilarse y cuenta con unos ahorros en el banco,
los cuales ascienden a $115.773,93 que gana una TNA de 20% capitalizable mensualmente.
¿Cuál es el flujo constante o renta mensual del capital con que podrá contar la señora
Norma para los próximos 15 años?
Solución:
Los datos son:
R = ?
P = $115.773,93
i = 20%
n = 15 años
Reemplazando los valores en la ecuación (11), se tiene:
R =






+





 − +






−
115 773 93
0 20
12
1
0 20
12
1
0 20
12
1 15
. , *
,
, ,
*
*
$ .
12
2 000
( )








=
La señora Norma Morales podrá contar mensualmente y por un espacio de 15 años, la
suma de $2.000 mensuales. 
Cálculo de n en función de P
Despejando n en la ecuación (10), se encuentra la fórmula que nos permite calcular el número
de las rentas uniformes, en función del valor presente o valor actual.
n
i
P i
R
i
= −
+ −






+
( )
1
1
1
log
*
log
(12)

187. Cálculo financiero
P R O E S A D
187
Ejemplo 4
Cálculo de n en función de P
La señora Norma Morales está a punto de jubilarse cuenta con unos ahorros en el banco, los
cuales ascienden a $115.773,93 que gana una TNA de 20% capitalizable mensualmente.
Asimismo, estima que necesitará $2.000 mensuales para gastos diversos. ¿Por cuántos
meses podrá contar la señora Norma con dicha cantidad de dinero?
Solución:
Los datos son:
n = ?
P = $115.773,93
R = $2.000
i = 20%
Reemplazando los valores en la ecuación (12), se tiene:
n = −
+





 −














1
1
0 20
12
115 773 93
0 20
12
2 000
log
,
. , *
,
.





+






=
log
,
1
0 20
12
180
La señora Norma Morales podrá contar con $2.000 mensuales durante 180 meses. 

188. 188
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Valor futuro S de una anualidad vencida
1. Una familia desea empezar a ahorrar para realizar un viaje a la ciudad de Acapulco. Para esto
se deposita cada fin de mes $200 en una cuenta bancaria que genera intereses a una TNA
del 16% capitalizable mensualmente. Se tiene planeado viajar en un año, ¿cuánto se habrá
ahorrado al final del año? Rpta. $2.584,06
2. En el momento de cumplir, su hija, su primer cumpleaños un señor depositó $1.500 en una
cuenta que abona una TNA de 8%; dicha cantidad la consigna cada cumpleaños. Al cumplir
12 años, aumentó sus consignaciones a $3.000. Calcular la suma que tendrá a disposición de
ella a los 18 años. Rpta. $51.736,64
3. Una persona deposita $100 al final de cada mes en una cuenta que abona una TNA de
6%, capitalizable mensualmente. Calcular su saldo en la cuenta, al cabo de 20 años. Rpta.
$46.204,09
4. A cuánto ascenderá el depósito al final de cada mes que una familia tendrá que efectuar en
un banco local para realizar un viaje a Acapulco y poder juntar un monto de $2.584,06, si se
considera una TNA del 16% capitalizable mensualmente y si estos depósitos se van hacer
durante 1 año. Rpta. $200

189. 189
5. En cuánto tiempo, una familia obtendrá un monto de $2.584,06, si efectúa depósitos
mensuales al final de los mismos de $200, a una TNA de 16% capitalizable mensualmente.
Rpta. 12 depósitos mensuales
Valor presente P de una anualidad vencida
6. Calcular el valor de contado de una propiedad vendida en las siguientes condiciones: $20.000
de contado; $1.000 por mensualidades vencidas durante 2 años y 6 meses y un último pago
de $2.500 un mes después de pagada la última mensualidad. Para el cálculo, utilizar una TNA
de 9% con capitalización mensual. Rpta. $48.758,17
7. ¿Cuál es el valor de contado de un equipo comprado con el siguiente plan: $14.000 de cuota
inicial; $1.600 mensuales durante 2 años 6 meses con un último pago de $2.500, al final del
último pago, si se carga una TNA de 12% con capitalización mensual? Rpta. $57.128,78
8. Una mina en explotación, ubicada en el centro del Perú, tiene una producción anual de
$8.000.000 y se estima que se agotará en 10 años. Hallar el valor presente de la producción,
si el rendimiento del dinero es de una TNA de 8%. Rpta. $53.680.651,19
9. Un distribuidor de automóviles ofreció al señor Jaime Cucho un automóvil Audi del año
mediante un pago inicial de $8.000 y 30 pagos mensuales de $2.866,66 cada uno. Si la
casa distribuidora aplica una TNA de 30% capitalizable mensualmente, encuentre el valor de
contado del automóvil. Rpta. $68.000
10. Un distribuidor de automóviles ofreció al señor Jaime Cucho un automóvil Audi del año al
precio de contado de $68.000. Asimismo, existe la posibilidad de financiarlo con un pago
inicial de $8.000 y 30 pagos mensuales. Si la casa distribuidora aplica una TNA de 30%
capitalizable mensualmente, encuentre el valor de cada cuota. Rpta. $2.866,66
Valor futuro S de una anualidad anticipada
11. ¿Cuál es el monto al cabo de 8 años si al inicio de cada bimestre se depositan $750 en una
cuenta de ahorros, si la TNA es de 7,35% capitalizable cada dos meses? Rpta. $49.205,51
12. Susy Gonzáles depositó $210 al principio de cada mes en un fondo que paga una TNA de
16% convertible mensualmente. Después de 2 años ella no hizo más depósitos, pero dejó el
dinero en depósito por otros dos años y medio a la misma tasa de interés. ¿A cuánto asciende
el fondo al final de ese tiempo? Rpta. $8.886,45
13. ¿Qué cantidad se debe depositar al inicio de cada bimestre durante 10 años para acumular
$100.000, si la TNA es del 7,44% capitalizable cada bimestre. Rpta. $1.118,83
14. ¿Cuántos depósitos mensuales anticipados de $1.000,80 cada uno deben hacerse, con el fin
de tener un monto de $100.000? La TEM es del 2,5%. Rpta. 50 depósitos mensuales
15. ¿Qué cantidad se debe depositar al inicio de cada mes para acumular $150.000 en dos y
medio años, si la TEM es del 1,57% capitalizable cada mes? Rpta. $3.891,93

190. 190
Valor presente P de una anualidad anticipada
16. Calcular el valor de Contado de una propiedad vendida a 15 años de plazo, con pagos de
$3.000 mensuales por mes anticipado, si la TNA es del 12% convertible mensualmente. Rpta.
$252.464,64
17. ¿Cuál es el valor presente de una renta de $500 depositada a principio de cada mes, durante
15 años en una cuenta de ahorros que gana una TNA de 9%, convertible mensualmente?
Rpta. $49.666,42
18. Una persona renta un departamento por $2.150 al mes durante un año. La renta se debe
pagar por adelantado cada mes. ¿Cuál es valor actual de las rentas de un año, tomando como
base una TNA de 21,5%. Rpta. $23.443,27
19. Una computadora puede ser adquirida pagando $170 de pago inicial y 24 pagos de $170
cada uno. ¿Cuál es el precio de contado si el interés cobrado es una TNA de 32% capitalizable
mensualmente? ¿Qué cantidad de interés se está pagando? Rpta. $3.155,21; $1.094,79
20. ¿Qué suma debe depositarse a principio de cada año, en un fondo que abona una TNA de
6% para proveer la sustitución de los equipos de una empresa cuyo costo es de $2.000.000
y con una vida útil de 5 años, si el valor de salvamento se estima en el 10% del costo? Rpta.
$301.239,17

191. Cálculo financiero
P R O E S A D
191
9
Sesión
Anualidades diferidas
y perpetuas
1. INTRODUCCIÓN
Cuando en un contrato de crédito u operación similar que debe amortizarse con cuotas uniformes,
por acuerdo expreso de las partes, el pago de esas rentas empieza después del vencimiento de
uno o varios períodos de renta, contados a partir del inicio del plazo pactado, se está ante el caso
de una anualidad diferida.
2. ANUALIDADES DIFERIDAS
Una anualidad diferida es aquella cuyo plazo comienza hasta después de transcurrido un cierto
intervalo de tiempo; desde el momento en que la operación quedó formalizada recibe el nombre
momento inicial o de convenio.
El intervalo de tiempo que transcurre entre el momento inicial y el inicio del plazo de la anualidad
se llama período de gracia o período de diferimiento. El período de gracia se mide utilizando
como unidad de tiempo el correspondiente a los períodos de pago. Por ejemplo, si dentro de
cuatro meses se dará el primer pago de una anualidad vencida de $500 mensuales, y cuyo plazo
es de seis meses, se tendrá el siguiente diagrama de tiempo.
En este ejemplo el período de gracia es de 3 años, ya que el final del tercer mes coincide con el
comienzo de la anualidad vencida, el cual es de 6 meses.
Para resolver problemas de anualidades diferidas no es necesario deducir nuevas fórmulas, ya
que éstas pueden ser tratadas como anualidades vencidas o anticipadas. En este libro, al resolver
Momento
Inicial
Período
de gracia
Comienzo del plazo
de la anualidad
Plazo de la anualidad
500 500 500 500 500 500
meses
0 1 2 3
0 1 2 3 4 5 6
4 5 6 7 8 9

192. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
192
problemas de anualidades diferidas, éstas se tratarán como anualidades vencidas, ya que esto
es lo más usual.
2.1. Valor futuro S de una anualidad diferida
El monto o valor futuro de una anualidad diferida es el valor acumulado de una serie de pagos
iguales efectuados después de transcurrido un cierto intervalo de tiempo, desde el momento en
que una determinada operación quedó formalizada.
Ejemplo 1
Valor futuro S de una anualidad diferida
La compañía Holandesa Foretrend Company adquiere unos yacimientos de mineral; los
estudios de ingeniería muestran que los trabajos preparatorios y vías de acceso demorarán
6 años. Se estima que los yacimientos en explotación rendirán una ganancia anual de
$2.400,000, suponiendo que la TNA es del 8% y que los yacimientos se agotarán después
de 15 años continuos de explotación, hállese el valor futuro de la renta que espera
obtenerse.
Solución:
Los datos son:
S = ?
R = $2.400.000
i = 8%
n = 15 años
El diagrama de tiempo es el como sigue:
En el diagrama R, representa la ganancia anual.
Para calcular el valor futuro de una serie uniforme de rentas, utilizamos la fórmula del FCS.
Reemplazando los valores en la ecuación del FCS, se tiene:
S =
+
( ) −








=
2 400 000
1 0 08 1
0 08
65 165 073 43
15
. .
,
,
$ . . ,
El valor futuro de las ganancias asciende a $65.165.073,43. 
R R R R R R
0 6 7 8 19 20 21 Años

193. Cálculo financiero
P R O E S A D
193
2.2. Valor presente P de una anualidad diferida
El valor presente de una anualidad diferida se define como la suma de los valores presentes de
una serie de pagos iguales efectuados después de transcurrido un cierto intervalo de tiempo
desde el momento en que una determinada operación quedó formalizada.
Ejemplo 1
Valor presente P de una anualidad diferida
En el problema anterior, hallar el valor presente de las utilidades que la compañía Holandesa
Foretrend Company obtendrá, al momento de adquirir los yacimientos de mineral.
Solución:
Los datos son:
P = ?
R = $2.400.000
i = 8%
n = 15 años
En el problema anterior, hallar el valor presente de las utilidades que la compañía Holandesa
Foretrend Company obtendrá, al momento de adquirir los yacimientos de mineral.
En éste, tal como observamos en el diagrama de tiempo anterior, las ganancias se producen
a partir del año 7 hasta el año 21, lo que tenemos que hacer primero es actualizar esa
serie uniforme de beneficios, hasta el inicio del año 7 o finales del año 6, que es lo mismo.
Para esto utilizamos el factor de actualización de la serie (FAS).
Reemplazando los valores en la ecuación del FAS, se tiene:
P =
+
( ) −
+
( )








=
2 400 000
1 0 08 1
0 08 1 0 08
20 542 748
15
15
. .
,
, ,
$ . . ,8
85
La serie uniforme R de beneficios actualizada al inicio del año 7, asciende a $20.542.748,85.
Una vez que tenemos esta cantidad, la misma la actualizamos hasta el momento 0, que es
la fecha en que la compañía adquiere los yacimientos de mineral. Para esto, actualizamos
dicho importe, utilizando el factor simple de actualización (FSA).
Reemplazando los valores en la ecuación del FSA, se tiene:
P =
+
( )








=
20 542 748 85
1
1 0 08
12 945 416 38
6
. . ,
,
$ . . ,
El valor presente de los beneficios que obtendrá Foretrend Company por la adquisición de
los yacimientos de mineral asciende a $12.945.416,38. 

194. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
194
Renta uniforme en función de P
Para calcular la renta uniforme en una anualidad diferida, se debe tener en cuenta que mientras
transcurre el período de gracia, una de las siguientes situaciones se lleva a cabo:
1. Que al final de cada período de pago se liquiden o paguen los intereses generados por el
capital original. Es este caso estamos hablando de un período de gracia normal o parcial.
2. Que los intereses generados dentro del período de gracia se capitalicen. En este caso, esta-
mos frente a un período de gracia total.
En la mayor parte de las situaciones reales se lleva a cabo la segunda opción, pero a continuación
veremos algunos ejemplos de cada uno de ellos.
Ejemplo 1
Renta uniforme en función de P
El señor Víctor Gómez obtiene un préstamo del Banco Intesa por $50.000, el mismo que
será destinado para la compra de un auto 0 km. BMW-Serie 5. El préstamo se pagará a
través de 60 pagos mensuales, después de un período de gracia total (los intereses no se
pagan, si no se capitalizan) de un año. Obtenga el valor del pago mensual sabiendo que
la TNA es del 27% capitalizable cada mes.
Solución:
Los datos son:
R = ?
P = $50.000
i = 27%
n = 5 años
El diagrama de tiempo es el como sigue:
Ahora, como los intereses no se pagan, sino se capitalizan, al final del período de gracia,
nuestra deuda ya no sigue siendo la misma ($50.000), a esto hay que sumarle los intereses.
Para esto, capitalizamos los intereses, utilizando el factor simple de capitalización (FSC),
como sigue:
S = +





 =
50 000 1
0 27
12
65 302 50
12
. *
,
$ . ,
50.000
0 1 2 11 12
0 1
R R R R R
2 58 59 60
13 14 70 71 72 meses
plazo de la
anualidad

195. Cálculo financiero
P R O E S A D
195
Una vez que conozco a cuánto asciende mi deuda, después de terminado el período
de gracia, recién puedo hallar el valor de cada cuota. Para esto utilizamos el factor de
recuperación del capital (FRC).
Reemplazando los valores en la ecuación del FRC, se tiene:
R =





 +






+





 −

65 302 50
0 27
12
1
0 27
12
1
0 27
12
1
60
60
. ,
, ,
,














= $ . ,
1 994 03
El valor de cada cuota, asciende a $1.994,03. El préstamo será cancelado con 60 cuotas
mensuales de $1.994,03. 
Ejemplo 2
Renta uniforme en función de P
Resuelva el problema anterior, suponiendo que el banco Intesa, sólo nos ofrece un período
de gracia normal, vale decir, durante el periodo de gracia se pagan los intereses.
Solución:
Los datos son:
R = ?
P = $50.000
i = 27%
n = 5 años
En este caso Víctor, tendrá que pagar los intereses mensuales que general el capital,
durante todo el periodo de gracia.
Ahora, una vez finalizado el período de gracia, nuestra deuda sigue siendo la misma
($50.000), esto porque durante el período de gracia se pagaron los intereses. A continuación,
hallamos el valor de cada cuota, utilizando el FRC:
R =





 +






+





 −




50 000
0 27
12
1
0 27
12
1
0 27
12
1
60
60
.
, ,
,











= $ . ,
1 526 77
El valor de cada cuota, asciende a $1.526,77. Asimismo, se puede observar que el interés total
pagado cuando los intereses se capitalizan (período de gracia total) durante todo el período de
gracia, es mayor que cuando los intereses se pagan (período de gracia parcial). 

196. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
196
3. PERPETUIDADES
Una renta perpetua o perpetuidad es una anualidad cuyo plazo no tiene fin. Este tipo de
anualidades se presenta cuando se invierte un capital y únicamente se retiran los intereses; por
tanto, mientras se mantenga invertido el capital, se tendrá una renta perpetua.
Son ejemplos de rentas perpetuas los siguientes:
• Los legados hechos a centros de investigación, organismo de beneficencia, universidades,
etc., que son invertidos y cuyos intereses son utilizados al final de cada periodo.
• Los dividendos provenientes de acciones preferentes de una compañía.
3.1. Valor futuro S de una perpetuidad
Puesto que los pagos de una renta perpetua, en teoría no terminan nunca, es imposible calcular
el valor futuro de los mismos.
3.2. Valor presente P de una perpetuidad
El valor actual de una renta perpetua se encuentra perfectamente definido. Por ejemplo, si una
persona deposita en un banco la cantidad de $50.000, la misma que paga una TEM del 1,5%
mensual, pasado el mes, esta persona puede retirar $750 ($50.000 * 0,015) dejando intacto e
inalterable su capital inicial. Los mismos podría hacer al final del segundo mes, y el capital inicial
sería el mismo, y así sucesivamente. De esto se dice que $50,000 son el valor actual de una renta
perpetua de $750 por mes.
Este tipo de rentas, pueden ser vencidas, anticipadas o diferidas. Sin embargo, las rentas
perpetuas vencidas son las más usadas en el mundo de los negocios. En este punto analizaremos
este tipo de rentas.
Estas rentas las podríamos visualizar a través de la siguiente gráfica:
El valor presente o valor actual de la renta perpetua vencida es aquella cantidad P que, en un
periodo de interés, produce R de intereses. En el ejemplo anterior P son los $50.000 que están
depositados en el banco y R son los $750 que gana dicho deposito en intereses.
Esto es:
P i R
* =
Esto es:
P
R
i
= (1)
P
R R R R
0 1 2 3 4 períodos

197. Cálculo financiero
P R O E S A D
197
Ejemplo 1
Valor presente P de una perpetuidad
Según el testamento del reconocido catedrático Jorge Chang, se establece que deberá
pagarse al Hospital “Mi Buen Jesús”, una renta perpetua de $50.000, pagaderos al final de
cada año. ¿Cuál es el valor actual de ese legado, suponiendo que se encuentra invertido a
una TNA de 18%?
Solución:
Los datos son:
R = $50.000
i = 18%
Reemplazando los valores en la ecuación (1), se tiene:
P
= =
50 000
0 18
277 777 78
.
,
$ . ,
De esto, el valor actual del legado es de $277.777,78, el cual significa que si invertimos
esos $277.777,78 al 18% anual, se generará un interés de $50.000 al año. El Hospital
“Mi Buen Jesús” recibirá por tiempo indefinido este importe, salvo que cambie la tasa de
interés o bien si parte o todo de dicho legado sea retirado. 
Ahora, si en lugar de retirar el interés a medida que se gana, se deja capitalizar por cierto número
de períodos, al final de los cuales se retira el interés compuesto ganado, dejando intacto el
capital inicial, entonces en ese caso tendríamos que hallar el valor actual de una renta perpetua
a pagar al final de cada cierto número de períodos de capitalización.
En este caso, utilizamos la ecuación siguiente:
P
R
i
n
=
+
( ) −
1 1
(2)
Ejemplo 2
Valor presente P de una perpetuidad
Cierta universidad estadounidense recibe semestralmente una donación por $100.000
para otorgar becas para estudios de postgrado a estudiantes latinoamericanos de escaso
recursos económicos. Si la TNA es 25% capitalizable cada mes, determine el valor presente
de la donación
Solución:

198. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
198
Los datos son:
R = $100.000
i = 25%
Reemplazando en la ecuación (2), se tiene:
P =
+





 −
=
100 000
1
0 25
12
1
759 335 40
6
.
,
$ . ,
El valor presente de la donación asciende a $759.335,40. La cantidad que se debe invertir
el hoy al 25% capitalizable mensualmente, con el fin de retirar $100.000 al final de cada
semestre es de $759.335,40. 

199. 199
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Anualidades diferidas
1. La compañía Norteamericana Repsol adquiere unos yacimientos petrolíferos en la selva
peruana; los estudios de ingeniería muestran que los trabajos preparatorios y vías de acceso
demorarán 3 años. Se estima que los yacimientos en explotación rendirán una ganancia
anual de $25.000.000, suponiendo que la TNA es del 7% y que los yacimientos se agotarán
después de 25 años continuos de explotación, hállese el valor futuro de la renta que espera
obtenerse. Rpta. $1.581.225.943
2. Hallar el valor presente de las utilidades que la compañía Repsol obtendrá, al momento de
adquirir los yacimientos de petróleo. Rpta. $237.819.881
3. Una deuda de $800.000 se va a cancelar mediante 20 pagos trimestrales cada uno. Si el
primer pago se efectúa exactamente al año de haberse prestado el dinero, calcular el valor
de cada cuota, aplicando una TNA de 36% capitalizable trimestralmente. Rpta. $113.492,69
4. Una compañía frutera sembró cítricos que empezaran a producir dentro de 5 años. La
producción anual se estima en $400.000 y ese rendimiento se mantendrá por espacio de 20
años. Hallar con la TNA del 6% el valor presente de la producción. Rpta. $3.428.396,90

200. 200
5. La señorita Susy Gonzáles obtiene un préstamo del Banco BBVA por $3.000, el mismo que será
destinado para la compra de una computadora portátil de última generación. El préstamo se
pagará a través de 36 pagos mensuales, después de un período de gracia total (los intereses
no se pagan, si no se capitalizan) de un año. Obtenga el valor del pago mensual sabiendo
que la TNA es del 24% capitalizable cada mes. Rpta. $149,27
Perpetuidades
6. Hallar el valor actual de una perpetuidad de $5.000, cuyo primer pago se hará dentro de 6
meses, con TNA de 12% convertible mensualmente. Rpta. $475.732,84
7. Los exalumnos de una universidad deciden donarle un laboratorio y los fondos para su
mantenimiento futuro. Si el costo inicial de $200.000 y el mantenimiento se estima en
$35.000 anuales, hallar el valor de la donación, si la TNA es del 7%. Rpta. $235.000
8. Encuentre el pago mensual de una perpetuidad cuyo valor presente es de $360,000,
suponiendo una TNA de 25% capitalizable cada mes. Rpta. $7.500
9. Según el testamento del reconocido médico George Anderson, se establece que deberá
pagarse al Hospital “Metropolitano”, una renta perpetua de $10.000, pagaderos al final de
cada año. ¿Cuál es el valor actual de ese legado, suponiendo que se encuentra invertido a
una TNA de 15%? Rpta. $66.666,67
10. El testamento de Don Julio Fabre establece que una parte de sus bienes se invertirán de
modo de Cáritas reciba, a perpetuidad, una renta de $70.000 al inicio de cada año. Si la TNA
es 23% anual, encuentre el valor presente de la donación. Rpta. $374.347,83

201. Cálculo financiero
P R O E S A D
201
10
Sesión
programas de
amortización de
créditos
1. INTRODUCCIÓN
El término amortización tiene origen en la palabra francesa “A mort” que tiene un significado
relacionada con la muerte. Esto sucede debido a que comúnmente los créditos o préstamos que
se contraen se cancelan mediante pagos parciales o abonos. En este caso se dice que el préstamo
se amortiza. De este modo al amortizar una deuda la estamos “matando” o “cancelando”, en
el mejor de las interpretaciones. Por tanto, en el área financiera, amortizar significa saldar
gradualmente una deuda por medio de una serie de pagos que, generalmente, son iguales y
que se realizan también a intervalos de tiempo iguales.
Aunque esta igualdad de pagos y periodicidad es lo más común, también se llevan a cabo
operaciones con algunas variantes. Los pagos que se hacen para amortizar una deuda se aplican
para cubrir los intereses y para reducir el importe de la deuda. Para visualizar este proceso
conviene elaborar una tabla de amortización que muestre lo que sucede con los pagos, los
intereses, la deuda, la amortización y el saldo. Esta se puede definir como un cuadro o tabla
donde se muestra tanto la cantidad pagada de intereses como la cantidad pagada de capital.
La amortización es una de las aplicaciones más importantes de las anualidades.
En efecto, cuando se amortiza una deuda efectuando pagos periódicos iguales, la deuda es
el valor actual de una anualidad, y éste se calcula utilizando la fórmula de valor presente
correspondiente al tipo de anualidad utilizada, vencida o anticipada.
La amortización de una deuda puede ser con interés simple o con interés compuesto. A
continuación veremos cada una de ellas:
2. AMORTIZACIÓN CON INTERÉS SIMPLE
La amortización con interés simple puede llevarse a cabo de dos maneras distintas:
a) Con interés global
b) Con interés sobre saldos insolutos (al rebatir)

202. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
202
2.1. Amortización con interés global
En este tipo de amortización los intereses son calculados sobre el total de la deuda, sin tomar en
cuenta los pagos parciales efectuados.
Ejemplo 1
Amortización con interés global
La señorita Lizbeth Ángeles compra una computadora Pentium IV, marca Toshiba al crédito,
cuyo precio de contado es $4.800, bajo las siguientes condiciones de pago: tasa de interés
global de 48% y 6 meses para pagar dando abonos mensuales iguales en cantidad. Calcule
el valor del abono mensual.
Solución:
Los datos son:
S = ?
P = $4.500
i = 48%
n = 6 meses
En primer lugar calculamos el monto de la deuda, el cual es como sigue:
S = +





 =
4 800 1
0 48
12
6 5 952
.
,
* $ .
Al dividir este monto entre los 6 meses, se obtendrá el valor del abono mensual de $992
(5.952/6). El interés mensual es de 0,48/12 = 0,04.
La tabla de amortización es como sigue:
El valor de cada cuota mensual es $992 y el interés total a pagar por el crédito es $1.152
($5.952 – $4.800). 
Mes Saldo
inicial
Amortización Interés Total
Cuota
Saldo
insoluto
0 4.800 4.800
1 4.800 800 192 992 4.000
2 4.000 800 192 992 3.200
3 3.200 800 192 992 2.400
4 2.400 800 192 992 1.600
5 1.600 800 192 992 800
6 800 800 192 992 0
Total 4.800 1.152 5.952

203. Cálculo financiero
P R O E S A D
203
La amortización de créditos, utilizando el interés global está prohibida en cualquier parte del
mundo por dos razones específicas:
• Es una regla injusta, ya que no bonifica intereses por los abonos efectuados.
• La tasa de interés en realidad es superior a la tasa mencionada.
Así, en el ejemplo anterior, cada pago de $992 se divide en dos partes: $800 ($4.800/6) para
pagar el capital o principal y $192 ($4.800 * (0,48/12)) para el pago de los intereses. Cada mes,
después de realizado un pago, la deuda se reduce en $800, pero el deudor sigue pagando los
mismos intereses; esto hace que en realidad la tasa de interés no sea en realidad de 48%, sino
aumente cada mes. Por ejemplo, después de 3 abonos la deuda se reduce a $2.400 y el interés
sigue siendo de $192; por tanto, la tasa de interés aplicable para el cuarto mes es:
i =
( )( )
=
192
2 400 1
100 12 96
.
* * %
Al momento del último pago, el deudor paga un interés de $192 sobre una deuda de $800. La
tasa de interés realmente aplicada es:
i =
( )( )
=
192
800 1
100 12 288
* * %
Por tanto, en el ejemplo, solo en el primer mes, la casa comercial aplica o cobra una tasa de 48%
anual. Es por esto que este tipo de amortización no está permitido en ningún sistema financiero.
Ejemplo 2
Amortización con interés global
Comercial Ramírez ofrece una videocámara marca Sony, cuyo precio de lista es de $1.500,
bajo las siguientes condiciones de pago: tasa de interés global de 3% mensual y 10 cuotas
mensuales de igual cantidad. Calcule el valor del abono mensual.
Solución:
Los datos son:
S = ?
P = $1.500
i = 3%
n = 10 meses
En primer lugar calculamos el monto de la deuda, el cual es como sigue:
S = +

 
 =
1 500 1 0 03 10 1 950
. , * $ .

204. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
204
Al dividir este monto entre los 10 meses, se obtendrá el valor del abono mensual de $195
(1.950/10).
La tabla de amortización es como sigue:
El valor de cada cuota mensual es $195. 
2.2. Amortización con interés sobre saldos insolutos (al rebatir)
Lo insoluto significa lo no pagado, entonces el saldo insoluto de una deuda en un momento dado
es el saldo de deuda vigente a ese momento, conformado por el capital insoluto (capital impago,
capital no amortizado o capital “vivo”) vigente y la totalidad de los intereses devengados y no
pagados hasta ese momento, de acuerdo a la modalidad de crédito. De esta manera en este
tipo de amortización los intereses son calculados sobre el saldo de la deuda, a diferencia de la
amortización utilizando el interés global, donde los intereses son calculados sobre el total de la
deuda.
Es necesario mencionar la diferencia que existe entre amortización y abono. Amortización, como
se ha mencionado, significa liquidar el capital mediante una serie de pagos, generalmente iguales,
mientras que el abono o pago total es la suma de la amortización más el interés generado en
el período.
Ejemplo 1
Amortización con interés sobre saldos insolutos (al rebatir)
La señorita Lizbeth Ángeles compra una computadora Pentium IV, marca Toshiba al crédito,
cuyo precio de contado es $4,800, bajo las siguientes condiciones de pago: tasa de interés
sobre saldos insolutos o al rebatir de 48% y 6 meses para pagar. Calcule el importe de los
intereses en cada período y de la cuota periódica.
Mes Saldo
inicial
Amortización Interés Total
Cuota
Saldo
insoluto
0 1.500 1.500
1 1.500 150 45 195 1.350
2 1.350 150 45 195 1.200
3 1.200 150 45 195 1.050
4 1.050 150 45 195 900
5 900 150 45 195 750
6 750 150 45 195 600
7 600 150 45 195 450
8 450 150 45 195 300
9 300 150 45 195 150
10 150 150 45 195 0
Total 1.500 450 1.950

205. Cálculo financiero
P R O E S A D
205
Mes Saldo
inicial
Amortización Interés Total
Cuota
Saldo
insoluto
0 4.800 4.800
1 4.800 800 192 992 4.000
2 4.000 800 160 960 3.200
3 3.200 800 128 928 2.400
4 2.400 800 96 896 1.600
5 1.600 800 64 864 800
6 800 800 32 832 0
Total 4.800 672 5.472
Solución:
R = ?
P = $4.800
i = 48%
n = 6 meses
En nuestro caso, la amortización mensual es $800 (4.800/6). Los intereses mensuales
se deben calcular sobre la parte no pagada del capital (saldo insoluto) que va quedando
después de cada amortización. En nuestro ejemplo, desde el inicio hasta el final del primer
mes, el saldo insoluto es de $4,800. por tanto, el interés a pagar al efectuar el primer
abono será:
I
= =
4 800
0 48
12
1 192
. *
,
* $
Al final del primer mes se tendrá que pagar $800 de amortización y $192 de intereses; es
decir, se tendrá que dar un abono de $992.
El saldo insoluto al inicio del segundo mes es de $4.000 (4.800 – 800). Los intereses a
pagar al final del segundo mes será:
I
= =
4 000
0 48
12
1 160
. *
,
* $
Al final del segundo mes se tendrá que abonar $960 (800 + 160). Y así se procede con los
meses o períodos que siguen.
La tabla de amortización es como sigue:
El precio total pagado por la computadora es de $5.472, de los cuales $4.800 corresponden
al capital y $672 a los intereses. De este ejemplo se puede observar que los intereses
cobrados aplicados sobre saldos absolutos es menor que el cobrado mediante el interés
global. A su vez, se observa que los pagos totales son cada vez menores, esto debido a
que los intereses van decreciendo; sin embargo, en la práctica la cuota total es igual cada
mes. En nuestro ejemplo, el pago total mensual constante, con intereses incluidos, es de:
$5.472 / 6 = $912. 

206. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
206
Ahora, sucede que en las operaciones a crédito de mediano y largo plazo, el cálculo del pago
constante, sea éste semanal, quincenal, mensual, etc., se convierte en un trabajo demasiado
laborioso y tardío. Por ello, para hallar el interés total sobre saldos insolutos, se puede aplicar la
ecuación siguiente:
S R
i
i
n
=
+
( ) −








*
1 1
(1)
En la ecuación a es el monto de la amortización.
Ejemplo 2
Amortización con interés sobre saldos insolutos (al rebatir)
Utilice la ecuación (1) para calcular el abono mensual constante en el ejemplo anterior.
Solución:
Los datos son:
R = ?
P = $4.800
a = $800
i = 48%
n = 6 meses
Sustituyendo los valores en la ecuación (1), tenemos:
I = +
( ) =
6
0 48
12
2
4 800 800 672
*
,
. $
Ahora, para hallar el abono mensual, sumamos el valor de contado de la computadora
($4.800) más los intereses ($672) y lo dividimos entre el número de cuotas.
Abono
monto
n
S
n
= = =
+
=
4 800 672
6
912
.
$
Para pagar la computadora, el cliente deberá abonar seis cuotas mensuales de $912 cada
una. 
3. AMORTIZACIÓN CON INTERÉS COMPUESTO
Dentro de este tipo de amortización, tenemos una gran variedad, las cuales son usadas por
distintas instituciones financieras. Veamos cada uno de ellas.

207. Cálculo financiero
P R O E S A D
207
3.1. Sistema de amortización constante (método alemán)
Este tipo de amortización es también conocido como plan de amortizaciones al rebatir, donde los
intereses son calculados sobre el saldo de la deuda. Asimismo, a este sistema de amortización
se le conoce como sistema de pagos decrecientes, esto debido a que como los saldos insolutos
disminuyen, las cuotas de interés también disminuyen. A continuación, mostraremos algunos
ejemplos.
Ejemplo
Sistema de amortización constante (método alemán)
Una empresa recibe un préstamo del BWS para la construcción de la nueva planta de
producción por $100.000. El préstamo será cancelado en 10 cuotas mensuales. El banco
aplica una TEA de 34,48%. Calcular el valor de la cuota mensual.
Solución:
Los datos son:
P = $100.000
i = 34,48%
n = 10 meses
La amortización mensual es de $10.000 (100.000/10). A continuación calculamos el
interés mensual, el mismo que será utilizado en la tabla de amortización.
i = + − =
1 0 3448 1 2 5
12
, , %
La tabla de amortización es como sigue:
Se observa en la tabla que la amortización es constante y por tanto las cuotas son
decrecientes. 
Mes Saldo
inicial
Amortización Interés Total
Cuota
Saldo
insoluto
0 100.000 100.000,00
1 100.000 10.000 2.500 12.500 90.000
2 90.000 10.000 2.250 12.250 80.000
3 80.000 10.000 2.000 12.000 70.000
4 70.000 10.000 1.750 11.750 60.000
5 60.000 10.000 1.500 11.500 50.000
6 50.000 10.000 1.250 11.250 40.000
7 40.000 10.000 1.000 11.000 30.000
8 30.000 10.000 750 10.750 20.000
9 20.000 10.000 500 10.500 10.000
10 10.000 10.000 250 10.250 0
Total 100.000 13.750 113.750

208. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
208
3.2. Sistema de amortización única al vencimiento (método americano
simple)
Este sistema de amortización se caracteriza por:
a) Solo se realiza una amortización de capital al vencimiento del préstamo, por el total del
mismo.
b) En las demás cuotas periódicas tan sólo se pagan los intereses del periodo.
Ejemplo
Sistema de amortización única al vencimiento (método americano simple)
Una empresa recibe un préstamo del BWS para la construcción de la nueva planta de
producción por $100.000. El préstamo será cancelado en 10 cuotas mensuales. El banco
aplica una TEA de 34,48%. Calcule el importe de los intereses en cada período y de la cuota
periódica.
Solución:
La amortización es única al vencimiento, por tanto en los meses previos solo se paga
intereses. A continuación calculamos el interés mensual, el mismo que será utilizado en la
tabla de amortización.
i = + − =
1 0 3448 1 2 5
12
, , %
En seguida, calculamos el interés mensual:
I = +
( ) −

 
 =
100 000 1 0 025 1 2 500
. * , $ .
La tabla de amortización es como sigue:
Mes Saldo inicial Amortización Interés Total Cuota Saldo insoluto
0 100.000,00 100.000,00
1 100.000,00 2.500,00 2.500,00 100.000,00
2 100.000,00 2.500,00 2.500,00 100.000,00
3 100.000,00 2.500,00 2.500,00 100.000,00
4 100.000,00 2.500,00 2.500,00 100.000,00
5 100.000,00 2.500,00 2.500,00 100.000,00
6 100.000,00 2.500,00 2.500,00 100.000,00
7 100.000,00 2.500,00 2.500,00 100.000,00
8 100.000,00 2.500,00 2.500,00 100.000,00
9 100.000,00 2.500,00 2.500,00 100.000,00
10 100.000,00 100.000,00 2.500,00 2.500,00 0,00
Total 100.000,00 25.000,00 125.000,00

209. Cálculo financiero
P R O E S A D
209
Mes Saldo inicial Amortización Interés Total Cuota Saldo insoluto
0 100.000,00 100.000,00
1 100.000,00 8.925,88 2.500,00 11.425,88 91.074,12
2 91.074,12 9.149,02 2.276,85 11.425,88 81.925,10
3 81.925,10 9.377,75 2.048,13 11.425,88 72.547,35
4 72.547,35 9.612,19 1.813,68 11.425,88 62.935,16
5 62.935,16 9.852,50 1.573,38 11.425,88 53.082,66
6 53.082,66 10.098,81 1.327,07 11.425,88 42.983,85
7 42.983,85 10.351,28 1.074,60 11.425,88 32.632,57
8 32.632,57 10.610,06 815,81 11.425,88 22.022,51
9 22.022,51 10.875,31 550,56 11.425,88 11.147,20
10 11.147,20 11.147,20 278,68 11.425,88 0,00
Total 100.000,00 14.258,76 114.258,76
Se observa en la tabla que la amortización es al final y, por tanto, en los períodos previos
sólo se paga intereses. 
3.3. Sistema de pagos constantes (método francés)
Este sistema se caracteriza por tener cuotas o abonos de amortización constantes a lo largo
de la vida del préstamo. El interés que se aplica es sobre los saldos insolutos de la deuda en
un período, es decir los pagos totales R, se calculan a partir de la fórmula de anualidades, y
dichos pagos incluyen una parte de capital y otra de intereses. Este tipo de amortización es muy
utilizado por los bancos, financieras, tiendas comerciales y negocios que venden al crédito.
Para hallar el valor de cada una de las rentas constantes, utilizamos el factor de recuperación del
capital (FRC).
Ejemplo
Sistema de pagos constantes (método francés)
Una empresa recibe un préstamo del BWS para la construcción de la nueva planta de
producción por $100.000. El préstamo será cancelado en 10 cuotas mensuales. El banco
aplica una TEA de 34,48%. Calcule el valor de la cuota mensual.
Solución:
Primeramente tenemos que encontrar la tasa efectiva mensual, el cual es como sigue:
i = + − =
1 0 3448 1 2 5
12
, , %
Sustituyendo los valores en la ecuación de FRC, tenemos:
R =
( ) +
( )
+
( ) −








=
100 000
0 025 1 0 025
1 0 025 1
11 425 8
10
10
.
, ,
,
$ . , 8
8
La tabla de amortización es como sigue:

210. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
210
Se observa en la tabla que las cuotas mensuales son iguales. 
3.4. Sistema de pagos con período de gracia
En el capítulo anterior abordamos el tema de anualidades diferidas, en ella señalábamos que
es aquella cuyo plazo comienza hasta después de transcurrido un cierto intervalo de tiempo
desde el momento en que la operación quedó formalizada. Asimismo, se había dicho que a ese
intervalo de tiempo que transcurre entre el momento inicial y el inicio del plazo de la anualidad
se llama período de gracia o período de diferimiento, donde puede suceder una de las dos
situaciones siguientes:
1) Que al final de cada período de pago se liquiden o paguen los intereses generados por el
capital original. Es este caso estamos hablando de un período de gracia normal o parcial.
2) Que los intereses generados dentro del período de gracia se capitalicen. En este caso, esta-
mos frente a un período de gracia total.
A continuación, veremos algunos ejemplos de amortización de créditos utilizando periodo de
gracia normal y periodo de gracia total.
Ejemplo 1
Sistema de pagos con períodos de gracia
Una empresa recibe un préstamo del BWS para la construcción de la nueva planta de
producción por $100.000. El préstamo será cancelado en 10 cuotas mensuales. El banco
aplica una TEA de 34,48%. Se sabe que el banco nos concede dos períodos de gracia, el
primero parcial y el segundo total. Calcule el valor de la cuota mensual.
Solución:
Primeramente tenemos que encontrar la tasa efectiva mensual, el cual es como sigue:
i = + − =
1 0 3448 1 2 5
12
, , %
Luego, como se obtiene dos períodos de gracia, uno normal y otro total, entonces
calculamos los intereses que se tendrá que abonar solo en el primer período, dado que
el primer período de gracia es normal. Los intereses generados por el préstamo y se
abonarán en el primer mes, asciende a:
I = +
( ) −

 
 =
100 000 1 0 025 1 2 500
. , $ .
Ahora, dado que hemos recibido para el segundo mes un período de gracia total, al final
del mes dos, mi deuda asciende a $102.500 y ya no los $100.000, debido a que los
intereses se capitalizaron.
Una vez terminado los dos el períodos de gracia, mi deuda asciende a $102.500 y a
continuación calculo el valor de cada cuota, utilizando la ecuación del FRC:

211. Cálculo financiero
P R O E S A D
211
R =
( ) +
( )
+
( ) −








=
102 500
0 025 1 0 025
1 0 025 1
14 295 40
8
8
.
, ,
,
$ . ,
La tabla de amortización es como sigue:
Se observa en la tabla que las cuotas mensuales son iguales a partir del período tres. 
Ejemplo 2
Sistema de pagos con períodos de gracia
Una empresa recibe un préstamo del BWS para la construcción de la nueva planta de
producción por $100.000. El préstamo será cancelado en 10 cuotas mensuales. El banco
aplica una TEA de 34,48%. Se sabe que el banco nos concede dos períodos de gracia total.
Calcule el valor de la cuota mensual.
Solución:
Primeramente tenemos que encontrar la tasa efectiva mensual, el cual es como sigue:
i = + − =
1 0 3448 1 2 5
12
, , %
Ahora, como en este caso se obtiene dos períodos de gracia total, calculamos los intereses
generados para cada uno de los períodos de gracia que no se abonaron.
De esto, los intereses generados en el primer periodo de gracia será:
I = +
( ) −

 
 =
100 000 1 0 025 1 2 500
. , $ .
Sin embargo, como dichos intereses no se cancelaron al final del período uno, entonces mi
deuda no sigue siendo la misma, sino que se incrementa a $102.500.
Mes Saldo inicial Amortización Interés Total Cuota Saldo insoluto
0 100.000,00 100.000,00
1 100.000,00 2.500,00 2.500,00 100.000,00
2 100.000,00 102.500,00
3 102.500,00 11.732,90 2.562,50 14.295,40 90.767,10
4 90.767,10 12.026,23 2.269,18 14.295,40 78.740,87
5 78.740,87 12.326,88 1.968,52 14.295,40 66.413,99
6 66.413,99 12.635,05 1.660,35 14.295,40 53.778,94
7 53.778,94 12.950,93 1.344,47 14.295,40 40.828,01
8 40.828,01 13.274,70 1.020,70 14.295,40 27.553,30
9 27.553,30 13.606,57 688,83 14.295,40 13.946,73
10 13.946,73 13.946,73 348,67 14.295,40 0,00
Total 102.500,00 14.363,22 116.863,22

212. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
212
Los intereses generados en el segundo período, que tampoco se abonaron, asciende a:
I = +
( ) −

 
 =
102 500 1 0 025 1 2 562 50
. , $ . ,
Luego de calcular ambos intereses que no se abonaron, nuestra deuda asciende al final del
período dos a $105.062.50. Por tanto, una vez terminado los dos períodos de gracia, mi
deuda asciende a $105.062.50 y a continuación calculo el valor de cada cuota, utilizando
la ecuación del FRC:
R =
( ) +
( )
+
( ) −








=
105 062 50
0 025 1 0 025
1 0 025 1
14 652
8
8
, ,
, ,
,
$ . ,7
79
La tabla de amortización es como sigue:
Se observa en la tabla que las cuotas mensuales son iguales a partir del período tres. 
3.5. Sistema de pagos VAC (valor de actualización constante)
Este tipo de amortización se caracteriza porque las cuotas aumentan en forma sucesiva a través
del tiempo. Esto es así debido a que la tasa pactada se ajusta debido a la inflación.
Este sistema, tiene las siguientes características:
a) El capital se ajusta según el período de conversión, de acuerdo al "índice de ajuste" que se
ha definido o acordado.
b) El interés se calcula sobre el saldo de la deuda ajustada.
c) La tasa de interés establecida es baja, pero se complementa con el índice de ajuste de
capital.
d) El cálculo del pago de la deuda se hace en base al número de períodos que faltan por vencer.
Mes Saldo inicial Amortización Interés Total Cuota Saldo insoluto
0 100.000,00 100.000,00
1 100.000,00 102.500,00
2 102.500,00 105.062,50
3 105.062,50 12.026,23 2.626,56 14.652,79 93.036,27
4 93.036,27 12.326,88 2.325,91 14.652,79 80.709,39
5 80.709,39 12.635,05 2.017,73 14.652,79 68.074,34
6 68.074,34 12.950,93 1.701,86 14.652,79 55.123,41
7 55.123,41 13.274,70 1.378,09 14.652,79 41.848,71
8 41.848,71 13.606,57 1.046,22 14.652,79 28.242,14
9 28.242,14 13.946,73 706,05 14.652,79 14.295,40
10 14.295,40 14.295,40 357,39 14.652,79 0,00
Total 105.062,50 12.159,80 117.222,30

213. Cálculo financiero
P R O E S A D
213
Ejemplo
Sistema de pagos VAC (valor de actualización constante)
Una empresa recibe un préstamo del BWS para la construcción de la nueva planta de
producción por $100.000. El préstamo será cancelado en 10 cuotas mensuales. El banco
aplica una TEA de 34,48%. Asimismo, el interés será ajustado de acuerdo al IPC, el mismo
que se proyecta a 2% mensual. Calcule el valor de la cuota mensual.
Solución:
Primeramente tenemos que encontrar la tasa efectiva mensual, el cual es como sigue:
i = + − =
1 0 3448 1 2 5
12
, , %
Según este sistema, el cálculo de la cuota se efectúa sobre el saldo de la deuda ajustada.
Por tanto, para calcular la primera cuota se tiene:
R =
+
( )
+
( ) −








=
102 000
0 025 1 0 025
1 0 025 1
11 654 39
10
10
.
, ,
,
$ . ,
Para la segunda cuota:
R =
+
( )
+
( ) −








=
94 753 52
0 025 1 0 025
1 0 025 1
11 887 48
9
9
. ,
, ,
,
$ . ,
Para la tercera cuota:
R =
+
( )
+
( ) −








=
86 939 57
0 025 1 0 025
1 0 025 1
12 125 23
8
8
. ,
, ,
,
$ . ,
La tabla de amortización es como sigue:
Se observa en la tabla que las cuotas mensuales aumentan debido al ajuste por inflación. 
Mes Saldo
inicial
Saldo
ajustado
Amortización Interés Total
cuota
Saldo
insoluto
0 100.000,00 100.000,00
1 100.000,00 102,000.00 9,104.39 2,550.00 11,654.39 92,895.61
2 92,895.61 94,753.52 9,518.64 2,368.84 11,887.48 85,234.87
3 85,234.87 86,939.57 9,951.74 2,173.49 12,125.23 76,987.83
4 76,987.83 78,527.59 10,404.55 1,963.19 12,367.74 68,123.04
5 68,123.04 69,485.50 10,877.95 1,737.14 12,615.09 58,607.55
6 58,607.55 59,779.70 11,372.90 1,494.49 12,867.39 48,406.80
7 48,406.80 49,374.93 11,890.37 1,234.37 13,124.74 37,484.57
8 37,484.57 38,234.26 12,431.38 955.86 13,387.24 25,802.88
9 25,802.88 26,318.94 12,997.01 657.97 13,654.98 13,321.93
10 13,321.93 13,588.37 13,588.37 339.71 13,928.08 0,00
Total 112,137.30 15,475.06 127,612.36

214. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
214
4. COSTO EFECTIVO DEL CRÉDITO
Hasta aquí, hemos visto algunos sistemas de amortización de créditos, donde lo que se cobra por
éstos, son tan sólo los intereses. Sin embargo, esto no es así en la práctica, es por ello que cuando
una persona solicita un crédito cualquiera a un banco, no solo se debe concentrar en la tasa de
interés, sino además de éste se debe informar bien y preguntar sobre todas las comisiones y
portes que se sumarán al pago de intereses y el principal que se efectuará mensualmente.
Ante esto surge la pregunta del millón: ¿Qué le puede cobrar el banco, además de la tasa
de interés? Al respeto la Superintendencia de Banca y Seguros (SBS) publica periódicamente
información sobre los costos asociados a los créditos de consumo que ofrecen los bancos del
sistema, donde se puede observar los siguientes:
a) Seguro de desgravamen: este seguro protege a la entidad bancaria en caso de fallecimiento
del cliente deudor. Este seguro cubre el total de la deuda vigente, que no se encuentre en
situación morosa, a la fecha de fallecimiento del cliente, siendo de cargo de sus herederos
los intereses, comisiones, capital y gastos de préstamos en mora y que no se hayan pagado
hasta dicha fecha. En algunos bancos este seguro se aplica sobre el saldo pendiente de pago,
salvo en los casos del BBVA Continental y del Trabajo, donde se cobra sobre el monto finan-
ciado. Asimismo, este tipo seguro, también es cobrado en los créditos a través de las tarjetas,
así como en los créditos hipotecarios.
b) Portes: algunos bancos lo denominan gastos administrativos. Son aquellos cobros por el
servicio de consulta de saldos, últimos movimientos, cartas y/o comunicados que envían las
empresas del sistema financiero.
c) Comisiones: los bancos también cobran comisiones, la más conocida de ellas es la comisión
de desembolso, que no es otra cosa que un importe que el banco cobra por desembolsar el
préstamo, ya sea éste al momento de desembolsar el dinero o si se financia.
d) Capitalización de los intereses: también hay considerar la frecuencia en que los bancos y
financieras capitalizan los intereses, dado que no es lo mismo que los intereses se capitalizan
de manera bimestral, mensual, quincenal o diariamente. Recordemos que mientras muchas
más veces se capitalizan los intereses en un año, estos son mayores.
Como se dijo anteriormente, en la práctica, las entidades financieras aparte de la tasa de interés
que anuncia nos cobra otros tipos de conceptos, lo que encarece el costo del crédito. En otras
palabras, un banco me podría ofrecer un préstamo al 20% anual cuando en realidad estoy
pagando un 24%, esto por cobros de portes, comisiones, seguros, etc. Por ejemplo, supongamos
que recibimos un préstamo de $100 a una tasa de 10%, asimismo, el banco nos cobra una
comisión de desembolso del 1% del préstamo. ¿Cuál es el costo efectivo del préstamo?
i = −





 =
110
99
1 100 11 11
* . %
De lo anterior, podemos expresar que el costo efectivo está dado por la corriente de efectivo del
préstamo. En otras palabras el costo efectivo está dada por lo que efectivamente recibí y lo que
efectivamente pagué.

215. Cálculo financiero
P R O E S A D
215
4.1. Uso del VAN y la TIR en la evaluación de crédito
Antes de pasar a ver algunos ejemplos, es importante definir a dos herramientas importantes en
la evaluación de créditos: el valor actual neto (VAN) y la tasa interna de rendimiento (TIR), los
cuales nos permitirán calcular el costo efectivo de un crédito.
Valor actual neto (VAN)
El valor actual (VA) de una inversión se define como el valor actualizado de la corriente de los
flujos de caja que ella promete generar a lo largo de su vida. Para actualizar todos los flujos de
caja utilizamos una tasa de descuento, denominada costo de capital o costo de oportunidad del
capital empleado en el proyecto de inversión.
El valor actual neto (VAN), es todo lo anterior, menos el valor del desembolso inicial o inversión
inicial, de ahí el nombre de valor actual neto (VAN).
La expresión general del cálculo del VAN es la siguiente:
VAN P
R
i
R
i
R
i
R
i
R
i
n
n
= − +
+
( )
+
+
( )
+
+
( )
+
+
( )
+ +
+
( )


1
1
2
2
3
3
4
4
1 1 1 1 1
....







(2)
En la ecuación, P es el desembolso inicial o la inversión inicial.
Tasa interna de retorno (TIR)
Se denomina tasa interna de retorno (TIR) a la tasa de descuento i para la que un crédito
bancario tendría un VAN igual a cero. La TIR es, pues, una medida de la rentabilidad relativa de
una inversión.
Podríamos definir la TIR con mayor propiedad si decimos que es la tasa rentabilidad del
prestamista: banco o financiera. Para la empresa o persona natural la TIR representa el costo
efectivo del crédito.
Entre varias propuestas de bancos o financieras, se deberá elegir aquel que presente la TIR más
baja.
Ahora, cuando el banco o financiera solo me cobra la tasa de interés que anuncia, el valor del
VAN = 0. Sin embargo, esto no sucede en la práctica. De esta manera, el VAN generalmente será
mayor a cero. Por tanto, entre varias propuestas de bancos o financieras, se deberá elegir aquel
que presente el VAN más baja.
De esto se deduce que:
a) Cuando el VAN = 0, entonces la tasa de interés que me cobra el banco es igual al costo
efectivo del crédito. Por tanto, la tasa de interés es igual a la TIR.
b) Cuando el VAN > 0, entonces la tasa de interés que me cobra el banco es menor al costo
efectivo del crédito. Por tanto, la tasa de interés es menor a la TIR.

216. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
216
Ejemplo 1
Costo efectivo del crédito
Se obtiene un préstamo del Banco de Crédito por $3.000 a pagar en cinco meses. El banco
aplica una TEM de 2,5%. Calcule el valor de la cuota o abono mensual, así como el costo
efectivo del préstamo.
Solución:
Los datos son:
R = ?
P = $3.000
i = 2,5%
n = 5 meses
Sustituyendo los valores en la ecuación (1), tenemos:
R =
+
( )
+
( ) −








3 000
0 025 1 0 025
1 0 025 1
5
5
. *
, ,
,
R = $ ,
645 74
La tabla de amortización es como sigue:
Para calcular el costo efectivo, nos concentramos en lo que efectivamente recibí; en nuestro
caso $3.000 y lo que efectivamente pagué; una corriente de efectivo de $645,74 por cinco
meses.
Ahora, para hallar el costo efectivo del préstamo utilizamos la ecuación del VAN, que es
la diferencia entre el valor actual de los pagos o abonos efectuados, menos el préstamo.
Mes Saldo
inicial
Amortización Interés Total
Cuota
Saldo
insoluto
0 3.000,00 3.000,00
1 3.000,00 570,74 75,00 645,74 2.429,26
2 2.429,26 585,01 60,73 645,74 1.844,25
3 1.844,25 599,63 46,11 645,74 1.244,62
4 1.244,62 614,63 31,12 645,74 629,99
5 629,99 629,99 15,75 645,74 0,00
Total 3.000,00 228,70 3.228,70

217. Cálculo financiero
P R O E S A D
217
Sustituyendo los valores en la ecuación del VAN se tiene:
VAN
i i i
= − +
+
( )
+
+
( )
+
+
( )
+
+
3 000
645 74
1
645 74
1
645 74
1
645 74
1
1 2 3
.
, , , ,
i
i i
( )
+
+
( )








4 5
645 74
1
,
De esta manera, para hallar el costo efectivo del préstamo, buscamos aquella tasa de
interés i que hace al VAN = 0.
En nuestro caso, como al préstamo solo se le está cargando la tasa de interés mensual de
2,5%, entonces el costo efectivo del préstamo, o aquella tasa de interés i que hace al VAN
= 0, es la misma tasa de interés de 2,5% mensual.
Comprobando se tiene:
VAN = − +
( )
+
( )
+
( )
+
3 000
645 74
1 025
645 74
1 025
645 74
1 025
64
1 2 3
.
,
,
,
,
,
,
5
5 74
1 025
645 74
1 025
0
4 5
,
,
,
,
$
( )
+
( )








=
El costo efectivo del préstamo es de 2,5% mensual. En este caso la tasa que me cobra el
banco es la misma tasa que se anuncia. 
Ejemplo 2
Costo efectivo del crédito
Se obtiene un préstamo del Banco de Crédito por $3.000 a pagar en cinco meses. El banco
aplica una TEM de 2,5%. Asimismo, el banco cobra mensualmente por portes y seguro
$5 y $8 respectivamente. Calcule el valor de la cuota o abono mensual, así como el costo
efectivo del préstamo.
Solución:
Sustituyendo los valores en la ecuación (1), tenemos:
R =
+
( )
+
( ) −








3 000
0 025 1 0 025
1 0 025 1
5
5
. *
, ,
,
R = $ ,
645 74

218. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
218
La tabla de amortización es como sigue:
De la misma manera, para hallar el costo efectivo del préstamo utilizamos la ecuación
del VAN, que es la diferencia entre el valor actual de los pagos o abonos efectuados –
considerando portes y seguros–, menos el préstamo.
En el ejemplo, sería:
VAN
i i i
= − +
+
( )
+
+
( )
+
+
( )
+
+
3 000
658 74
1
658 74
1
658 74
1
658 74
1
1 2 3
.
, , , ,
i
i i
( )
+
+
( )








4 5
658 74
1
,
En este caso, como al préstamo, a parte de los intereses, se le está cargando los portes y
el seguro de desgravamen, entonces el costo efectivo del préstamo ya no solo es el 2,5%
mensual, sino más.
Para hallar el costo efectivo del préstamo, buscamos aquella tasa de interés i que hace al
VAN = 0, y para calcular esa tasa i, tenemos tres métodos: (1) una calculadora financiera,
(2) hoja de cálculo Microsoft Excel y (3) prueba y error. Veamos cada uno de ellos:
Utilizando la calculadora financiera FC-100:
Utilizando la hoja de cálculo Excel:
Mes Saldo
inicial
Amortización Interés Total Portes y
Seguros
Total
Cuota
Saldo
insoluto
0 3.000,00 3.000,00
1 3.000,00 570,74 75,00 645,74 13,00 658,74 2.429,26
2 2.429,26 585,01 60,73 645,74 13,00 658,74 1.844,25
3 1.844,25 599,63 46,11 645,74 13,00 658,74 1.244,62
4 1.244,62 614,63 31,12 645,74 13,00 658,74 629,99
5 629,99 629,99 15,75 645,74 13,00 658,74 0,00
Total 3.000,00 228,70 3.228,70 65,00 3.293,70
Operación Pantalla
MODE 4, MODE 5, 2 SHIFT AC 0.00
3000 +/- CFj -3000.00
658.74 CFj ; 5 Nj 5.00
IRR 3.20
NPV 0.00

219. Cálculo financiero
P R O E S A D
219
La entrada de la celda B8 es =TIR(B2:B7).
Utilizando prueba y error:
Asimismo, la TIR se puede calcular por prueba y error. Puesto que el VAN con un costo de
2,50% es igual a $60,39, podemos probar con tasas más altas hasta converger hacia un
VAN de cero. Con VAN al 3% = $16,84. Con VAN al 3,50% = –$25,75. Entonces la tasa que
hace que el VAN sea cero está entre 3% y 3,50%. Por tanto, la TIR es del 3,20%.
Podemos observar que empleando cualquiera de las tres herramientas, la tasa i que hace
al VAN = 0 es 3,20% mensual. Ahora, si queremos comprobar dicha tasa, reemplazamos
en la fórmula del VAN:
VAN = − +
( )
+
( )
+
( )
+
3 000
658 74
1 032
658 74
1 032
658 74
1 032
65
1 2 3
.
,
,
,
,
,
,
8
8 74
1 032
658 74
1 032
0
4 5
,
,
,
,
$
( )
+
( )








=
El costo efectivo del préstamo es de 3,2% mensual. En este caso la tasa que me cobra
el banco, no es la misma tasa que se anuncia, debido a los costos de portes y seguro de
desgravamen. 
Ejemplo 3
Costo efectivo del crédito
Se obtiene un préstamo del Banco de Crédito por $3.000 a pagar en cinco meses. El banco
aplica una tasa de interés del 2,5% mensual. Asimismo, el banco cobra mensualmente
por portes y seguro $5 y $8 respectivamente y una comisión por desembolsar el crédito
de $100. Calcule el valor de la cuota o abono mensual, así como el costo efectivo del
préstamo.
Solución:
Sustituyendo los valores en la ecuación (1), tenemos:
R =
+
( )
+
( ) −








3 000
0 025 1 0 025
1 0 025 1
5
5
. *
, ,
,
R = $ ,
645 74

220. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
220
La tabla de amortización es como sigue:
Ahora, para hallar el costo efectivo del préstamo, nos concentramos en lo que efectivamente
recibimos y lo que efectivamente pagamos. En nuestro caso, la empresa recibe solo $2.900,
debido a que el banco nos cobró una comisión por desembolsar el préstamo de $100.
La ecuación del VAN, es como sigue:
VAN
i i i
= − +
+
( )
+
+
( )
+
+
( )
+
+
2 900
658 74
1
658 74
1
658 74
1
658 74
1
1 2 3
.
, , , ,
i
i i
( )
+
+
( )








4 5
658 74
1
,
En este caso, como al préstamo, a parte de los intereses, se le está cargando portes, seguro
de desgravamen y una comisión de desembolso, entonces el costo efectivo del préstamo
ya no sólo es el 2,5% mensual, si no mas.
Lo mismo, para hallar el costo efectivo del préstamo, buscamos aquella tasa de interés i
que hace al VAN = 0. Utilizando Excel se tiene:
La entrada de la celda B8 es =TIR(B2:B7).
Se observa que aquella tasa i que hace al VAN = 0 es de 4,40% mensual.
Reemplazando en la fórmula del VAN, tenemos:
VAN = − +
( )
+
( )
+
( )
+
2 900
658 74
1 044
658 74
1 044
658 74
1 044
65
1 2 3
.
,
,
,
,
,
,
8
8 74
1 044
658 74
1 044
0
4 5
,
,
,
,
$
( )
+
( )








=
El costo efectivo del préstamo se elevó de 3,2% a 4,4% mensual, debido a que el banco
me está cobrando una comisión por desembolsar el crédito requerido. Por tanto, la tasa
que me cobra el banco, no es la misma tasa que se anuncia, debido a los costos de portes,
seguro de desgravamen y comisiones. 
Mes Saldo
inicial
Amortización Interés Total Portes y
Seguros
Comisión Total
Cuota
Saldo
insoluto
0 3.000,00 100,00 3.000,00
1 3.000,00 570,74 75,00 645,74 13,00 658,74 2.429,26
2 2.429,26 585,01 60,73 645,74 13,00 658,74 1.844,25
3 1.844,25 599,63 46,11 645,74 13,00 658,74 1.244,62
4 1.244,62 614,63 31,12 645,74 13,00 658,74 629,99
5 629,99 629,99 15,75 645,74 13,00 658,74 0,00
Total 3.000,00 228,70 3.228,70 65,00 100,00 3.293,70

221. 221
¿?¿?
¿?
GLOSARIO DE TÉRMINOS
Anota las palabras que no son comunes en tu vocabulario y busca el significado en un diccionario.
1. ______________ _____________________________________________
2. ______________ _____________________________________________
3. ______________ _____________________________________________
4. ______________ _____________________________________________
5. ______________ _____________________________________________
6. ______________ _____________________________________________
7. ______________ _____________________________________________
8. ______________ _____________________________________________
9. ______________ _____________________________________________
10. ______________ _____________________________________________
PRÁCTICA DIRIGIDA
REFUERZA LAS COMPETENCIAS A LOGRAR
Tú decides si ser el mejor o el peor.
Amortización con interés simple
1. Automotors anuncia en el diario El Comercio, que se puede adquirir un auto Mercedes Benz,
dando una cuota inicial del 40% y el resto a pagar en 10 mensualidades con 5% mensual
de interés global. Si el automóvil cuesta $115.000, obtenga el abono mensual y calcule el
interés que se está pagando por el crédito.
2. Carlos Gamarra debe $2.160, los cuales pagará en 6 pagos mensuales. Los intereses serán
calculados sobre saldos insolutos a la tasa de interés simple del 3,5% mensual. Elabore la
tabla de amortización.
3. Suponga que, en ejemplo anterior, se aplica un 3,5% de interés global. Elabore la tabla de
amortización.
4. Un DVD se puede comprar al contado en $2.540. A crédito se requiere un pago inicial de
$540. Si se cobra una tasa de interés simple global de 44% y la deuda se liquida en 12 pagos
semanales, ¿cuál será el valor de cada pago?
5. Calcular el valor de cada pago suponiendo que, en el ejemplo anterior, el interés aplicado es
sobre saldos insolutos.

222. 222
Amortización con interés compuesto
6. La empresa Los Amigos S.A.C., recibe un préstamo del Banco Intesa por $10,000 a pagar
en tres años, los cuales se va a amortizar de manera semestral. Elaborar el cuadro de
amortización correspondiente si la tasa de interés que aplica el banco es una TEA del 32%.
a) Sistema de amortización constante (método alemán)
b) Sistema de pagos única al vencimiento (método americano simple)
c) Sistema de pagos constantes (método francés)
d) Sistema de pagos con período de gracia (el banco nos concede dos períodos de gracia: el
primero parcial y el segundo total)
e) Sistema de pagos con seguro, portes y comisiones (portes y seguro $15 y $25
respectivamente)
7. Textiles Pacífico S.A.C., recibe un préstamo del BBVA por $100.000 a pagar en cinco años,
los cuales se va a amortizar de manera semestral. El banco aplica una TEA del 34%, portes
y seguros por $50 y $80 respectivamente (dichos costos no se pagan durante el período
de gracia) y una comisión por desembolsar el crédito de $2.500. Asimismo, el banco nos
concede dos años de gracia: el primer año gracia parcial, y el segundo, gracia total. Se pide:
a) Elaborar el cuadro de amortización utilizando el método francés
b) Formule el flujo de caja o flujo de efectivo del préstamo
c) Calcular el VAN considerando como tasa de descuento sólo la tasa de interés
d) Calcular la TIR del préstamo
e) Calcular el VAN considerando como tasa de descuento sólo la TIR

223. Cálculo financiero
P R O E S A D
223
REFERENCIAS BIBLIOGRÁFICAS
Aching Guzmán, César. Las Matemáticas Financieras en el Campo de los Negocios. Prociencia y
Cultura S.A. Primera Edición. Lima, 2000.
Amat, Oriol. Contabilidad y Finanzas para no Financieros. Ediciones Deusto. Empresa Editora El
Comercio S.A. Universidad Peruana de Ciencias Aplicadas (UPC). Lima, 2001.
Aliaga Valdez, Carlos. Evaluación Financiera con las funciones de Excel. Primera Edición. Lima,
1997.
Aliaga Valdez, Carlos. Manual de Matemáticas Financieras. Universidad del Pacífico. Lima, 1995.
Aliaga Valdez, Carlos. Matemáticas Financieras: Un enfoque práctico. Prentice Hall, Colombia,
2002.
Chu Rubio, Manuel. Fundamentos de Finanzas: Un enfoque peruano. Primera Edición. Lima, 2002.
Cissell, Roberth y Helen Cissell. Matemáticas Financieras. Editorial CECSA, México, 1978.
De Pablo López, Andrés, Ferruz Agudo, Luis. Finanzas de Empresa. España, 1996.
Devoto Ratto, Renzo y Mauro Núñez Abarca. Matemáticas Financieras: Un enfoque para la toma
de decisiones. Ediciones Universitarias de Valparaíso de la Universidad Católica de Valparaíso.
Santiago de Chile, 2001.
Diaz Mata. Matemática Financiera. Editorial McGraw–Hill Interamericana de España, S.A. España,
2000.
Diez de Castro, Luis y Juan Mascareñas Pérez–Iñigo. Ingeniería Financiera. Editorial McGraw–Hill
Interamericana de España, S.A. Undécima Edición. España, 1997.
García, Enrique. Matemática Financiera. Editorial McGraw–Hill Interamericana de España, S.A.
España, 2000.
Gitman, Lawrence J. Administración Financiera Básica. Editorial Harla S.A. de C.V. México, 1990.
Gonzáles Urbina, Pedro. Análisis de Estados Financieros. Universidad Peruana Unión, Facultad de
Ciencias Contables y Administrativas. Lima, 2002.
H. Moore, Justin. Manual de Matemáticas Financieras. Editorial UTHEA, México 1981.
Mascareñas, Juan. La valoración de proyectos de inversión productivos. Universidad Complutense
de Madrid. España, 2001.
Mascareñas, Juan. El Costo de Capital. Universidad Complutense de Madrid. España, 2001.
Mascareñas, Juan. Estructura de Capital Óptima. Universidad Complutense de Madrid. España,
2001.

224. U n i v e r s i d a d P e r u a n a U n i ó n
Unidad IV
224
Martín Marín, José Luis y Antonio Trujillo Ponce. Manual de valoración de empresas. Editorial
Ariel, España, 2000.
Ordiz Fuentes, Mónica y Guillermo Pérez-Bustamante Ilander. Creación de valor en la empresa
a través de las tecnologías de la información y comunicación. ESIC MARKET, España 2000.
Palomino Meneses, Oscar Hugo. Matemática Financiera. Universidad Peruana Unión, Facultad de
Ciencias Contables y Administrativas. Lima, 2002.
Portus Govinden, Lincoyán. Matemáticas Financieras. Editorial McGraw–Hill Interamericana de
España, S.A. España, 2000.
Schall, Lawrence D. y Charles W. Haley. Administración Financiera. Editorial McGraw–Hill
Interamericana de España, S.A. de C.V. México, 1988.
Terceño Gómez, Antonio. Matemática Financiera. Editorial Pirámide. España 1997.
Valera Moreno, Rafael. Matemática Financiera: Conceptos, problemas y aplicaciones. Universidad
de Piura. Lima – Perú, Tercera Edición, 2005.
Vidaurri Aguirre, Héctor Manuel. Matemáticas Financieras. Editorial Ecafsa. México, 2001.
Weston, Fred J. y Eugene F. Brigham. Fundamentos de administración financiera. Editorial
McGraw–Hill Interamericana de España, S.A. Undécima Edición. España, 1997.
Wong, David. Finanzas Corporativas: Un enfoque para el Perú. Universidad del Pacífico, Centro de
Investigación. Primera Edición. Lima, 1998.