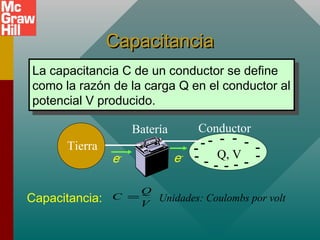
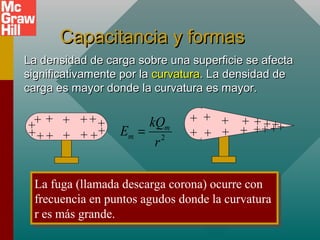
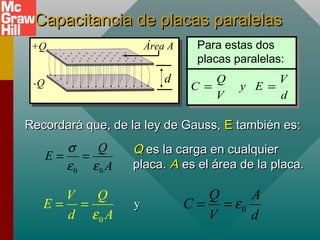
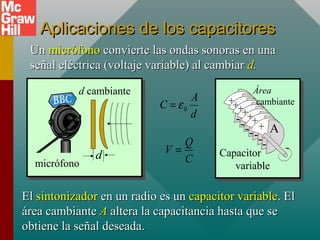
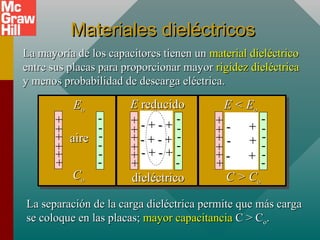
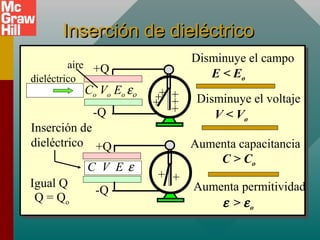
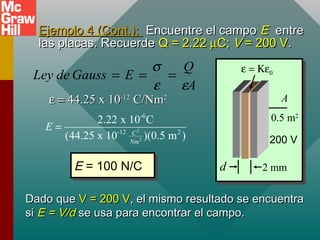
Este documento presenta un capítulo sobre capacitancia. Explica conceptos como la definición de capacitancia en términos de carga y voltaje. Describe diferentes tipos de capacitores como los de placas paralelas y esféricos, y cómo calcular su capacitancia. También cubre temas como la constante dieléctrica, la inserción de materiales dieléctricos y sus ventajas, y aplicaciones de los capacitores.

1. Capítulo 26A - Capacitancia
Capítulo 26A - Capacitancia
Presentación PowerPoint de
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University
Southern Polytechnic State University
© 2007

2. Objetivos:
Objetivos: Después de completar
Después de completar
este módulo deberá:
este módulo deberá:
• Definir la
Definir la capacitancia
capacitancia en términos de carga
en términos de carga
y voltaje, y calcular la capacitancia para un
y voltaje, y calcular la capacitancia para un
capacitor de placas paralelas
capacitor de placas paralelas dados la
dados la
separación y el área de las placas.
separación y el área de las placas.
• Definir la
Definir la constante dieléctrica
constante dieléctrica y aplicarla a
y aplicarla a
cálculos de voltaje, intensidad de campo
cálculos de voltaje, intensidad de campo
eléctrico y capacitancia.
eléctrico y capacitancia.
• Encontrar la
Encontrar la energía potencial
energía potencial almacenada
almacenada
en capacitores.
en capacitores.

3. Máxima carga sobre un
Máxima carga sobre un
conductor
conductor
Tierra
Batería Conductor
- - - - -
-
-
--
- - - - -
e-
e-
Una
Una batería
batería establece una diferencia de potencial que
establece una diferencia de potencial que
puede bombear electrones
puede bombear electrones e
e-
-
de una
de una tierra
tierra (Tierra) a un
(Tierra) a un
conductor
conductor
Existe un límite a la cantidad de carga que un
conductor puede retener sin fuga al aire. Existe
cierta capacidad para retener carga.
Existe un límite a la cantidad de carga que un
conductor puede retener sin fuga al aire. Existe
cierta capacidad para retener carga.

4. Capacitancia
Capacitancia
La capacitancia C de un conductor se define
como la razón de la carga Q en el conductor al
potencial V producido.
La capacitancia C de un conductor se define
como la razón de la carga Q en el conductor al
potencial V producido.
Tierra
Batería Conductor
- - - - -
-
-
--
- - - - -
e-
e-
Capacitancia:
Q, V
Unidades: Coulombs por volt
V
Q
C =

5. Capacitancia en farads
Capacitancia en farads
Un
Un farad (F)
farad (F) es la capacitancia
es la capacitancia C
C de un conductor que
de un conductor que
retiene un coulomb de carga por cada volt de potencial.
retiene un coulomb de carga por cada volt de potencial.
(C)
; (F)
(V)
Q coulomb
C farad
V volt
= =
Ejemplo:
Ejemplo: Cuando 40
Cuando 40 µ
µC de carga se colocan en un
C de carga se colocan en un
conductor, el potencial es 8 V. ¿Cuál es la
conductor, el potencial es 8 V. ¿Cuál es la
capacitancia?
capacitancia?
40 C
8 V
Q
C
V
µ
= = C = 5 µF
C = 5 µF

6. Capacitancia de conductor esféric
Capacitancia de conductor esférico
+Q
r
E y V en la superficie.
En la superficie de la esfera:
En la superficie de la esfera:
2
;
kQ kQ
E V
r r
= =
0
1
4
k
πε
=
Recuerde:
Recuerde:
0
4
kQ Q
V
r r
πε
= =
Y:
Y: Capacitancia:
Capacitancia:
Q
C
V
=
0
4
Q Q
C
V Q r
πε
= = 0
4
C r
πε
=
Capacitancia, C

7. Ejemplo 1:
Ejemplo 1: ¿Cuál es la capacitancia de
¿Cuál es la capacitancia de
una esfera metálica de 8 cm de radio?
una esfera metálica de 8 cm de radio?
r = 0.08 m
Capacitancia, C
+Q
r
Capacitancia: C = 4
Capacitancia: C = 4πε
πεο
οr
r
2
-12 C
N m
4 (8.85 x 10 )(0.08 m)
C π ⋅
=
C = 8.90 x 10-12
F
C = 8.90 x 10-12
F
Nota: La capacitancia sólo depende de parámetros
físicos (el radio r) y no está determinada o por la carga
o por el potencial. Esto es cierto para todos los
capacitores.
Nota: La capacitancia sólo depende de parámetros
físicos (el radio r) y no está determinada o por la carga
o por el potencial. Esto es cierto para todos los
capacitores.

8. (8.90 pF)(400 V)
Q =
Q = 3.56 nC
Q = 3.56 nC
Carga total sobre el conductor:
Carga total sobre el conductor:
Ejemplo 1 (Cont.):
Ejemplo 1 (Cont.): ¿Qué carga Q se
¿Qué carga Q se
necesita para dar un potencial de 400 V?
necesita para dar un potencial de 400 V?
r = 0.08 m
Capacitancia, C
+Q
r
C = 8.90 x 10-12
F
C = 8.90 x 10-12
F
;
Q
C Q CV
V
= =
Nota: El farad (F) y el coulomb (C) son unidades
extremadamente grandes para electricidad estática. Con
frecuencia se usan los prefijos micro µ, nano n y pico p.
Nota: El farad (F) y el coulomb (C) son unidades
extremadamente grandes para electricidad estática. Con
frecuencia se usan los prefijos micro µ, nano n y pico p.

9. Rigidez dieléctrica
Rigidez dieléctrica
La
La rigidez dieléctrica
rigidez dieléctrica de un material es aquella
de un material es aquella
intensidad eléctrica
intensidad eléctrica E
Em
m para la que el material
para la que el material
se convierte en conductor. (Fuga de carga.)
se convierte en conductor. (Fuga de carga.)
r
Q
Dieléctrico
E
Em
m varía considerablemente
varía considerablemente
con condiciones físicas y
con condiciones físicas y
ambientales como presión,
ambientales como presión,
humedad y superficies.
humedad y superficies.
Para el aire: Em = 3 x 106
N/C para superficies
esféricas y tan bajo como 0.8 x 106
N/C para
puntos agudos.
Para el aire: Em = 3 x 106
N/C para superficies
esféricas y tan bajo como 0.8 x 106
N/C para
puntos agudos.

10. Ejemplo 2:
Ejemplo 2: ¿Cuál es la carga máxima que se
¿Cuál es la carga máxima que se
puede colocar en una superficie esférica de
puede colocar en una superficie esférica de
un metro de diámetro? (R = 0.50 m)
un metro de diámetro? (R = 0.50 m)
r
Q
Em = 3 x 106
N/C
Máxima Q
Aire
2
2
; m
m
E r
kQ
E Q
r k
= =
2
2
6 2
N
C
9 Nm
C
(3 x 10 )(0.50 m)
9 x 10
Q =
Carga máxima en aire:
Carga máxima en aire: Qm = 83.3 µC
Qm = 83.3 µC
Esto ilustra el gran tamaño del coulomb como
unidad en aplicaciones electrostáticas.
Esto ilustra el gran tamaño del coulomb como
unidad en aplicaciones electrostáticas.

11. Capacitancia y formas
Capacitancia y formas
La densidad de carga sobre una superficie se afecta
La densidad de carga sobre una superficie se afecta
significativamente por la
significativamente por la curvatura
curvatura. La densidad de
. La densidad de
carga es mayor donde la curvatura es mayor.
carga es mayor donde la curvatura es mayor.
+ + + +
+
++ + + +
++
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
La fuga (llamada descarga corona) ocurre con
frecuencia en puntos agudos donde la curvatura
r es más grande.
La fuga (llamada descarga corona) ocurre con
frecuencia en puntos agudos donde la curvatura
r es más grande.
2
m
m
kQ
E
r
=

12. Capacitancia de placas paralelas
Capacitancia de placas paralelas
d
Área A
+Q
-Q
Recordará que, de la ley de Gauss,
Recordará que, de la ley de Gauss, E
E también es:
también es:
0 0
Q
E
A
σ
ε ε
= = Q
Q es la carga en cualquier
es la carga en cualquier
placa.
placa. A
A es el área de la placa.
es el área de la placa.
0
V Q
E
d A
ε
= = y
y 0
Q A
C
V d
ε
= =
Para estas dos
placas paralelas:
d
V
E
y
V
Q
C =
=

13. Ejemplo 3.
Ejemplo 3. Las placas de un capacitor
Las placas de un capacitor
de placas paralelas tienen una área de
de placas paralelas tienen una área de
0.4 m
0.4 m2
2
y están separadas 3 mm en
y están separadas 3 mm en
aire. ¿Cuál es la capacitancia?
aire. ¿Cuál es la capacitancia?
3 mm
d
A
0.4 m2
0
Q A
C
V d
ε
= =
2
2
-12 2
C
Nm
(8.85 x 10 )(0.4 m )
(0.003 m)
C =
C = 1.18 nF
C = 1.18 nF

14. Aplicaciones de los capacitores
Aplicaciones de los capacitores
+
+
+
+
+
+
+
-
-
-
-
-
-- A
Capacitor
variable
Área
cambiante
0
A
C
d
ε
=
d
d cambiante
micrófono
Q
V
C
=
Un
Un micrófono
micrófono convierte las ondas sonoras en una
convierte las ondas sonoras en una
señal eléctrica (voltaje variable) al cambiar
señal eléctrica (voltaje variable) al cambiar d
d.
.
El
El sintonizador
sintonizador en un radio es un
en un radio es un capacitor variable
capacitor variable. El
. El
área cambiante
área cambiante A
A altera la capacitancia hasta que se
altera la capacitancia hasta que se
obtiene la señal deseada.
obtiene la señal deseada.

15. Materiales dieléctricos
Materiales dieléctricos
La mayoría de los capacitores tienen un
La mayoría de los capacitores tienen un material dieléctrico
material dieléctrico
entre sus placas para proporcionar mayor
entre sus placas para proporcionar mayor rigidez dieléctrica
rigidez dieléctrica
y menos probabilidad de descarga eléctrica.
y menos probabilidad de descarga eléctrica.
La separación de la carga dieléctrica permite que más carga
La separación de la carga dieléctrica permite que más carga
se coloque en las placas;
se coloque en las placas; mayor capacitancia
mayor capacitancia C > C
C > Co
o.
.
+
+
+
+
+
+
-
-
-
-
-
-
aire
aire
C
Co
o
E
Eo
o
+
+
+
+
+
+
-
-
-
-
-
-
- +
- +
- +
- +
- +
- +
C > C
C > Co
o
E < E
E < Eo
o
+
+
+
+
+
+
-
-
-
-
-
-
- + - +
- + - +
- + - +
- + - +
- + - +
- + - +
dieléctrico
dieléctrico
E
E reducido
reducido

16. • Menor separación de placas sin contacto.
Menor separación de placas sin contacto.
• Aumenta la capacitancia de un capacitor.
Aumenta la capacitancia de un capacitor.
• Se pueden usar voltajes más altos sin
Se pueden usar voltajes más altos sin
descarga disruptiva.
descarga disruptiva.
• Con frecuencia permite mayor resistencia
Con frecuencia permite mayor resistencia
mecánica.
mecánica.
• Menor separación de placas sin contacto.
Menor separación de placas sin contacto.
• Aumenta la capacitancia de un capacitor.
Aumenta la capacitancia de un capacitor.
• Se pueden usar voltajes más altos sin
Se pueden usar voltajes más altos sin
descarga disruptiva.
descarga disruptiva.
• Con frecuencia permite mayor resistencia
Con frecuencia permite mayor resistencia
mecánica.
mecánica.
Ventajas de los dieléctricos
Ventajas de los dieléctricos

17. Inserción de dieléctrico
Inserción de dieléctrico
+
+
+
+
+
+
Co Vo Eo εο
+Q
-Q
+
+
+Q
-Q
dieléctrico
aire
Aumenta permitividad
ε > εo
Aumenta capacitancia
C > Co
Disminuye el voltaje
V < Vo
Disminuye el campo
E < Eo
Inserción de
dieléctrico
Igual Q
Q = Qo
C V E ε

18. Constante dieléctrica, K
Constante dieléctrica, K
La
La constante dieléctrica K
constante dieléctrica K para un material es la
para un material es la
razón de la capacitancia
razón de la capacitancia C
C con este material a la
con este material a la
capacitancia
capacitancia C
Co
o en el vacío.
en el vacío.
Constante dieléctrica:
K = 1 para el aire
Constante dieléctrica:
K = 1 para el aire
0
C
K
C
=
K también se puede dar en términos de voltaje
K también se puede dar en términos de voltaje V
V,
,
intensidad de campo eléctrico
intensidad de campo eléctrico E
E o permitividad
o permitividad ε
ε:
:
0 0
0
V E
K
V E
ε
ε
= = =

19. La permitividad de un medio
La permitividad de un medio
La capacitancia de un capacitor de placas
La capacitancia de un capacitor de placas
paralelas con un dieléctrico se puede encontrar de:
paralelas con un dieléctrico se puede encontrar de:
0 0
or or
A A
C KC C K C
d d
ε ε
= = =
La constante
La constante ε
ε es la
es la permitividad
permitividad del medio que
del medio que
relaciona la densidad de las líneas de campo.
relaciona la densidad de las líneas de campo.
2
2
-12 C
0 0 Nm
; 8.85 x 10
K
ε ε ε
= =

20. Ejemplo 4:
Ejemplo 4: Encuentre la capacitancia
Encuentre la capacitancia C
C y la
y la
carga
carga Q
Q si se conecta a una batería de
si se conecta a una batería de 200-V
200-V.
.
Suponga que la constante dieléctrica es
Suponga que la constante dieléctrica es K = 5.0
K = 5.0.
.
2 mm
d
A
0.5 m2
ε = Κε0
ε = Κε0= 5(8.85 x 10-12
C/Nm2
)
ε
εο
ο =
= 44.25 x 10
44.25 x 10-12
-12
C/Nm
C/Nm2
2
2
2
-12 2
C
Nm
(44.25 x 10 )(0.5 m )
0.002 m
A
C
d
ε
= =
C = 11.1 nF
C = 11.1 nF
¿Q si se conecta a V = 200 V?
¿Q si se conecta a V = 200 V?
Q = CV = (11.1 nF)(200 V)
Q = CV = (11.1 nF)(200 V) Q = 2.22 µC
Q = 2.22 µC

21. Ejemplo 4 (Cont.):
Ejemplo 4 (Cont.): Encuentre el campo
Encuentre el campo E
E entre
entre
las placas. Recuerde
las placas. Recuerde Q = 2.22
Q = 2.22 µ
µC;
C; V
V = 200 V
= 200 V.
.
ε =
ε = 44.25 x 10
44.25 x 10-12
-12
C/Nm
C/Nm2
2
2
2
-6
-12 2
2.22 x 10 C
(44.25 x 10 )(0.5 m )
C
Nm
E =
E = 100 N/C
E = 100 N/C
Dado que
Dado que V = 200 V
V = 200 V, el mismo resultado se encuentra
, el mismo resultado se encuentra
si
si E = V/d
E = V/d se usa para encontrar el campo.
se usa para encontrar el campo.
2 mm
d
A
0.5 m2
ε = Κε0
200 V
A
Q
E
Gauss
de
Ley
ε
ε
σ
=
=
=

22. Ejemplo 5:
Ejemplo 5: Un capacitor tiene una capacitancia de
Un capacitor tiene una capacitancia de
6
6µ
µF
F con aire como dieléctrico. Una batería carga
con aire como dieléctrico. Una batería carga
el capacitor a
el capacitor a 400 V
400 V y luego se desconecta. ¿Cuál
y luego se desconecta. ¿Cuál
es el nuevo voltaje si se inserta una hoja de of
es el nuevo voltaje si se inserta una hoja de of
mica (
mica (K = 5
K = 5)? ¿Cuál es la nueva capacitancia
)? ¿Cuál es la nueva capacitancia C
C ?
?
0 0
0
;
V V
C
K V
C V K
= = =
400 V
;
5
V = V = 80.0 V
V = 80.0 V
C = Kc
C = Kco
o =
= 5(6
5(6 µ
µF)
F)
C = 30 µF
C = 30 µF
V
Vo
o = 400 V
= 400 V
Mica, K = 5
Dieléctrico aire
Dieléctrico aire
Dieléctrico mica
Dieléctrico mica

23. Ejemplo 5 (Cont.):
Ejemplo 5 (Cont.): Si la batería de
Si la batería de 400 V
400 V se
se
reconecta después de insertar la mica, ¿qué
reconecta después de insertar la mica, ¿qué
carga
carga adicional
adicional se agregará a las placas
se agregará a las placas
debido a la
debido a la C
C aumentada?
aumentada?
Q
Q0
0 = C
= C0
0V
V0
0 =
= (6
(6 µ
µF)(400 V)
F)(400 V)
∆Q = 9.60 mC
∆Q = 9.60 mC
V
Vo
o = 400 V
= 400 V
Mica, K = 5
Aire C
Aire Co
o = 6
= 6 µF
Mica C = 30
Mica C = 30 µF
Q
Q0
0 = 2400
= 2400 µ
µC
C
Q = CV =
Q = CV = (30
(30 µ
µF)(400 V)
F)(400 V)
Q = 12,000
Q = 12,000 µ
µC
C
∆
∆Q = 12,000
Q = 12,000 µ
µC – 2400
C – 2400 µ
µC
C
∆
∆Q =
Q = 9600
9600 µ
µC
C

24. Energía de capacitor cargado
Energía de capacitor cargado
La
La energía potencial U
energía potencial U de un capacitor
de un capacitor
cargado es igual al trabajo (
cargado es igual al trabajo (qV
qV) que se
) que se
requiere para cargar el capacitor.
requiere para cargar el capacitor.
Si se considera que la diferencia de
Si se considera que la diferencia de
potencial promedio de 0 a V
potencial promedio de 0 a Vf
f es
es V/2
V/2:
:
Trabajo = Q(V/2) = ½QV
Trabajo = Q(V/2) = ½QV
2
2
1 1
2 2
; ;
2
Q
U QV U CV U
C
= = =

25. Ejemplo 6:
Ejemplo 6: En el Ej. 4 se encontró que la
En el Ej. 4 se encontró que la
capacitancia era be
capacitancia era be 11.1 nF
11.1 nF, el voltaje
, el voltaje 200 V
200 V y la
y la
carga
carga 2.22
2.22 µ
µC
C. Encuentre la energía potencial
. Encuentre la energía potencial
U
U.
.
2
1
2 (11.1 nF)(200 V)
U =
U = 222 µJ
U = 222 µJ
2
1
2
U CV
=
Verifique su respuesta con
Verifique su respuesta con
las otras fórmulas para E.P.
las otras fórmulas para E.P.
2
1
2 ;
2
Q
U QV U
C
= =
C = 11.1 nF
200 V
Q = 2.22 µC
U = ¿?
Capacitor
Capacitor
del ejemplo
del ejemplo
5
5.
.

26. Densidad de energía para capacitor
Densidad de energía para capacitor
La
La densidad de energía u
densidad de energía u es la energía por unidad de
es la energía por unidad de
volumen (
volumen (J/m
J/m3
3
). Para un capacitor de área
). Para un capacitor de área A
A y
y
separación
separación d
d, la densidad de energía
, la densidad de energía u
u se encuentra del
se encuentra del
modo siguiente:
modo siguiente:
Densidad de
Densidad de
energía
energía u
u para un
para un
campo E:
campo E:
A
A d
d .
U U
u
Vol Ad
= =
2 2
0
1 1
2 2 ( )
A
U CV Ed
d
ε
 
= =  
 
2
1
0
2 AdE
U
u
Ad Ad
ε
= =
Densidad de energía u:
2
1
0
2
u E
ε
=
:
y
Recuerde 0
Ed
V
d
A
C =
=
ε

27. Resumen de fórmulas
Resumen de fórmulas
(C)
; (F)
(V)
Q coulomb
C farad
V volt
= =
0
4
C r
πε
=
0
Q A
C K
V d
ε
= =
0 0
0 0
V E
C
K
C V E
ε
ε
= = = =
2
2
1 1
2 2
; ;
2
Q
U QV U CV U
C
= = =
2
1
0
2
u E
ε
=

28. CONCLUSIÓN: Capítulo 25
CONCLUSIÓN: Capítulo 25
Capacitancia
Capacitancia