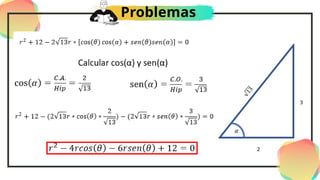
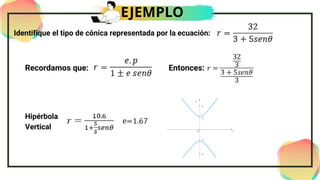
El documento presenta información sobre ecuaciones polares de cónicas. Explica las coordenadas polares, define las cónicas (circunferencia, parábola, elipse, hipérbola) y presenta sus ecuaciones polares. También incluye ejemplos de aplicación de las leyes de Kepler sobre órbitas planetarias y satelitales.

1. Equipo 1
Ecuaciones polares de las
canonicas

2. Integrantes
• Israel Gutiérrez Herrera
• Fragoso Salinas Diego Rafael
• Ventura Garduño Brayan
• Medina Vergara Jesús
• Soto Villantes Diana Beatriz
• Paredes Perez Cristopher Alan

3. Índice
• Coordenadas Polares
• Circunferencia
• Parábola
• Elipses
• Hipérbolas

4. Coordenadas polares Coordenadas Rectangulares
(x,y)
INTRODUCCION
(r,0)

5. Forma recomendada para graficar coordenadas polares
VENTURA GARDUÑO
BRAYAN
1 Se crea un origen
2 Se extiende un eje polar
3 Se crean rayos de 30°

6. Una canónica es un lugar geométrico de un punto que se mueve en el
plano que se mueve de tal manera que la razón de la distancia desde un
punto fijo (foco) a un punto P y a por una recta fija (directriz) es
constante
La razón constante es la EXCENTRICIDAD de la canónica y se denota "e"
Definición de una
canónica
MAYOR QUE “>”
MENOR QUE”<“

7. Cuando se presente la
función “COS” podemos
afirmar que es una cónica
horizontal
TODA ECUACION POLAR DE LA CONICA OBEDECE A DOS FORMAS
Cuando se presente la
función “SEN” podemos
afirmar que es una cónica
vertical

8. Ecuación polar de la Circunferencia
Fragoso Salinas Diego
Rafael
ECUACIÓN
RECTANGULAR
DE LA
CIRCUNFERENCIA

9. Consideramos las coordenadas del centro C
= (c, α) y un punto en la circunferenciaP = (r,
θ) cuyos ángulos en uno son
respectivamente α y θ
Transformar a
coordenadas polares

14. Hallar la ecuación polar de la circunferencia
Problemas

15. Problemas

16. Hallar la ecuación polar de la circunferencia
Problemas

17. Ecuación polar de la Hipérbola
ISRAEL GUTIÉRREZ
HERRERA
ECUACIÓN POLAR DE
LA CÓNICA

18. La grafica de una ecuación polar de la forma:
Ecuación polar de la cónica
En el caso de la hipérbola la excentricidad de la
cónica debe ser mayor a 1:

19. Identifique el tipo de cónica representada por la ecuación:
EJEMPLO
Recordamos que: Entonces:
Hipérbola
horizontal

20. Identifique el tipo de cónica representada por la ecuación:
EJEMPLO
Recordamos que: Entonces:
Hipérbola
Vertical

21. Pasar una ecuación polar de
la hipérbola a cartesiana
Utilizamos
Para obtener una ecuación cartesiana:

22. Completamos trinomio cuadrado perfecto:
Sumando y restando 4 :

23. Binomio al cuadrado
Identificación de la ecuación
Hipérbola horizontal C(-
4,0) V1(-6,0) V2(-2,0)

25. Índice
• ¿Quién es Kepler?
• 1era ley de Kepler
• 2da ley de kepler
• 3era ley de Kepler

26. •Johannes Kepler​: fue una figura clave en la
revolución científica, fue un astrónomo y
matemático alemán; conocido
fundamentalmente por sus leyes sobre el
movimiento de los planetas en su orbita
alrededor del sol.
¿Quien es Kepler?
kepler johannes

27. LA LEY DE LAS ORBITAS
Todos los planetas se desplazan alrededor del Sol
describiendo órbitas elípticas. El Sol se encuentra en uno de
los focos de la elipse.
“Entonces, Fabricius, ya tengo esto: la trayectoria más
coherente del planeta [Marte] es una elipse, a le que Durero
también le llama óvalo, o ciertamente tan cerca de una
elipse que la diferencia es insensible”.
1era Ley de Kepler

28. VELOCIDAD DE LOS
PLANETAS Y SUS
ÓRBITAS
•El radio vector que une un planeta y el Sol recorre áreas
iguales en tiempos iguales.
•También conocida como: La ley de las áreas es equivalente
a la constancia del momento angular, es decir, cuando el
planeta está más alejado del Sol (afelio) su velocidad es
menor que cuando está más cercano al Sol (perihelio).
2da Ley de kepler

29. VELOCIDAD DE LOS PLANETAS Y SUS ÓRBITAS
2da Ley de kepler

30. FORMULA
2da Ley de kepler

31. PERÍODOS Y RADIOS
ORBITALES
•El radio vector que une un planeta y el Sol recorre áreas
iguales en tiempos iguales.
Para cualquier planeta, el cuadrado de su período orbital es
directamente proporcional al cubo de la longitud del semieje
mayor de su órbita elíptica.
3era Ley de Kepler

32. FORMULA
Los cuadrados de los periodos orbitales de los planetas son proporcionales a los cubos de su
distancia promedio al Sol, es decir:
3era Ley de Kepler
Planeta (1) y Planeta (2) Planeta (1) y Planeta (2)

35. •El cometa Halley tiene una órbita elíptica, con el Sol en uno de sus focos y una excentricidad e=0.967
La longitud del eje mayor de la órbita es aproximadamente 35.88 unidades astronómicas (UA).
(Una unidad astronómica se define como la distancia media entre la Tierra y el Sol, 93 millones de
millas.)
Hallar una ecuación polar de la órbita. ¿Qué tan cerca llega a pasar el cometa Halley del Sol?
•Solución:
Utilizando un eje vertical, se puede elegir una ecuación de la forma.
Como los vértices de la elipse se encuentran en θ=π/2 y θ=3π/2 la longitud del eje mayor es la
suma de los valores r en los vértices.
Es decir:
2(a)=[0.967d/1+0.967]+[0.967/1-0.967]-> 2(a)= 35.83
Por tanto: d=1.204 y ed=(0.967)(1.204)=1.164
•R=ED/(1+E SENΘ)
Ejemplo 1era Ley de Kepler

36. •Usando este valor en la ecuación se obtiene:
r=1.164/1+0.967 senθ
•Donde r se mide en unidades astronómicas.
• Para hallar el punto más cercano al Sol (el foco), se escribe:
c=ea=(0.967)(1.164)=17.35 .
•Puesto que c es la distancia entre el foco y el centro,
el punto más cercano es:
a-c=17.94-17.35=0.59UA=55,000,000 millas
Ejemplo 1era Ley de Kepler

37. •El periodo del asteroide Apolo es de 661 días terrestres, y su orbita queda descrita aproximadamente
por la elipse:
R=1/1+(5/9)cosθ=9/9+5cosθ
Donde r se mide en unidades astronómicas. ¿Cuanto tiempo necesita Apolo para moverse de la posición dada
por: θ= -π/2 a θ= pi/2.?
•Para empezar se encuentra el área barrida cuando θ aumenta de -pi/2 a pi/2.
Solución
USANDO LA FORMULA PARA EL AREA DE UNA GRAFICA POLAR:
Usando la sustitución u= tan(θ/2) obtenemos:
Ejemplo 2da Ley de Kepler

38. •Como el eje mayor de la elipse tiene longitud 2(a)=81/28 y la excentricidad es e=5/9 s
encuentra que
•Obteniendo:
•Como el tiempo requerido para recorrer la orbita es 661 días, se puede aplicar la segunda
ley de kepler para concluir que el tiempo t requerido para moverse de la posición θ=-pi/2
a la posición θ=pi/2 esta dado por:
•t/661=área del segmento elíptico/área de la elipse=0.90429/5.46507
Lo cual implica que t=109 días
A=PI(AB)=PI(81/56)(9√56)=5.46507
Ejemplo 2da Ley de Kepler

39. La Luna orbita la Tierra con un periodo de 27.3 días, y su distancia promedio es de
hasta el centro de la Tierra. Si el radio de la Tierra es 6380km ¿Podemos calcular el período
de un satélite artificial que orbita a una altitud promedio de 1,500 m por encima de la
superficie de nuestro planea?
Ejemplo 3era Ley de Kepler
Tenemos como datos:
Y nos están pidiendo Ts = ?
Según la tercera ley de Kepler, se cumple que:

40. Reemplazando:
Resultado: El satélite tendrá un periodo de 1.93 horas a una altura de 1500 km
obre la superficie terrestre
Ejemplo 3era Ley de Kepler