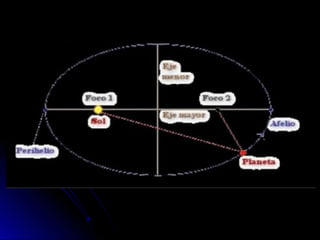
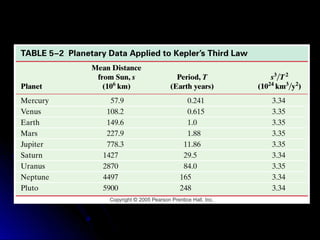
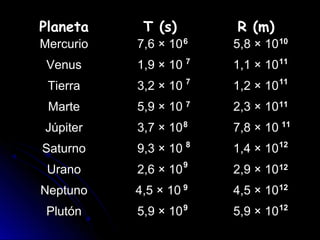
Johannes Kepler formuló tres leyes sobre el movimiento planetario basándose en las observaciones de Tycho Brahe. La primera ley establece que los planetas se mueven en órbitas elípticas con el Sol en uno de los focos. La segunda ley indica que los planetas se mueven más rápido cuando están más cerca del Sol. La tercera ley relaciona el cuadrado del periodo orbital de un planeta con el cubo de su distancia media al Sol.

1. LEYESLEYES
DEDE
KEPLERKEPLER

2. Johannes Kepler (1571 – 1630)Johannes Kepler (1571 – 1630)
Astrónomo alemán, formulo un conjunto deAstrónomo alemán, formulo un conjunto de
leyes para describir el movimientoleyes para describir el movimiento
planetarioplanetario
basándose en las observaciones ybasándose en las observaciones y
mediciones realizadasmediciones realizadas
por el astrónomopor el astrónomo
danésdanés Tycho BraheTycho Brahe

3. Formuló tres leyesFormuló tres leyes
acerca de losacerca de los
movimientos demovimientos de
los planetas alos planetas a
principios del sigloprincipios del siglo
XVIIXVII

4. Primera ley:Primera ley:
Cada planeta se mueve alrededor del Sol en
orbitas elípticas en las que el Sol ocupa uno de
los focos de la elipse.
sol
planeta

6. Segunda ley:Segunda ley:
Las áreas barridas por el radio vector que une el
centro del planeta con el centro del Sol son iguales en
lapsos iguales de tiempo; como consecuencia, cuanto
más cerca está el planeta del Sol con más rapidez se
mueve.
Área 1 Área 2
sol
d1
d2

7. La velocidad a la que se desplaza por su órbita un planeta es
variable, de forma inversa a la distancia al Sol: a mayor
distancia la velocidad orbital será menor, a distancias menores
la velocidad orbital será mayor. La velocidad es máxima en el
punto más cercano al Sol (perihelio) y mínima en su punto más
lejano (afelio).

8. Tercera ley:Tercera ley:
La relación de los cuadrados de los periodos de revolución
(T), dividida por el cubo de las distancias medias al sol (R),
es una constante, es decir: T /R se cumple para cualquier
planeta del sistema solar
1
2
sol
R2
R1
t = 0
t = T1
t = 0
t = T2
2 3

9. * Esta ley es de una categoría diferente a las otras dos. No
se refiere a un solo planeta, sino que relaciona un planeta
con cada uno de los otros
(Periodo de revolución)2
(Distancia media al sol)
3
= Constante

11. PlanetaPlaneta T (s)T (s) R (m)R (m)
MercurioMercurio 7,6 × 107,6 × 10 5,8 × 105,8 × 10
VenusVenus 1,9 × 101,9 × 10 1,1 × 101,1 × 10
TierraTierra 3,2 × 103,2 × 10 1,2 × 101,2 × 10
MarteMarte 5,9 × 105,9 × 10 2,3 × 102,3 × 10
JúpiterJúpiter 3,7 × 103,7 × 10 7,8 × 107,8 × 10
SaturnoSaturno 9,3 × 109,3 × 10 1,4 × 101,4 × 10
UranoUrano 2,6 × 102,6 × 10 2,9 × 102,9 × 10
NeptunoNeptuno 4,5 × 104,5 × 10 4,5 × 104,5 × 10
PlutónPlutón 5,9 × 105,9 × 10 5,9 × 105,9 × 10
6
7
7
7
8
8
9
9
9
10
11
11
11
11
12
12
12
12

12. Ejemplo:Ejemplo:
Calcular el valor de la constante
para el planeta Saturno, con base
en los datos de la tabla anterior
T Saturno
R Saturno
(9.3 × 10 s)
(1.4 × 10 m)
3.18 × 10 m / s
=
=
3 2
8
12
18
3
2
3
2

13. * Si la distancia media entre la Tierra y el Sol es 1,5x1011
m
y entre Marte y Sol 2,24x1011
m , ¿Cuántos días tardara
Marte en describir su orbita alrededor del Sol?’

14. Ejercicio:Ejercicio:
Calcular el valor de la constante
para el planeta Mercurio, con base
en los datos de la tabla
T Mercurio
R Mercurio
2
3
=