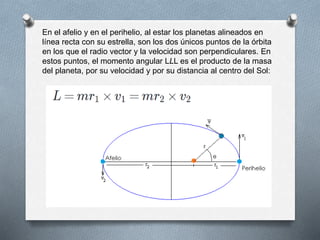
El documento describe las tres leyes de Kepler que rigen el movimiento de los planetas alrededor del sol. La primera ley establece que las órbitas son elípticas, la segunda ley se relaciona con la velocidad de los planetas y el área que recorren, y la tercera ley conecta el periodo orbital de un planeta con su distancia al sol. Además, se presentan datos sobre la excentricidad de las órbitas de diferentes planetas y las fórmulas matemáticas que respaldan estas leyes.

1. LEYES DE KEPLER
LAS TRES LEYES Y SU EXPLICACIÓN FÍSICA,
MATEMÁTICA Y GEOMÉTRICA
Samuel Darío Jordan Quimis
Universidad de Las Fuerzas Armadas- ESPE
Sede Latacunga
Ing. Diego Proaño Molina
Física Clásica 7664

2. Primera Ley de Kepler
O Denominada primera ley de las orbitas, establece
que la trayectoria existente en los planetas no es
circular, sino que tiene una forma elíptica, es decir
que se asemeja a as graficas estudiadas en
geometría, las cuales están compuestas de focos,
centros, ejes, y excentricidad.
O Figura 1 Trayectoria elíptica de un planeta alrededor del
sol (Fernandez, 2017)

3. Figura 2 Componentes de la trayectoria elíptica de un planeta con
respecto al sol (Olmo, 2016)
Es importante resaltar que la variación de distancia de un planeta con
respecto al sol tiene denominaciones, las cuales son: Cuando nos
referimos a la distancia mas larga se denomina Afelio, mientras que la
distancia mas corta entre un planeta y el sol se llama Perihelio.
La distancia que existe
cuando la tierra esta en
Perihelio con respecto al
sol es de 152 millones de
kilómetros, mientras que
cuando esta en Afelio su
distancia es de 147
millones de kilómetros.

4. Excentricidad de la órbita
O Se puede definir
como la proporción
entre la medida de
sus focos respecto al
eje mayor de la elipse
O La excentricidad está
dada por:
O 𝒆 = 𝟏 −
𝒃 𝟐
𝒂 𝟐
Excentricidad de orbitas
planetarias
Planeta Excentricidad
Mercurio 0.206
Venus 0.0068
Tierra 0.0167
Marte 0.0934
Júpiter 0.0485
Saturno 0.0556
Urano 0.0472
Neptuno 0.0086
Plutón 0.25

5. Segunda Ley de Kepler
Definición La relación que define
esta ley
O Conocida como la
ley de las áreas, en
donde se refiere a
la velocidad que se
desplaza un
planeta, esto hace
que las áreas rectas
que trazan la
distancia entre un
planeta y el sol se
recorran en el
mismo tiempo
O El tiempo que se
recorren los espacios
S1, S2, S3 serán
iguales que las Áreas 1,
2 y 3, esto se debe a lo
que explicábamos
anteriormente sobre la
fuerza de atracción
provocada por el sol.
O
𝑨 𝟏
𝒕 𝟏
=
𝑨 𝟐
𝒕 𝟐
= 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕𝒆

6. En el afelio y en el perihelio, al estar los planetas alineados en
línea recta con su estrella, son los dos únicos puntos de la órbita
en los que el radio vector y la velocidad son perpendiculares. En
estos puntos, el momento angular LLL es el producto de la masa
del planeta, por su velocidad y por su distancia al centro del Sol:

7. +
Figura 4 Distancia entre un planeta y el sol, trazada en forma
de áreas con tiempos iguales (Fernandez, 2017)
Por esta razón manifestamos que la velocidad será
directamente proporcional a la fuerza de atracción.
𝑭 ∝ 𝑽

8. Es el área que se traza por el vector de posición mientras este avanza
con el tiempo, de forma que esta velocidad es constante durante ese
breve periodo de tiempo en que tarde en recorrer toda el área.
De forma que tenemos la siguiente relación.
𝒓 𝟏 ∙ 𝒗 𝟏 ∙ 𝐬𝐢𝐧 𝜽 = 𝒓 𝟐 ∙ 𝒗 𝟐 ∙ 𝐬𝐢𝐧 𝜷
Siendo r el modulo de los dos vectores posición, v el modulo de la
velocidad en las posiciones 1 y 2, y el ángulo, como aquel que se
forma entre el vector posición y velocidad respecto a las posiciones ya
antes mencionadas, siendo expresado en radianes.

10. Representación Tercera Ley

11. Planeta
Tiempo
(días)
Distanci
a
(metros)
k
Tierra 365
𝟏. 𝟒𝟗
∙ 𝟏𝟎 𝟏𝟏
𝟒. 𝟎𝟑
∙ 𝟏𝟎−𝟐𝟗
Marte 684
𝟐. 𝟐𝟖
∙ 𝟏𝟎 𝟏𝟏
𝟑. 𝟗𝟓
∙ 𝟏𝟎−𝟐𝟗
Júpiter 4331
𝟕. 𝟕𝟖
∙ 𝟏𝟎 𝟏𝟏
𝟑. 𝟗𝟖
∙ 𝟏𝟎−𝟐𝟗

12. Explicación matemática
O La fuerza gravitacional crea la aceleración centrípeta necesaria para el
movimiento circular de radio a:
O recordando la expresión que relaciona la velocidad angular y el período de
revolución:
O de donde se deduce que el cuadrado del tiempo de una órbita completa o
periodo es:
O y despejando:
O donde es la constante de Kepler, T es el periodo orbital, a el semieje mayor
de la órbita, M es la masa del cuerpo central y G la Constante de gravitación
universal cuyo valor marca la intensidad de la interacción gravitatoria y el
sistema de unidades a utilizar para las otras variables de esta expresión. Esta
expresión es válida tanto para órbitas circulares como elípticas.

13. O En realidad C no es constante, pues esta última
expresión es solo una aproximación de la
expresión más general que se deduce con todo
rigor de las Leyes de Newton y que es:
O Donde M es la masa del cuerpo central y m la del
astro que gira en torno a él. Como en el Sistema
Solar la masa del Sol es muy superior a la de
cualquier planeta m<<M y la expresión simplificada
se obtiene de la más general haciendo M+m≈M

14. EJERCICIO