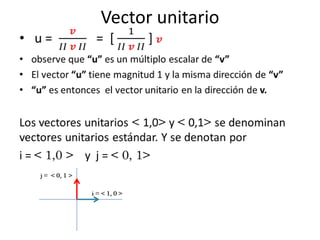
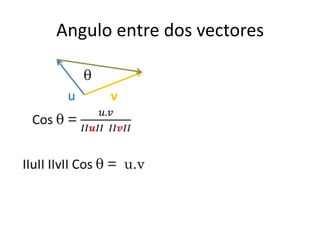
Este documento proporciona información sobre vectores y sus componentes. Explica cómo sumar, restar y multiplicar vectores, y cómo determinar el vector unitario, la magnitud y el ángulo de dirección de un vector. También cubre el producto punto de vectores, que produce un escalar, y cómo determinar si vectores son ortogonales (perpendiculares) mediante el cálculo de su producto punto. Por último, introduce conceptos como la proyección de un vector en otro y la descomposición de un vector en componentes.

1. Componentes de un vector
(posición estándar)

2. Componentes de v

4. Operaciones con vectores
D2
• Suma
NORTE
3M
D1+D2
5M
PUNTO DE
PARTIDA
4M
a=(p1, p2) y b= (q1, q2)
ESTE
D1
a + b = (p1+ q1, p2 + q2)

5. • Resta de vectores
u
u + (-v)
v
u – v = u + (-v)
u-v

6. • Sea v= < -2,5 > y w= < 3,4 > determine los
vectores
• A) 2v
• B) w – v
• C) v + 2w
•
•
•
•
•
1) u + v
2) u – v
c) 2u – 3v
a) u= < 2,3 > y v= < 4,0 >
b) u= < 0,0 > y v= < 2,1 >
c) u= i + j
v= 2i – 3j
d) u= -2i + j v= -i + 2j

7. Vector unitario

9. • Determine el vector unitario en la dirección
del vector dado.
• 1) u = < 3,0 >
• 2) u = < 0, -2 >
• 3) v = < -2, 2 >
• 4) v = < 5, -12 >
• 5) v= 6i – 2j
• 6) v = i + j

10. • Determine el vector v con la magnitud dada.
Magnitud
Dirección
1) II v II = 5
u = < 3, 3 >
2) II v II = 6
u = < -3, 3 >
3) II v II = 9
u = < 2, 5 >

11. • Sea “u” el vector con punto inicial (2,5) y punto
terminal (-1, 3) . Escriba “u” como una combinación
lineal de los vectores unitarios estándar i y j.
u = < -1- 2, 3- (-5) >
-3i + 8j
REALICE:
PUNTO INICIAL
(-3,1)
(0,-2)
(-1,-5)
(-6,4)
PUNTO TERMINAL
(4,5)
(3,6)
(2,3)
(0,1)

12. Ángulos de dirección
x
u y= sen θ
θ
x = cos θ
u = < x, y > = < cos θ, sen θ> = (cos θ)i + (sen θ)j
v = ai + bj = II v II (cos θ)i + II v II (sen θ)j

13. Determine la magnitud y el ángulo de dirección
del vector v.
• V = 3(Cos 60⁰ i + Sen 60⁰j)
• V = 8(Cos 135⁰ i + Sen 135⁰j)
• V = 6i – 6j
• V = -5i + 4j

14. Producto punto de dos vectores.
Este producto produce un escalar, en lugar de un
vector.
Definición: el producto punto de
u = < u 1 , u 2 > y v = < v1 , v2 >
es u . v = u1v1 + u2v2
Este valor (escalar) puede ser positivo,
cero o negativo.

15. • Determine los siguientes producto punto.
a) < 4, 5 > . < 2, 3 >
b) < 2, -1 > . < 1,2 >
c) < 0, 3 > . < 4,-2 >
• Sea u = < -3, 1 > , v = < 2,4 > y
w = < 1, -2 >
Encuentre : a) (u.v) w
b) u.2v

16. Angulo entre dos vectores

17. • Determine el ángulo entre
u = < 4, 3 > y v= < 3, 5 >
u = < 1, 0 > y v= < 3, 2 >
u = 3i + 4j y v= 2i – 3j

18. Vectores ortogonales
• Los términos ortogonal y perpendicular
significan esencialmente lo mismo, los
vectores de intersecan en ángulo recto.
• Los vectores u y v son ortogonales, si u.v = 0
• Ejemplo: examine si u = < 2, -3 > y v= < 6, 4 >
• u . v = 2(6) + (-3)(4) = 0

19. Definición de componentes vectoriales

20. Proyección de u en v

21. Descomposición de un vector en
componentes.