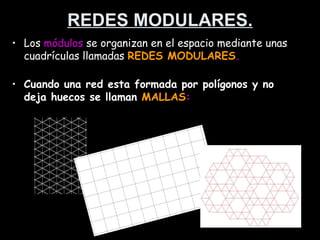
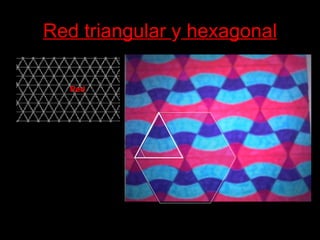
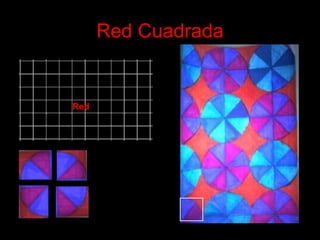
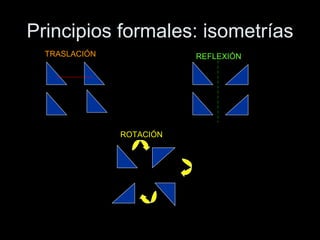
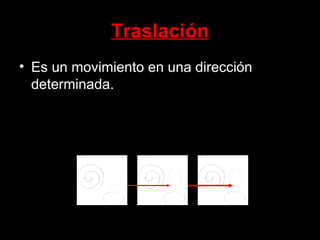
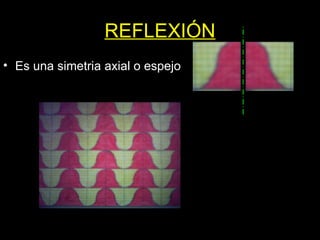
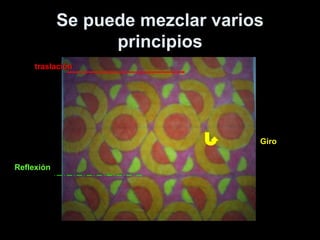
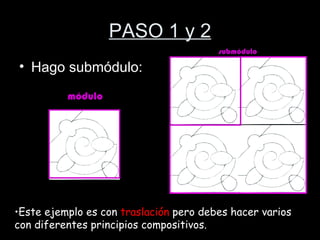
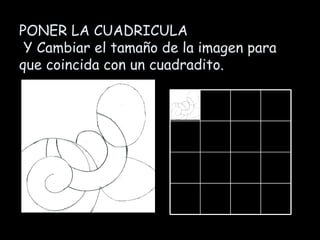
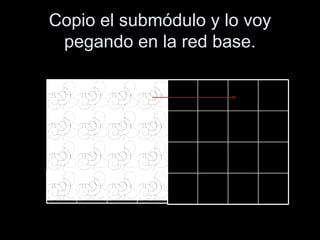
El documento habla sobre la composición modular, que es una forma de organizar elementos mediante la repetición de un módulo básico. Explica que los módulos pueden dar lugar a submódulos y que estos se organizan en redes modulares como cuadrículas o mallas. También describe los principios de isometría como traslación, rotación y reflexión que permiten repetir los módulos y crear composiciones modulares más complejas.

1. COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
MODULAR COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION
MODULAR COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICIÓN MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULARCOMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION MODULAR
MODULARCOMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION
MODULAR COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION
MODULAR COMPOSICION MODULAR COMPOSICION MODULAR COMPOSICION

2. EL MÓDULO
• Podemos componer ( organizar ) mediante el
MÓDULO:
El módulo es una forma para ser repetida y
construir una forma mayor denominada
composición modular.
Módulo
Composición

3. SUBMÓDULOS
• Varios módulos pueden dar lugar a otros
módulos.
módulo
Submódulo Composición

4. REDES MODULARES.
• Los módulos se organizan en el espacio mediante unas
cuadrículas llamadas REDES MODULARES.
MODULARES
• Cuando una red esta formada por polígonos y no
deja huecos se llaman MALLAS:
MALLAS

5. CLASES DE REDES:
SIMPLES COMPLEJAS
• Formados por • Formado por
repetición de una varias figuras
sola figura: geométricas.
• triángulos
• Cuadrados
• hexágono

6. Red triangular y hexagonal
Red

7. Red Cuadrada
Red

8. COMO REPETIR UN MÓDULO
Se utiliza los principios compositivos
– Ritmo
– Simetría axial y radial
– Formales: giro, traslación y reflexión. ( se le
llama ISOMETRIAS)

9. Principios formales: isometrías
TRASLACIÓN REFLEXIÓN
ROTACIÓN

10. Traslación
• Es un movimiento en una dirección
determinada.

11. • Cuando hacemos una composición modular
siempre hay traslación de Módulos. Hacia arriba
y hacia los lados.

12. GIROS
• Es un movimiento
que deja un solo
punto fijo, llamado
centro y lo demás gira
alrededor de el. Con
un Ángulo de giro y
un sentido:
– Podemos girar el
modulo.
– O los submódulo.

13. REFLEXIÓN
• Es una simetria axial o espejo

14. Se puede mezclar varios
principios
traslación
Giro
Reflexión

15. ¿qué vamos a hacer?

16. PASOS:
1. Tenemos una imagen de nuestro cuadro
abstracto.
2. Esa imagen va a ser el módulo.
3. Creamos submódulos mediante
isometrias.
4. Vamos a realizar diferentes
composiciones modulares.
modulares

17. PASO 1 y 2
submódulo
• Hago submódulo:
módulo
•Este ejemplo es con traslación pero debes hacer varios
con diferentes principios compositivos.

18. PONER LA CUADRICULA
Y Cambiar el tamaño de la imagen para
que coincida con un cuadradito.

19. •
Copio y pego la imagen 4 veces:
He creado el submódulo:

20. Copio el submódulo y lo voy
pegando en la red base.

21. Debe quedar asi:
• Traslacion y reflexión:
es otro ejemplo

22. Cuando tengas varias composiciones
guárdalas en el escritorio y mándalas a la
siguiente dirección:
• marazulepv@gmail.com.
• Indicando en asuntos :
epvcurso-nombre y apellidos-nombre
actividad
• Ejemplo:
Epv2ºA-MariaGarcíaGarcía-composicionmodular.