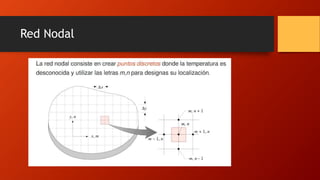
Este documento describe el método numérico de diferencias finitas para resolver problemas de conducción de calor bidimensional en estado estacionario. Explica cómo dividir la región en una malla rectangular de nodos y numerarlos para describir su posición. También describe cómo formular el balance de energía para un elemento de volumen alrededor de un nodo interior para desarrollar la ecuación aproximada por diferencias finitas, y cómo manejar los nodos frontera aplicando el mismo enfoque. Finalmente, presenta un ejemplo para ilustrar el método.

1. CONDUCCIÓN BIDIMENSIONAL
DE CALOR EN ESTADO ESTACIONARIO
Método numérico
Solanlly M.Polanco
100255155

2. CONDUCCIÓN BIDIMENSIONAL DE CALOR EN ESTADO ESTACIONARIO
• En muchos problemas necesitamos
considerar la transferencia de calor
en dos dimensiones
• •La solución de este tipo de
problemas requiere la solución de
una ecuación diferencial parcial
• Esta ecuación se puede resolver
analítica (solución exacta), gráfica o
numéricamente (soluciones
aproximadas)
• •Los métodos analíticos requieren
series y funciones matemáticamente
complicadas. –Solución exacta –
Solamente pueden resolverse cierto
tipo de problemas
• •Métodos numéricos proporcionan
resultados aproximados en puntos
discretos del volumen de control.

3. El Método de Diferencias Finitas

4. 1.En esta sección se considera la formulación numérica y la solución de la
conducción bidimensional de calor en estado estacionario en coordenadas
rectangulares,
mediante el método de diferencias finitas.
• Considere una región rectangular en la cual la conducción
de calor es significativa en las direcciones x y y. Divida
ahora el plano x-y de la región en una malla rectangular de
puntos nodales con espacios x y y en las direcciones x y y,
respectivamente, como se muestra en la figura 5-23, y
considere una profundidad unitaria de ∆z = 1 en la
dirección z.
• El objetivo es determinar las temperaturas en los nodos y
resulta conveniente numerarlos y describir su posición por
los números, en lugar de las coordenadas reales. Un
esquema lógico de numeración para los problemas
bidimensionales es la notación de subíndice doble (m, n),
donde m = 0, 1, 2, . . . , M es el conteo de los nodos en la
dirección x, y n = 0, 1, 2, . . . , N es el conteo de los
mismos en la dirección y. Las coordenadas del nodo (m, n)
son simplemente x = m∆x y y = n∆y, y la temperatura en el
nodo (m, n) se denota por Tm, n.

5. Conduction de Calor Bidimensional
• Considere ahora un elemento de
volumen de tamaño x y 1, con centro
en un nodo interior general (m, n), en
una región en la que el calor se genera
con una razón de e· y la conductividad
térmica k es constante, como se
muestra en la figura 5-24. Una vez
más, si se supone que la dirección de
laconducción de calor es hacia el nodo
que se está considerando, en todas las
superficies, el balance de energía sobre
el elemento de volumen se puede
expresar
como

6. Red Nodal

7. 2. Procedimiento

8. • Para el caso estacionario. De nuevo, si se supone que las
temperaturas entre los nodos adyacentes varían linealmente y se
nota que el área de transferencia de calor es Ax = ∆y x1 = ∆y, en
la dirección x, y Ay = ∆x x 1 = ∆x, en la dirección y, la relación de
balance de energía antes dada queda

9. APROXIMACION POR DIFERENCIAS FINITAS

10. Nodos frontera
• El desarrollo de la formulación en diferencias
finitas de los nodos frontera en los problemas
bidimensionales (o tridimensionales) es
semejante al realizado en el caso unidimensional
descrito al principio. Una vez más, la región se
divide entre los nodos mediante la formación de
elementos de volumen alrededor de ellos y se
escribe un balance de energía para cada nodo
frontera. Como se discutió para una pared plana,
se pueden manejar varias condiciones de
frontera, excepto que los elementos de volumen
en el caso bidimensional comprenden
transferencia de calor en la dirección y así como
en la dirección x.
• Las superficies aisladas todavía se conciben
como “espejos” y se puede usar el concepto de
imagen especular con el fin de tratar los nodos
sobre fronteras aisladas como nodos interiores.

12. Ejemplo 5-3