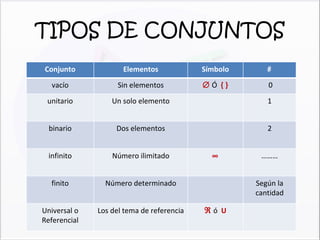
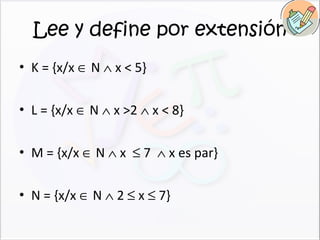El documento introduce los conceptos básicos de conjuntos matemáticos, incluyendo elementos, pertenencia, representación, determinación, tipos (vacío, unitario, binario, infinito, universal) y lenguaje simbólico. Explica cómo definir conjuntos por comprensión o enumeración, y cómo representarlos gráficamente usando diagramas de Venn.

1. CONJUNTOS Para ninguno, para uno, para muchos, para todos

2. ALGUNAS IDEAS… La palabra CONJUNTO implica la idea de una colección de objetos que se caracterizan por algo común. B: el conjunto de flores B= {x/x es una flor}

3. ELEMENTO - PERTENENCIA Los objetos que forman el conjunto se denominan ELEMENTOS. Se dice que si un elemento está dentro del conjunto, entonces PERTENECE (  )al mismo. Caso contrario, NO PERTENCE (  ) A Oso  A Cebra  A Conejo  A Tigre  A

4. Los conjuntos se designan con una letra mayúscula ( A, B, C ,…) Los conjuntos se pueden representar: entre llaves : A = { } , separando los elementos con comas mediante una curva cerrada llamada DIAGRAMA DE VENN . Nos ponemos de acuerdo A

5. DETERMINACIÓN DE UN CONJUNTO Hay dos formas de determinar conjuntos. Por extensión o enumeración : se enumeran los elementos sin repetirlos. B = {girasol, rosa, tulipán, margarita azul} Por comprensión : se indica la propiedad común. B = {x/x es una flor} Se lee: Conjunto B formado por los elementos x tales que x es una flor. B

6. Ejemplo resuelto Por comprensión: L = {x/x es una letra de la palabra “librerías”} Por extensión: L = {a, b, e, i, l, r, s} Representación:  a  b  e  i  l  r  s A

7. Expresa correctamente el conjunto de útiles de tu cartuchera Llámalo B Defínelo por comprensión. Defínelo por enumeración o extensión. Represéntalo en un diagrama de Venn. Completa con  o  Lápiz … B Botón … B Goma … B Regla … B Tiza … B Moneda … B Clip … B Tenedor … B Caramelo … B

8. Relaciona según corresponda A = {x/x es una vocal} B = {a, e, i, o, u } C = { x/x es una nota musical} D = {do, re, mi, fa, sol, la, si} E = { lunes, martes, miércoles, jueves, viernes, sábado, domingo} Por comprensión Por enumeración

9. TIPOS DE CONJUNTOS Conjunto Elementos Símbolo  vacío Sin elementos  Ó { } 0 unitario Un solo elemento 1 binario Dos elementos 2 infinito Número ilimitado  ……… finito Número determinado Según la cantidad Universal o Referencial Los del tema de referencia  ó U

10. Conjunto vacío (  ) A = {x/x es una ballena microscópica} A =  B = {x/x es un número par terminado en 3} B =  C = {x/x es el 8° día de la semana} C =  En ninguno de los casos anteriores podemos encontrar elementos pertenecientes a los conjuntos indicados.

11. Conjunto unitario ( #1 ) A = {x/x es satélite natural de la Tierra} A = {Luna] #A = 1 B = {x/x es número natural entre 3 y 5} B = {4} #B = 1 C = {x/x es vocal de la palabra “dos”} C = {o} #C = 1 En todos estos conjuntos podemos enumerar solo un elemento perteneciente al mismo.

12. Conjunto binario ( #2 ) A = {x/x es zapatilla de un par} A = {derecha, izquierda} #A = 2 B = {x/x es divisor de 3} B = {1, 3} #B = 2 C = {x/x es color neutro} C= {blanco, negro} #C = 2 En todos estos conjuntos podemos enumerar solo dos elementos pertenecientes al mismo.

13. Conjunto infinito (  ) A = {x/x es estrella del universo} A = {Sol, Alpha Centauri, Sirio, Épsilon Orionis,…} B = {x/x es múltiplo de 3} B = {3, 6, 9, 12, 15, 18, …} C = {x/x es recta del plano} C= {A, B, C, D,…} En estos conjuntos no podemos enumerar a todos los elementos pertenecientes al mismo, ya que por ser infinito, sólo se mencionan algunos.

14. Conjunto Universal ( U ) Si A = {x/x es letra de la palabra “argentina”} A = {a, e, g, i, n, r, t} Entonces U= {x/x es letra del abecedario} U = {a, b, c, d, e, …, x , y, z} El Universal o Referencial, incluye a todos los conjuntos posibles del tema de referencia.

15. Representación de U A  a  e  g  i  n  t  r U  b  c  d  f  h  j  k  l  m  ñ  o  p  q  s  u  v  w  x  y  z

16. LENGUAJE SIMBÓLICO Para nombrar conjuntos utilizamos diferentes lenguajes: Lenguaje coloquial , en el que se utilizan palabras en forma oral o escrita. Lenguaje algebraico , en el que se utilizan símbolos matemáticos.

17. ALGUNOS SÍMBOLOS  pertenece  no pertenece  está incluido  no está incluido < es menor que  es menor o igual que > es mayor que  es mayor o igual que  intersección  unión  tal que  y  ó  entonces x un elemento cualquiera N Núm. Naturales

18. EJEMPLO Coloquial: T = {número natural menor que diez} Simbólico: T = {x/x  N  x < 10} Se lee: “T es el conjunto de todos los elementos x tales que x es un número Natural menor que diez” Extensión: T = {1, 2, 3, 4, 5, 6, 7, 8, 9}

19. Lee y define por extensión K = {x/x  N  x < 5} L = {x/x  N  x >2  x < 8} M = {x/x  N  x  7  x es par} N = {x/x  N  2  x  7}

20. Define por comprensión, en forma simbólica T = {2, 4, 6, 8} W = {5, 7, 9, 11, 13} Q = {25, 50, 75} Ñ = {1; 3; 5; 15} V = {3, 4, 5, 6, 7}

21. Define, clasifica y representa los siguientes conjuntos. A = { x / x es día de la semana} B = { vocales de la palabra vals} C = { 1, 3, 5, 7, 9, . . . . .} D = { x / x es un habitante de la luna} E = { x / x  N  x < 15} F = { x / x  N  5 < x < 5 G = { x / x  N  x > 15} H = { x / x es presidente del Océano Pacífico} I = { x / x es número de cabellos total de los habitantes del Argentina}

22. FIN…. Por ahora