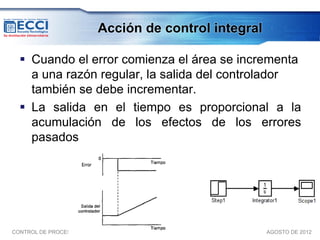
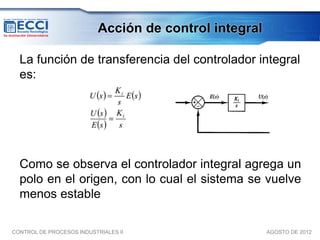
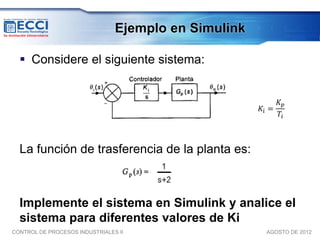
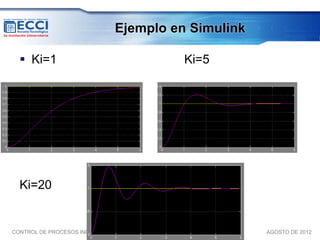
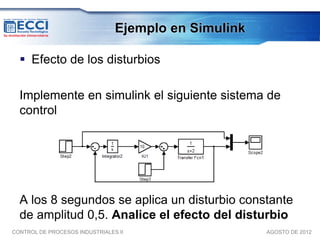
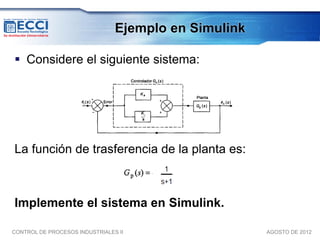
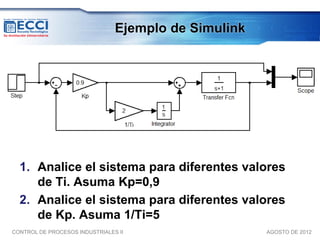
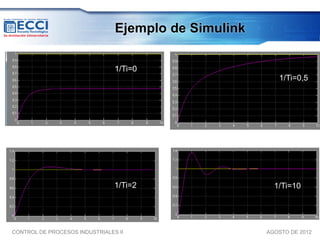
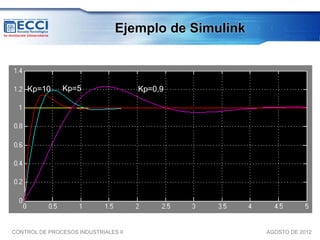
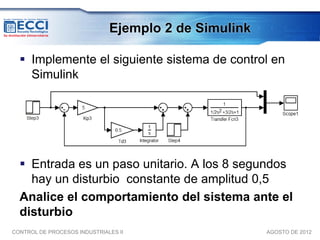
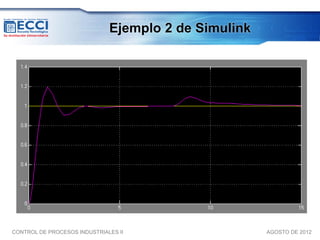
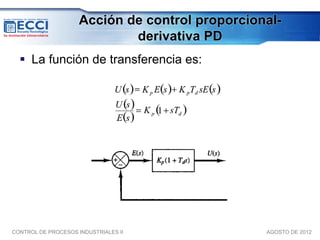
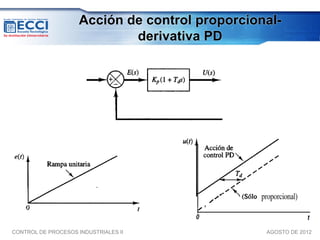
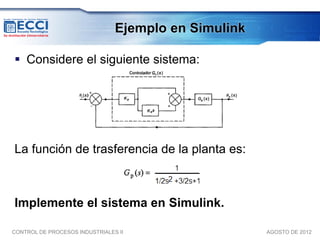
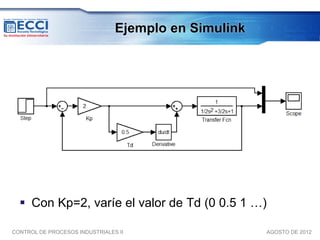
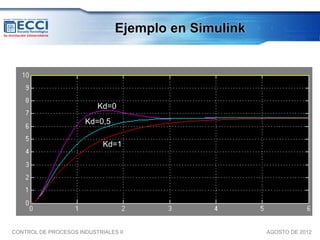
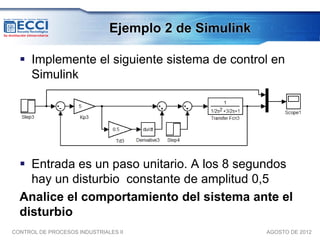
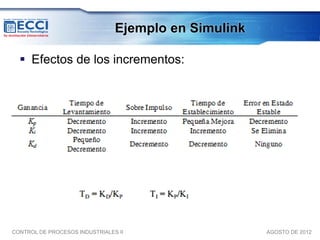
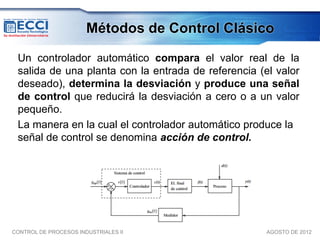
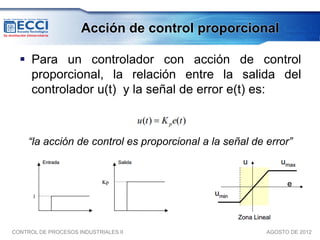
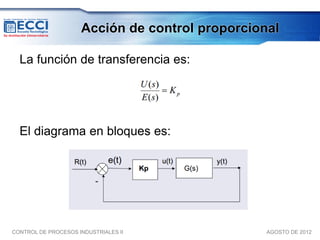
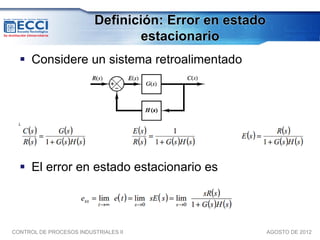
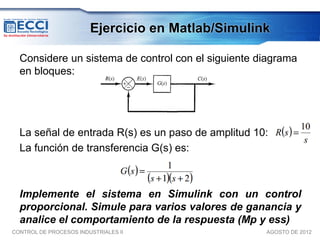
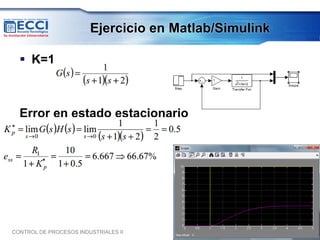
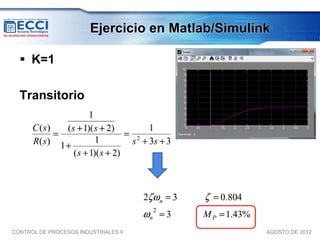
El documento trata sobre los métodos de control clásico, en particular sobre las acciones de control proporcional, integral y derivativa. Explica las ecuaciones y funciones de transferencia de cada acción, así como ejemplos de su implementación en Simulink. Finalmente, describe la acción de control PID, la cual combina las tres acciones anteriores para obtener sus ventajas.




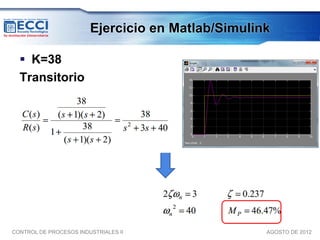


![Lugar de las raíces
num=[1];
den=conv([1 1 0],[1 2])
G=tf(num,den)
rlocus(G)
Root Locus
5
System: G
4
Gain: 6.63
Pole: 0.0287 + 1.47i
3 Damping: -0.0195
Overshoot (%): 106
2 Frequency (rad/s): 1.47
Imaginary Axis (seconds-1)
1
0
-1
-2
-3
-4
-5
-7 -6 -5 -4 -3 -2 -1 0 1 2
-1
Real Axis (seconds )
CONTROL DE PROCESOS INDUSTRIALES II AGOSTO DE 2012](https://image.slidesharecdn.com/cpi2clase4-parte1-accionesdecontrol-120830090608-phpapp01/85/CPI2-clase-4-parte-1-Acciones-de-control-20-320.jpg)