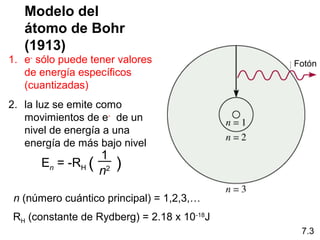
1) El documento describe las propiedades de las ondas electromagnéticas y cómo la teoría cuántica explica la estructura electrónica de los átomos. 2) Explica que la luz tiene naturaleza de onda y partícula y que los electrones solo pueden tener valores de energía específicos. 3) Detalla cómo la ecuación de Schrödinger describe la probabilidad de encontrar electrones y predice los números cuánticos que definen los orbitales atómicos.

1. Teoría cuántica y la estructura
electrónica de los átomos
Capítulo 7
Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.

2. Propiedades de las ondas
Longitud de onda (λ) es la distancia entre puntos
idénticos de ondas sucesivas.
Amplitud es la distancia vertical de la línea media a la
cresta o al vallle de la onda.
7.1
H2
Longitud de Onda
Amplitud Dirección de
propagación
de onda
Longitud de onda
Longitud de onda
Amplitud
Amplitud

3. Propiedades de las ondas
Frecuencia (ν) es el número de ondas que atraviesan un
punto particular en 1 segundo (Hz = 1 ciclo/s).
La velocidad (u) de la onda = λ x ν
7.1
Longitud de onda

4. Maxwell (1873), propusó que la luz visible consiste en
ondas electromagnéticas.
Radiación
electromagnética es la
emisión y transmisión de
energía en la forma de
ondas electromagnéticas.
La velocidad de luz (c) en el vacío = 3.00 x 108
m/s
Toda radiación electromagnética
λ x ν = c
7.1
Componente del campo eléctrico
Componente del campo magnético

5. 7.1
Rayos X Lámparas
solares
Hornos de
microondas,
radar policiaco,
estaciones de
satélite
Lámparas
incandes-
centes
TV UHF,
teléfonos
celulares
Radio FM.
TV VHF
Radio
AM
Ondas de radioMicroondasInfrarrojoUltra
violetaRayos XRayos
gamma
Tipo de radiación
Frecuencia (Hz)
Longitud
de onda (nm)

6. Misterio #1, “problema del cuerpo negro”.
Resuelto por Planck en 1900
La energía (luz) es emitida
o absorbida en unidades
discretas (cuanto).
E = h x ν
Constante de Planck (h)
h = 6.63 x 10-34
J•s
7.1

7. La luz tiene ambos:
1. naturaleza de onda
2. naturaleza de partícula
hν = KE + BE
Misterio #2, “efecto fotoeléctrico”.
Resuelto por Einstein en 1905
Fotón es una “partícula” de luz
KE = hν - BE
hν
KE e-
7.2
Luz
incidente
Fuente
de voltaje
Detector

8. 7.3
Línea del espectro de emisión de átomos de hidrógeno
Placa fotográfica
Colimador
Prisma
Espectro
de
líneas
Luz separada en
varios
componentes
Tubo de
descarga
Alto
voltaje

9. 7.3
Pectro de líneas brillantes
Metales
alcalinos
(monovalentes)
Elementos
alcalino-
térreos
(divalentes)
Metales
(divalentes)
Litio(Li)
Sodio (Na)
Potasio(K)
Calcio(Ca)
Estroncio (Sr)
Bario(Ba)
Cadmio(Cd)
Mercurio(Hg)
Hidrógeno(H)
Helio(He)
Litio(Li)

10. 1. e-
sólo puede tener valores
de energía específicos
(cuantizadas)
2. la luz se emite como
movimientos de e-
de un
nivel de energía a una
energía de más bajo nivel
Modelo del
átomo de Bohr
(1913)
En = -RH ( )
1
n2
n (número cuántico principal) = 1,2,3,…
RH (constante de Rydberg) = 2.18 x 10-18
J
7.3
Fotón

11. E = hν
E = hν
7.3

12. Efotón = ∆E = Ef - Ei
Ef = -RH ( )
1
n2
f
Ei = -RH ( )
1
n2
i
i f
∆E = RH( )
1
n2
1
n2
nf = 1
ni = 2
nf = 1
ni = 3
nf = 2
ni = 3
7.3
Series de
Brackett
Series de
Paschen
Energía

13. Efotón = 2.18 x 10-18
J x (1/25 - 1/9)
Efotón = ∆E = -1.55 x 10-19
J
λ = 6.63 x 10-34
(J•s) x 3.00 x 108
(m/s)/1.55 x 10-19
J
λ = 1280 nm
Calcule la longitud de onda (en nm) de un
fotón emitido por un átomo de hidrógeno
durante la transición de su electrón del
estado n = 5 al estado n = 3 .
Efotón = h x c / λ
λ = h x c / Efotón
i f
∆E = RH( )
1
n2
1
n2
Efotón =
7.3

14. De Broglie (1924) razonó
que el e-
es partícula y
onda.
2πr = nλ λ = h/mu
u = velocidad del e-
m = masa del e-
¿Por qué es cuantizada la
energía del e-?
7.4

15. Ecuación de la onda de Schrodinger
En 1926 Schrodinger escribió una ecuación que
describió la partícula y naturaleza de la onda del e -
La función de la onda (Ψ) describe:
1. la energía del e-
con un Ψ dado
2. la probabilidad de encontrar el e-
en un volumen
del espacio
La ecuación de Schrodinger sólo se puede resolver
exactamente para el átomo de hidrógeno. Debe
aproximar su solución para los sistemas del multi-
electrón.
7.5

16. Ecuación de la onda de Schrodinger
Ψ = fn(n, l, ml, ms)
número cuántico principal n
n = 1, 2, 3, 4, ….
n=1 n=2 n=3
7.6
distancia del e-
de los núcleos

17. la densidad del e-
(orbital 1s)
cae rápidamente al aumentar la
distancia del núcleo
Donde 90% de
la densidad
e-
se encuentra
por el orbital 1s
7.6
Distancia del
núcleo
Densidaddelelectrón

18. Ψ = fn(n, l, ml, ms)
número cuántico del momento angular l
para un valor dado de n, l = 0, 1, 2, 3, … n-1
n = 1, l = 0
n = 2, l = 0 o 1
n = 3, l = 0, 1, o 2
La forma del “volumen” de espacio que ocupa el e-
l = 0 orbital s
l = 1 orbital p
l = 2 orbital d
l = 3 orbital f
Ecuación de la onda de Schrodinger
7.6

19. l = 0 (orbitales s)
l = 1 (orbitales p)
7.6

20. l = 2 (orbitales d)
7.6

21. Ψ = fn(n, l, ml, ms)
número cuántico magnético ml
para un valor dado de l
ml = -l, …., 0, …. +l
Orientación del orbital en el espacio
if l = 1 (orbital p ), ml = -1, 0, o 1
if l = 2 (orbital d ), ml = -2, -1, 0, 1, o 2
Ecuación de la onda de Schrodinger
7.6

22. ml = -1 ml = 0 ml = 1
ml = -2 ml = -1 ml = 0 ml = 1 ml = 2
7.6

23. Ψ = fn(n, l, ml, ms)
número cuántico del spin ms
ms = +½ o -½
Ecuación de la onda de Schrodinger
ms = -½ms = +½
7.6
HornoRayo
de
átomos
Pantalla colimadora
Imán
Pantalla
detectora

24. La existencia (y energía) del electrón en el átomo se
describe por su única función de onda Ψ.
Principio de exclusión de Pauli: dos electrones en un
átomo no pueden tener los mismos cuatro números
cuánticos.
Ecuación de la onda de Schrodinger
Ψ = fn(n, l, ml, ms)
Cada lugar se identifica singularmente (E,
R12, S8)
Cada lugar puede admitir sólo uno individual
en un momento
7.6

25. Ecuación de la onda de Schrodinger
Ψ = fn(n, l, ml, ms)
Nivel(capa): electrones con el mismo valor de n
Subnivel(subcapa): electrones con los mismos valores de
n y l
Orbital: electrones con los mismos valores de n, l, y ml
¿Cuántos electrones puede admitir un orbital?
Si n, l, y ml son fijos, entonces, ms = ½ o - ½
Ψ = (n, l, ml, ½) o Ψ = (n, l, ml, -½)
Un orbital puede admitir dos electrones 7.6

26. ¿Cuántos orbitales 2p están ahí en un átomo?
2p
n=2
l = 1
Si l = 1, entonces ml = -1, 0, o +1
3 orbitales
¿Cuántos electrones pueden colocarse en el
subnivel 3d?
3d
n=3
l = 2
Si l = 2, entonces ml = -2, -1, 0, +1, o +2
5 orbitales que pueden admitir un total de 10 e-
7.6

27. Energía de orbitales en un átomo de un sólo electrón
La energía sólo depende del número cuántico principal n
En = -RH ( )
1
n2
n=1
n=2
n=3
7.7
Energía

28. La energía de orbitales en un átomo polielectrónico
La energía depende de n y l
n=1 l = 0
n=2 l = 0
n=2 l = 1
n=3 l = 0
n=3 l = 1
n=3 l = 2
7.7
Energía

29. “Llenar” electrones en orbitales de energía más baja
(Principio de Aufbau)
H 1 electrón
H 1s1
He 2 electrones
He 1s2
Li 3 electrones
Li 1s2
2s1
Be 4 electrones
Be 1s2
2s2
B 5 electrones
B 1s2
2s2
2p1
C 6 electrones
? ?
7.7
Energía

30. C 6 electrones
La distribución de electrones más
estable en los subniveles es la que
tiene el mayor número de espines
paralelos (regla de Hund).
C 1s2
2s2
2p2
N 7 electrones
N 1s2
2s2
2p3
O 8 electrones
O 1s2
2s2
2p4
F 9 electrones
F 1s2
2s2
2p5
Ne 10 electrones
Ne 1s2
2s2
2p6
7.7
Energía

31. El orden de (llenando) de orbitales en un átomo polielectrónico
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s
7.7

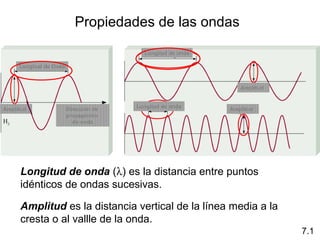
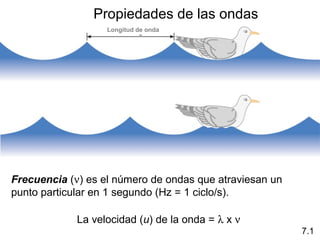
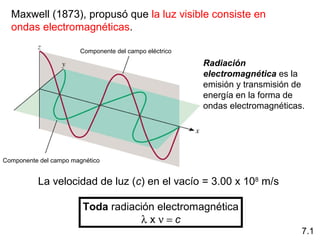
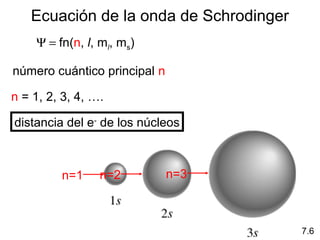
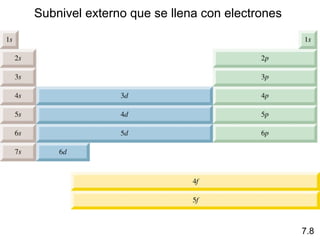
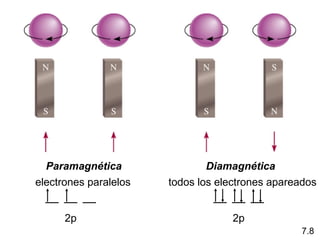
32. ¿Cuál es la configuración electrónica del Mg?
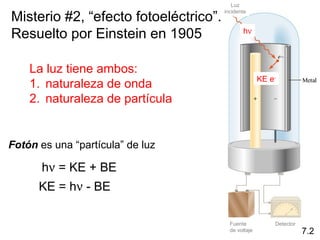
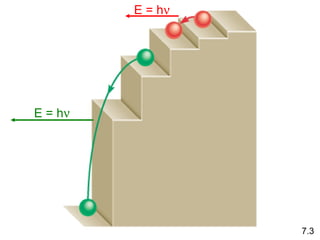
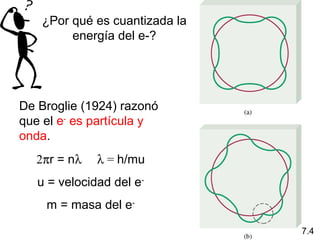
Mg 12 electrones
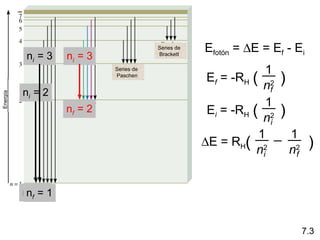
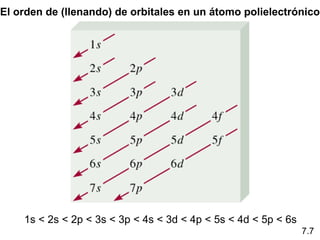
1s < 2s < 2p < 3s < 3p < 4s
1s2
2s2
2p6
3s2
2 + 2 + 6 + 2 = 12 electrones
7.7
Abreviado como [Ne]3s2
[Ne] 1s2
2s2
2p6
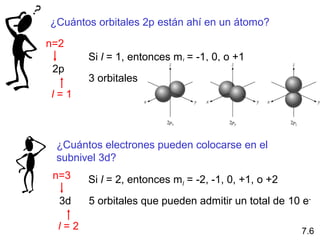
¿Cuáles son los números cuánticos posibles
para el último (externo) electrón en Cl?
Cl 17 electrones 1s < 2s < 2p < 3s < 3p < 4s
1s2
2s2
2p6
3s2
3p5
2 + 2 + 6 + 2 + 5 = 17 electrones
En último electrón sumado al orbital 3p
n = 3 l = 1 ml = -1, 0, o +1 ms = ½ o -½

33. Subnivel externo que se llena con electrones
7.8

34. Paramagnética
electrones paralelos
2p
Diamagnética
todos los electrones apareados
2p
7.8