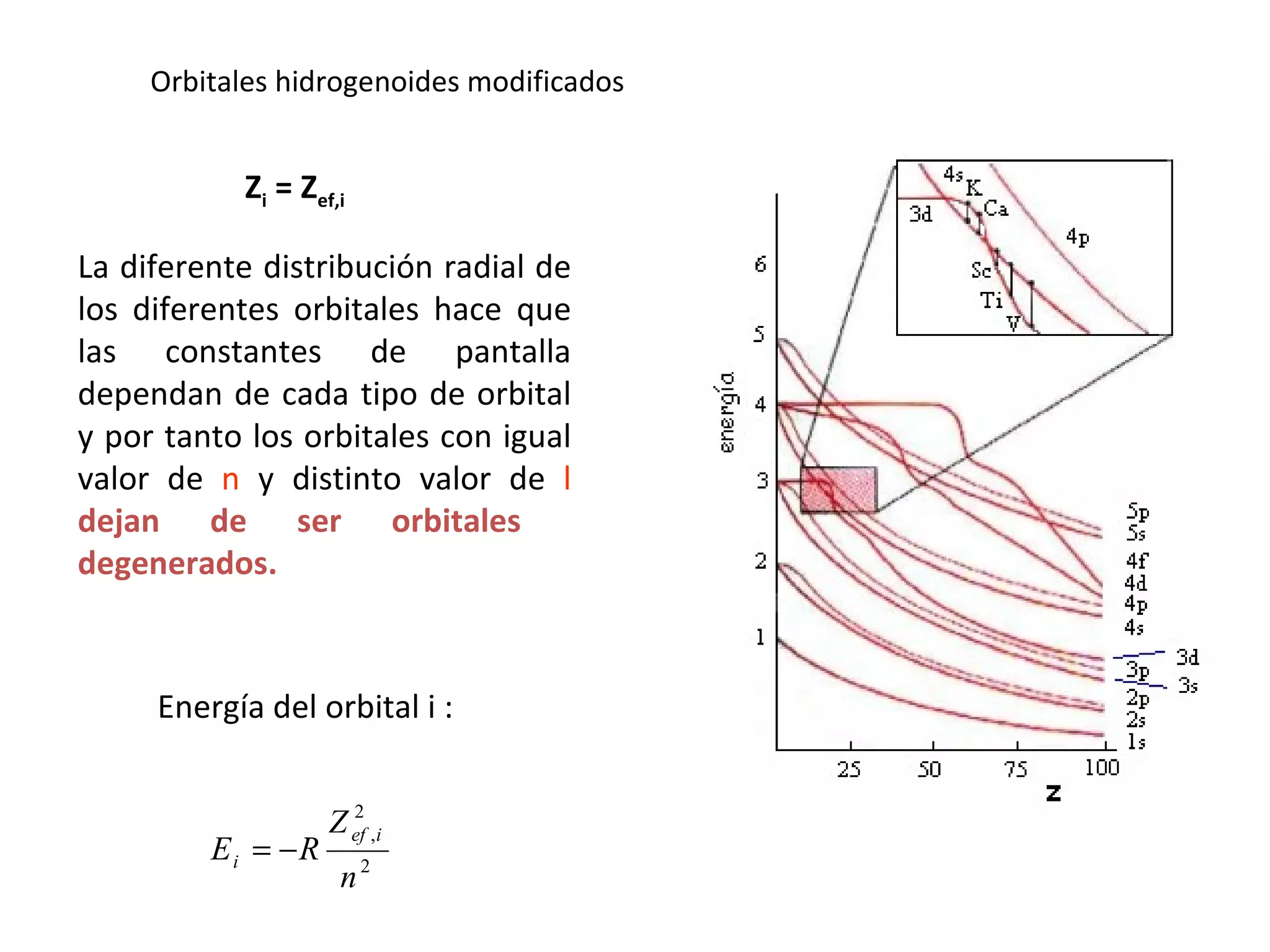
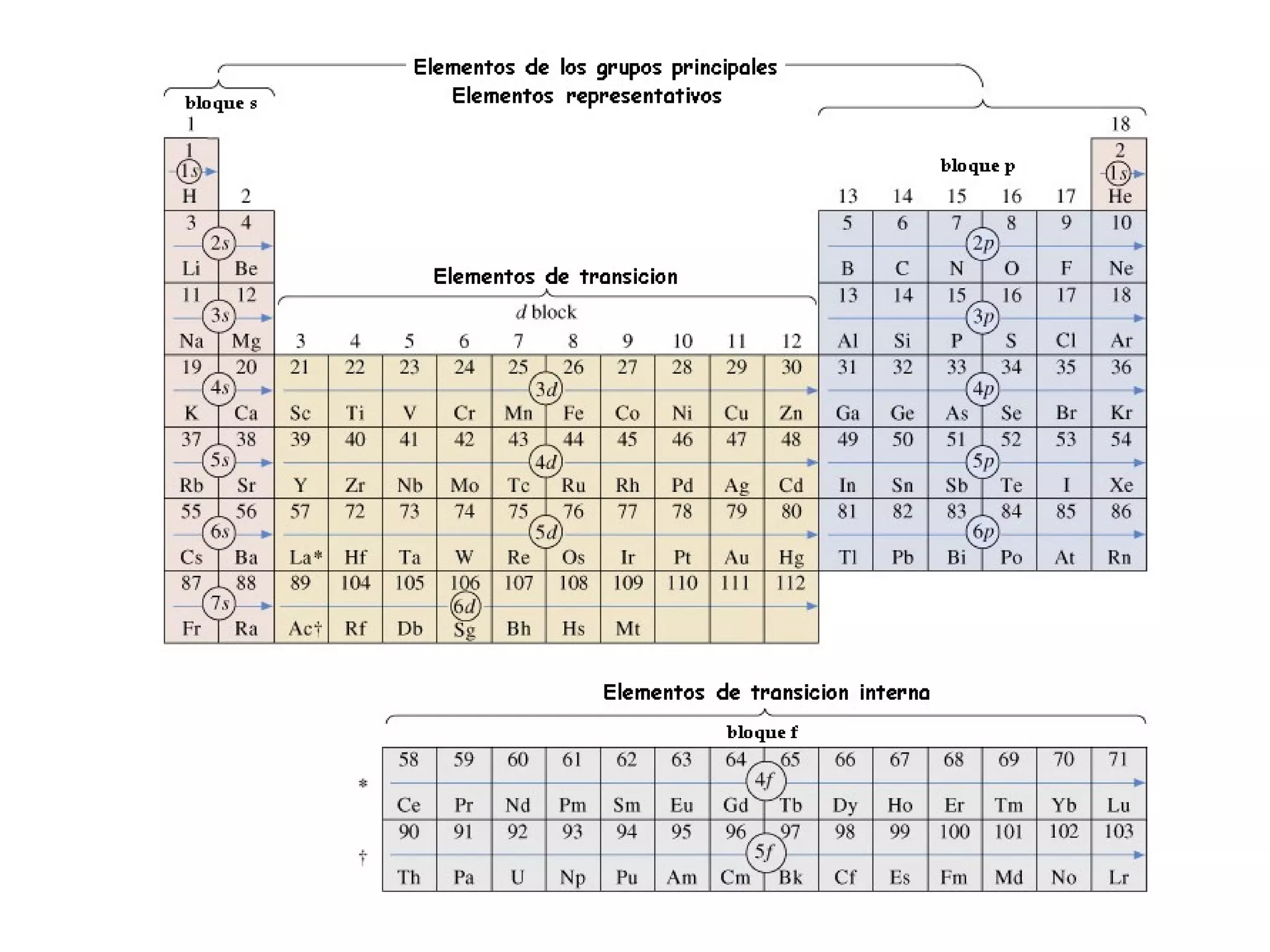
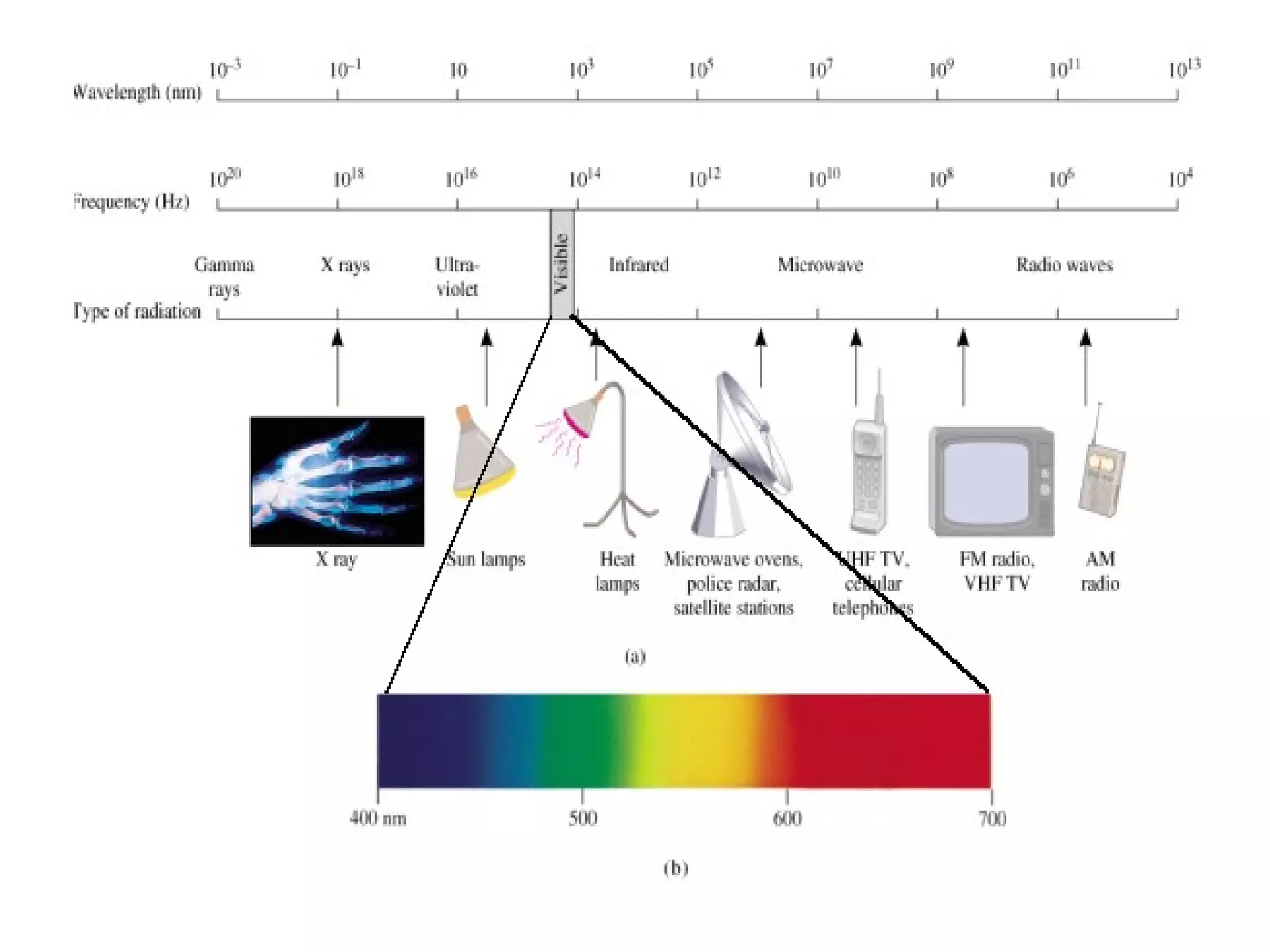
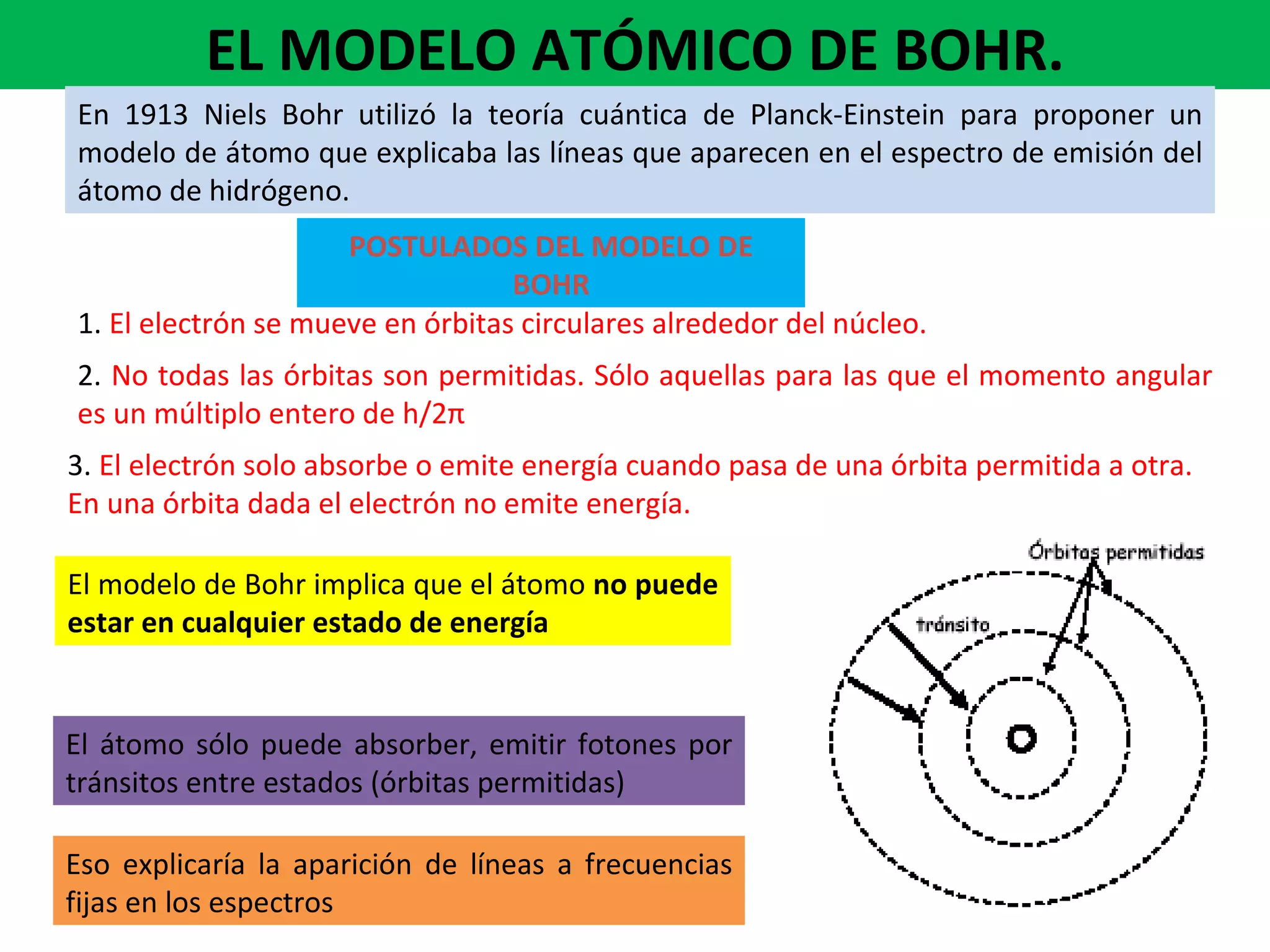
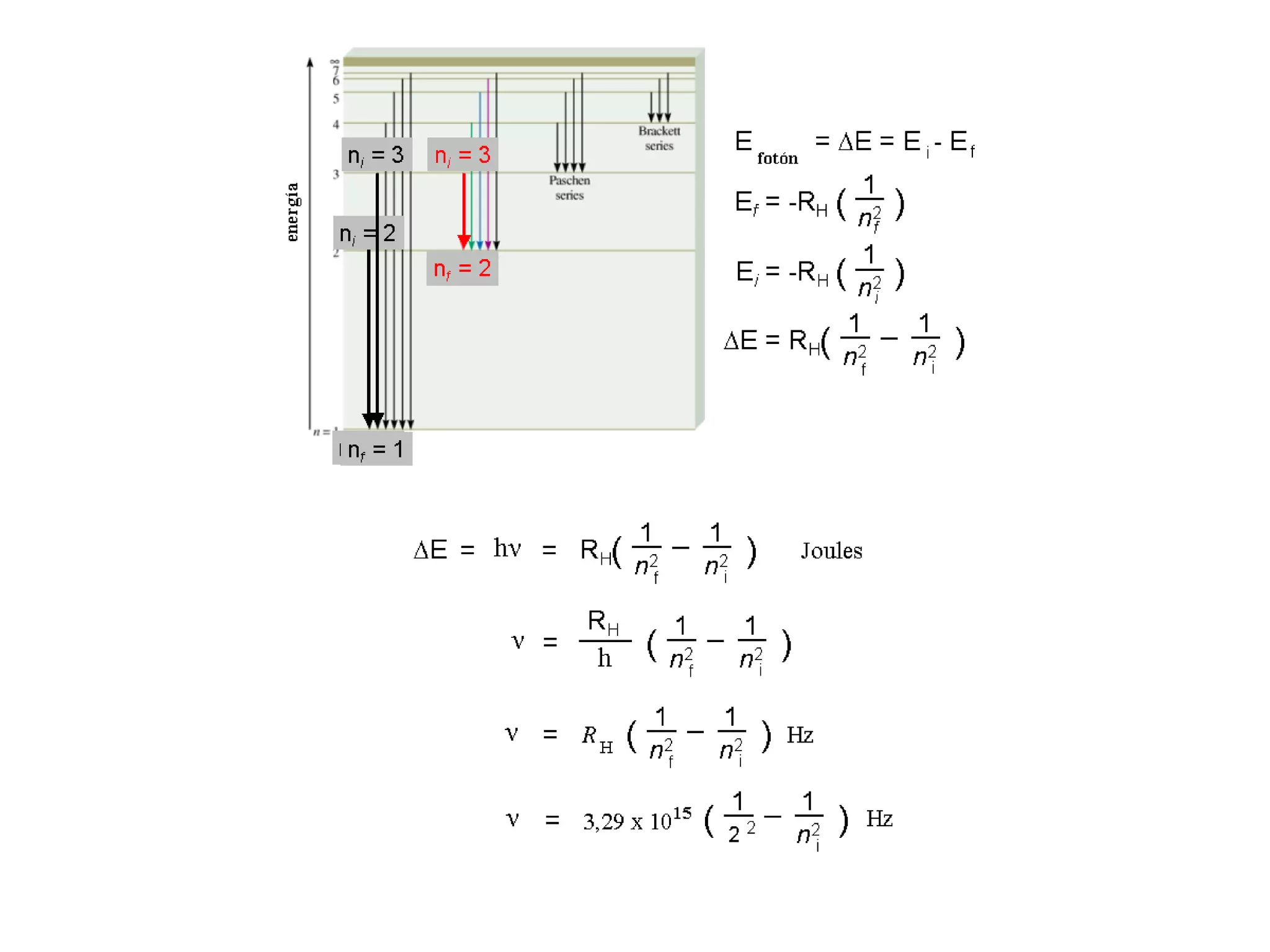
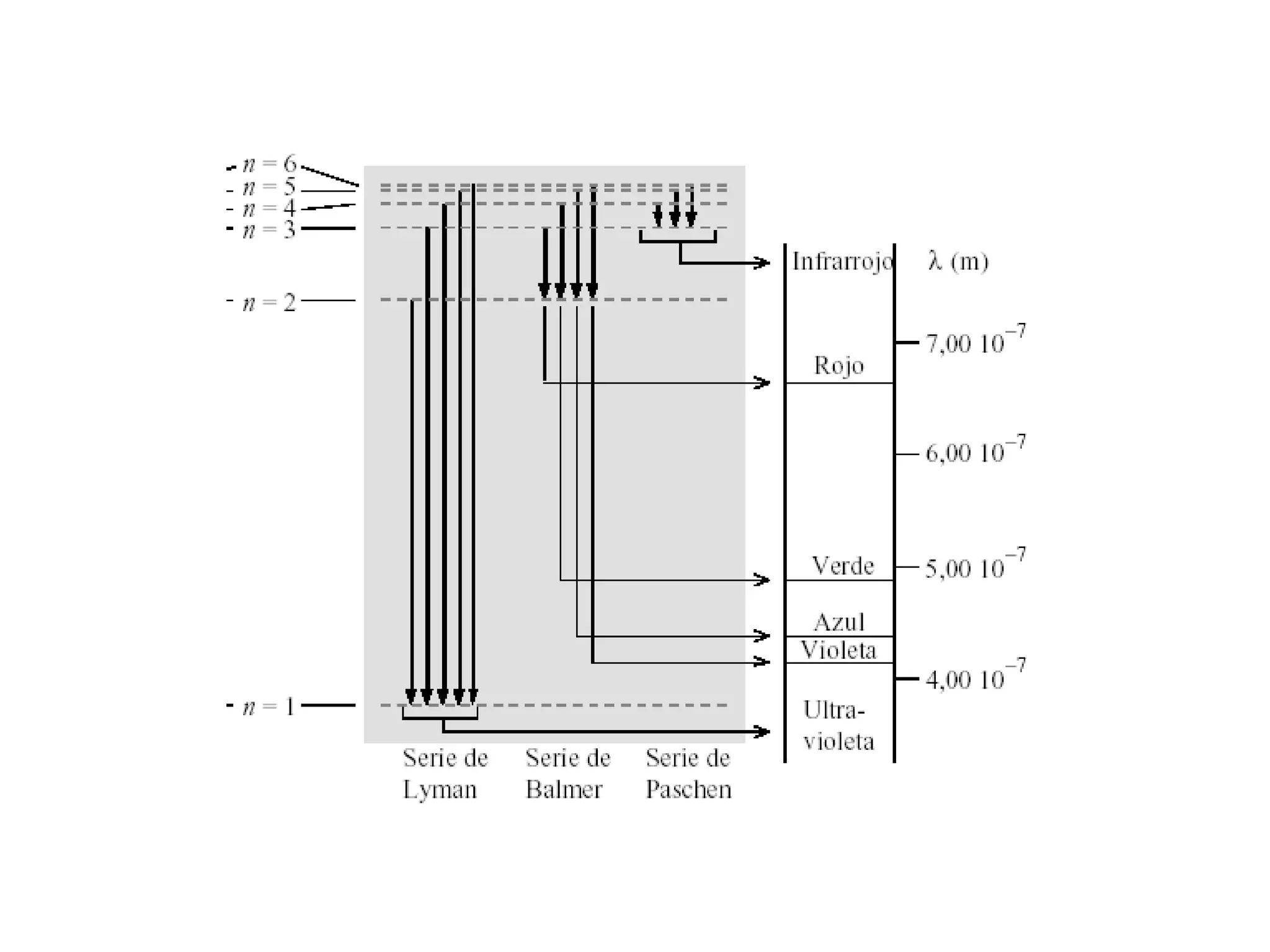
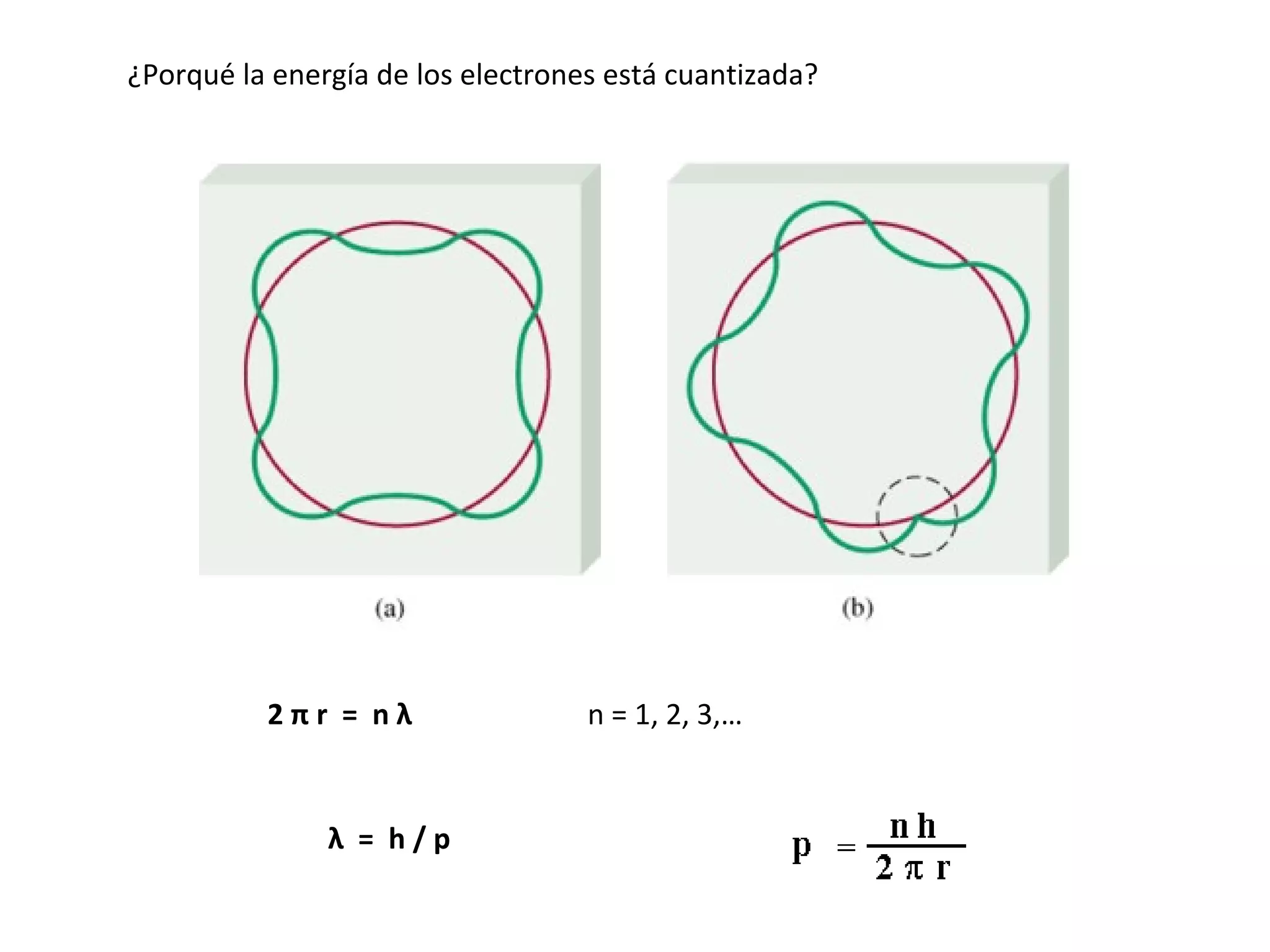
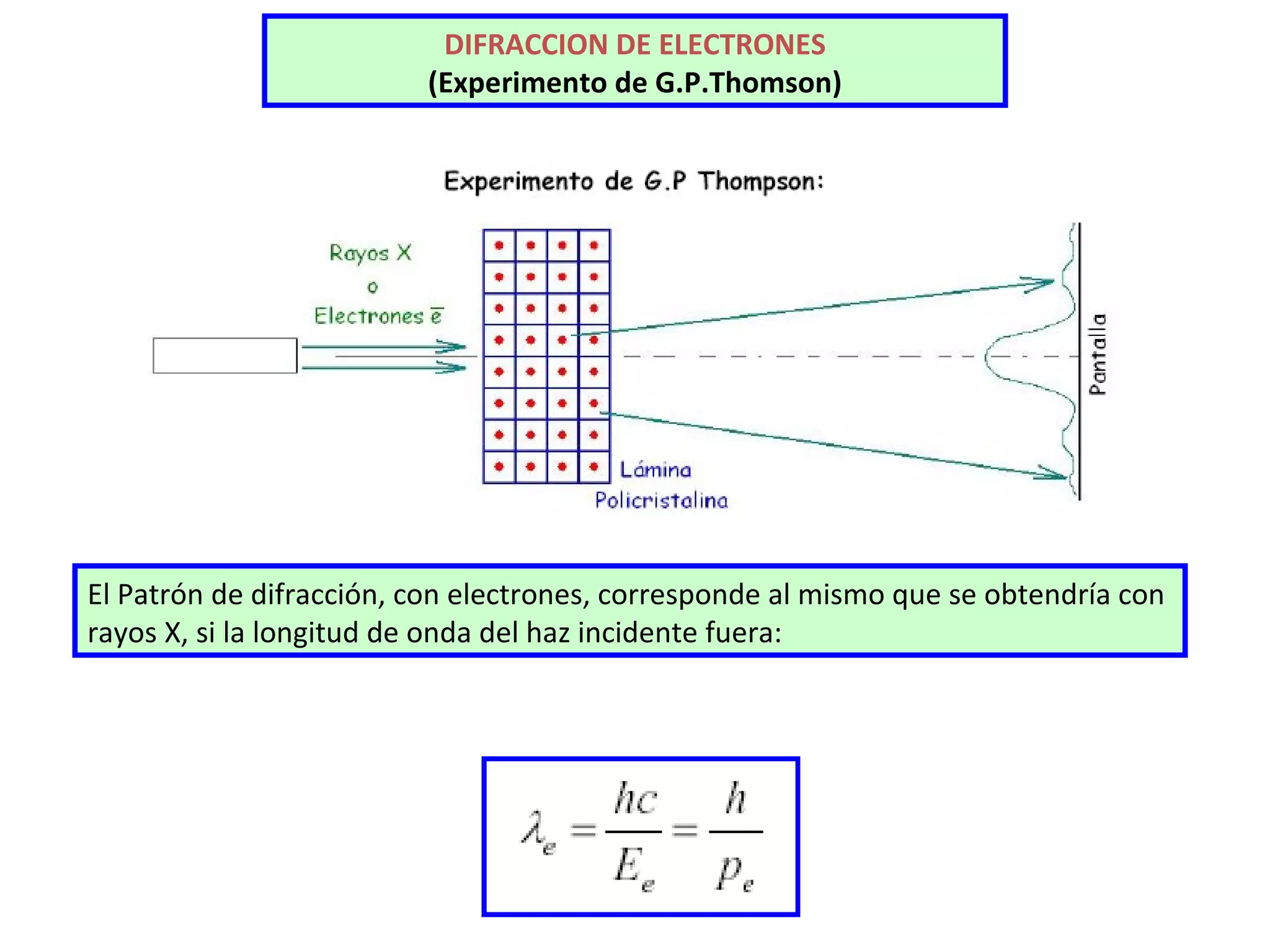
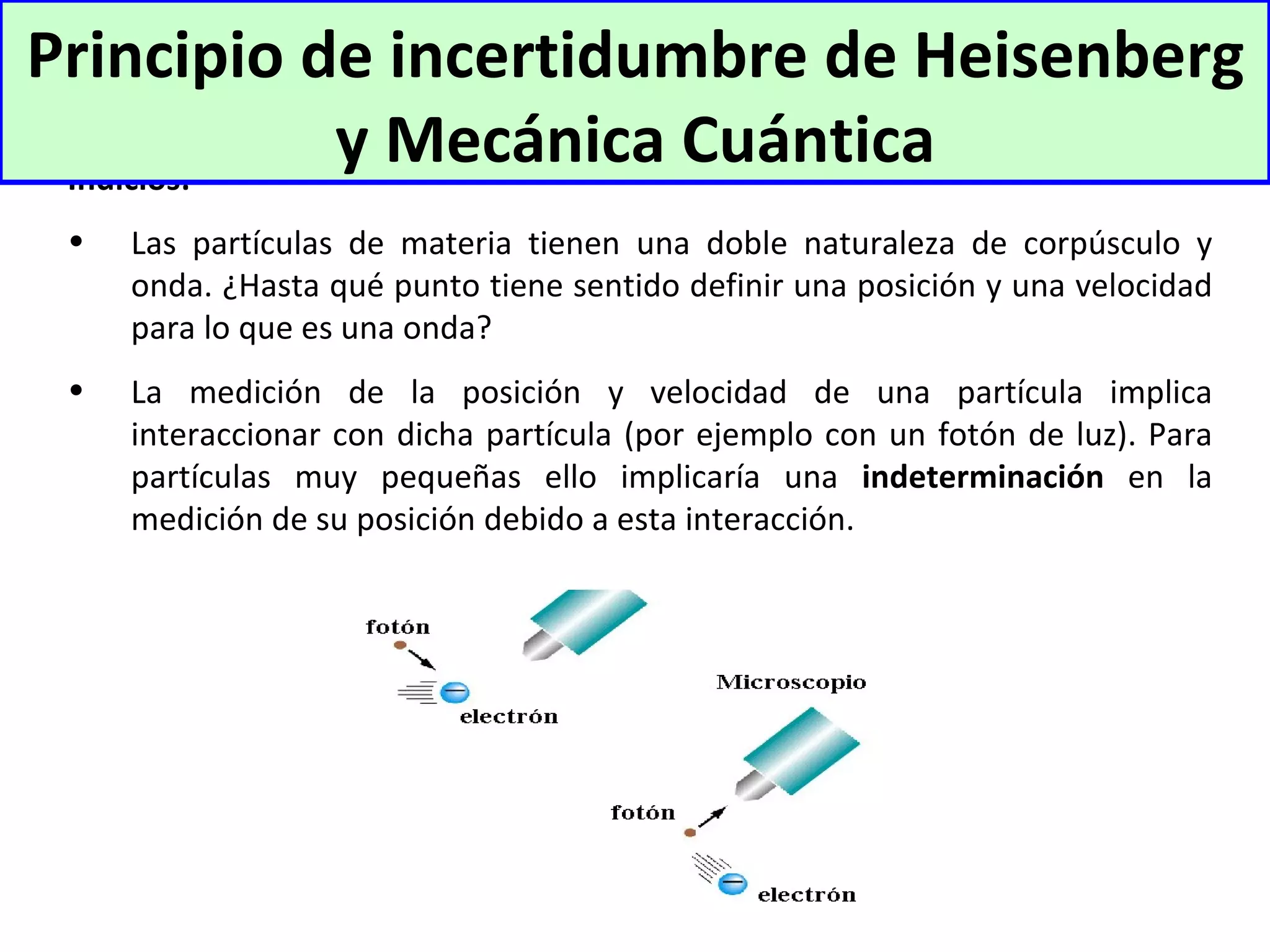
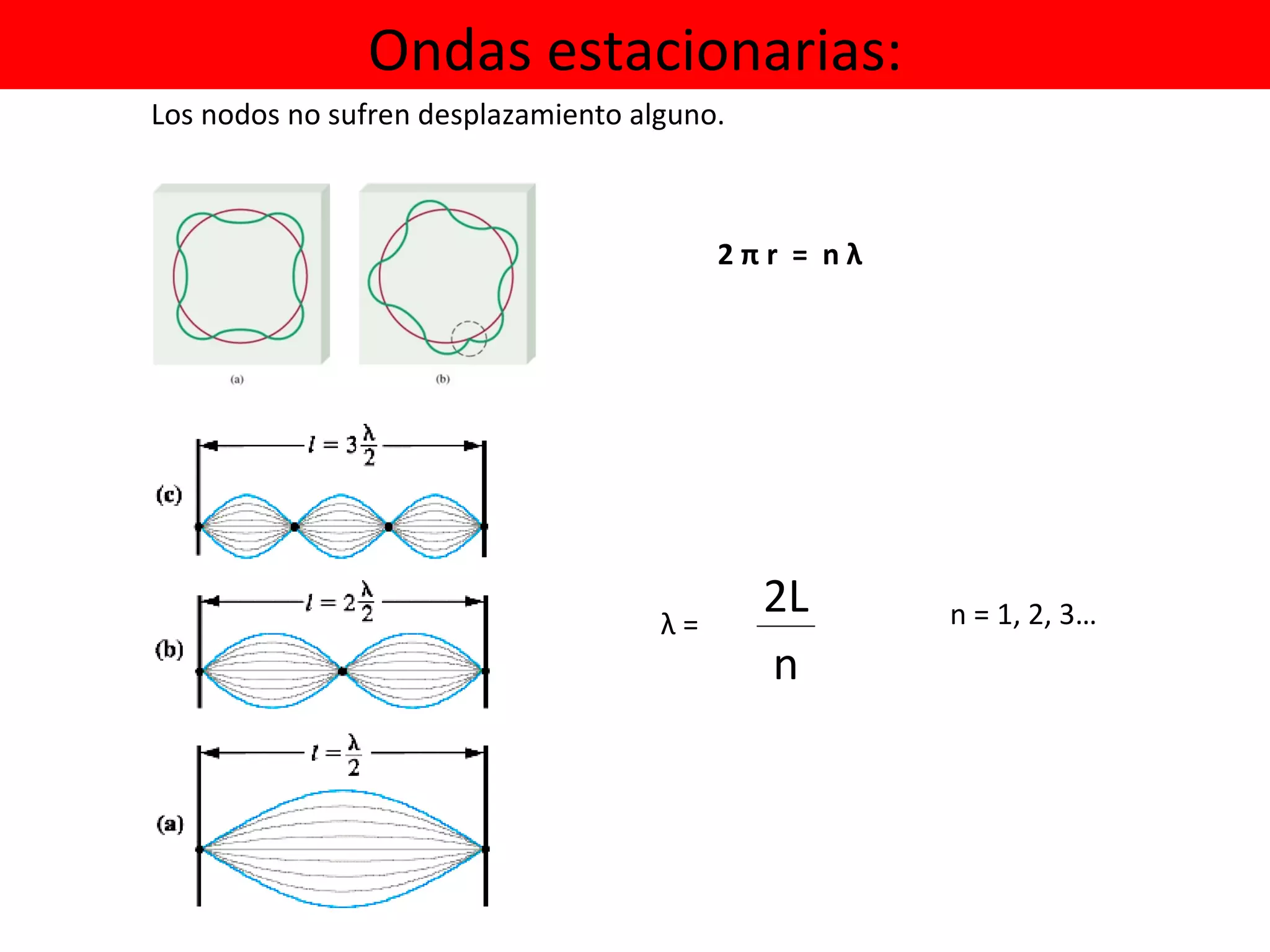
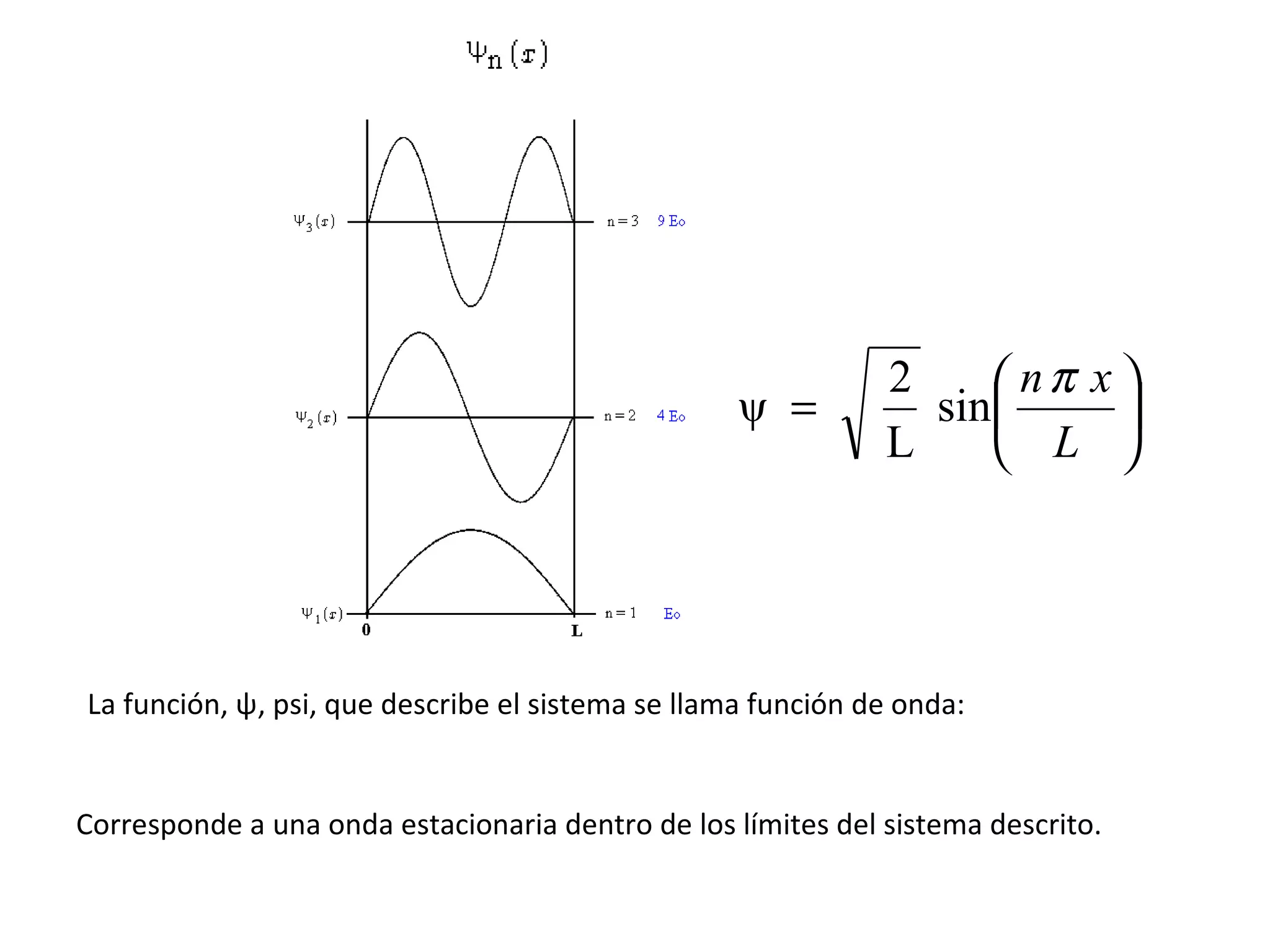
El documento describe los conceptos fundamentales de la teoría cuántica y la estructura electrónica de los átomos, incluyendo la naturaleza dual onda-partícula de la luz y los electrones, los modelos atómicos de Rutherford y Bohr, los números cuánticos y orbitales electrónicos, y cómo estos conceptos explican las líneas espectrales atómicas y la tabla periódica.

1. TEORÍA CUÁNTICA Y LA ESTRUCTURA ELECTRÓNICA DE LOS ÁTOMOS PROFESOR: EDUARDO JAIME VANEGAS LONDOÑO

2. Naturaleza de la luz y radiación electromagnética. Espectros atómicos. El electrón. Modelos atómicos. El átomo nuclear. El átomo de Bohr. Dos ideas que condujeron a la mecánica cuántica. Mecánica ondulatoria. Números cuánticos y orbitales de los electrones. Interpretación y representación de los orbitales del átomo de hidrógeno. Espín del electrón. Átomos multielectrónicos. Configuraciones electrónicas. Configuraciones electrónicas y tabla periódica.

3. Maxwell (1873), estableció que la luz está formada por ondas electromagnéticas Emisión y transmisión de energía por medio de ondas electromagnéticas. Velocidad de la luz (en el vacío) = 3.00 x 10 8 m/s Toda radiación electromagnética   c RADIACIÓN ELECTROMAGNÉTICA

4. Longitud de onda (  ) es la distancia que existe entre dos puntos equivalentes en una serie de ondas. Amplitud: Distancia vertical desde el punto medio de la curva hasta una cresta (punto máximo) o un valle (punto mínimo). PROPIEDADES DE LAS ONDAS Frecuencia (  ) es el número de ondas que pasan por un determinado punto por unidad de tiempo. (Hertz = 1 ciclo/seg).

6. ANTECEDENTES QUE LLEVARON AL DESARROLLO DE LA TEOR Í A MODERNA DE LA ESTRUCTURA AT Ó MICA • Los espectros discontinuos de los elementos A finales del siglo XIX, una serie de evidencias experimentales no podían ser explicados con las teorías clásicas (Maxwell, Newton): • La radiación del “cuerpo negro” • El efecto fotoeléctrico

7. Misterio #1 , “Problema del cuerpo negro” Resuelto por Planck en el año 1900 La energía y la luz son emitidas o absorbidas en múltiples unidades llamadas “cuantos”. E = h  Constante de Plank (h) h = 6.63 x 10 -34 J • s

8. La luz tiene: Naturaleza de onda Naturaleza de partícula Misterio #2 , “Efecto fotoeléctrico” Resuelto por Einstein en 1905 Un fotón es una “partícula” de luz h  e - KE Energía = E = h 

9. El potencial de frenado permite determinar la energía cinética de los fotoelectrones mv 2 = e V s 1 2 A frecuencias mayores de  o : V s = k (  -  o )

10. E o = h  o E c = eV s  o = eV o h eV o , y por tanto  o , son características del metal. La conservación de la energía requiere que: h  = mv 2 2 1 E fotón = E c + E unión E c = E fotón - E unión La energía cinética es cero para  o mv 2 = h  - h  o 2 1  o = Frecuencia umbral + eVo

11. LA LUZ PRESENTA DUALIDAD DE COMPORTAMIENTO ONDA – PARTICULA

12. Misterio #3: Espectros atómicos

13. Los espectros de emisión de los elementos son discontinuos, contienen líneas discretas a longitudes de onda definidas y específicas de cada elemento Espectro de emisión del hidrógeno Experimentalmente Balmer (1885) comprobó que las líneas de la serie encontrada por el en el espectro de emisión del hidrógeno aparecen a frecuencias que cumplen la ecuación: Otras series del espectro del hidrógeno y otros elementos aparecen a frecuencias que cumplen relaciones matemáticas similares (aunque más complejas) a la ecuación de Balmer . Donde n es un número entero mayor que 2 y R es la cte de Rydberg y vale 3,29 x 10 15 Hz

14. Estructura de la materia y partículas elementales Los electrones Aprox. 1850, descubrimiento de los rayos catódicos por M. Faraday Los rayos catódicos tienen propiedades que son independientes de la sustancia emisora utilizada, y responden a campos eléctricos y magnéticos como si tuvieran carga eléctrica negativa 1897, J.J. Thomson mide la relación carga/masa de las partículas que constituyen los rayos catódicos. Los denomina electrones 1906-1914, R. Millikan mide la carga del electrón

15. PRIMEROS EXPERIMENTOS SOBRE LA ESTRUCTURA ATÓMICA Tubo de rayos catódicos

19. Modelo de Rutherford (1911) A partir de los hallazgos del experimento. Casi el 100% de la masa atómica (protones y neutrones) del átomo se encuentra en el núcleo El núcleo ocupa un volumen muy pequeño comparado con el volumen ocupado por los electrones El núcleo concentra la carga positiva (protones). El conjunto del átomo es eléctricamente neutro Conclusiones:

21. Resumen de las propiedades de las partículas elementales Partículas Símbolo Carga* Masa / g electrones e- -1 9.109 × 10 -28 protones p + 1 1.673 × 10 -24 Neutrones n 0 1.673 × 10 -24 *Las cargas se dan como múltiplos de la carga del protón, que en unidades del SI es 1.6 × 10 -19 C La masa del protón corresponde a 1.0073 unidades atómicas de masa (1 u.m.a.) 1 u.m.a. = 1/12 masa de un átomo de Carbono 12

22. Número atómico y número de masa • Número Atómico, Z = número de protones en el núcleo = número de electrones en el átomo (neutralidad del átomo) Las propiedades químicas de un elemento dependen de Z • Número de masa, A = número de protones y neutrones en el núcleo Normalmente se expresa en unidades de la masa de un protón (aprox. 1 u.m.a.) Un elemento químico viene definido por su número atómico porque éste determina el número de electrones que tienen sus átomos . Número atómico y elementos químicos El número de electrones determina la estructura electrónica La estructura electrónica determina las propiedades químicas del elemento

23. EL MODELO ATÓMICO DE BOHR. En 1913 Niels Bohr utilizó la teoría cuántica de Planck-Einstein para proponer un modelo de átomo que explicaba las líneas que aparecen en el espectro de emisión del átomo de hidrógeno. POSTULADOS DEL MODELO DE BOHR El modelo de Bohr implica que el átomo no puede estar en cualquier estado de energía El átomo sólo puede absorber, emitir fotones por tránsitos entre estados (órbitas permitidas) Eso explicaría la aparición de líneas a frecuencias fijas en los espectros 1. El electrón se mueve en órbita s circular es alrededor del núcleo . 2. No todas las órbitas son permitidas. Sólo aquellas para las que el momento angular es un múltiplo entero de h/2 π 3. El electrón solo absorb e o emit e energía cuando pasa de una órbita permitida a otra. En una órbita dada el electrón no emite energía.

24. Definiendo a o (radio de Bohr) como: y definiendo la unidad at ó mica de energ í a, hartree, como:

27. Dualidad onda-corpúsculo La explicación de la emision de radiacion por un cuerpo negro y del efecto fotoeléctrico mostraba que la radiación electromagnética tiene una doble naturaleza de onda y corpúsculo ¿Tienen las partículas de materia también doble naturaleza de onda y corpúsculo? En 1924 Luis De Broglie propuso esa posibilidad Ecuación de Einstein: E = m c 2 (c velocidad de la luz )  = h / p Ecuación de Planck: E = h  Combinando ambas ecuaciones Luis De Broglie propuso que una partícula pequeña que se mueve posee asociada una onda de longitud de onda,  , igual a: en que h es la constante de Planck y p es el momento de la partícula

28. 2 π r = n λ λ = h / p ¿Porqué la energía de los electrones está cuantizada? n = 1, 2, 3,…

29. ¿Cuál es la longitud de onda de De Broglie (en nm) de una pelota de ping-pong de 2.5 gramos de masa que tiene una velocidad constante de 15.6 m/s?  = h/mv  = 6.63 x 10 -34 / (2.5 x 10 -3 x 15.6)  = 1.7 x 10 -32 m = 1.7 x 10 -23 nm m en kg h en J • s v en (m/s)

31. DIFRACCION DE ELECTRONES (Experimento de G.P.Thomson) El Patrón de difracción, con electrones, corresponde al mismo que se obtendría con rayos X, si la longitud de onda del haz incidente fuera:

32. Indicios: Las partículas de materia tienen una doble naturaleza de corpúsculo y onda. ¿Hasta qué punto tiene sentido definir una posición y una velocidad para lo que es una onda? La medición de la posición y velocidad de una partícula implica interaccionar con dicha partícula (por ejemplo con un fotón de luz). Para partículas muy pequeñas ello implicaría una i ndeterminación en la medición de su posición debido a esta interacción. Principio de incertidumbre de Heisenberg y Mecánica Cuántica

33. Heisenberg (1927): “Es imposible conocer la posición y el momento lineal de una partícula simultáneamente” Δp Δx  h/ 4 π Δp = incerteza en el momento Δx = incerteza en la posición El error en la determinación de la posición de una bala de 1g cuya velocidad se conoce con una precisión de 1 mm s -1 es de 5 · 10 -26 m . El error en la determinación de la velocidad de un electrón en un espacio unidimensional de anchura 2a 0 , es 500 kms -1 .

34. A principios de la década de 1920, era evidente que era necesaria una nueva mecánica, ya que las tentativas de introducir condiciones cuánticas a la mecánica de Newton no resultaban satisfactorias. Esta nueva mecánica debería considerar la naturaleza dual de las partículas elementales . A esta nueva mecánica se le llama Mecánica Cuántica o Mecánica Ondulatoria. MECANICA CUANTICA

35. Los nodos no sufren desplazamiento alguno. Ondas estacionarias: λ = n = 1, 2, 3… 2 π r = n λ 2L n

36. La función, ψ , psi, que describe el sistema se llama función de onda: Corresponde a una onda estacionaria dentro de los límites del sistema descrito.

37. Aunque la función de onda no tiene un sentido físico, su cuadrado representa la probabilidad de encontrar a la partícula en el espacio.

38. EL ÁTOMO DE HIDRÓGENO El átomo de hidrógeno es el único que se puede resolver exactamente, el resto solo se puede resolver en forma aproximada. Para ello se utilizan las funciones de onda encontradas para el átomo más simple: el hidrógeno . Entonces, la función de onda que es solución, se puede expresar en función de las coordenadas polares: Schrödinger, 1927 H ψ = E ψ

39. De la resolución de la ecuación de Schrödinger para el átomo de hidrógeno aparecen ciertos números que llamamos números cuánticos que definen la función de onda y cuantizan los estados de energía permitidos. n = número cuántico principal que determina la energía del electrón en el átomo de hidrógeno, y puede tomar los valores 1, 2, 3, ... l = número cuántico azimutal que cuantiza el momento angular orbital, y puede tomar valores de 1, 2, 3,....(n-1). m l = número cuántico magnético que cuantiza la componente del momento angular a lo largo del eje z, y puede tomar los valores de l, l-1, l-2, ...0, -1, -2, ....-l. Una función de onda, puede entonces especificarse en términos de los valores de los números cuánticos que las definen.  (r,  ,  ) =  (n,l,m l, m s )

40. Número cuántico n n = 1, 2, 3, 4, …. n=2 n=3 Distancia desde e - hasta el núcleo n=1

41. Número cuántico del momento angular l Dado un valor n , l = 0, 1, 2, 3, … n-1 n = 1, l = 0 n = 2, l = 0 o 1 n = 3, l = 0, 1, o 2 “ volumen” de espacio que ocupan los e - l = 0 orbital s l = 1 orbital p l = 2 orbital d l = 3 orbital f

42. l = 0 (orbitales s) l = 1 (orbitales p)

43. l = 2 (orbitales d)

44. Número cuántico magnético m l Dado un valor de l m l = - l , …., 0, …. + l Orientación del orbital en el espacio Si l = 1 (orbitales p), m l = -1, 0, o 1

45. Si l = 2 (orbitales d), m l = -2, -1, 0, 1, o 2

46. número cuántico de spin m s m s = + ½ o - ½ m s = - ½ m s = + ½

47. FORMA ANALÍTICA DE LOS ORBITALES ATÓMICOS.

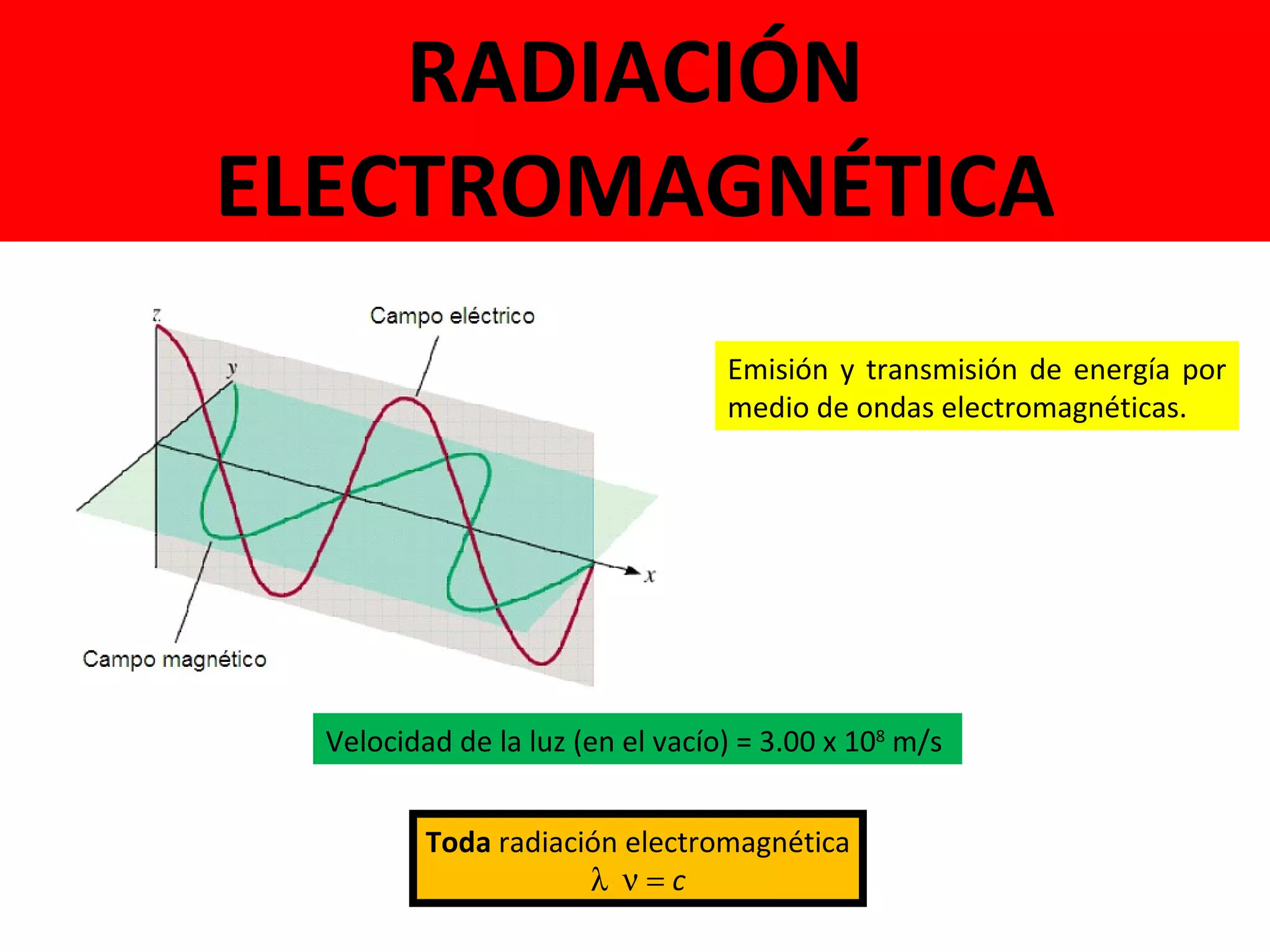
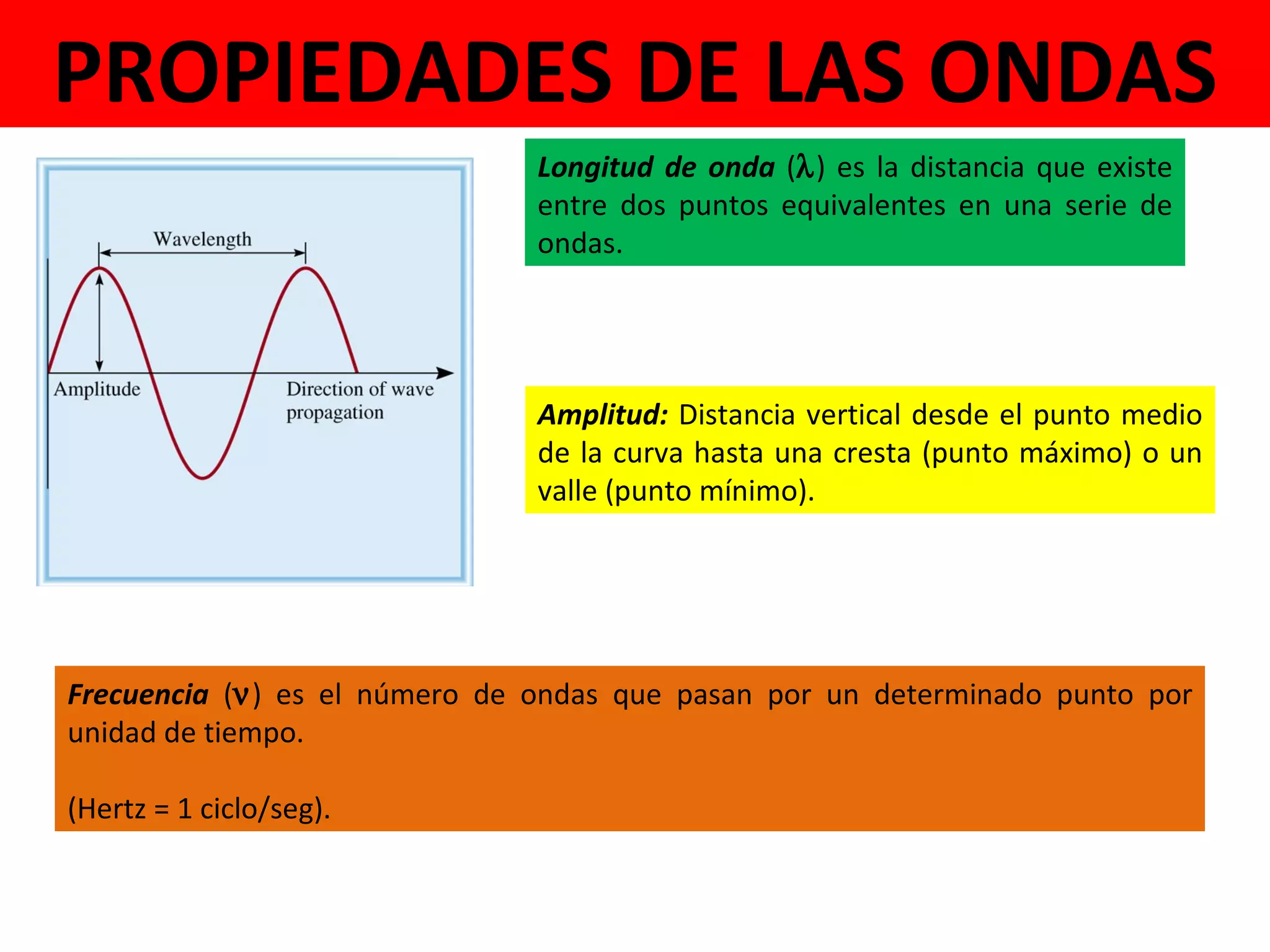
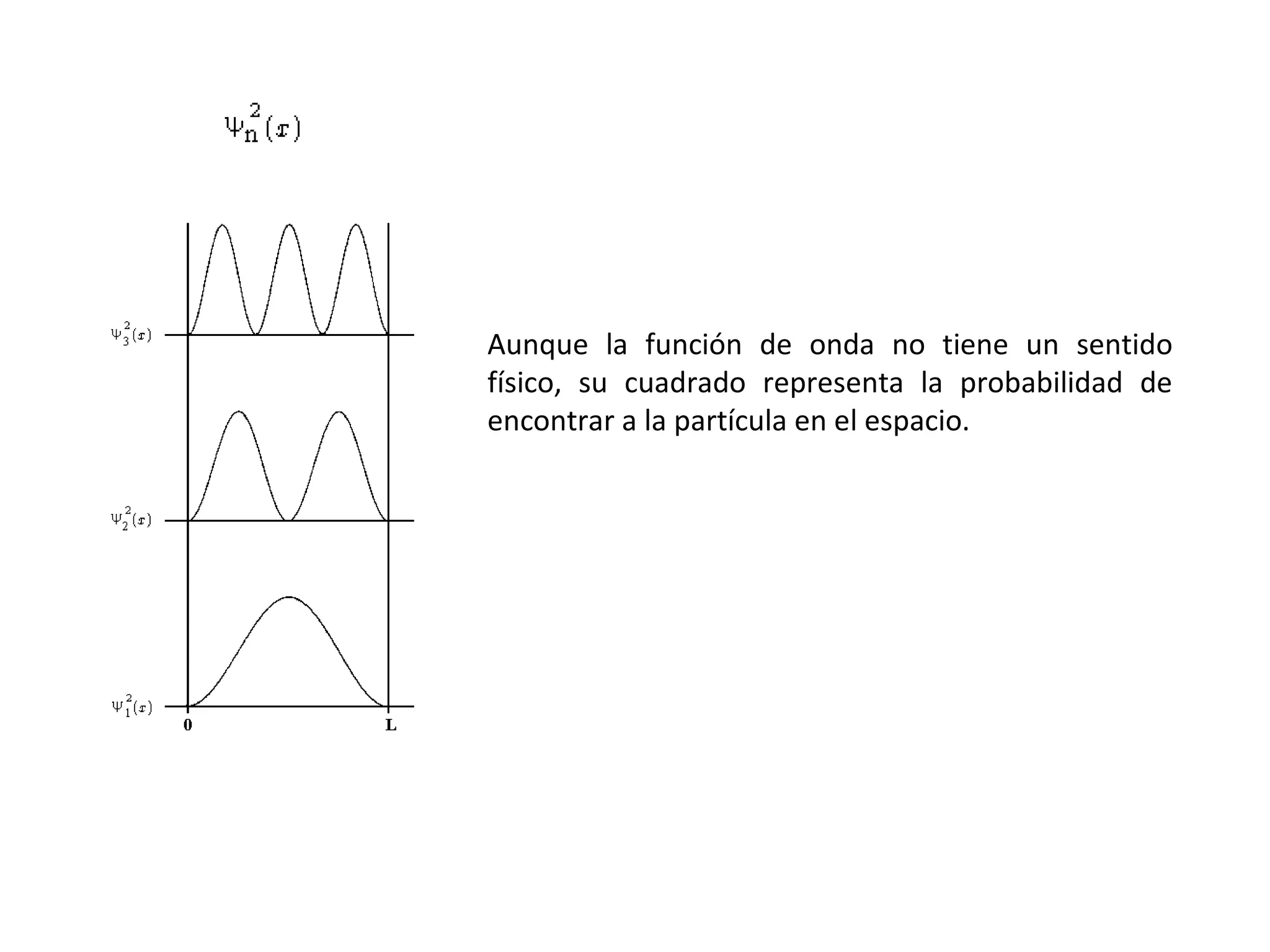
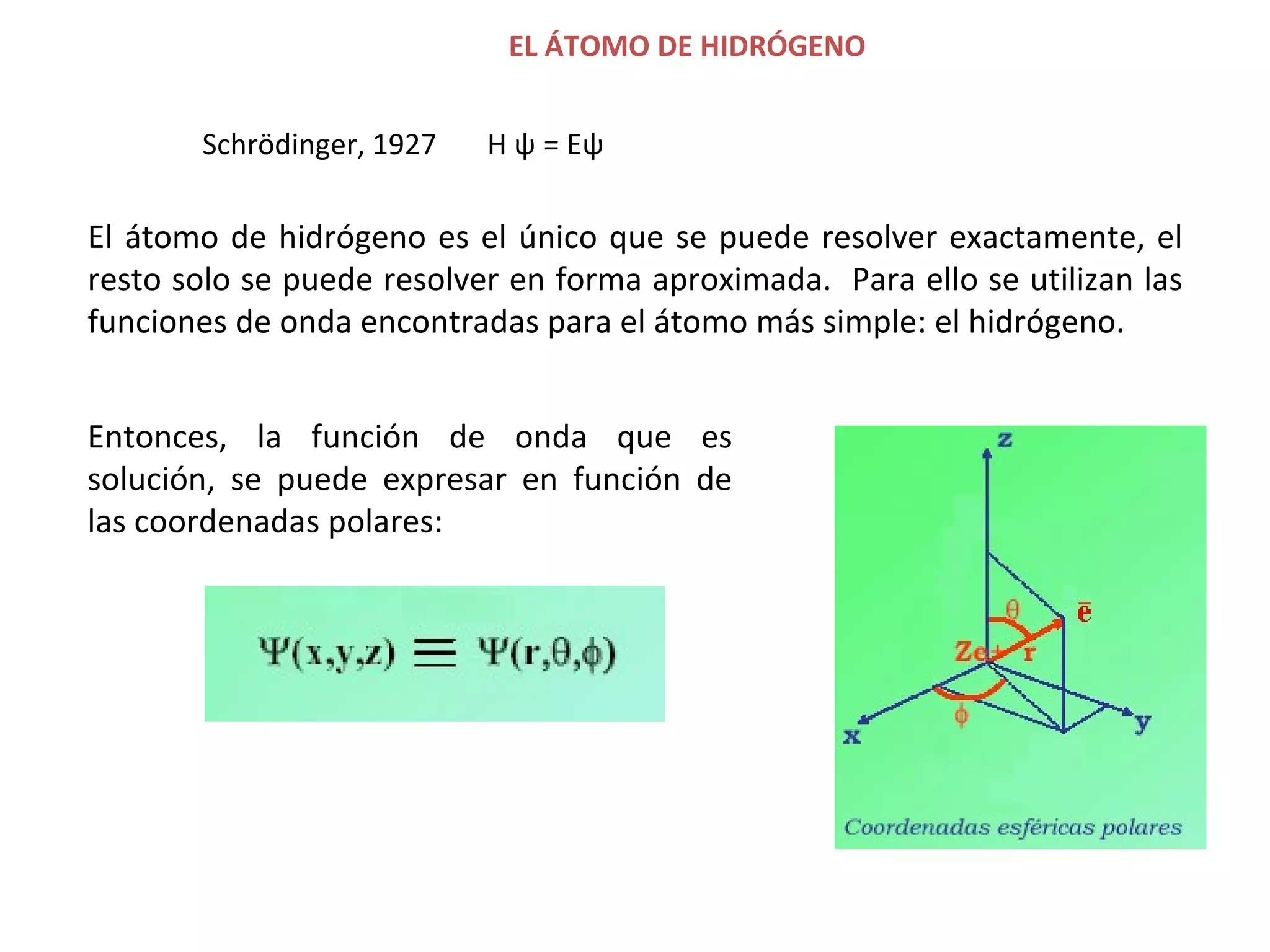
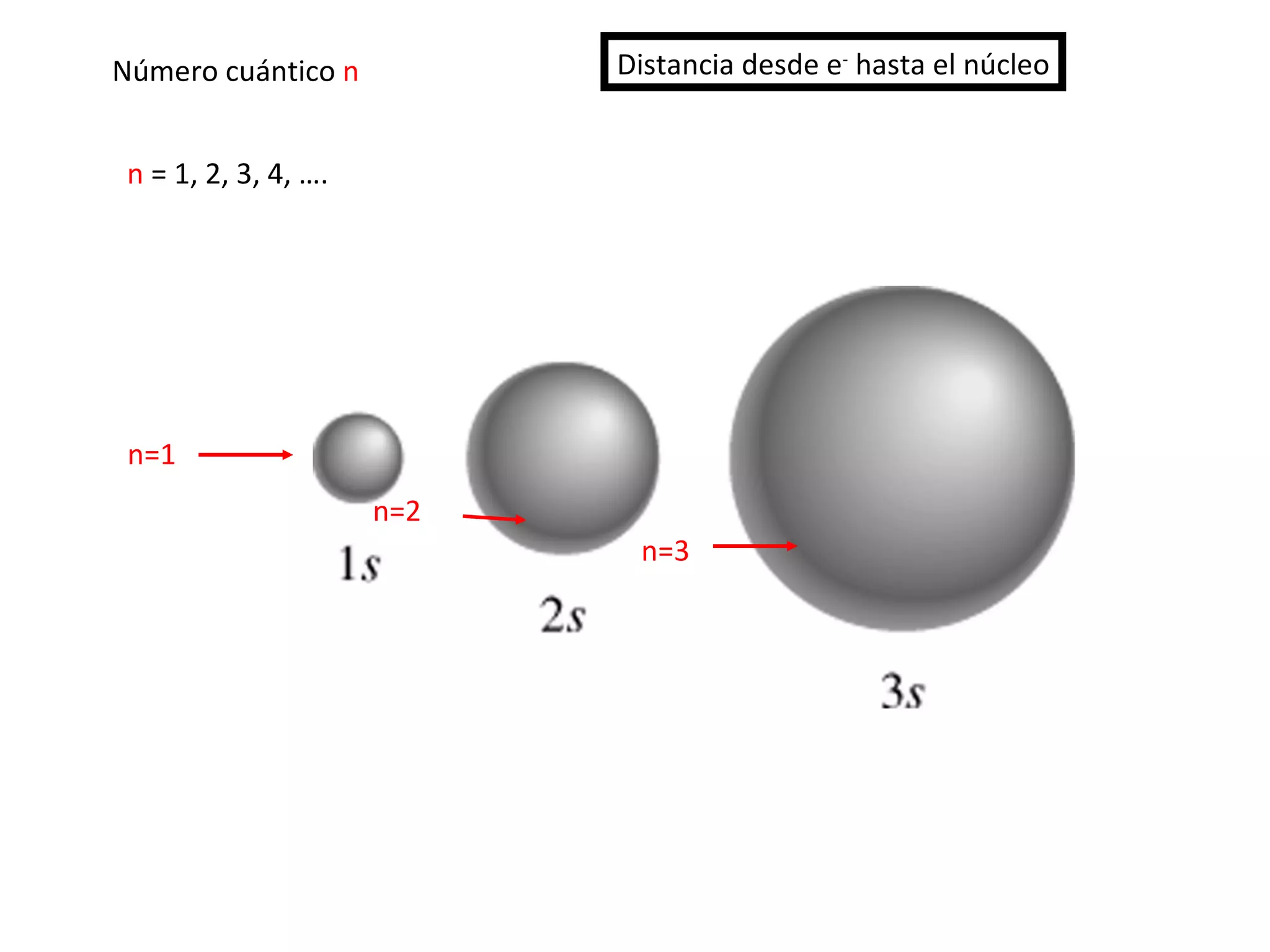
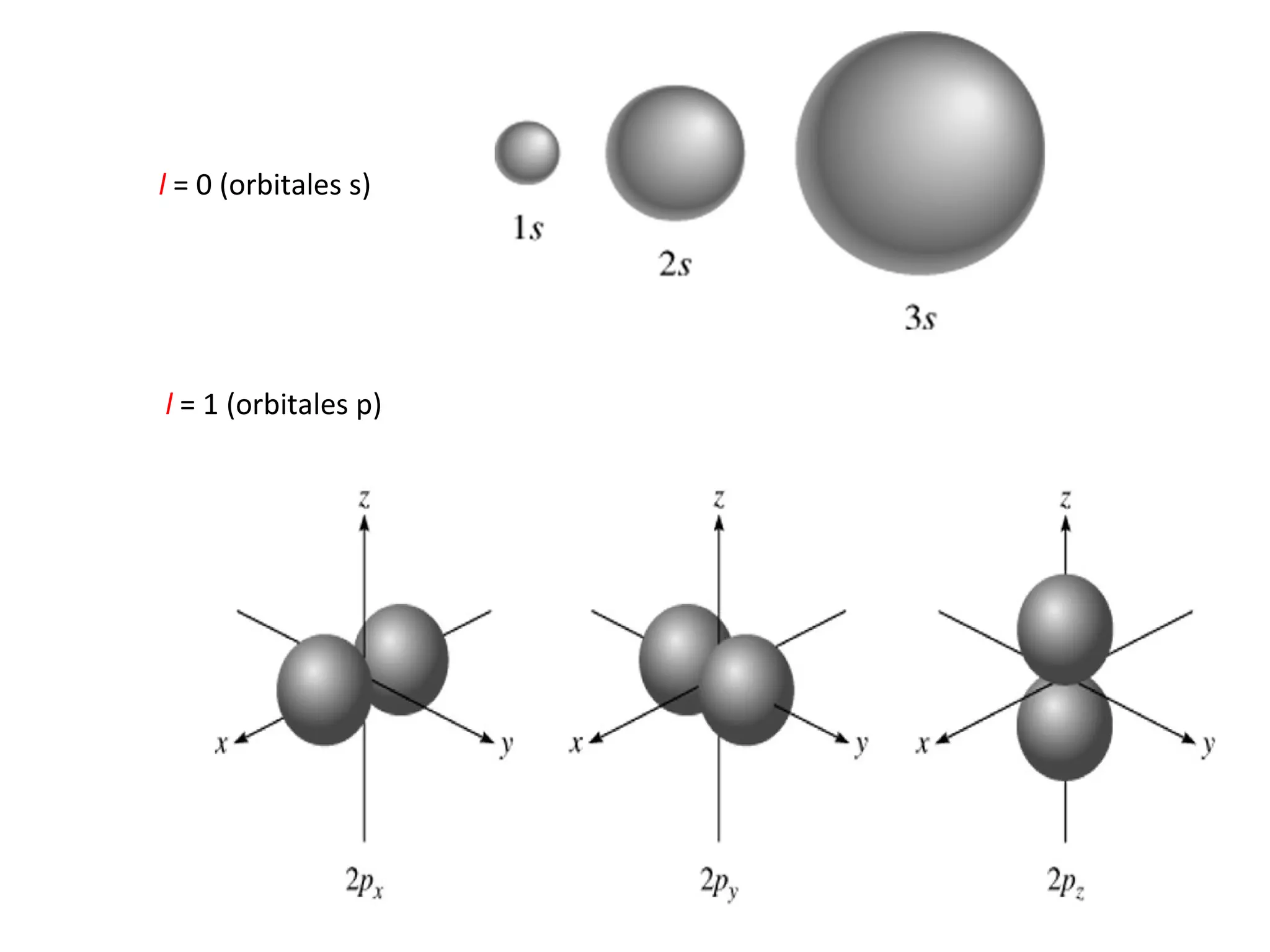
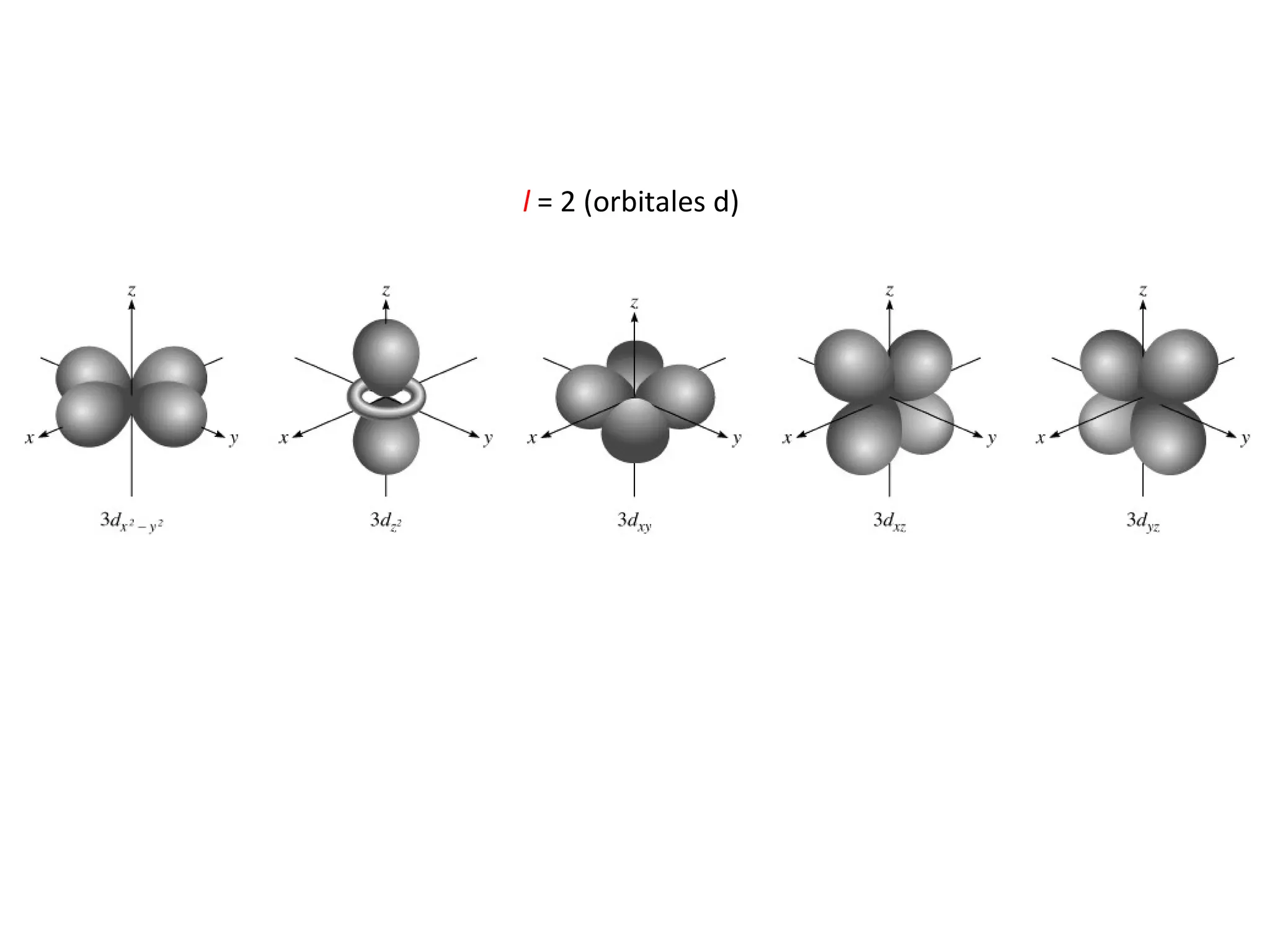
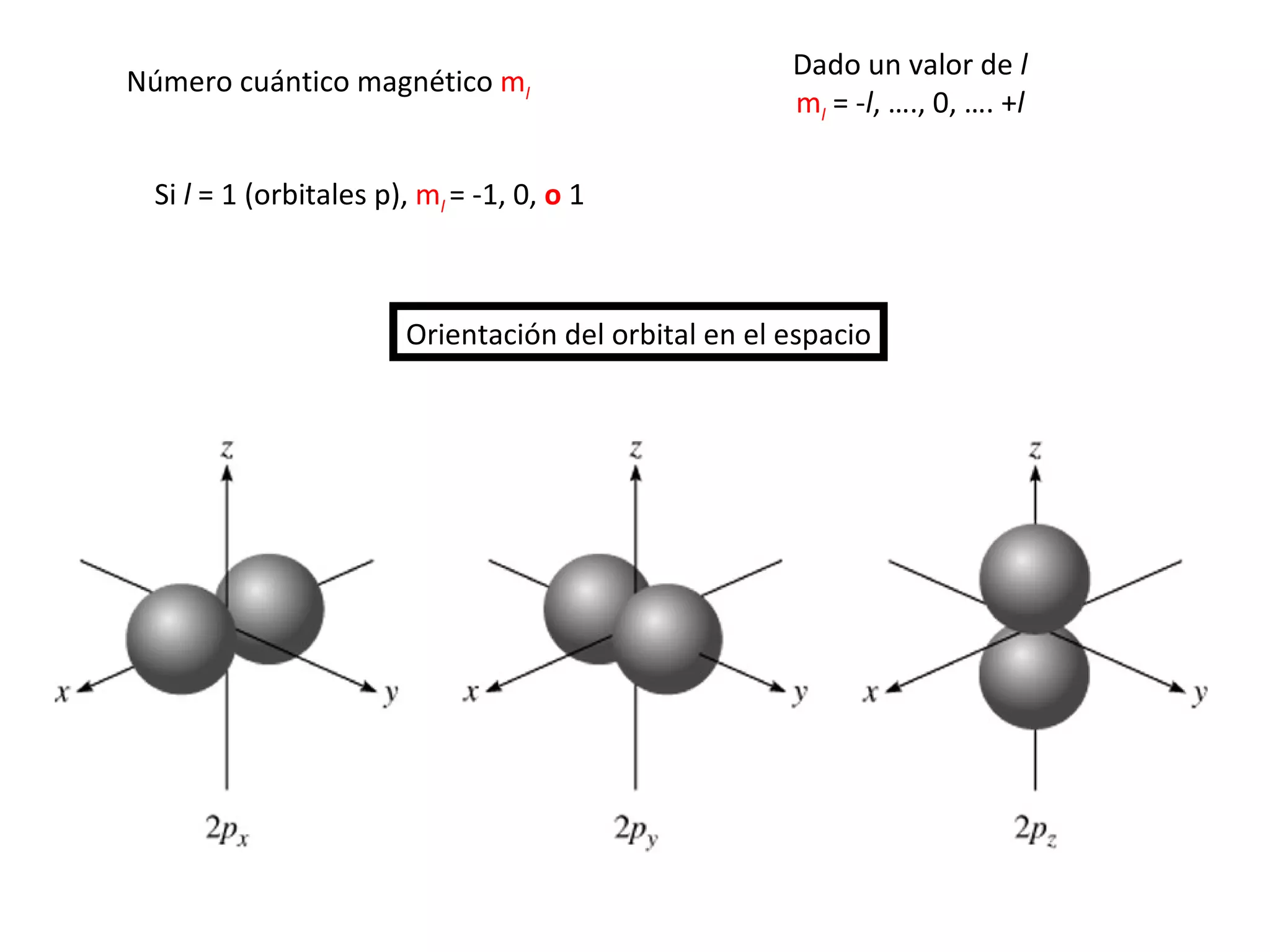
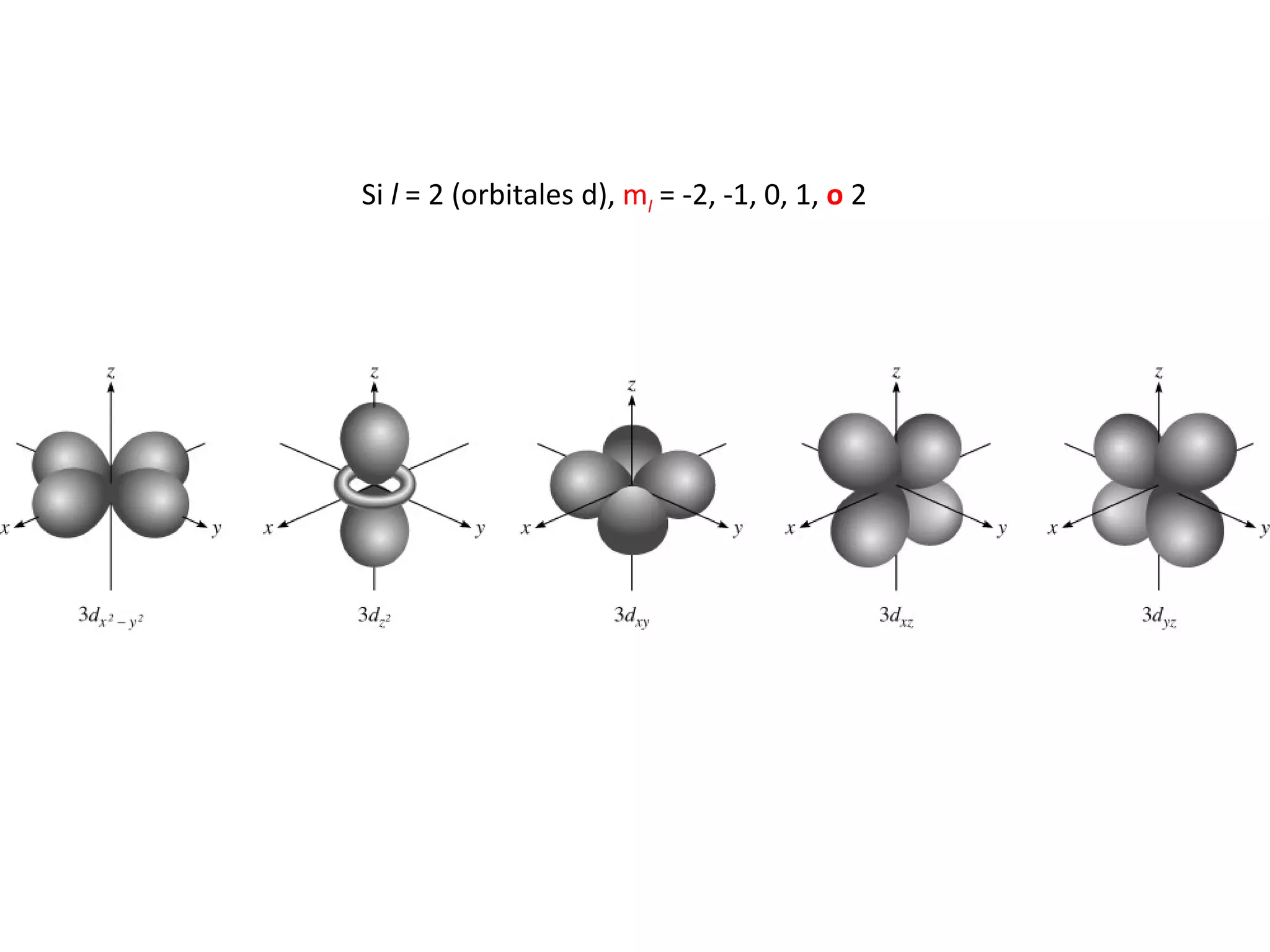
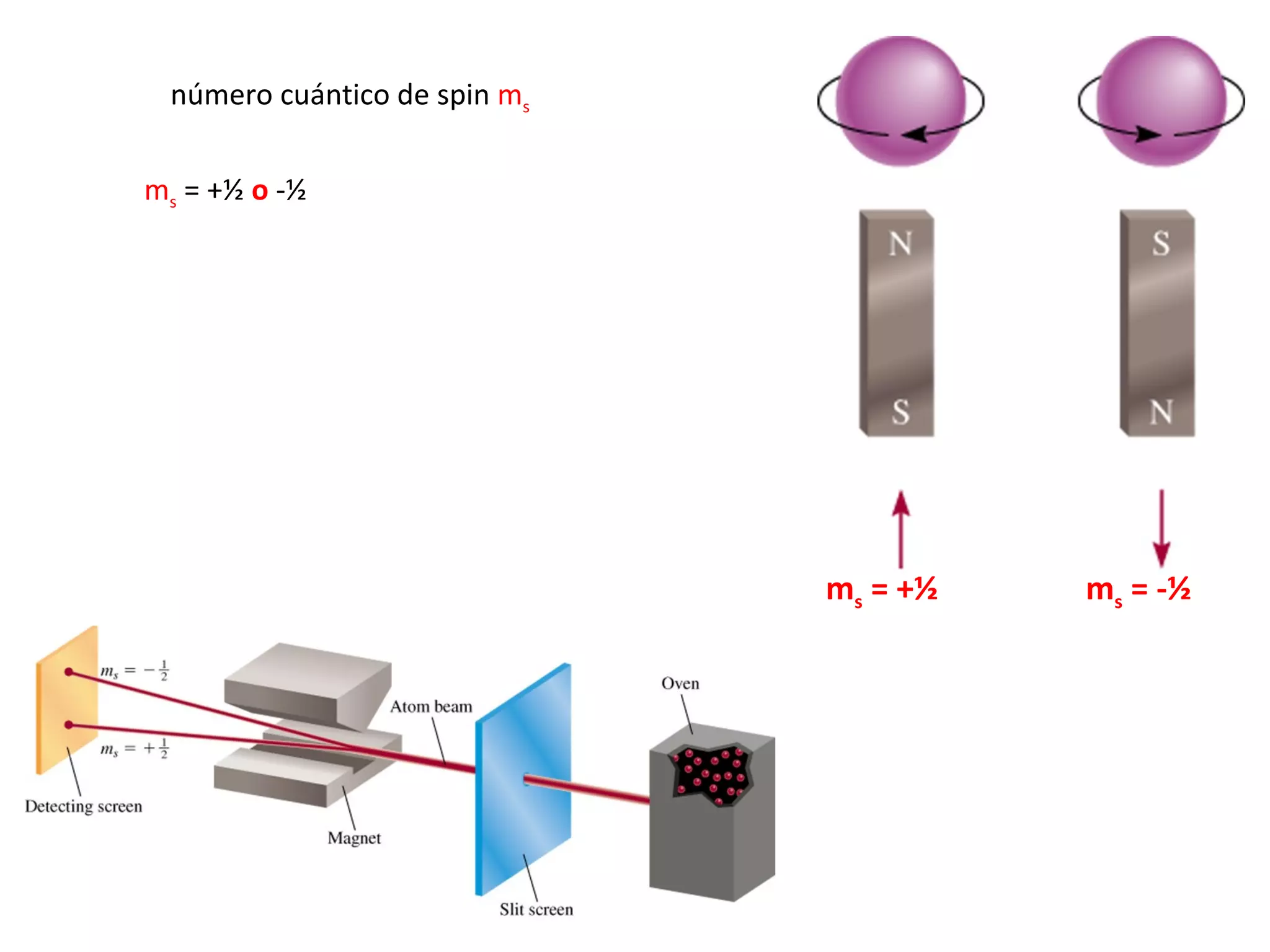
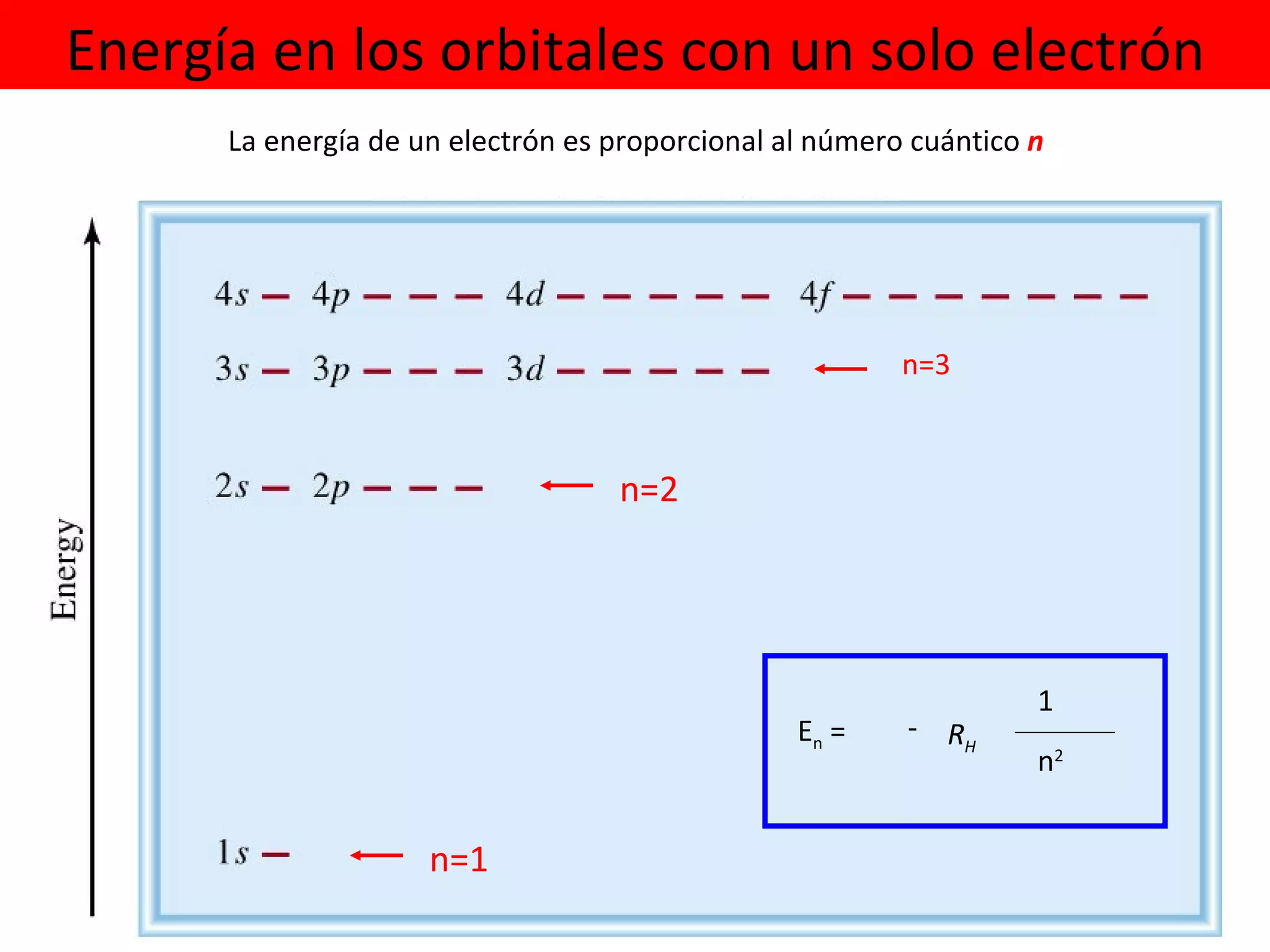
48. A cada estado de movimiento definido por la función de onda  le corresponde una determinada energía.  = fn(n, l , m l , m s ) El electrón en el átomo de hidrógeno queda descrito entonces por su función de onda. Para el átomo de hidrógeno la energía depende sólo del número cuántico n, y queda dada por: E n = - 1 2 Z 2 n 2 Unidades atómicas de energía E n = - 1 n 2 [Hartree] 1 [Hartree] = 4,36 x 10 -18 J R H R H = 2,18 x 10 -18 J H ψ = E ψ

49. Energía en los orbitales con un solo electrón La energía de un electrón es proporcional al número cuántico n E n = - 1 n 2 R H n=1 n=2 n=3

50. Nivel – electrones con el mismo valor de n Subnivel – electrones con el mismo valor de n y l Orbital – electrones con el mismo valor de n, l , y m l

51. Para describir completamente un electrón en un á tomo se requieren cuatro números cuánticos: n. l, m l y m s Ψ (total) = Ψ (n,l,m) m s

52. El único electrón en el átomo de hidrógeno, en el estado de más baja energía o estado basal (estado fundamental), queda descrito por la función de onda u orbital 1s. Se dice que la configuración electrónica del hidrógeno en su estado basal es 1s 1 . Los números cuánticos asociados son: n = 1; l = 0; ml = 0; ms = +½ o -½.

53. ÁTOMOS POLIELECTRÓNICOS Y CONFIGURACIÓN ELECTRÓNICA. La función de onda, Ψ, de un átomo de N electrones puede expresarse como el producto de las N funciones de onda de cada uno de esos electrones (orbitales) Se describen los electrones en átomos multi-electrónicos a través de las mismas funciones de onda encontradas para la descripción del electrón en el átomo de hidrógeno. Esta descripción de los electrones se denomina: configuración electrónica. ¿Cómo son las distribuciones electrónicas en los átomos polielectrónicos?

54. Principio de construcción (“aufbau” o “building-up”): En los átomos polielectrónicos en su configuración electrónica fundamental, las funciones de onda de sus diferentes electrones son aquellas que corresponden a los orbitales de menor energía. ¿Como varía la energía de los orbitales en un átomo con más de un electrón? ¿Cuántos electrones se pueden describir a través de la misma función de onda? o ¿Cuántos electrones pueden ocupar un orbital?

55. Principio de exclusión de Pauli – cada electrón en un átomo tiene sus propios números cuánticos, y no pueden existir dos e - en el mismo átomo con los mismos valores Si n, l, y m l están definidos, entonces m s = ½ o - ½  = (n, l , m l , ½ ) o  = (n, l , m l , - ½ ) Por lo tanto un orbital puede contener solo 2 electrones

56. ¿Como varía la energía de los orbitales en un átomo con más de un electrón? La energía depende de n + l n=1 l = 0 n=2 l = 0 n=2 l = 1 n=3 l = 0 n=3 l = 1 n=3 l = 2 n=4 l = 0

58. ¿Por qué esta dependencia de la energía? El efecto pantalla

59. Llenado de orbitales en átomos con más de un electrón. H 1 electrón H 1s 1 He 2 electrones He 1s 2 Li 3 electrones Li 1s 2 2s 1 Be 4 electrones Be 1s 2 2s 2 B 5 electrones B 1s 2 2s 2 2p 1 C 6 electrones La configuración electrónica ? ?

60. Regla de Hund C 6 electrones C 1s 2 2s 2 2p 2 N 7 electrones N 1s 2 2s 2 2p 3 O 8 electrones O 1s 2 2s 2 2p 4 F 9 electrones F 1s 2 2s 2 2p 5 Ne 10 electrones Ne 1s 2 2s 2 2p 6 El arreglo más estable de electrones en los subniveles se logra cuando se tiene el mayor número de “spins” paralelos.

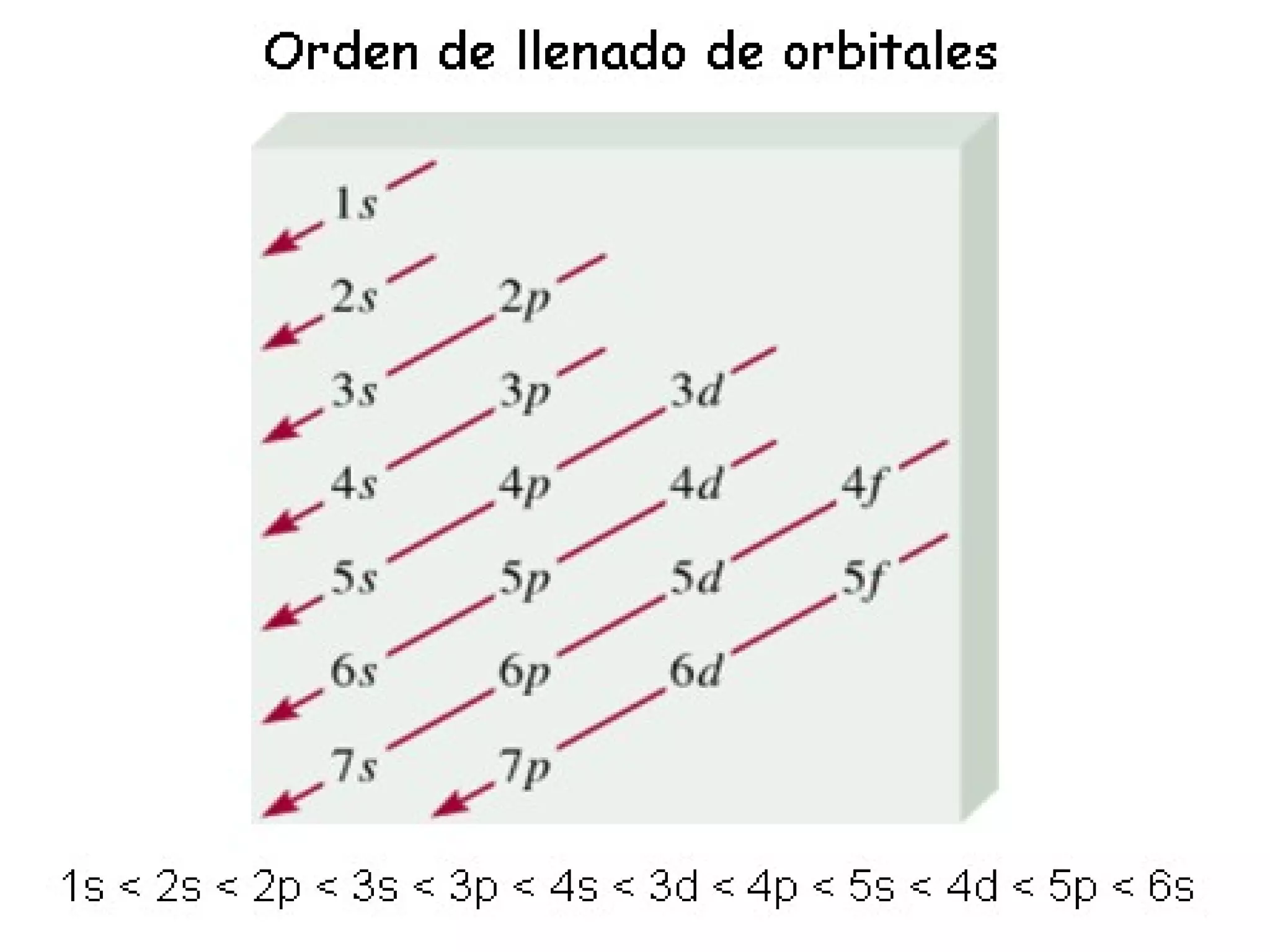
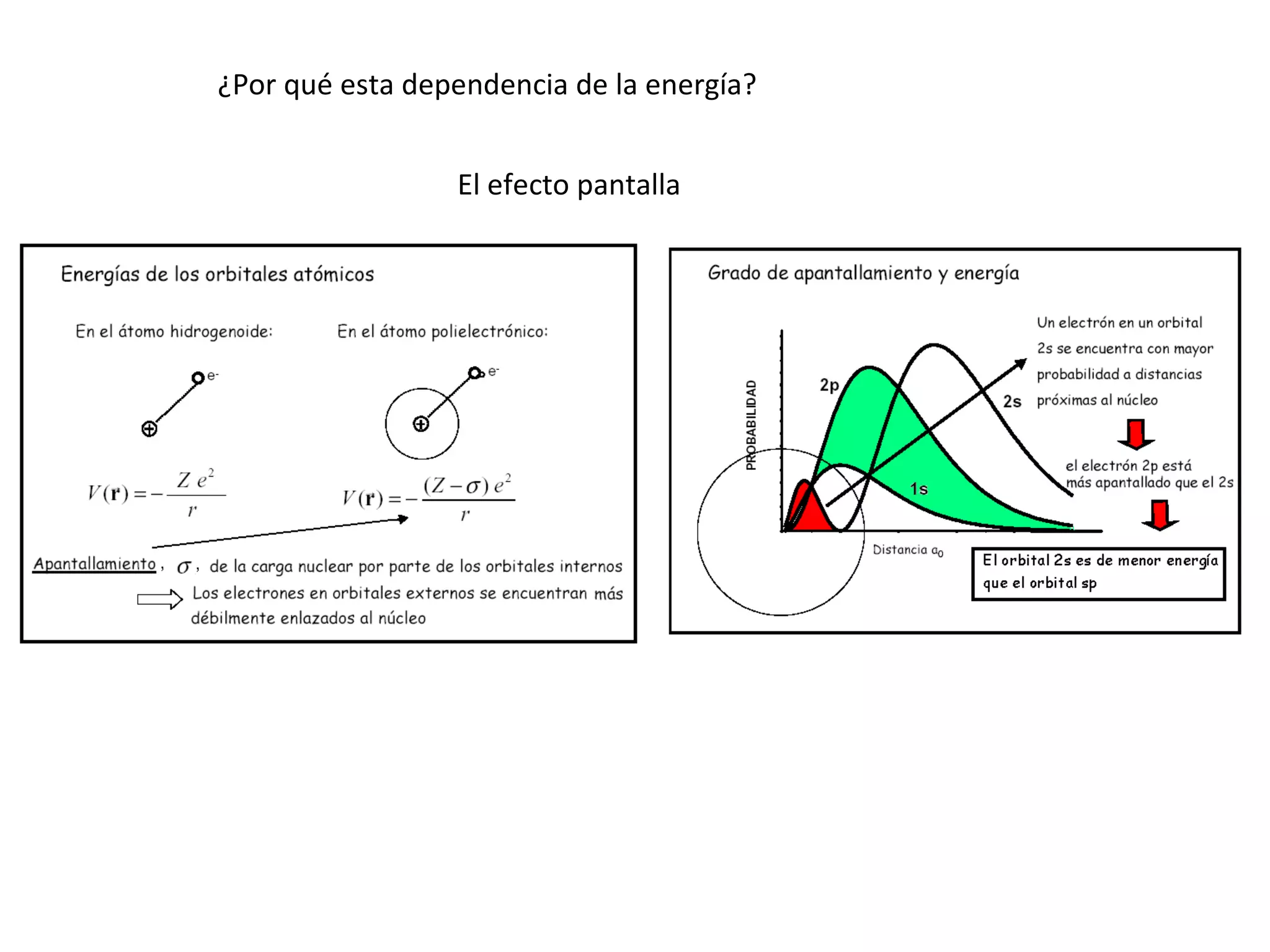
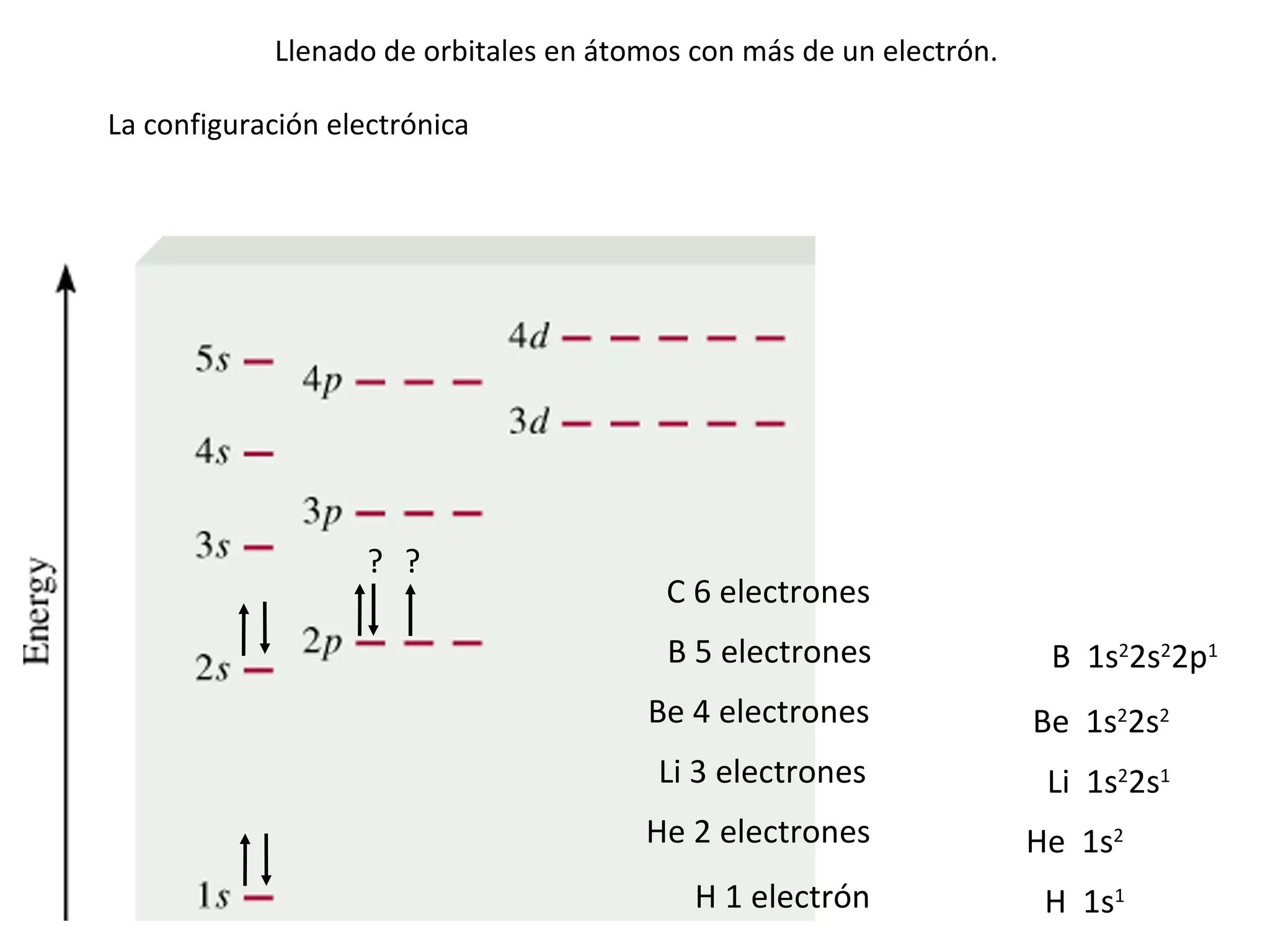
61. Algunas configuraciones electrónicas: Cr [Ar]4s 1 3d 5 y no [Ar]4s 2 3d 4 Cu, Ag, Au : [ ] ns 1 (n-1)d 10 y no [ ] ns 2 (n-1)d 9 Ni [Ar] 4s 2 3d 8 Pd [ Kr ] 5 s 1 4 d 9 Pt [ Kr ] 5 d 10 Ni 2+ [Ar] 4s 0 3d 8 Ni 2+ [Ar] 3d 8 En general las situaciones de capa llena o semillena son de mayor estabilidad y de menor energía.

62. La diferente distribución radial de los diferentes orbitales hace que las constantes de pantalla dependan de cada tipo de orbital y por tanto los orbitales con igual valor de n y distinto valor de l dejan de ser orbitales degenerados. Orbitales hidrogenoides modificados Z i = Z ef,i Energía del orbital i :

64. Los electrones m á s externos de un átomo constituyen sus: ELECTRONES DE VALENCIA El resto de sus electrones constituyen su: N úcleo Electrónico o Electrones Internos El número de electrones de valencia de un átomo condiciona su : Valencia Química (capacidad para combinarse con otros elementos) Si un átomo tiene toda su capa de valencia completa se dice que tiene configuración de capa cerrada o de Gas Noble . Gran estabilidad química. En su combinación con otros elementos (formación de moléculas), la tendencia del àtomo es hacia la adquisición de su configuración en capa completa, cediendo electrones, aceptando electrones o compartiendo electrones con los otros elementos. Elementos representativos : forman los electrones de valencia los ns y los np Elementos del bloque d : forman los electrones de valencia los ns y los (n-1)d . Elementos del bloque f : forman los electrones de valencia los ns , el (n-1)d y los (n-2)f .