Derivadas
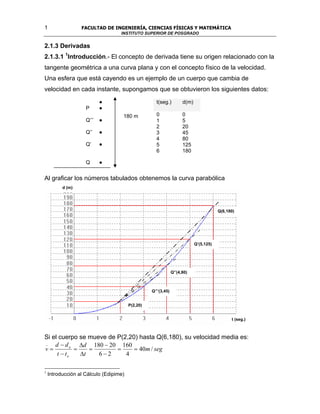
- 1. 1 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 2.1.3 Derivadas 2.1.3.1 1Introducción.- El concepto de derivada tiene su origen relacionado con la tangente geométrica a una curva plana y con el concepto físico de la velocidad. Una esfera que está cayendo es un ejemplo de un cuerpo que cambia de velocidad en cada instante, supongamos que se obtuvieron los siguientes datos: ● t(seg.) d(m) P ● 180 m 0 0 Q’’’ ● 1 5 2 20 Q’’ ● 3 45 4 80 Q’ ● 5 125 6 180 Q ● Al graficar los números tabulados obtenemos la curva parabólica d (m) Q(6,180) Q’(5,125) Q’’(4,80) Q’’’(3,45) P(2,20) t (seg.) Si el cuerpo se mueve de P(2,20) hasta Q(6,180), su velocidad media es: _ d − d o ∆d 180 − 20 160 v= = = = = 40m / seg t − to ∆t 6−2 4 1 Introducción al Cálculo (Edipime)
- 2. 2 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO ↔ En la gráfica, este valor representa la pendiente de la recta secante PQ . Si el cuerpo se mueve desde P hasta Q’ su velocidad media es: _ ∆d 125 − 20 105 v= = = = 35m / seg ∆t 5−2 3 ↔ Este valor representa la pendiente de la recta secante PQ' , en la misma forma cuando se mueve de P hasta Q’’ y de P hasta Q: _ ∆d 80 − 20 _ ∆d 45 − 20 v= = = 30m / seg y v = = = 25m / seg ∆t 4−2 ∆t 3− 2 ↔ ↔ Estos valores representan las pendientes de la rectas secantes PQ' ' y PQ' ' ' . Las velocidades medias: 40 m/seg., 35 m/seg., 30 m/seg., 25 m/seg., pendientes ↔ ↔ ↔ ↔ de las rectas secantes PQ , PQ' , PQ' ' , PQ' ' ' , se acercarán en estos diferentes pasos a la definición de velocidad instantánea en el punto P. ↔ En el límite cuando Q' ' ' se confunde con P., la recta secante PQ' ' ' se transforma en la “recta tangente” a la curva en el punto P y la velocidad instantánea es la pendiente de la recta tangente en el punto P. 2.1.3.2 2Interpretación geométrica y= f(x) Q( x + ∆x, y + ∆y ) T P ( x, y ) ∆y ∆x ∆y La figura muestra que es la pendiente de la secante que une un punto fijo ∆x P( x, y ) cualquiera de la curva con otro Q( x + ∆x, y + ∆y ) . Cuando ∆x → 0 , P permanece fijo y Q se mueve sobre la curva acercándose a P; la recta PQ va 2 Cálculo (Schaums)
- 3. 3 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO girando alrededor de P hasta que llega a su posición límite que es la tangente PT a la curva en el punto P. dy Así pues dx es la pendiente de la tangente a la curva y = f(x) en el punto P La pendiente de la recta tangente en el punto P es: lim ∆y m tan = ó ∆x → 0 ∆x lim f ( x + h) − f ( x ) m tan = cuando el límite existe. h→0 h 2.1.3.2 Calculo de la derivada Se puede calcular la derivada de una función por dos métodos: a) Por definición de límite b) Por reglas. 2.1.3.2.1 Calculo de la derivada por definición de límite Para calcular la derivada de una función por la 3definición de límite, se pueden seguir los siguientes cuatro pasos: Dada la función y = f (x) 1. Determinar f ( x + h) 2. Efectuar f ( x + h) − f ( x) f ( x + h) − f ( x ) 3. Dividir por h para obtener: h 4. Calcular el límite cuando h → 0 para obtener m lim f ( x + h) − f ( x ) m= h→0 h 2.1.3.2.1.1 Ejemplos a) Hallar la derivada de y = x 2 3 Introducción al Cálculo (Edipime)
- 4. 4 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO Aplicamos el método: 1. Determinar f ( x + h) f ( x + h) = ( x + h) 2 2. Efectuar f ( x + h) − f ( x) ( x + h) 2 − x 2 f ( x + h) − f ( x ) 3. Dividir por h para obtener: h ( x + h) 2 − x 2 h 4. Calcular el límite cuando h → 0 para obtener m lim f ( x + h) − f ( x ) m= h→0 h ( x + h) 2 − x 2 lim m= h→0 h lim x 2 + 2 xh + h 2 − x 2 m= , desarrollando el cuadrado del binomio h→0 h 2 xh + h 2 lim m= , sacando factor común h h→0 h lim h( 2 x + h) m= , simplificando h→0 h lim m= 2 x + h , evaluamos el límite h→0 lim m= = 2x + 0 h→0 m = 2x b) Hallar la derivada de f ( x) = 2 x + 3 Aplicamos el método: 1. Determinar f ( x + h)
- 5. 5 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO f ( x + h) = 2( x + h) + 3 2. Efectuar f ( x + h) − f ( x) [2( x + h) + 3] − [2 x + 3] f ( x + h) − f ( x ) 3. Dividir por h para obtener: h [2( x + h) + 3] − [2 x + 3] h 4. Calcular el límite cuando h → 0 para obtener m lim f ( x + h) − f ( x ) m= h→0 h lim [2( x + h) + 3] − [2 x + 3] m= h→0 h lim 2 x + 2h + 3 − 2 x − 3 m= , destruyendo paréntesis h→0 h lim 2h m= , términos semejantes h→0 h lim m= 2 , simplificando h→0 lim m= 2 , evaluamos el límite h→0 m=2 c) Hallar la derivada de f ( x) = x Aplicamos el método: 1. Determinar f ( x + h) f ( x + h ) = ( x + h)
- 6. 6 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 2. Efectuar f ( x + h) − f ( x) x+h − x f ( x + h) − f ( x ) 3. Dividir por h para obtener: h x+h − x h 4. Calcular el límite cuando h → 0 para obtener m lim f ( x + h) − f ( x ) m= h→0 h lim x+h − x m= h→0 h lim x+h − x x+h + x m= * , multiplicamos por la conjugada h→0 h x+h + x lim ( x + h)2 − ( x)2 m= , factorando la diferencia de cuadrados h → 0 h( x + h + x ) lim x+h−x m= , simplificando h → 0 h( x + h + x ) lim h m= , simplificando h → 0 h( x + h + x ) lim 1 m= , simplificando h → 0 ( x + h + x) lim 1 1 1 m= = = = , evaluando el límite h→0 ( x + 0 + x) ( x + x) 2 x 1 m= 2 x
- 7. 7 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 2x − 3 d) Hallar la derivada de f ( x) = 3x + 4 Aplicamos el método: 5. Determinar f ( x + h) 2( x + h) − 3 f ( x + h) = 3( x + h) + 4 6. Efectuar f ( x + h) − f ( x) [2( x + h) − 3] [2 x − 3] − [3( x + h) + 4] [3x + 4] f ( x + h) − f ( x ) 7. Dividir por h para obtener: h [2( x + h) − 3] [2 x − 3] − [3( x + h) + 4] [3x + 4] h 8. Calcular el límite cuando h → 0 para obtener m lim f ( x + h) − f ( x ) m= h→0 h [2( x + h) − 3] [2 x − 3] − lim [3( x + h) + 4] [3x + 4] m= h→0 h [2 x + 2h − 3] [2 x − 3] − lim [3x + 3h + 4] [3x + 4] m= , destruyendo paréntesis h→0 h [3x + 4][2 x + 2h − 3] − [3x + 3h + 4][2 x − 3] lim [3x + 3h + 4][3x + 4] m= , sacando mcm h→0 h 6 x 2 + 6 xh − 9 x + 8 x + 8h − 12 − [6 x 2 − 9 x + 6 xh − 9h + 8 x − 12] lim [3 x + 3h + 4][3x + 4] m= h , h→0
- 8. 8 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 6 x 2 + 6 xh − 9 x + 8 x + 8h − 12 − 6 x 2 + 9 x − 6 xh + 9h − 8 x + 12 lim [3 x + 3h + 4][3 x + 4] m= h , h→0 8h + 9h lim [3x + 3h + 4][3x + 4] m= h , términos semejantes h→0 17h lim [3x + 3h + 4][3x + 4] m= h , términos semejantes h→0 1 17h lim [3x + 3h + 4][3x + 4] m= h , simplificamos h→0 1 lim 17 m= [3x + 3h + 4][3x + 4] , simplificamos h→0 lim 17 17 17 m= = = [3x + 3(0) + 4][3x + 4] [3x + 4][3x + 4] [3x + 4] 2 , evaluamos el límite h→0 17 m= [3x + 4] 2 2.1.3.2.1.2 Ejercicios propuestos
- 9. 9 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 1 1. Hallar la derivada de y= 2 x + 1 , Sol. 2x + 1 3 1 2. Hallar la derivada de y= x , Sol. 3 x2 3 3. Hallar la derivada de y= x 2 + 3x + 5 , Sol. 2 x + 3 1 + 2x 1 4. Hallar la derivada de y= , Sol. 1 − 2x 2( x + 1) 2 2.1.3.2.2 Calculo de la derivada por reglas 4 En los ejercicios anteriores se calculó la derivada por la definición dada de límite, este procedimiento es bastante laborioso. Sin embargo se pueden encontrar reglas que permiten calcular las derivadas fácilmente sin usar los pasos dados por la definición de límite. 5 Las funciones que aparecen en el cálculo elemental son, en general, derivables en sus intervalos de definición, pudiendo no serlo en algún punto aislado La nomenclatura que usaremos será: dy , f ' ( x) , y ' dx Algunas de las reglas que usaremos serán: 1. Derivada de una función constante f ( x) = c , donde c es una constante f ' ( x) = 0 2. Derivada de una función elevada a un exponente Si f ( x) = x n , para algún número natural, entonces: 4 f ' ( x) = nx n −1 Introducción al Cálculo (Edipime) 5 Cálculo (Schaums)
- 10. 10 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 3. Derivada de una función lineal Si f ( x) = x , la derivada de la función lineal es 1: f ' ( x) = 1 4. Derivada de una suma de funciones Si f y g son derivables en x , entonces f + g es también derivable en x , y: ( f + g )' ( x) = f ' ( x) + g ' ( x) 5. Derivada de un producto de funciones Si f y g son derivables en x , entonces f * g es también derivable en x , y: ( f * g )' ( x) = f ' ( x) g ( x) + g ' ( x) f ( x) 6. Caso especial del producto: cuando una función es constante [cf ( x)]' = c * f ' ( x) 7. Derivada de un Cociente de funciones f Si f y g son derivables en x y g ( x) ≠ 0 , entonces es derivable en x , g y: f f ' ( x) g ( x) − g ' ( x) f ( x) ( )' ( x) = g [ g ( x)] 2 8. Caso especial del cociente: cuando una función es constante c c * f ' ( x) [ ]' = − f ( x) [ f ( x)] 2 2.1.3.2.2.1 Ejemplos
- 11. 11 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO Hallar la derivada de: a) f ( x) = 5 x 4 , (Regla 6, constante por función) [cf ( x)]' = c * f ' ( x) f ' ( x) = 5 * 4 x 4 −1 f ' ( x) = 20 x 3 b) f ( x) = x 3 + x , (Reglas 2 y 3, función elevada a exponente y función lineal) f ' ( x) = nx n −1 y f ' ( x) = 1 f ' ( x) = 3x 2 −1 + 1 f ' ( x) = 3 x 2 + 1 1 c) g ( x) = , (Regla 8, caso especial de cociente de funciones) 5x − 3 2 c c * f ' ( x) [ ]' = − f ( x) [ f ( x)] 2 1(5 x 2 − 3)' g ' ( x) = − (5 x 2 − 3) 2 1(5 * 2 x 2 −1 − 0) g ' ( x) = − (5 x 2 − 3) 2 1(10 x) g ' ( x) = − (5 x 2 − 3) 2 10 x g ' ( x) = − (5 x 2 − 3) 2 d) h( x) = ( x 2 + 2)(3 x − 1) , (Regla 5, producto de funciones) ( f * g )' ( x) = f ' ( x) g ( x) + g ' ( x) f ( x)
- 12. 12 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO h' ( x) = ( x 2 + 2)' (3x − 1) + (3x − 1)' ( x 2 + 2) h' ( x) = (2 x 2 −1 + 0)(3x − 1) + (3 − 0)( x 2 + 2) h' ( x) = (2 x)(3x − 1) + (3x)( x 2 + 2) h' ( x) = (6 x 2 − 2 x) + (3x 2 + 6) h' ( x ) = 6 x 2 − 2 x + 3 x 2 + 6 h' ( x ) = 9 x 2 − 2 x + 6 3x 2 + 1 e) t ( x) = 2 , (Regla 7, cociente de funciones) 5x − 2 f f ' ( x) g ( x) − g ' ( x) f ( x) ( )' ( x) = g [ g ( x)] 2 (3x 2 + 1)'*(5 x 2 − 2) − (5 x 2 − 2)'*(3 x 2 + 1) t ' ( x) = (5 x 2 − 2) 2 (3 * 2 x 2 −1 + 0) * (5 x 2 − 2) − (5 * 2 x 2 −1 − 0)(3x 2 + 1) t ' ( x) = (5 x 2 − 2) 2 (6 x) * (5 x 2 − 2) − (10 x)(3x 2 + 1) t ' ( x) = (5 x 2 − 2) 2 (30 x 3 − 12 x) − (30 x 3 + 10 x) t ' ( x) = (5 x 2 − 2) 2 30 x 3 − 12 x − 30 x 3 − 10 x t ' ( x) = (5 x 2 − 2) 2 30 x 3 − 12 x − 30 x 3 − 10 x t ' ( x) = (5 x 2 − 2) 2 − 22 x t ' ( x) = (5 x 2 − 2) 2 2.1.3.2.2.2 Ejercicios propuestos
- 13. 13 FACULTAD DE INGENIERÍA, CIENCIAS FÍSICAS Y MATEMÁTICA INSTITUTO SUPERIOR DE POSGRADO 1. Hallar la derivada de y = 4 + 2 x − 3x 2 − 5 x 3 + 8 x 4 + 9 x 5 , Sol. 2 − 6 x − 15 x 2 − 32 x 3 + 45 x 4 1 2 1 2. Hallar la derivada de y = 3 3x 2 − , Sol. + 3 5x 9x 2 x 5x 3. Hallar la derivada de s = (t 2 − 3) 4 , Sol. 8t (t 2 − 3) 3 4. Hallar la derivada de y= y = ( x 2 + 4) 2 (2 x 3 − 1) 3 , Sol. 2 x( x 2 + 4)(2 x 3 − 1) 2 (13x 3 + 36 x − 2) x+3 5. Hallar la derivada de y= x 2 +6 x + 3 , Sol. x 2 +6 x + 3 3 − 2x − 12 6. Hallar la derivada de y= y = , Sol. 3 + 2x (3 + 2 x) 2