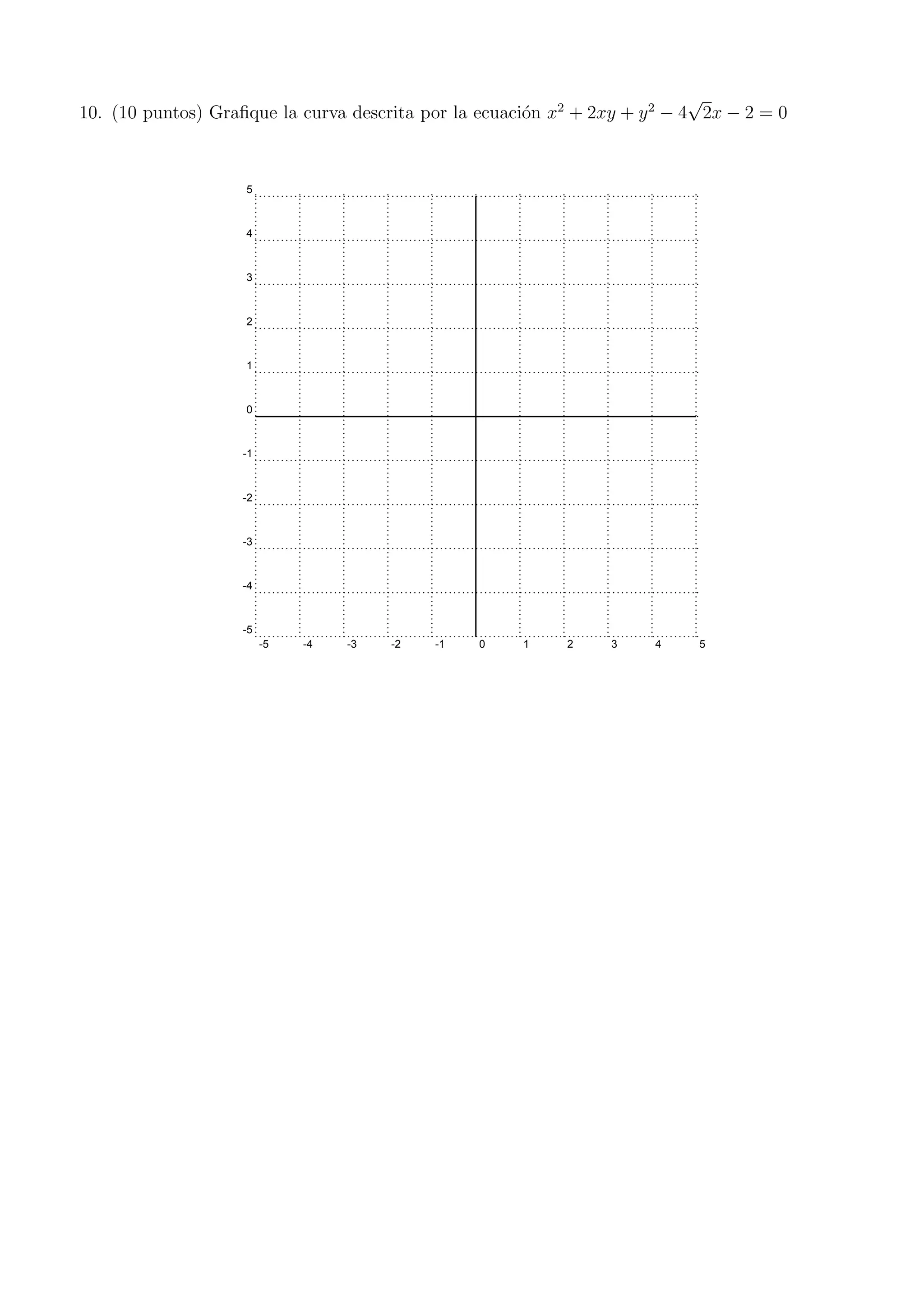
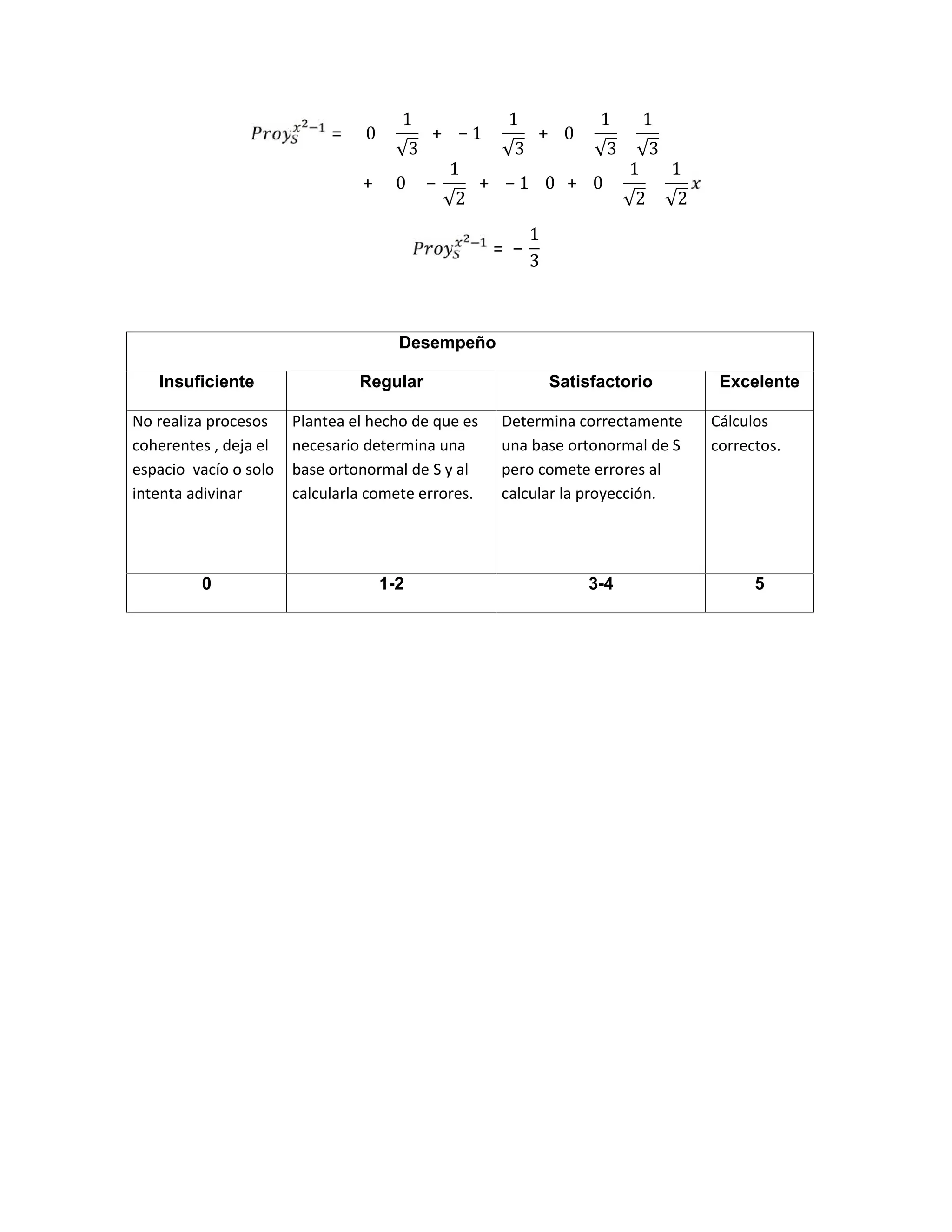
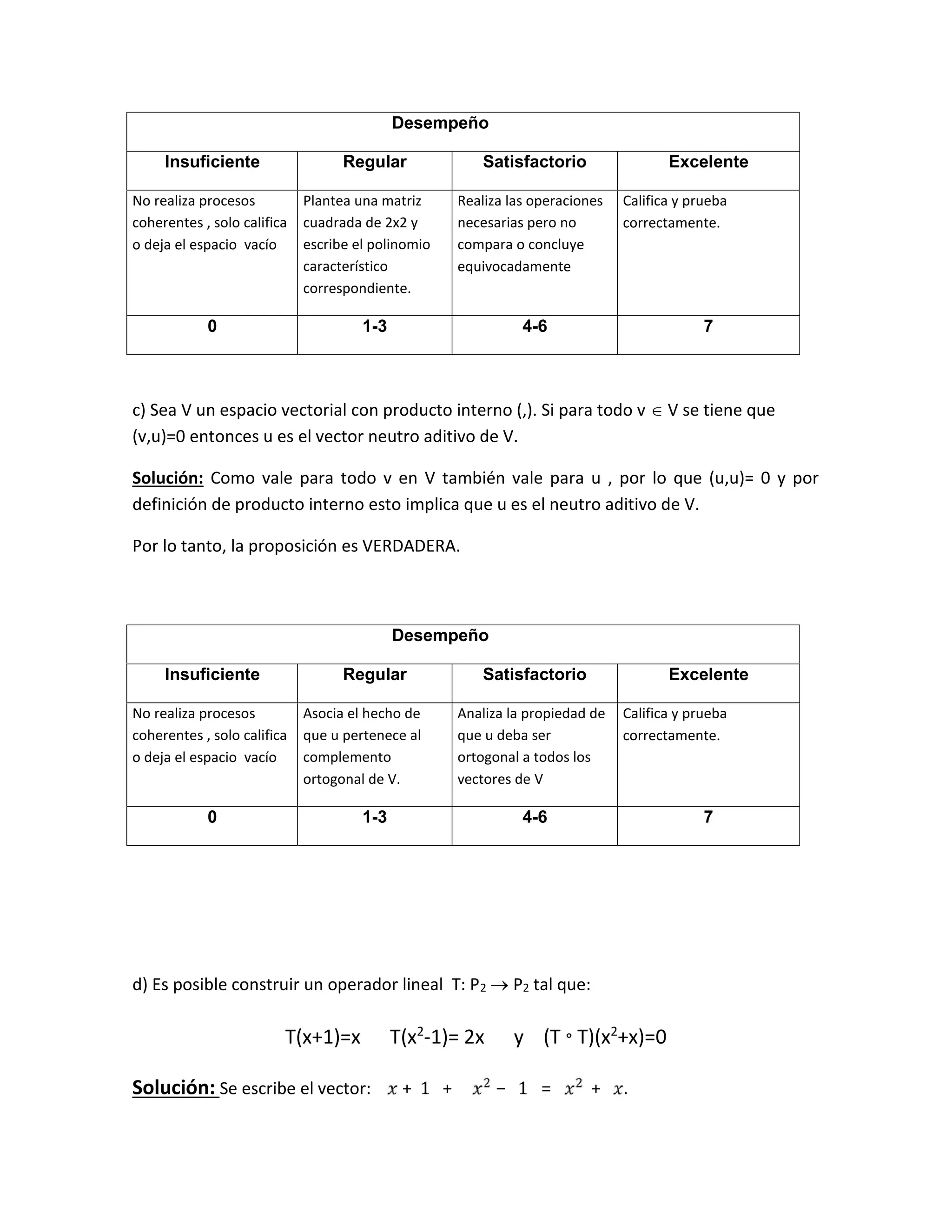
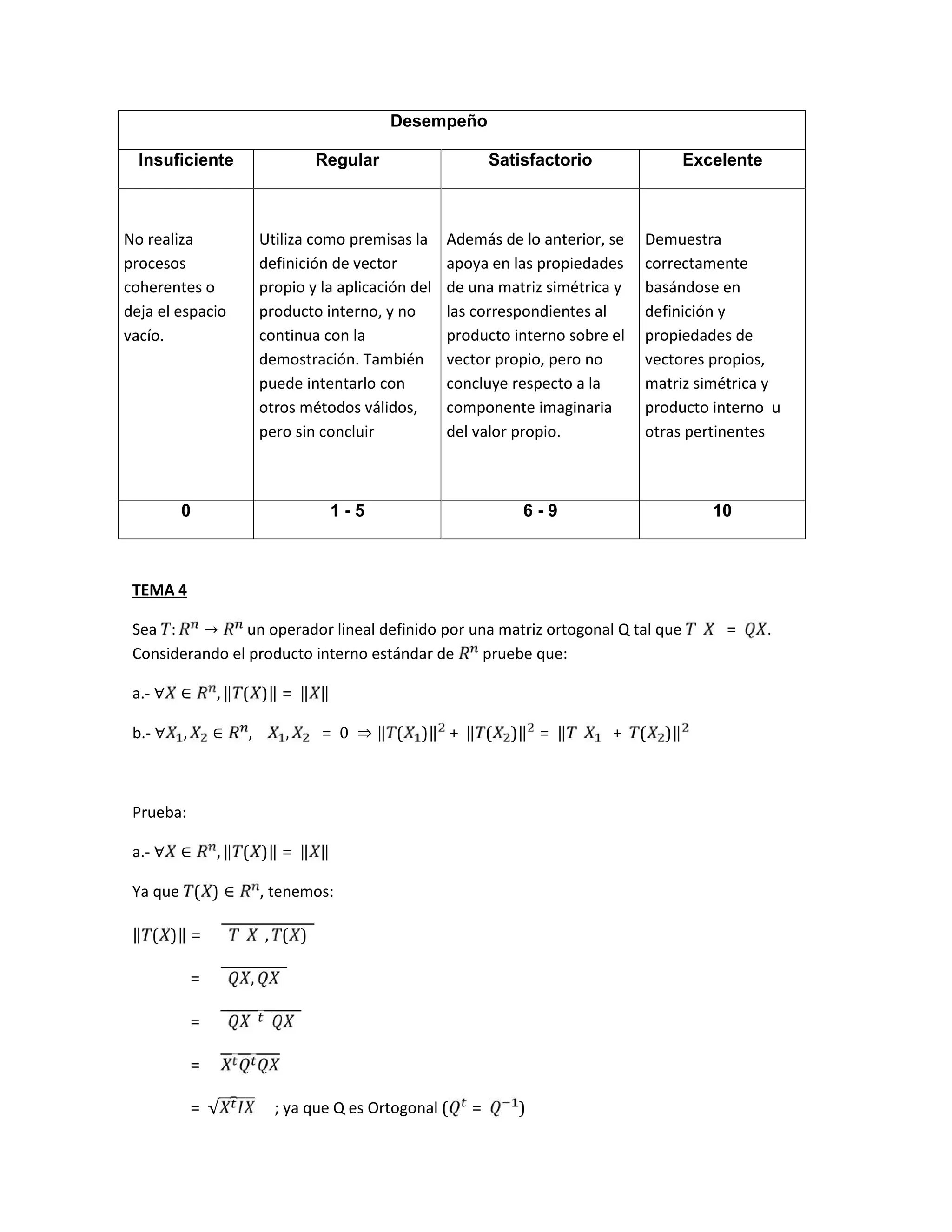
Este documento presenta una evaluación de álgebra lineal que consta de 5 problemas. El primer problema pide construir un operador lineal con ciertas propiedades. El segundo problema define un producto interno y pide calcular una proyección. El tercer problema involucra valores y vectores propios de una matriz. El cuarto problema compara matrices semejantes. El quinto problema pide graficar una cónica dada por una ecuación.

1. ESCUELA SUPERIOR POLITÉCNICA
DEL LITORAL
FACULTAD DE CIENCIAS NATURALES Y
MATEMÁTICAS
DEPARTAMENTO DE MATEMÁTICAS
SEGUNDA EVALUACIÓN DE ÁLGEBRA LINEAL
13 DE FEBRERO DE 2014
TODOS LOS TEMAS TIENEN IGUAL VALOR
1. a. Construya, de ser posible, un operador lineal 2 2 2 2:L M M  tal que:
El espacio propio asociado al valor propio 0  de L sea el espacio
1 2 0 1
Gen ,
0 0 1 0
W
    
     
    
y
0 0 1 2 0 2 0 1
, ,
1 1 0 0 0 0 1 0
L L
       
        
       
Si identifica las imágenes de la base de W como el vector cero: 4 ptos
Si expresa a un vector arbitrario de 2 2M  como combinación lineal de la base
1 2 0 1 0 0 0 2
, , ,
0 0 1 0 1 1 0 0
        
        
        
: 3 ptos
b. Si LA es la matriz asociada a L en una base B de 2 2M  , calcule det ( )LA
2. Sea V un espacio vectorial real, y  1 2 3, ,B v v v una base de V.
a. Demuestre que la función: :V V    dada por:
1 1 2 2 3 3 1 1 2 2 3 3 1 1 2 2 3 32 3a v a v a v b v b v b v a b a b a b      
es un producto interno en V
b. Sea  2 1 3 2Gen - 3 ,H v v v v  y 1 2 32v v v v   . Utilice el producto interno definido en
(a) para calcular H
vproy : 6 ptos

3. 3. Sea
1 0
3 3 3
1 0 2
k
A
 
 
  
 
 
:
a. Determine el valor de k para que 5  sea valor propio de A: 8 ptos
b. Para 20k  determine si A es diagonalizable: 6 ptos
4. Sean A y B dos matrices n n semejantes:
a. Muestre que A y B tienen los mismos valores propios
b. ¿Tienen los mismos vectores propios? Justifique su respuesta:
5. Grafique la cónica dada por la ecuación
5
4 2 2
2
xy x y  

10. ESCUELA SUPERIOR POLITECNICA DEL LITORAL
Instituto de Ciencias Matemáticas
Segunda Evaluación de Álgebra Lineal para Ingeniería en Auditoría y CPA
Guayaquil, 02 de Septiembre de 2010
Nombre:…………………………………………………. Paralelo:………
1.- (20 ptos.) Califique como verdaderas o falsas las siguientes proposiciones.
Justifique su respuesta.
a) El ángulo formado por los vectores y es
b) Si es una transformación lineal tal que ,
entonces
c) Si el conjunto es una base ortonormal de , entonces el conjunto
es base ortogonal de .

11. d) Si , entonces su complemento ortogonal es
e) Sea un operador lineal tal que , entonces T es un
ISOMORFISMO.

12. 2.- (10 ptos.) Sea una transformación lineal tal que:
Determine:
a) El Núcleo de T y su respectiva base.
b) La imagen de T y su respectiva base.

13. 3.- (20 pts.) Sea una transformación lineal tal que:
Determine:
a) La representación matricial de T con respecto a las bases canónicas.
b) La representación matricial de T con respecto a las bases:
,
c) Las matrices que relacionan a las matrices obtenidas en a) y en b).

15. 4.- (10 ptos.) Dada la matriz . Determine:
a) Los valores propios de .
b) Los vectores propios de

16. ESCUELA SUPERIOR POLITECNICA DEL LITORAL
Instituto de Ciencias Matemáticas
Tercera Evaluación de Álgebra Lineal para Ingeniería en Auditoría y CPA
Guayaquil, 16 de Septiembre de 2010
Nombre:…………………………………………………. Paralelo:………
1.- (20 ptos.) Califique como verdaderas o falsas las siguientes proposiciones.
Justifique su respuesta.
a) Sea W un subespacio del espacio vectorial V . Si Ww y R , entonces Ww .
b) La nulidad de la matriz es 1.
c) Existe una transformación lineal tal que y .

17. d) Si es la representación matricial de T con respecto a dos bases
dadas, entonces T es un ISOMORFISMO.
e) Sea V un espacio vectorial real con producto interno. Sean Vvu, dos
vectores ortonormales. Si los vectores vu y vu son ortogonales, entonces

18. 2.- (20 ptos.) Sean y dos bases del espacio
vectorial (Matrices Diagonales 2x2). Sea la matriz cambio de base de a
a) Encuentre los vectores de la base .
b) Usando la matriz de cambio de base , determine si se conoce que
.

19. 3.- (20 pts.) Sea 3RV y 0623/3
zyxR
z
y
x
W un subespacio de V
Determine:
a) El complemento ortogonal de W
b) La proyección de v sobre W si se conoce que
4
1
3
v

20. 4.- (20 ptos.) Sea A la matriz de los coeficientes del sistema lineal:
czyx
bzyx
azyx
32
2
2
a) Determine el espacio fila, el núcleo y el recorrido de A .
b) Si bac 2 , determine si los vectores
c
b
a
u pertenecen a )Im(A .

21. 5.- (20 ptos.) Construya, de ser posible, una transformación lineal que
cumpla con las siguientes condiciones:

22. Escuela Superior Polit´ecnica del Litoral
Instituto de Ciencias Matem´aticas
SOLUCI´ON Y R ´UBRICA
Examen de la Segunda Evaluaci´on de ALGEBRA LINEAL
30 de Agosto de 2012
R´ubrica para todos los temas:
Deficiente
Cuando el estudiante deja vac´ıo, escribe incoherencias o califica
0-1
sin justificar una proposici´on a ser analizada.
Regular
El estudiante demuestra tener una idea de c´omo debe resolver el
2-5
problema o como debe plantearlo, sin embargo tiene serias falencias conceptuales.
Bueno
El estudiante demuestra manejar bien los conceptos o los
6-8
procedimientos pero falta la formalizaci´on o comete errores de c´alculos
Excelente
Tanto el planteamiento como el procedimiento son correctos
9-10
aunque se pueden presentar faltas despreciables.
Ponderaciones:
P1 P2
P3
P4
P5
P6 Total
a b a b
puntos: 10 10 5 5 10 10 10 10 70
1. (10 pts) Demuestre utilizando inducci´on matem´atica el siguiente teorema:
Sea T una transformaci´on lineal del espacio V en el espacio W sobre el campo K, entonces
∀n ∈ N, T
n
i=1
αivi =
n
i=1
αiT(vi)
SOLUCI´ON:
Se probar´a por inducci´on que:
T(v1+v2) = T(v1)+T(v2) ∧ T(αv) = αT(v) ⇒ T(α1v1+. . .+αnvn) = α1T(v1)+. . .+αnT(vn)

23. Para n = 1, se tiene T(α1v1) = α1T(v1) por la primera parte del antecedente de la impli-
caci´on.
Suponemos que el consecuente se cumple para n = k,
⇒ T(α1v1 + . . . + αkvk) = α1T(v1) + . . . + αkT(vk)
Consideremos el caso donde n = k + 1. Por la primera parte del atecedente de la implicaci´on
se tiene,
⇒ T(α1v1 + . . . + αkvk + αk+1vk+1) = T(α1v1 + . . . + αkvk) + T(αk+1vk+1)
Por el supuesto de inducci´on:
T(α1v1 + . . . + αkvk + αk+1vk+1) = α1T(v1) + . . . + αkT(vk) + T(αk+1vk+1)
y por la segunda proposici´on del antecedente de la implicaci´on, se tiene que:
T(α1v1 + . . . + αkvk + αk+1vk+1) = α1T(v1) + . . . + αkT(vk) + αk+1T(vk+1)
2. (10 puntos) Rectifique o ratifique la siguiente DEFINICI´ON:
Definici´on Rectificaci´on ´o Ratificaci´on
Rectificaci´on:
Una matriz A es ortogonal si y
solo si los vectores columnas de Se dice que una matriz inversible A
A son ortogonales. es una matriz ortogonal si A−1
= AT
3. (10 puntos) Califique cada una de las siguientes proposiciones como VERDADERA o FALSA
y justifique formalmente su calificaci´on.
a) La matriz A =
k 0
1 3
es diagonalizable para todo valor real k.
SOLUCI´ON:

24. Se puede observar que los valores propios de la matriz son: k y 3. Realizamos el an´alisis
en el valor k = 3, ya que ser´ıa la situaci´on del valor propio repetido. Para los otros
valores de k, es diagonalizable. Para el valor k = 3, la multiplicidad geom´etrica es 1,
por lo que la matriz no es diagonalizable para k = 3, por lo tanto la proposici´on es
FALSA.
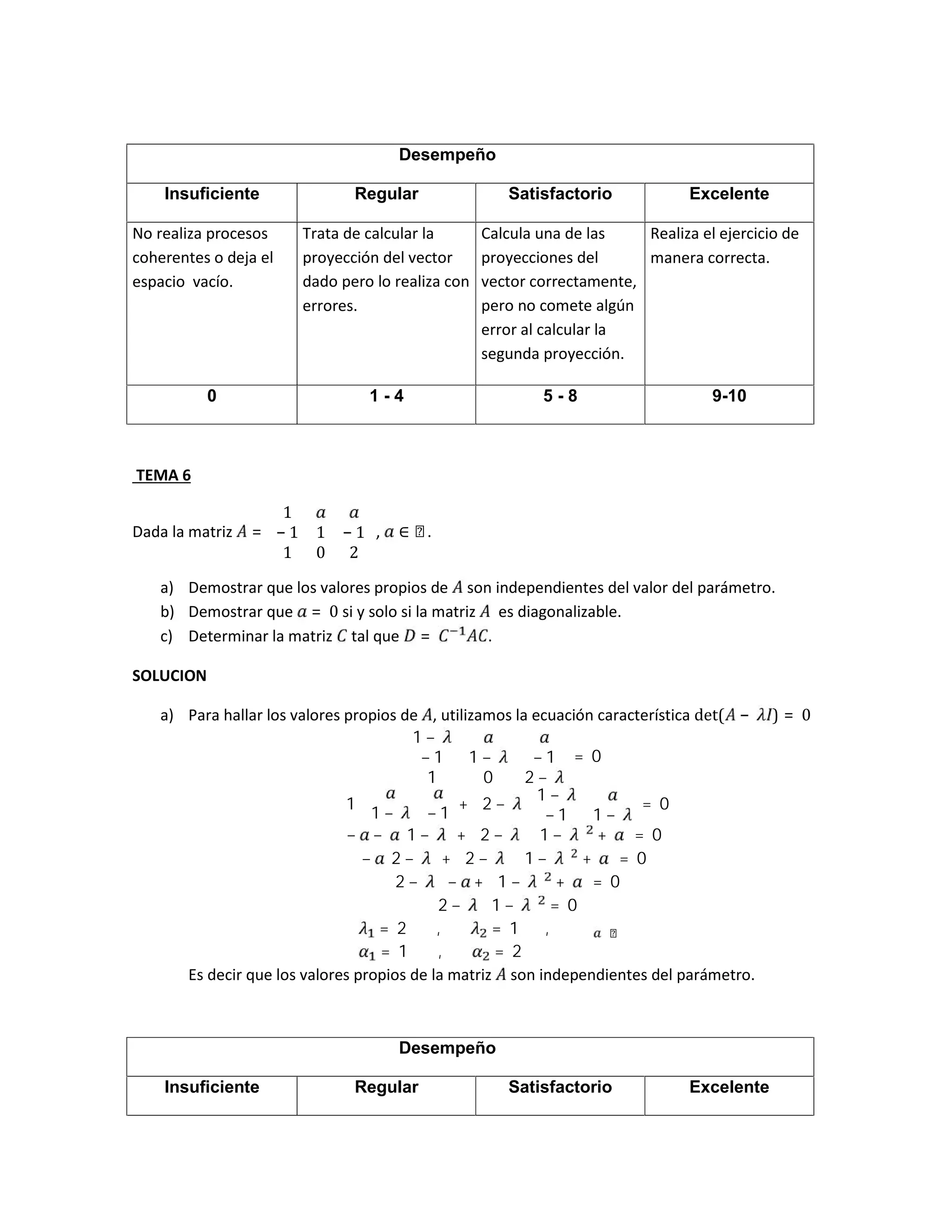
b) La funci´on f : P2 ×P2 → R definida por f(p(x), q(x)) = p(1)q(1) es un producto interno
real.
SOLUCI´ON:
Se deber´ıa cumplir que si p(x) = ax2
+ bx + c, f(p, p) = 0 ⇔ p = 0P2 , pero si a = 0 y
b = −c, se tiene p(x) = −cx + c y entonces f(−cx + c, −cx + c) = (0)(0) = 0. Por lo tanto
la proposici´on es FALSA.
4. (10 puntos) Sea T un operador lineal en R3
definido como:
T


a
b
c

 =


a + b + 2c
b
b + 3c


Determine si T2
es diagonalizable.
SOLUCI´ON:
Sea la matriz de la transformaci´on lineal AT =


1 1 2
0 1 0
0 1 3

, entonces AT2 =


1 4 8
0 1 0
0 4 9


cuyos valores propios son: λ = 1 con multiplicidad algebraica 2 y λ = 9. Haciendo el an´alisis
del valor propio repetido se obtienen los vectores propios {


1
0
0

 ,


0
−2
1

}, por lo tanto es
diagonalizable.
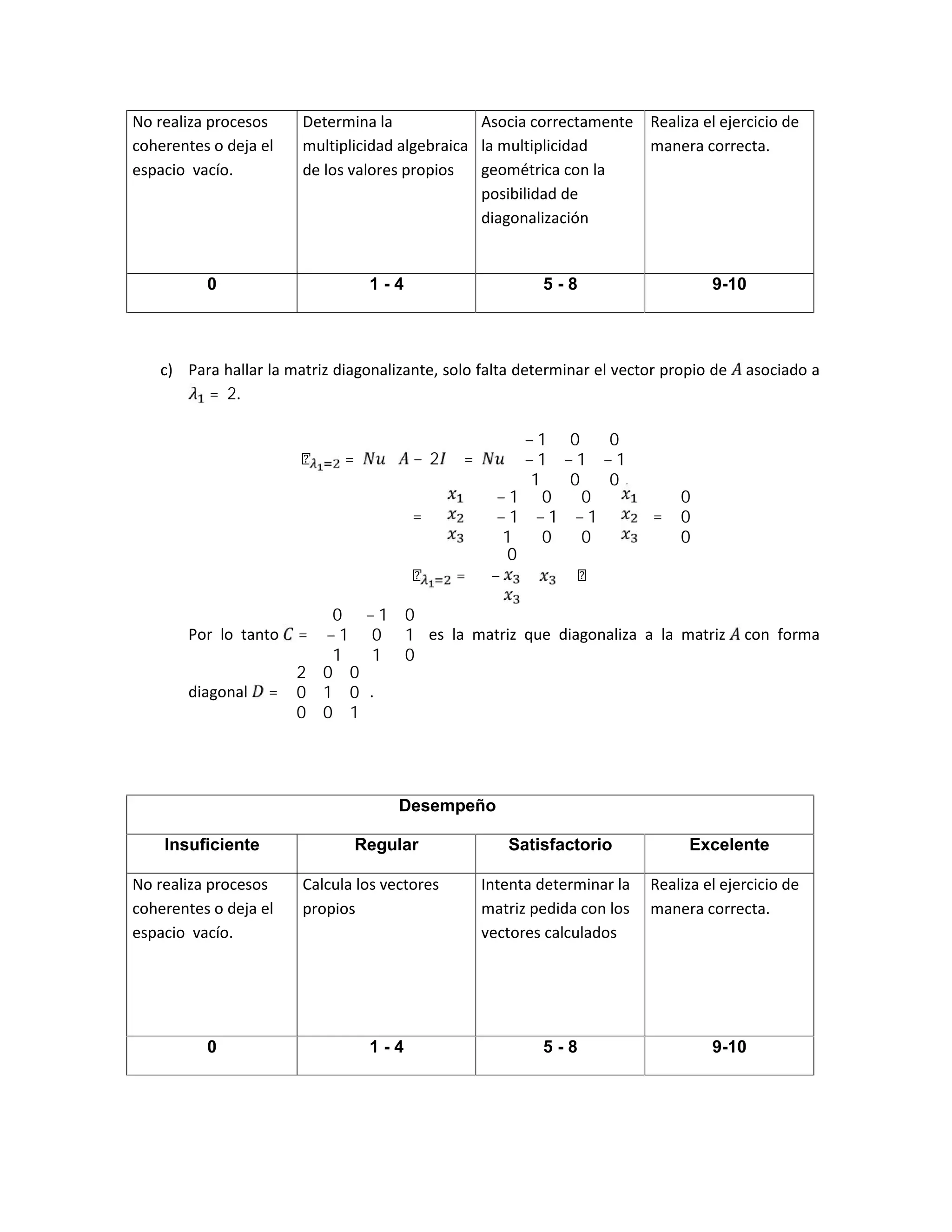
5. (20 puntos) Sea T : V → V un operador lineal definido en V . Sean β1 = {v1, v2, v3} y
β2 = {v1 + 2v2, v2 + v3, v1 − v3} dos bases de V .
a) Si A es la matriz asociada a T con respecto a β1 y B es la matriz asociada a T con
respecto a β2, demuestre que existe una matriz inversible P tal que A = P−1
BP.
SOLUCI´ON:
∀x ∈ V , [T(x)]β1 = A[x]β1 (1)
∀x ∈ V , [T(x)]β2 = B[x]β2 (2)
∀x ∈ V , [x]β2 = P[x]β1 (3)

25. ∀x ∈ V , [T(x)]β2 = P[T(x)]β1 (4)
Reemplazando (4) en (2)
∀x ∈ V , P[T(x)]β1 = B[x]β2 (5)
Reemplazando (1) en (5)
∀x ∈ V , PA[x]β1 = B[x]β2 (6)
Reemplazando (3) en (6)
∀x ∈ V , PA[x]β1 = BP[x]β1 (7)
Por lo que: PA = BP
Dado que P es invertible debido a que es la matriz de transici´on de β1 a β2, se tiene
que A = P−1
BP .
b) A partir de lo anterior, si A =


1 −1 2
0 0 0
1 −2 3

, determine la matriz B.
SOLUCI´ON:
La matriz P−1
es la matriz de transici´on de β2 a β1:
P−1
= ([v1 + 2v2]β1 | [v2 + v3]β1 | [v1 − v3]β1 )
Entonces P−1
=


1 0 1
2 1 0
0 1 −1

 y por lo tanto P =


−1 1 −1
2 −1 2
2 −1 1


Se tiene por el literal anterior que B = PAP−1
, entonces:
B =


−1 1 −1
2 −1 2
2 −1 1




1 −1 2
0 0 0
1 −2 3




1 0 1
2 1 0
0 1 −1

 =


4 −2 3
−8 4 −6
−5 3 −4


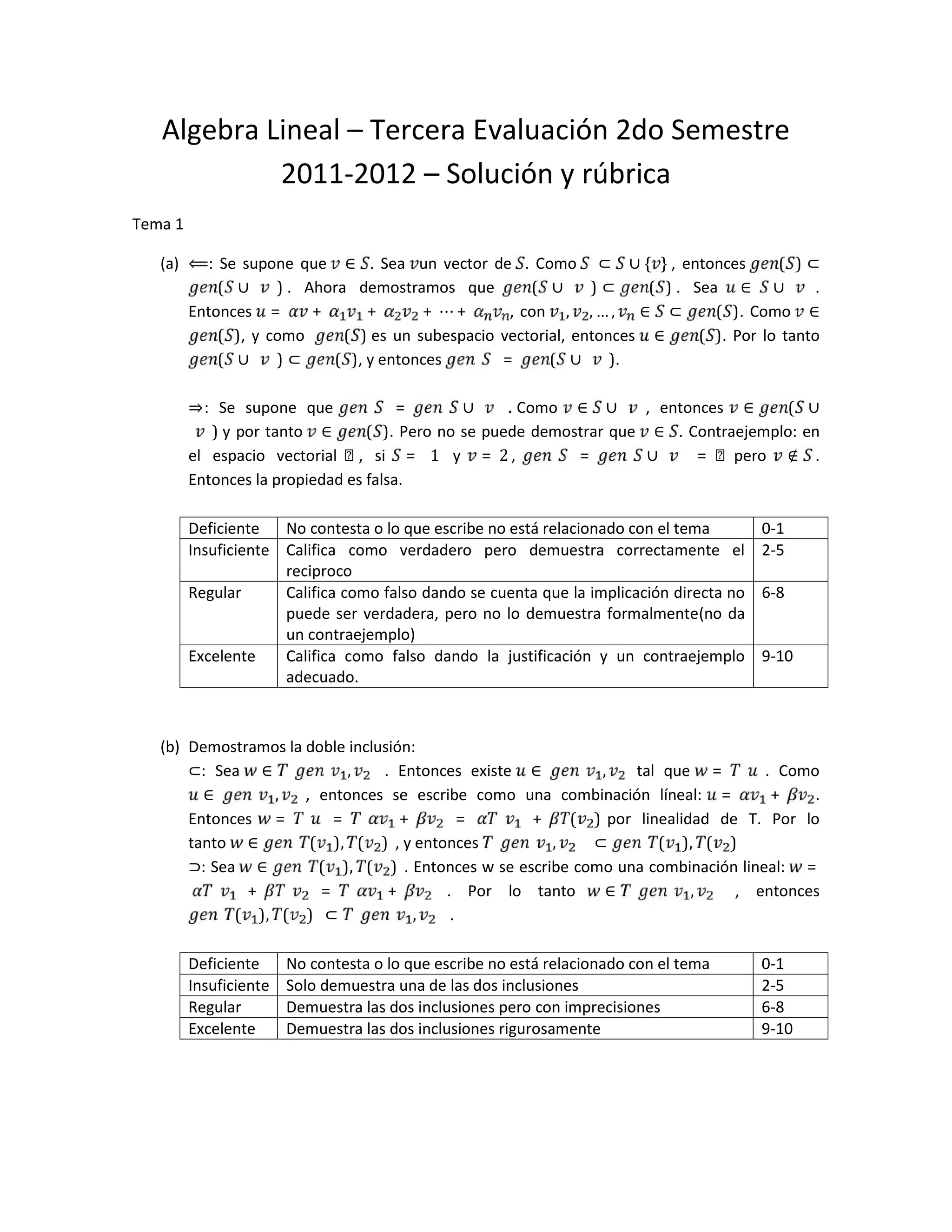
6. (10 puntos) Sea el espacio vectorial V = L(R2
, R2
) y sean T1
x
y
=
x
0
, T2
x
y
=
y
0
,
T3
x
y
=
0
x
, T4
x
y
=
0
y
. Demuestre que {T1, T2, T3, T4} es una base de L.
SOLUCI´ON:
Se probar´a que el conjunto {T1, T2, T3, T4} genera a L y adem´as es linealmente independiente.

26. Toda transformaci´on lineal T : R2
→ R2
puede representarse de la forma:
T
x
y
=
α1 α2
α3 α4
x
y
=
α1x + α2y
α3x + α4y
Se tiene:
α1T1
x
y
+ α2T2
x
y
+ α3T3
x
y
+ α4T4
x
y
= α1
x
0
+ α2
y
0
+ α3
0
x
+ α4
0
y
=
α1x + α2y
α3x + α4y
Se ha probado entonces que gen{T1, T2, T3, T4} = L(R2
, R2
)
Para probar la independencia, la ´unica soluci´on de
α1T1
x
y
+ α2T2
x
y
+ α3T3
x
y
+ α4T4
x
y
= 0L
debe ser α1 = α2 = α3 = α4 = 0, donde 0L es la transformaci´on Cero de L, entonces:
α1
x
0
+ α2
y
0
+ α3
0
x
+ α4
0
y
=
α1x + α2y
α3x + α4y
=
0
0
La ´unica forma que la ecuaci´on anterior se cumpla para todo x y y es que α1 = α2 = α3 =
α4 = 0
Por lo tanto el conjunto {T1, T2, T3, T4} es linealmente independiente.
Otra alternativa de soluci´on:
Sea β1 = β2 = {
1
0
,
0
1
},
[T1]β1β2 = [T1
1
0
]β2 [T1
0
1
]β2 =
1 0
0 0
[T2]β1β2 = [T2
1
0
]β2 [T2
0
1
]β2 =
0 1
0 0
[T3]β1β2 = [T3
1
0
]β2 [T3
0
1
]β2 =
0 0
1 0
[T4]β1β2 = [T4
1
0
]β2 [T4
0
1
]β2 =
0 0
0 1
entonces, el conjunto de matrices {
1 0
0 0
,
0 1
0 0
,
0 0
1 0
,
0 0
0 1
} forman la base can´onica
de M2×2, y como se sabe que la funci´on F : L(R2
, R2
)
T
→
−→
M2×2
F(T)=[T]β1β2
es un isomorfismo del
espacio vectorial L(R2
, R2
) al espacio vectorial M2×2 entonces el conjunto {T1, T2, T3, T4} es
una base de L.

27. Escuela Superior Polit´ecnica del Litoral
Instituto de Ciencias Matem´aticas
Tercera Evaluaci´on de ´ALGEBRA LINEAL
13 de Septiembre de 2012
Nombre: Paralelo: Firma:
1. (10 pts) Defina Espacio Vectorial sobre el campo K.
2. (10 puntos) Sea V = C[0, 1] y H = {f ∈ V | f2
(0) = f2
(1)}. Determine si H es un subespa-
cio de V .

28. 3. (10 puntos)Sea T : R3
→ R3
la trasformaci´on lineal definida por:
T


x
y
z

 =


x − 2y + z
y + z
x − y + 3z


Detemine si T y T2
son isomorfismos.

29. 4. (10 puntos) Construya de ser posible, una Transformaci´on Lineal de R2
en R2
que transforme
todo vector de R2
en un vector que pertenezca a la recta y = 2x.

30. 5. (10 puntos) Sea V = C[0, 1] y f, g ∈ V . Demuestre que si el conjunto {f, g} es linealmente
dependiente entonces:
W =
f(x) g(x)
f′
(x) g′
(x)
= 0
6. (10 puntos) Sean A y B matrices cuadradas. Demuestre que si A es semejante a B, entonces
B es semejante a A.

31. 7. (10 puntos) Dada la matriz A =


1 10 1
2 2 2
−1 −8 k

, determine los valores de k para que la
nulidad de A sea cero.
8. (10 puntos) Sean u, v1, v2, . . . , vn vectores pertenecientes al espacio euclidiano V . Demuestre
que si u es ortogonal a v1, v2, . . . , vn, entonces u es ortogonal a todo vector de gen{v1, v2, . . . , vn}

32. 9. (10 puntos) Sean u =


2
5
0

 y v =


3
−1
1

 dos vectores del espacio euclidiano R3
. Exprese al
vector u como la suma de dos vectores p y q tal que p es paralelo a v y q es ortogonal a v.

33. 10. (10 puntos) Grafique la curva descrita por la ecuaci´on x2
+ 2xy + y2
− 4
√
2x − 2 = 0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5
-4
-3
-2
-1
0
1
2
3
4
5

40. ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL
INSTITUTO DE CIENCIAS MATEMÁTICAS
SEGUNDA EVALUACIÓN DE ÁLGEBRA LINEAL
Nombre: ………………………………. Paralelo: ……
Firma: ……………………….. 2 de septiembre de 2010
1. (20 ptos) Califique como verdaderas o falsas las siguientes proposiciones. Justifique
su respuesta.
a. Sea :T V W una transformación lineal, Sea S un subespacio vectorial de V, entonces
( ) ( ),T S w W w T v v S es subespacio de W.
b. Existe un espacio vectorial V y existe un operador lineal :L V V tal que
Nu( ) Im( )L L
c. En 2P se define el producto interno
, 1 1 0 0 1 1p x q x p q p q p q , entonces 2
1 1x x
d. Si A y B son matrices semejantes, entonces t
A y t
B también lo son.

41. 2. (20 ptos) Sea 3
2:T P  tal que
( 1)
( ) (0)
(1)
p
T p x p
p
.
a. Determine el núcleo e imagen de T y sus respectivas bases.
b. Si T es invertible, calcule 1
T

42. 3. (25 ptos) Sea
2 3
V M , con el producto interno , Traza( )tA B AB .
Sea 0
a b c
W V a b c d e f
d e f
a. Determine el complemento ortogonal de W.
b. Sea
1 0 1
0 2 0
C V , calcule la proyección ortogonal de C sobre W
Obs.-La traza de una matriz cuadrada es la suma de los elementos de la diagonal principal.

43. 4. (20 ptos) Sea L una transformación lineal de 2P en 2 2S tal que:
2 21 0 0 0 1 0
1 , 1 , 1
0 1 0 1 0 2
L x L x L x
a. Determine la regla de correspondencia de L.
b. Encuentre la matriz asociada a L en las bases:
2 2
1 1, 1, 1B x x x , 2
1 0 1 0 0 1
, ,
0 1 0 1 1 0
B

44. 5. (15 ptos) Grafique el lugar geométrico correspondiente a 2 2
9 6 10x xy y

45. ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL
INSTITUTO DE CIENCIAS MATEMÁTICAS
TERCERA EVALUACIÓN DE ÁLGEBRA LINEAL
Nombre: ………………………………. Paralelo: ……
Firma: ……………………….. 16 de septiembre de 2010
1. (20 ptos) Califique como verdaderas o falsas las siguientes proposiciones. Justifique
su respuesta.
a. Existe una transformación lineal : n
nT P tal que 0Nu 0 ,VT v , donde
0 0, 0V
n
v v .
b. Si 1 1,..., nB v v es base de V y L una transformación lineal de V en W, entonces
2 1 ,..., nB L v L v genera a W.
c. Si A es una matriz invertible y es valor propio de A, entonces es diferente de cero.
d. Dos matrices semejantes tienen los mismos valores y vectores propios.

46. 2. ( 20 ptos) Sea f un producto interno real en el espacio vectorial 1P , tal que 21 ,
1x y 11 x,f .
a. Encuentre la regla de correspondencia de f
b. Sea 1 1 0/W p x P p un subespacio vectorial de 1P , encuentre una base y
determine la dimensión de W
c. Construya una base para 1P formada por un vector de W y por un vector de W

47. 3. (20 ptos) Sea 2
1:L P una transformación lineal tal que la matriz
52
31
A es la
representación matricial de L respecto de las bases 1
1 2
,
1 1
B de 2
 y
2 1 , 1 3B x x de 1P .
a. Determine una base y la dimensión del núcleo y recorrido de L
b. ¿Es L invertible? Justifique su respuesta

48. 4. (20 ptos) a. Encuentre una matriz 22xMA , tal que 11 y 32 sean sus
valores propios, y, además:
1
1
Gen
1
E
2
5
Gen
1
E
b. Sea 11 PP:L un operador lineal tal que A es su representación matricial respecto
de la base 1 1 , 1B x x de 1P . Encuentre, de ser posible, una base 2B de 1P
respecto de la cual la matriz asociada a L sea una matriz diagonal.

49. 5. (20 ptos) Sea el espacio vectorial 4
V  . Sean los subespacios de V :
4
/ 0 , 2 0
a
b
H a b c a b c d
c
d
 ,
4 -1
1 0
Gen ,
1 -1
3 2
W
Encuentre una base y determine la dimensión de los subespacios de V :
a. WH
b. WH

56. Ramiro J. Saltos
Instituto de Ciencias Matemáticas
Algebra Lineal: Solución de la Segunda Evaluación
1. (20 puntos) Califique como verdaderas o falsas a las siguientes proposiciones. Justifique
formalmente sus repuestas.
a) Una transformación lineal cuyo núcleo es  VO , es invertible
Sea 32
: RRT  una transformación lineal definida por

















ba
b
a
b
a
T
Si obtenemos su núcleo fácilmente nos damos cuenta que es 





0
0
pero como la WV dimdim  , T no es
invertible.
También es válido decir que el hecho que la transformación lineal sea inyectiva no necesariamente debe ser
sobreyectiva
Falso
b) :, Rtr  







)()(
)()(
trSentCos
tCostrSen
A es ortogonal
Para que la matriz sea ortogonal, el producto interno entre sus columnas debe ser igual a 0 y al mismo
tiempo el producto interno de cada columna consigo misma debe ser igual a 1. Entonces, utilizando el
producto interno canónico:
00
0)()()()(
0
)(
)(
)(
)(






















tCostrSentCostrSen
trSen
tCos
tCos
trSen
  01)(
1)(1)(
1)()(
1
)(
)(
)(
)(
22
222
222























rtSen
tSentSenr
tCostSenr
tCos
trSen
tCos
trSen
20
0)(
0)(2



tt
tSen
tSen
1
1
01
2
2



r
r
r
Por lo tanto la igualdad sólo se cumple para los valores de r y t encontrados y no para todos los reales. Se
igual procedimiento para la segunda columna
Falso

57. Ramiro J. Saltos
c) Sea V un espacio vectorial real con producto interno. Sean Vvu , dos vectores ortonormales.
Si los vectores vu   y vu   son ortogonales, entonces  
0)/()/()/()/(
0)/()/()/()/(
0)/(
22



vvvuvuuu
vvuvvuuu
vuvu



Pero como los vectores u y v son ortonormales, sabemos que: 1)/()/(  vvuu








22
22
22
0
0)/()/( vvuu
Verdadero
d) Si  es un valor propio de 







10
01
A , entonces   AAA 
21
 
Primero tenemos que darnos cuenta la matriz A es ortogonal, eso se ve fácilmente porque el producto
interno entre sus columnas es cero y al mismo tiempo el producto interno de cada columna consigo misma es
uno, entonces:
AAAA T
  11
También como A es una matriz diagonal sus valores propios son los elementos de la diagonal principal, es
decir:
1
1




Finalmente:
 
 
AA
AAA
AAA
22
2
2
11
1


  
 
 
AA
AA
AA
AAA
AAA
2
1
2
1
2
1
)()2(
2
1
)2(
2
2
11
1
11
1








 
Verdadero

58. Ramiro J. Saltos
2. (15 puntos) Sea 2
22: RML x  una transformación lineal tal que:
























1
1
01
01
10
01
01
10
LLL y 











0
0
00
01
L
Determine:
a) )Im(),( LLNu
b) La matriz asociada a L respecto a las bases canónicas de cada espacio
La mejor opción es encontrar la regla de correspondencia de L , y para ello necesitamos una base del espacio
de partida y para armarla usamos los cuatro vectores que nos dan de datos, así:































00
01
,
01
01
,
10
01
,
01
10
B
Y al vector típico de 22xM lo escribimos como combinación lineal de los vectores de esta base, luego
planteamos el sistema de ecuaciones y obtenemos los escalares en términos de dcba ,,,






























00
01
01
01
10
01
01
10
4321 
dc
ba














231
1432


dc
ba











2
31
1
432




d
c
b
a
bc
bc


3
3


dcba
bcda


4
4


Finalmente reemplazamos los datos en la combinación lineal inicial:






























00
01
01
01
10
01
01
10
4321 TTTT
dc
ba
T 






























0
0
)(
1
1
)(
1
1
)(
1
1
)( dcbabcdb
dc
ba
T














dc
dc
dc
ba
T
Calculando el núcleo tenemos:





0
0
dc
dc












000
011
011
011

dc
dc

 0












 0/)( 22 dcM
dc
ba
LNu x

59. Ramiro J. Saltos
Y la imagen:





ydc
xdc













xy
x
y
x
00
11
11
11

yx
xy

 0












 yxR
y
x
L /)Im( 2
Para obtener la matriz asociada a la base canónica, sabemos que:































10
00
,
01
00
,
00
10
,
00
01
22 xMCB



















1
0
,
0
1
2
CR
B












0
0
00
01
T 











0
0
00
10
T 











1
1
01
00
T 











1
1
10
00
T

































































2222
10
00
01
00
00
10
00
01
CRCRCRCR
BBBB
TTTTA







1100
1100
A

60. Ramiro J. Saltos
3. (15 puntos) Sea











a
a
a
A
11
11
11
Determine:
a) Los valores propios de A
b) Una base para cada espacio propio de A


















a
a
a
IA
11
11
11
     
 
02)(3)(
0)(11)(1)()(
0)(111)(11)()(
3
2
2






aa
aaaa
aaaa
Ahora realizamos un cambio de variable para visualizar mejor las cosas:
 ax
0233
 xx
Aplicando división sintética:
0211
211
23011



0)1)(2)(1(
0)2)(1( 2


xxx
xxx
1
1
1



a
a
x


2
2
2



a
a
x


Y finalmente hallamos cada espacio propio reemplazando cada  en la matriz IA 
1aE





















000
000
111
111
111
111
cba
cba

 0































 











1
0
1
0
1
1
cb
c
b
cb
c
b
a































1
0
1
,
0
1
1
EB
2aE



















































101
110
000
211
110
000
211
330
330
211
121
112
cb
cb

 0
ca
ca

 0
































1
1
1
c
c
c
c
c
b
a





















1
1
1
EB

61. Ramiro J. Saltos
4. (5 puntos) Determine si la matriz











101
110
101
A es diagonalizable


















101
110
101
IA
Calculamos la ecuación característica:
 
  01)1()1(
0)1()1()1(
2
2




1
0)1(




0)2)((
0)11)(11(
01)1( 2






0
2
02




Debemos recordar el corolario que dice: “Si nxnMA tiene n valores propios distintos, entonces A es
diagonalizable”
Como tenemos tres valores propios distintos, entonces A es diagonalizable

62. Ramiro J. Saltos
5. (15 puntos) Sea 3RV  y





















 0623/3
zyxR
z
y
x
W un subespacio de V
Determine:
a) El complemento ortogonal de W
b) La proyección de v sobre W si se conoce que











4
1
3
v
Para calcular el complemente primero necesitamos una base de W
zxy
zyx
632
0623
























































2
6
0
0
3
2
2
63
2
2
2
2
zx
z
zx
x
z
y
x
z
y
x































1
3
0
,
0
3
2
WB
Sea 











W
c
b
a
ba
ba
c
b
a
32
032
0
0
3
2

































bc
cb
c
b
a
3
03
0
1
3
0






















































 
0332/3
bcbaR
c
b
a
W
Para hallar la proyección del vector que nos piden es mejor calcularla sobre 
W debido a que la base de este
subespacio tiene un solo vector y ortonormalizarla será más sencillo.















































6
2
3
6
2
3
2
2
2
b
b
b
b
c
b
a
c
b
a






















 
6
2
3
W
B

63. Ramiro J. Saltos
Ahora procedemos a ortonormalizar esta base:
1
1
1
1
v
v
u 
 
749
3649
6
2
3
6
2
3
/
1
1
1
111






































v
v
v
vvv






















 
6
2
3
7
1*
WB
Vamos a suponer que v se puede escribir como la suma de dos vectores Wh  y 
Wp , hallaremos p y
luego contestaremos la pregunta al encontrar pvh 
  11
Pr
uuvp
voyp W

 
 
























































































6
2
3
49
13
6
2
3
2429
49
1
6
2
3
6
2
3
4
1
3
49
1
p
p
p





































49
248
49
75
49
186
49
52
49
26
49
39
4
1
3
h
h













49
248
49
75
49
186
Pr voyW

64. Instituto de Ciencias Matemáticas
Algebra Lineal: Solución de la Primera Evaluación
Tema 1: (20 puntos) Califique como verdaderas o falsas las siguientes proposiciones. Justifique
formalmente su respuesta
a) Si la matriz B se obtiene a partir de la matriz A por medio de un intercambio de filas, entonces
)()( BA   (Verdadero)
Por definición, la matriz A es equivalente por renglones a la matriz B si A puede reducirse a B mediante
operaciones elementales de renglón
En este caso la matriz B se obtiene por un simple intercambio de las filas (renglones) de A , entonces
BA RR  dado que los renglones de A y B son los mismos excepto que están escritos en un orden diferente
También hay que recordar que )dim()dim()())dim(Im( AA RCAA  
)()( BA  
b) Si 53xMA es una matriz cualquiera, entonces 3)( Av (Falso)
Sea 53
00100
00010
11001
xMA 









 
 . Sea )(ANu
e
d
c
b
a
X 





















































 

0
0
0
00100
00010
11001
3
e
d
c
b
a
OAX R










 
000100
000010
011001
De donde obtenemos:
eda
eda

 0
0b 0c

















































 

















1
0
0
0
1
0
1
0
0
1
0
0
ed
e
d
ed
e
d
c
b
a

















































1
0
0
0
1
,
0
1
0
0
1
)( ANuB 2)(  Av

65. c) Sea V un espacio vectorial. Sea VBA , , entonces )()()( BgenAgenBAgen  (Falso)
Sea 3
RV  . Sea









































1
0
0
,
0
1
0
,
0
0
1
A y VB 































2
0
0
,
0
1
0






















0
1
0
BA





















 0/)( 3
caR
c
b
a
BAgen






















 RcbaR
c
b
a
Agen ,,/)( 3
y





















 0/)( 3
aR
c
b
a
Bgen






















 RcbaR
c
b
a
BgenAgen ,0/)()( 3
)()()( BgenAgenBAgen 
d) Sea W un subespacio del espacio vectorial V . Si Ww y R , entonces Ww (Falso)
Sea 2
RV  . Sea












 0/2
aR
b
a
W un subespacio de V . Sea 0
Sea 






0
1
w , este vector no pertenece a W por no cumplir la condición de que 0a
  












0
0
0
1
0w
Por hipótesis sabemos que W es un subespacio y por tanto contiene al nulo de V y VOw 
Ww
e) Si RRL : es una transformación lineal, entonces   )()( 22
vLvL  (Falso)
Sea aaL 2)(  una transformación lineal
Sea 2a
 
 
816
)4(4
)2()2(
2
22



L
LL
  )()( 22
vLvL 

66. Tema 2: (10 puntos) Sea












 00/ yx
y
x
V con las operaciones:




















21
21
2
2
1
1
4
9
yy
xx
y
x
y
x














 


y
x
y
x
2
2
2
3
Si  ,,V es un espacio vectorial, determine:
a) El neutro o cero vectorial de V
b) Si Vv  , el inverso aditivo de v
Este ejercicio se presenta bastante confuso, debido a que la manera en que es planteado da a entender que
primero hay que determinar si V es un espacio vectorial. Pero no vamos a analizar la validez del ejercicio
planteado, sino que vamos a resolver lo que nos piden en cada literal.
a)
 Usando el teorema Vv  VOv 0























1
1
2
3
0
0)0(2
0)0(2
V
V
V
O
y
x
O
y
x
O
 Usando el axioma VOV  Vv  vOv V 
Sea V
b
a
v 





 . Sea 






y
x
OV






























b
a
by
ax
b
a
y
x
b
a
4
9 9
1
9


x
aax
4
1
4


y
bby









4
1
9
1
VO
El nulo pertenece a V porque sus componentes son mayores que 0
Hay que notar que usando las dos formas de resolución no nos queda el mismo nulo, pero esto se debe al
mal planteamiento del problema. Utilizando ambas alternativas siempre debe quedar la misma respuesta

67. b)
 Usando el teorema Vv  '1 vv 



























y
xv
y
x
v
y
x
v
4
1
9
1
'
2
3
'
1'
1)1(2
1)1(2
 Usando el axioma Vv  Vv  ' VOvv  '
La pregunta aquí es con cuál nulo trabajamos. Para este caso debemos usar el obtenido al usar el axioma
porque estamos calculando el inverso de la misma manera que ese neutro
Sea V
y
x
v 





 . Sea 






b
a
v'


































4
1
9
1
4
9
4
1
9
1
yb
xa
b
a
y
x
x
a
xa
81
1
9
19


y
b
yb
16
1
4
14











y
xv
16
1
81
1
'
Ambos inversos pertenecen a V por ser sus componentes mayores que 0
Con el mismo argumento mencionado al calcular el VO sabemos que nos debió quedar la misma respuesta.
También se puede notar que V no es un espacio vectorial por no cumplirse el siguiente axioma:
M10) Vv  vv 1
Sea V
y
x
v 













































y
x
y
x
y
x
y
x
y
x
y
x
4
9
2
3
1
1)1(2
1)1(2

68. Tema 3: (20 puntos) Sea 23xMV  . Sean 1W el conjunto de las matrices que tienen la primera y
última fila iguales; 2W el conjunto de las matrices que tienen la primera columna igual a su
segunda columna; y 3W el conjunto de las matrices 23xA tal que 12  iai , .3,2,1i
Determine.
a) Los conjuntos que son subespacios de V
b) La intersección entre los subespacios encontrados en el literal anterior
c) La suma entre los subespacios encontrados en el primer literal
d) Una base para el subespacio intersección y otra para el subespacio suma, obtenidos en (b)
y (c), respectivamente.
Para hallar 1W hay que tener en cuenta que su primera y última fila son iguales, por tanto las componentes
en dichas filas deben ser correspondientemente iguales, así nos queda que:





















 fbeaM
fe
dc
ba
W x /231
Ahora procedemos a determinar si 1W es un subespacio de V
1) 1, Wwv  1Wwv 
Sea











11
11
11
fe
dc
ba
v y 1
22
22
22
W
fe
dc
ba
w 











Como ambos vectores pertenecen a 1W cumplen con la condición del mismo, con lo que tenemos que:
11 ea  11 fb  22 ea  22 fb 














2121
2121
2121
ffee
ddcc
bbaa
wv
Ahora hay que ver si la suma de ambos cumple la condición
00
2121
2121



eeee
eeaa
00
2121
2121



ffff
ffbb
Por tanto 1Wwv 
2) R 1Wv  1Wv 
Sean R . Sea 1W
fe
dc
ba
v 











Sabemos que ea  y fb  entonces 0 ea y 0 fb

69. 










fe
dc
ba
v




00
0)0(
0)(
0







ea
ea
00
0)0(
0)(
0







fb
fb
Por tanto 1Wv 
1W es un subespacio de V
El mismo procedimiento vamos a realizar con 2W pero aquí hay que notar que ambas columnas son
iguales, por tanto las componentes en dichas columnas deben ser correspondientemente iguales, así nos
queda que:





















 fedcbaM
fe
dc
ba
W x /232
Ahora procedemos a determinar si 2W es un subespacio de V
1) 2, Wwv  2Wwv 
Sea











11
11
11
fe
dc
ba
v y 2
22
22
22
W
fe
dc
ba
w 











Como ambos vectores pertenecen a 2W cumplen con la condición del mismo, con lo que tenemos que:
011
11


ba
ba
011
11


dc
dc
011
11


fe
fe
022
22


ba
ba
022
22


dc
dc
022
22


fe
fe














2121
2121
2121
ffee
ddcc
bbaa
wv
00
000
0)()(
0)()(
2211
2121




baba
bbaa
00
000
0)()(
0)()(
2211
2121




dcdc
ddcc
00
000
0)()(
0)()(
2211
2121




fefe
ffee
Por tanto 2Wwv 
2) R 2Wv  2Wv 
Sean R . Sea 2W
fe
dc
ba
v 












70. 










fe
dc
ba
v




00
0)0(
0)(
0







ba
ba
00
0)0(
0)(
0







dc
dc
00
0)0(
0)(
0







fe
fe
Por tanto 2Wv 
2W es un subespacio de V
Finalmente nos falta encontrar 3W y determinar si este es un subespacio, y para ello hay que utilizar la
regla de correspondencia para determinar el valor de las componentes en la segunda columna, la cual es
12  iai
0
11
12
12


a
a
1
12
22
22


a
a
2
13
32
32


a
a





















 RcbaM
c
b
a
W x ,,/
2
1
0
233
Para determinar si 3W es un subespacio hay que recordar que todo subespacio debe contener a vector nulo
del espacio vectorial, pero en este caso el nulo que es










00
00
00
no pertenece a 3W por no cumplir con la
forma de todo vector de 3W , la cual consiste en que su segunda columna siempre tendrá 0 , 1 y 2 ,
respectivamente
3W no es un subespacio de V
Procederemos a encontrar la intersección entre los subespacios hallados y una base para la misma. Sabemos
que:






















 00/231 fbeaM
fe
dc
ba
W x






















 000/232 fedcbaM
fe
dc
ba
W x
Por tanto:





















 0/2321 fedcbafbeaM
fe
dc
ba
WW x

71. Pero no es correcto dejar expresada la intersección en función de muchas condiciones. A estas hay que
simplificarlas usando Gauss, así:













0
0
0
0
0
fe
dc
ba
fb
ea
)1(
0110000
0001100
0010010
0100010
0010001
)1(
0110000
0001100
0000011
0100010
0010001
2313 AA





















































































0000000
0001100
0110000
0100010
0010001
)1(
0110000
0001100
0110000
0100010
0010001
35A
Como ya no podemos seguir obteniendo más filas llenas de ceros, entonces la intersección sólo quedará en
función de estas condiciones:





















 0/2321 dcfefbeaM
fe
dc
ba
WW x
Para obtener una base para la intersección debemos reemplazar las condiciones en el vector típico de la
misma, pero antes hay que hacer unos cuantos despejes para dejar al vector en función de la menor
cantidad posible de variables
ea
ea

 0
ef
fe

 0
eb
fb
fb


 0
dc
dc

 0
Sea 21 WW
fe
dc
ba






















































00
11
00
11
00
11
de
ee
dd
ee
fe
dc
ba






























 
00
11
00
,
11
00
11
21 WWB 2dim 21 WW
Finalmente hallaremos las condiciones del subespacio suma y una base para el mismo, pero antes
necesitamos las bases de los subespacios 1W y 2W

72. Para 1W
Sea 1W
fe
dc
ba












































































00
10
00
00
01
00
10
00
10
01
00
01
dcba
ba
dc
ba
fe
dc
ba



















































00
10
00
,
00
01
00
,
10
00
10
,
01
00
01
1WB 4dim 1 W
Para 2W
Sea 2W
fe
dc
ba

































































11
00
00
00
11
00
00
00
11
eca
ee
cc
aa
fe
dc
ba









































11
00
00
,
00
11
00
,
00
00
11
2WB 3dim 2 W
Una vez obtenidas las bases, podemos calcular cuál va a ser la dimensión de 21 WW  para saber cuántos
vectores deberán estar en su base. Sabemos que:
       
 
  5dim
234dim
dimdimdimdim
21
21
212121



WW
WW
WWWWWW
Por tanto habrá 5 vectores en la base
 


















































































11
00
00
,
00
11
00
,
00
00
11
,
00
10
00
,
00
01
00
,
10
00
10
,
01
00
01
21
21 21
genWW
BBgenWW WW
Pero el conjunto generador tiene 7 vectores, eso significa que hay dos vectores de más, los cuales
eliminaremos colocando los vectores de este conjunto en una matriz donde cada fila representa un vector y
luego simplificamos hasta obtener la mayor cantidad posible de filas llenas de ceros

73. 





































































110000
000000
000000
001000
000100
100010
010001
)1(
)1(
110000
000000
010010
001000
000100
100010
010001
)1(
)1(
)1(
110000
001100
000011
001000
000100
100010
010001
75
25
46
36
15
A
A
A
A
A
Lo que significa que los vectores 5 y 6 dependen de los otros




























































 
11
00
00
,
00
10
00
,
00
01
00
,
10
00
10
,
01
00
01
21 WWB
Ahora sólo falta hallar las condiciones del subespacio suma y para ello escribimos al vector típico como
combinación lineal de los vectores de la base y simplificamos el sistema hasta obtener las condiciones, así:
Sea 21 WW
fe
dc
ba
























































































5251
43
21
54321
11
00
00
00
10
00
00
01
00
10
00
10
01
00
01




fe
dc
ba



































































eabf
ae
d
c
b
a
A
bf
ae
d
c
b
a
A
A
f
e
d
c
b
a
00000
10000
01000
00100
00010
00001
)1(
10000
10000
01000
00100
00010
00001
)1(
)1(
10010
10001
01000
00100
00010
00001
56
26
15





















 0/2321 eabfM
fe
dc
ba
WW x

74. Tema 4: (10 puntos) Sea V un espacio vectorial y  321 ,, vvvB  una base de V . Se define el
conjunto:
 3132121 3,3,2 vvvvvvvgenW 
a) Determine una base para W , denotada como WB
b) Si es factible, calcule la matriz de cambio de base de B a WB
Siempre es recomendable primero leer bien el planteamiento del problema junto con lo que solicitan hallar.
Razonando un poco, en el literal “b” nos piden calcular una matriz de cambio de base y para poder hacerlo
la base WB debe tener exactamente 3 vectores al igual que la base B de V
Si esto sucede significaría que la base de W es también una base para V , por tanto VW  . Así que para
que sea factible resolver el literal “b” habrá que demostrar que el conjunto generador de W es una base
para V
Para ello partimos de la hipótesis que nos dice que los vectores  321 ,, vvv son linealmente independientes
por ser una base para V , esto implicaría que:
0321332211   VOvvv
Lo cual se cumple por ser linealmente independientes
Para demostrar que los vectores del conjunto generador de W son linealmente independientes los
escribimos como combinación lineal y los igualamos al VO
     
      V
V
Ovccvccvccc
Ovvcvvvcvvc


3322211321
3133212211
332
332
Con lo que hemos obtenido una ecuación parecida a la primera expresada en términos de  321 ,, vvv , y por
hipótesis los escalares que los multiplican deben ser iguales a cero, con lo que planteamos un sistema de
ecuaciones y procedemos a calcular los valores de los escales ic








03
032
0
32
21
321
cc
cc
ccc
)1(
)1(
0310
01010
0111
)4(
0310
0250
0111
)2(
0310
0032
0111
22
21
3212
A
A
AA












































































0100
0010
0001
)10(
)11(
0100
01010
01101
13
1
01300
01010
01101
32
31
3
A
A
M 0321  ccc
Si nos hubiese quedado al resolver el sistema una o más filas con ceros, el sistema tenía infinita soluciones
y en ese caso los vectores del conjunto generador de W serían linealmente dependientes
 3132121 3;3;2 vvvvvvvBW 

75. Para hallar la matriz que nos piden vamos a suponer que  321 ,, uuuBW  tal que:
211 2vvu  3212 3 vvvu  313 3vvu 
También recordamos que:
     












 BBBBB uuuC W 221
 











0
2
1
1 B
u  













1
3
1
2 B
u  











3
0
1
3 B
u













310
032
111
BBW
C
Y para hallar la matriz de cambio que nos piden habrá que sacar la inversa de la matriz arriba encontrada
)1(
)1(
100310
4121010
001111
)4(
100310
012250
001111
)2(
100310
010032
001111
23
21
3212
A
A
AA






























































































13
5
13
1
13
2
100
13
2
13
3
13
6
010
13
3
13
2
13
9
001
)10(
)11(
13
5
13
1
13
2
100
4121010
4111101
13
1
5121300
4121010
4111101
32
31
3
A
A
M















 
13
5
13
1
13
2
13
2
13
3
13
6
13
3
13
2
13
9
WBBC

76. Tema 5: (10 puntos) Sea A la matriz de los coeficientes del sistema lineal:
czyx
bzyx
azyx



32
2
2
a) Determine el espacio fila, el núcleo y el recorrido de A
b) Si bac  2 , determine si el vector











c
b
a
u pertenece a )Im(A
La matriz A está dada por los coeficientes del sistema de ecuaciones, estos coeficientes corresponden a
número que se encuentra delante de cada variable x , y y z , por tanto:














321
211
112
A
a)












































3
2
1
,
2
1
1
,
1
1
2
genFA
Sea AF
c
b
a






































































321
321
321
321
32
2
2
3
2
1
2
1
1
1
1
2




c
b
a









c
b
a
321
321
321
32
2
2










































c
cb
cba
A
c
cb
ca
A
A
c
b
a
321
110
35000
)5(
321
110
2550
)1(
)2(
321
211
112
21
32
31





















 035/3
cbaR
c
b
a
FA
  3/)( 3
R
OAXRXANu 
Sea )(ANu
c
b
a
X 



















































0321
0530
0000
)1(
0321
0530
0530
)1(
)2(
0321
0211
0112
21
32
31
A
A
A

77. 053  cb 032  cba





















 cbcbaR
c
b
a
ANu 53032/)( 3
  3
3 ;/)Re( RXYAXRYA 
Sea )Re(A
c
b
a
Y 





















































c
cb
cba
A
c
cb
ca
A
A
c
b
a
321
530
000
)1(
321
530
2530
)1(
)2(
321
211
112
21
32
31
0 cba





















 0/)Re( 3
cbaR
c
b
a
A
b)
Para que el vector u pertenezca a la imagen de A debe cumplir con la condición de la misma, cabe recalcar
que la imagen de una matriz es también conocida como el recorrido de una matriz
Sea











c
b
a
u , donde bac  2
02
02
0)2(
0




ba
baba
baba
cba
Pero hay que tener en cuenta que ba 2 no necesariamente tiene que ser igual a 0
)Im(Au 

78. Escuela Superior Politécnica del Litoral
Instituto de Ciencias Matemáticas
Solución y Rúbrica de la Tercera Evaluación de Algebra Lineal
Nombre:…………………………………………………………………………………….. Paralelo:………………
Firma:………………………………………………………………………………………… Septiembre 15,2011
1.- (20 puntos) Defina:
Núcleo de una transformación lineal.- Sea T: V  W una transformación lineal. El núcleo de T es
el conjunto de todos los vectores de V que mediante T se transforman en el neutro aditivo de W.
Recorrido de una matrizAmxn.- Es el conjunto de todos los vectores Y de Rm
, para los que existe un
vector X de Rn
tal que AX = Y.
Conjunto ortonormal de vectores.- Es un conjunto {v1,v2,v3,…vn} de vectores de un espacio
vectorial con producto interno tal que (vi,vj)= 0 si ij , y es igual a 1 si i=j.
Conjunto generador de un Espacio Vectorial.- Es un conjunto {v1,v2,v3,…vn} de vectores de V tal
que todo vector de V puede escribirse como combinación lineal de los vectores del conjunto.
2.- (20 puntos) Considere el siguiente sistema de ecuaciones lineales:
x + y + z = 2
2x + 3y + 3z = 5
2x + 3y + (k2-1)z= k+3
Desempeño
Insuficiente Regular Excelente
No escribe definiciones
coherentes , o deja el
espacio vacío
Presente una idea relacionada con el
concepto pera falta precisión o añade
elementos adicionales incorrectos.
Presenta en forma explícita todos
los elementos claves de los
conceptos.
0-1 2-4 5

79. Determine los valores de k para que el sistema lineal resultante tenga:
a) Solución única
b) Infinitas soluciones
c) Ninguna solución
Representamos el sistema haciendo uso de la matriz aumentada:










 3132
5332
2111
2
kk 


Empleando operaciones elementales con renglones, nos queda:










 2400
1110
1001
2
kk 


Si 2k , el sistema tiene infinitas soluciones: 1x , 1 zy
Si 2k , no hay solución para el sistema y la matriz aumentada se ve de la siguiente manera:










 4000
1110
1001



Si k toma cualquier valor que no sea ni 2 ni 2 , la única solución del sistema es:
1x ,
2
1



k
k
y ,
2
1


k
z
CRITERIO PUNTAJE
Plantea la matriz aumentada correctamente hasta 3
Realiza adecuadamente las operaciones
elementales con renglones
hasta 4
Concluye, justificando, que con 2k el sistema
tiene infinitas soluciones
hasta 4
Concluye, justificando, que con 2k el sistema
es inconsistente
hasta 4
Concluye, justificando, que si 2k y 2k ,
el sistema tiene solución única y encuentra dicha
solución única
hasta 5

80. 3.- (20 puntos) Sea T:VW una transformación lineal. Si dim V= 3 y dim W = n,
demuestre que:
a) Si n= 3, T es inyectiva si y solo si T es sobreyectiva.
b) Si n > 3, T no es sobreyectiva
c) Si T es inyectiva, n ≥ 3
PRUEBA:
a) = 3
i) PD: Si T es inyectiva, entonces T es sobreyectiva.
Si T es inyectiva, entonces = 0.
Por el teorema de la dimensión, tenemos: + = = 3
→ = 3 (ya que = 0)
→ = dim
→
ii) PD: Si T es sobreyectiva, entonces T es inyectiva.
Si T es sobreyectiva, entonces =
→ = dim = 3
Por el teorema de la dimensión, tenemos: + = = 3
→ = 0 (ya que = 3)
→
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , deja el
espacio vacío o solo
intenta adivinar
Demuestra la bicondicional
en una sola dirección.
Demuestra la bicondicional
en una sola dirección e
intenta demostrarla en la
otra dirección
Demostración
completa y
correcta
0 1-4 5-7 8

81. b) Para este caso se puede demostrar la contrarrecíproca de la proposición dada:
PD: Si T es sobreyectiva, entonces ≤ 3.
Si T es sobreyectiva, entonces = .
→ = dim =
Por el teorema de la dimensión, tenemos: + = = 3
→ + = 3
→ = 3 −
Por otro lado, tenemos que:
( ) ≥ 0
→ − ≤ 0
→ 3 − ≤ 3
→ ≤ 3
c) PD: Si T es inyectiva, n ≥ 3
Si T es inyectiva, entonces = 0
Por el teorema de la dimensión, tenemos: + = = 3
→ = 3
Por otro lado, ya que Im (T) es un subespacio vectorial de W, se tiene que:
( ) ≤ dim
→ 3 ≤
→ ≥ 3
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , deja el
espacio vacío o solo
intenta adivinar
Determina la
contrarrecíproca de la
proposición y utiliza el
teorema de la dimensión
pero no logra plantear
desigualdad alguna que
sirva para la demostración
Determina la
contrarrecíproca de la
proposición, utiliza el
teorema de la dimensión y
plantea una desigualdad
que sirve para la
demostración pero no
determina la conclusión.
Demostraciones
completas y
correctas
0 1-3 4-5 6

82. 4.- (20 puntos) En el espacio P2, se define el producto escalar:
< p, q > = p (−1) q (−1) + p (0) q (0) + p (1) q (1).
a) Obtenga el complemento ortogonal de W = gen {1}.
c) Determine los polinomios p(x) tales que proyW p(x) = ½.
d) Determine los polinomios de P1 que formen un ángulo de 60 grados con x2.
b) Encuentre la proyección ortogonal de x2− 1 sobre S = gen { 1, x }
SOLUCION:
a) : = + + ∕ 〈 + + , 〉 = 0; ∀ ( ) ∈
Ya que W = gen {1}, entonces una base de W es B = {1}. Con esto:
= + + ∕ 〈 + + , 1〉 = 0
→ − + 1 + 1 + + + 1 = 0
→ 2 + 3 = 0
→ = + + / 2 + 3 = 0, ∈
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , deja el
espacio vacío o solo
intenta adivinar
Determina que =
0, utiliza el teorema de la
dimensión pero no logra
determinar el rango de T.
Determina que =
0, utiliza el teorema de la
dimensión y determina el
rango de T; pero no plantea
una desigualdad que sirva
para la demostración.
Demostraciones
completas y
correctas
0 1-3 4-5 6
Desempeño

83. b) Definamos : = = + + / = 1/2
Para esto, necesitamos una base ortonormal de W.
A partir de la base B = {1}, tenemos:
‖1‖ = 〈1,1〉 = 1 1 + 1 1 + 1 (1) = √3
Con lo que una base ortonormal de W es =
√
Entonces,
( )
= 〈 , 〉 , donde =
√
→ 〈 + + ,
1
√3
〉
1
√3
= 1/2
→ − +
1
√3
+
1
√3
+ + +
1
√3
1
√3
= 1/2
→
2
3
+ = 1/2
→ = + + /
2
3
+ =
1
2
, ∈
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , deja el
espacio vacío o solo
intenta adivinar
Indica que B = {1} es una
base de W y solo define el
complemento ortogonal
de W
Indica que B = {1} es una
base de W y determina el
complemento ortogonal
de W pero comete
errores de cálculo o no
determina correctamente
las condiciones.
Cálculos y
condiciones
correctas.
0 1-2 3-4 5
Desempeño

84. c) Definamos : = = + / 60
60 =
〈 + , 〉
‖ + ‖‖ ‖
1
2
=
− + 1 + 0 + + 1
〈 + , + 〉 〈 , 〉
1
2
=
2
− + − + + + + + 1 1 + 0 0 + 1 1
1
2
=
2
√ − 2 + + + + 2 + √2
1
2
=
2
√2 + 3 √2
4 + 6 = 4
4 + 6 = 16
2 − 5 = 0
→ = + / 2 − 5 = 0
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , deja el
espacio vacío o solo
intenta adivinar
Determina la base
ortonormal de W y solo
plantea la formula que le
permitiría determinar la
proyección.
Determina la base
ortonormal de W y calcula
la proyección pero comete
errores de cálculo o no
determina correctamente
las condiciones.
Cálculos y
condiciones
correctas.
0 1-2 3-4 5
Desempeño

85. d) Para este caso primero debemos determinar una base ortonormal de S.
Siendo = 1, una base de S; con esto determinamos una base ortonormal
= , por el proceso de Gram – Schmidt.
‖1‖ = 〈1,1〉 = 1 1 + 1 1 + 1 (1) = √3
→ =
1
√3
∗
= − 〈 , 〉
∗
= − 〈 ,
1
√3
〉
1
√3
∗
= − − 1
1
√3
+ 0
1
√3
+ 1
1
√3
1
√3
∗
=
‖ ‖ = 〈 , 〉 = − 1 − 1 + 0 0 + 1 (1) = √2
→ =
1
√2
De ahí que, la base ortonormal de S es =
√
,
√
Luego, la proyección es:
= 〈 − 1, 〉 + 〈 − 1, 〉
= 〈 − 1,
1
√3
〉
1
√3
+ 〈 − 1,
1
√2
〉
1
√2
Insuficiente Regular Satisfactorio Excelente
No realiza
procesos
coherentes , deja
el espacio vacío o
solo intenta
adivinar
Solo plantea
correctamente la
formula que le
permitiría determinar
el ángulo entre loa
vectores
Plantea correctamente la formula
que le permitiría determinar el
ángulo entre loa vectores, realiza
los cálculos pero comete errores
en los mismos o no determina
correctamente las condiciones.
Cálculos y
condiciones
correctas.
0 1-2 3-4 5

86. = 0
1
√3
+ − 1
1
√3
+ 0
1
√3
1
√3
+ 0 −
1
√2
+ − 1 0 + 0
1
√2
1
√2
= −
1
3
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , deja el
espacio vacío o solo
intenta adivinar
Plantea el hecho de que es
necesario determina una
base ortonormal de S y al
calcularla comete errores.
Determina correctamente
una base ortonormal de S
pero comete errores al
calcular la proyección.
Cálculos
correctos.
0 1-2 3-4 5

87. 5.-(20 puntos) Sea T: P2P2 la transformación lineal definida por:
T(ax2+bx+c)=2ax2+(3a+2b+c)x+(4a+b+2c)
De serposible,determineuna base de P2 respecto de la cual la matriz que representa a T
sea una matriz diagonal.
La representación matricial de T con respecto a la base  2
1 x,x,B  es:











200
321
412
A
El polinomio característico de la matriz A , es:      312  p
Los valores propios de A , son: 321 ,,
Entonces, la matriz A es diagonalizable; ya que es una matriz cuadrada de tamaño 3 con 3 valores
propios distintos. Por tanto, la transformación lineal T es diagonalizable.
Con 11  , se obtiene:





















0
1
1
1 genE
De aquí se obtiene que: xv  11
Con 22  , se obtiene:























1
4
3
2 genE
De aquí se obtiene que: 2
2 43 xxv 

88. Con 33  , se obtiene:





















0
1
1
3 genE
De aquí se obtiene que: xv 13
Finalmente, la matriz asociada a T con respecto a la base  x,xx,x*B  1431 2
es
la matriz diagonal:











300
020
001
D
CRITERIO PUNTAJE
Encuentra correctamente la matriz asociada a T
con respecto a la base canónica de 2P
hasta 2
Calcula correctamente los valores propios de la
representación matricial de T
hasta 4
Determina con argumentos que T es
diagonalizable
hasta 2
Encuentra los 3 vectores de la base *B solicitada
(hasta 4 puntos por cada vector)
hasta 12

89. Solución y Rúbrica 2da Evaluación de Algebra Lineal
1.- Corrija o confirme las siguientes definiciones:
Definición Propuesta Criterio del Estudiante
Operador Diagonalizable.- Sea T:VV un
operador lineal. Se dice que T es diagonalizable si
y solo si existe una base B de V tal que la
representación matricial de T respecto a B es una
matriz diagonal.
Esta Correcta
Producto interno real en V.- Es una función de f:
VxV R tal que:
1) v  V , f(v,v)≥0
2) v1,v2  V , f(v1,v2)=f(v2,v1)
3) α  R, v1,v2  V, f(αv1,v2)=αf(v1,v2)
4) v1,v2,v3  V, f(v1,v2+v3)=f(v1,v2)+f(v1,v3)
Falta en la condición 1 que el product interno
de un vector consigo mismo es cero solo
cuando el vector es el neutron aditivo de V.
Valor propio de un operador T:VV.- Si   K es
un escalar para el que existe un vV tal que
T(v)= v, entonces  es un valor propio de T.
Falta especificar que el vector v tiene que ser
diferente del neutro aditivo de V.
Espacios Isomorfos.- Dos espacios V y W son
isomorfos si y solo si toda función de V en W es
un isomorfismo.
En vez del cuantificador universal debe decir
que es posible construir un isomorfismo de V
en W.
Para cada defición:
Desempeño
Insuficiente Regular Excelente
Califica o corrige
incorrectamente
Añade condiciones innecesarias o
escribe algo erroneo.
Hace las puntualizaciones y
correcciones correctas.
0 1-2 3

90. 2.- Califique las siguientes proposiciones como verdaderas o falsas. Justifique formalmente su
calificación.
a) Sea : → una transformación lineal. Si = 0 es un valor propio de , entonces es
inversible.
Solución:
Sea A la matriz asociada a la transformación lineal T. La ecuación característica es:
det − = 0
Como el valor propio de T es igual a cero, entonces det A es igual a cero, por lo tanto A no es
inversible y esto implica también que T no lo es. La proposición es FALSA. También podemos
concluir que la nulidad de A (y de T) no es cero por lo que T no es inyectiva , no es biyectiva y por
lo tanto no es inversible.
b) Si A  M2x2 entonces el polinomio característico de A es:
p() =2
- (traza de A) + det(A)
Solución:
Sea A una matriz de M2x2 : =
Luego, el polinomio característico es: = − − −
Realizando las operaciones indicadas: = − + + − . Finalmente:
= − + det
Por lo tanto la proposición es VERDADERA.
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , solo
califica o deja el
espacio vacío
Asocia el hecho de que una
transformación lineal tiene
asociada una matriz, pero no
plantea la ecuación
característica.
Plantea la ecuación
característica, utiliza el
valor de = 0 , pero
concluye equivocadamente
.
Califica y prueba
correctamente.
0 1-3 4-6 7

91. c) Sea V un espacio vectorial con producto interno (,). Si para todo v  V se tiene que
(v,u)=0 entonces u es el vector neutro aditivo de V.
Solución: Como vale para todo v en V también vale para u , por lo que (u,u)= 0 y por
definición de producto interno esto implica que u es el neutro aditivo de V.
Por lo tanto, la proposición es VERDADERA.
d) Es posible construir un operador lineal T: P2  P2 tal que:
T(x+1)=x T(x2
-1)= 2x y (T ° T)(x2
+x)=0
Solución: Se escribe el vector: + 1 + − 1 =
+ .
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , solo califica
o deja el espacio vacío
Plantea una matriz
cuadrada de 2x2 y
escribe el polinomio
característico
correspondiente.
Realiza las operaciones
necesarias pero no
compara o concluye
equivocadamente
Califica y prueba
correctamente.
0 1-3 4-6 7
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , solo califica
o deja el espacio vacío
Asocia el hecho de
que u pertenece al
complemento
ortogonal de V.
Analiza la propiedad de
que u deba ser
ortogonal a todos los
vectores de V
Califica y prueba
correctamente.
0 1-3 4-6 7

92. Aplicando la transformación lineal T, queda:
+ 1 + − 1 = +
+ = + 2 = 3 .
+ = 3 =
Se observa que los vectores: x+1, x2-1 y 3x forman una base de P2, por ello:
+ + = + 1 + − 1 + 3
+ + = + + 3 + −
De donde obtenemos:
= ; = + ; =
− −
3
Por ello, aplicando la transformación lineal T:
+ + = + + 1 + − 1
+ + = 3 +
También a partir de los datos se puede determinar que T(x)=0, T(1)=x y T(x2)=3x y
obtener la regla de correspondecia.
Tema 3
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes , solo califica
o deja el espacio vacío
Escribe el vector x2
+x
como combinación
lineal de los vectores
x+1 y x2
-1. Y aplica la
transformación lineal
al resultado
obteniendo T(x2
+x).
Observa que se ha
obtenido una base para
P2 y trata de escribir la
combinación lineal del
vector típico sin
resolver el sistema de
ecuaciones
correspondiente.
Califica y prueba
correctamente.
0 1-3 4-6 7

93. Sea A una matriz simétrica de nxn con componentes reales. Si  es un valor propio de A,
entonces  es un número real.
Demostración
Premisas:
Sea A una matriz simétrica
Sea  un valor propio de A
Sea X un vector propio de A asociado al valor propio 
Supóngase que a bi  
Se debe demostrar que b=0
AX X
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( ) 0
( )( ) 0
T
T
AX X X X
AX X X X
X AX X X
X AX X X
X X X X
X X




 
 




 
 
Pero ( ) 0X X  por ser X vector propio, entonces
0  
( ) ( ) 0
0
2 0
0
es un número real
a bi a bi
a bi a bi
bi
b

   
   



También puede emplearse otra demostración equivalente.
Rúbrica:

94. Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza
procesos
coherentes o
deja el espacio
vacío.
Utiliza como premisas la
definición de vector
propio y la aplicación del
producto interno, y no
continua con la
demostración. También
puede intentarlo con
otros métodos válidos,
pero sin concluir
Además de lo anterior, se
apoya en las propiedades
de una matriz simétrica y
las correspondientes al
producto interno sobre el
vector propio, pero no
concluye respecto a la
componente imaginaria
del valor propio.
Demuestra
correctamente
basándose en
definición y
propiedades de
vectores propios,
matriz simétrica y
producto interno u
otras pertinentes
0 1 - 5 6 - 9 10
TEMA 4
Sea : → un operador lineal definido por una matriz ortogonal Q tal que = .
Considerando el producto interno estándar de pruebe que:
a.- ∀ ∈ , ‖ ( )‖ = ‖ ‖
b.- ∀ , ∈ , , = 0 ⇒ ‖ ( )‖ + ‖ ( )‖ = ‖ + ( )‖
Prueba:
a.- ∀ ∈ , ‖ ( )‖ = ‖ ‖
Ya que ( ) ∈ , tenemos:
‖ ( )‖ = , ( )
= ,
=
=
= √ ; ya que Q es Ortogonal ( = )

95. = √
= ,
= ‖ ‖
b.- ∀ , ∈ , , = 0 ⇒ ‖ ( )‖ + ‖ ( )‖ = ‖ + ( )‖
‖ + ( )‖ = + , + ( )
= , + 2 , + ,
= ‖ ( )‖ + 2 , + ‖ ( )‖
Por otro lado:
, = , = = = = = , = 0
Por lo tanto:
‖ + ( )‖ = ‖ ( )‖ + ‖ ( )‖
a.-
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes, deja el
espacio vacío o solo
intenta realizar la
demostración.
Determina la norma
de ( ) pero no
aplica la isometría
correspondiente.
Determina la norma de
( ) y aplica la
isometría
correspondiente pero
comete algún error o
no usa la definición de
matriz ortogonal.
Demostración
correcta.
0 1 2 - 3 4
b.-

96. Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes, deja el
espacio vacío o solo
intenta realizar la
demostración
Determina la norma
al cuadrado
de + ( )
pero no aplica la
isometría
correspondiente.
Determina la norma al
cuadrado de +
( ) y aplica la
isometría
correspondiente pero
comete algún error o
no usa la definición de
matriz ortogonal.
Demostración
correcta
0 - 1 2 - 3 4 - 5 6
Tema 5
Se desea bosquejar el gráfico del conjunto solución de la siguiente ecuación de segundo orden
4 − 12 + 9 − 8√13 − 14√13 + 117 = 0
a) Determine la forma cuadrática correspondiente:
, = 4 − 12 + 9
b) La matriz asociada a la forma cuadrática con respecto a la base canónica está dada por:
=
4 − 6
− 6 9
El polinomio característico de está dado por:
= det −
= − 13
Por lo tanto los valores propios de son:
λ = 0 ∨ λ = 13

97. A partir de aquí se tiene los espacios asociados a cada uno de los valores propios.
= , : = 3 /2
= , : = − 2 /3
Los vectores propios asociados a cada uno de los valores propios.
= 3,2
= − 2,3
La matriz que diagonaliza ortogonalmente a está dada por:
=
1
√13
3 − 2
2 3
√
3 − 2
2 3
=
( ) − ( )
( ) ( )
, por lo tanto se tiene que:
=
√
y =
√
, obteniendo que = 0,588
Dado que:
=
1
√13
3 − 2
2 3
`
`
Entonces:
=
√
3 ` − 2 ` ; =
√
2 ` + 3 `
reemplazando las relaciones dadas se tiene la ecuación transformada a los nuevos ejes.
` − 4 ` − 2 + 9 = 0
` − 1 = 4 ` − 2
La misma que representa gráficamente a una parábola.

98. Rúbrica:
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Determina la forma
cuadrática
correspondiente y
diagonaliza
ortogonalmente la
matriz asociada a la
forma cuadrática.
Además de lo
anterior, determina la
medida del ángulo de
rotación así como
transforma la
ecuación dada a los
nuevos ejes
Además de todo lo
anterior, identifica la
cónica y lo grafica
pertinentemente.
0 1 - 4 5 -7 8-10
20 10 0 10 20
20
10
0
10
20
X’(+)
Y’(+)
X(+)
Y(+)

99. RUBRICA EXAMEN FINAL ALGEBRA LINEAL FEBRERO 2012
Desempeño
Insuficiente Regular Satisfactorio Excelente
Califica
incorrectamente o
deja el espacio vacío.
Identifica que la
definición es incorrecta
pero se equivoca al
identificar el error
La corrección mejora
la definición pero no
es completa
Indica la corrección de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño
Insuficiente Regular Satisfactorio Excelente
Califica
incorrectamente o
deja el espacio vacío
Resuelve la definición
para matriz
diagonalizable
Falta precisión al
corregir.
Indica las correcciones
de manera correcta.
0 1 - 4 5 - 8 9-10

100. Tema 2 (10 puntos)
Sean y dos espacios vectoriales de dimensión finita tal que , , … , , , , … ,
es una base de . Sea : → una transformación lineal. Demuestre que, Si , , … , es
una base del ( ), entonces , … , es una base de la ( ).
∀ ∈ ∃ ∈ ℝ = + + ⋯ + + + + ⋯ +
= + + ⋯ + + + + ⋯ +
= + + ⋯ + + + + ⋯ +
= + + ⋯ + + + + ⋯ +
Pero se conoce que = 0 ∀ = 1, … , por ser elementos del ( ), entonces:
( ) = + + ⋯ +
Dado que ∈ ( ) entonces = , … ,
+ + ⋯ + = 0
+ + ⋯ + = 0
Por lo que:
+ + ⋯ + ∈ ( )
Al pertenecer al ( ), entonces se podrá expresar como combinación lineal de la base del
subespacio.
+ + ⋯ + = + + ⋯ +
+ + ⋯ + + (− ) + (− ) + ⋯ + (− ) = 0
Dado que , , … , , , , … , es una base de , entonces la combinación lineal de
estos vectores igualados al neutro tiene solución única, es decir,
= 0 ∀ = 1, … . , , + 1, + 2, … . ,
Por lo que el conjunto , … , es linealmente independiente en .
Por lo tanto es una base de .

101. Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Identifica que debe
probar la
independencia lineal y
la capacidad de generar
la imagen
Prueba correctamente
una de las
propiedades pero falla
en la otra
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Particulariza los
vectores para verificar
la linealidad
Aplica la definición de
transformación lineal
correctamente, pero
con error de cálculos o
no concluye.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

102. Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Aplica T a la base
canónica
La matriz asociada
tiene algún error de
cálculo
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Aplica correctamente la
definición de nucleo de
T
Aplica el concepto de
núcleo, pero al
resolver comete
errores.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

103. Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Determina el rango de
T o una base para la
imagen de T.
Demuestra conocer la
definición de suma
directa o el teorema
equivalente pero tiene
errores de calculo
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño

104. Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Asocia la nulidad de T
con la existencia de la
inversa
Respuesta correcta
pero alguna
afirmación errónea.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Tema 4 (10 puntos)
(a) Considere la ecuación de una forma cuadrática dada por:
5 + 6 + 5 − 16 − 16 − 16 = 0
Consideremos la forma cuadrática:
, = 5 + 6 + 5
La matriz asociada a la forma cuadrática con respecto a la base canónica está dada por:
=
5 3
3 5
Determinemos los valores propios de :
− = 0
5 − − 9 = 0
Entonces los valores propios de son = 8 = 2
Los espacios propios asociados a cada valor propio, así como sus respectivas bases ortonormales
están dados por:
= , : = ; ℝ; =
√
1,1
= , : = − ; ℝ; =
√
− 1,1
Por lo tanto, la matriz que diagonaliza ortogonalmente a está dada por:

105. =
1
√2
−
1
√2
1
√2
1
√2
Por lo que la forma cuadrática se puede expresar de la forma:
′ , = 8 + 2
Adicionalmente se conoce que:
=
1
√2
−
1
√2
1
√2
1
√2
Por lo que:
=
1
√2
−
1
√2
=
1
√2
+
1
√2
Remplazando en la expresión dada se tiene:
8 + 2 − 16
1
√2
−
1
√2
− 16
1
√2
+
1
√2
− 16 = 0
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Determine la forma
cuadrática
correspondiente y los
valores y vectores
propios de la matriz de
la forma cuadrática
Reconoce la
sustitución apropiada
pero tiene errores de
cuentas
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

106. Simplificando:
4 + − 8√2 − 8 = 0
4 − √2 + = 16
− √2
4
+
16
= 1
Lo cual representa gráficamente una elipse con centro en el punto , = √2, 0 , eje mayor
paralelo al eje con una longitud del semieje mayor de = 4 y longitud del semieje menor de
= 2.
Para determinar la medida del ángulo de rotación de los ejes originales, se conoce que:
1
√2
−
1
√2
1
√2
1
√2
=
( ) − ( )
( ) ( )
Por lo tanto, =
Con base en lo anterior, la gráfica de la forma cuadrática se muestra a continuación:

107. 4 2 0 2 4
4
2
0
2
4
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Halla la matriz Q,
reconoce el ángulo de
rotación
Además escribe de
manera correcta la
ecuación de la cónica
pero no realiza el
bosquejo correcto.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

108. Derivando y evaluando en 1, queda: 2a + b = 0; de donde b=-2a. Por lo tanto una base de H es:
Base de H = { x2
– 2x, 1}
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Deriva erróneamente y
por ello la base es
incorrecta.
Deriva correctamente,
pero expresa la base
de manera errónea.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

109. Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Realiza erróneamente
el producto interno.
Obtiene el sistema
homogéneo de
manera correcta, pero
presenta errores en la
respuesta.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

110. TEMA 6
Dada la matriz =
1
− 1 1 − 1
1 0 2
, ∈ ℛ.
a) Demostrar que los valores propios de son independientes del valor del parámetro.
b) Demostrar que = 0 si y solo si la matriz es diagonalizable.
c) Determinar la matriz tal que = .
SOLUCION
a) Para hallar los valores propios de , utilizamos la ecuación característica det ( − ) = 0
1 −
− 1 1 − − 1
1 0 2 −
= 0
1
1 − − 1
+ 2 −
1 −
− 1 1 −
= 0
− − 1 − + 2 − 1 − + = 0
− 2 − + 2 − 1 − + = 0
2 − − + 1 − + = 0
2 − 1 − = 0
= 2 , = 1 , ∀ ∈ℛ
= 1 , = 2
Es decir que los valores propios de la matriz son independientes del parámetro.
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Trata de calcular la
proyección del vector
dado pero lo realiza con
errores.
Calcula una de las
proyecciones del
vector correctamente,
pero no comete algún
error al calcular la
segunda proyección.
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño
Insuficiente Regular Satisfactorio Excelente

111. b) Para que sea diagonalizable, se debe cumplir que:
= ℇ ∧ = ℇ
Para = 2 no hay problema puesto que = 1 y además 1 ≤ ℇ ≤ = 1 ,
de ahí que = ℇ .
Para = 1 , tenemos:
ℇ = − =
0
− 1 0 − 1
1 0 1
=
0
− 1 0 − 1
1 0 1
=
0
0
0
Resolviendo el sistema de ecuaciones homogéneo por el método de Gauss, tenemos:
0
− 1 0 − 1
1 0 1
0
0
0
∼
1 0 1
0
− 1 0 − 1
0
0
0
∼
1 0 1
0
0 0 0
0
0
0
De ahí que:
ℇ =
−
− ∈ ℛ , ≠ 0
−
, ∈ ℛ , = 0
Por lo tanto, es diagonalizable si y solo si = 0; puesto que ℇ = 2 = .
No realiza procesos
coherentes o deja el
espacio vacío.
Plantea la ecuación
característica para
determinar los valores
propios
Al resolver la ecuación
no logra eliminar el
parámetro
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño
Insuficiente Regular Satisfactorio Excelente

112. c) Para hallar la matriz diagonalizante, solo falta determinar el vector propio de asociado a
= 2.
ℇ = − 2 =
− 1 0 0
− 1 − 1 − 1
1 0 0
=
− 1 0 0
− 1 − 1 − 1
1 0 0
=
0
0
0
ℇ = −
0
∈ ℛ
Por lo tanto =
0 − 1 0
− 1 0 1
1 1 0
es la matriz que diagonaliza a la matriz con forma
diagonal =
2 0 0
0 1 0
0 0 1
.
No realiza procesos
coherentes o deja el
espacio vacío.
Determina la
multiplicidad algebraica
de los valores propios
Asocia correctamente
la multiplicidad
geométrica con la
posibilidad de
diagonalización
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10
Desempeño
Insuficiente Regular Satisfactorio Excelente
No realiza procesos
coherentes o deja el
espacio vacío.
Calcula los vectores
propios
Intenta determinar la
matriz pedida con los
vectores calculados
Realiza el ejercicio de
manera correcta.
0 1 - 4 5 - 8 9-10

113. Algebra Lineal – Tercera Evaluación 2do Semestre
2011-2012 – Solución y rúbrica
Tema 1
(a) ⟸: Se supone que ∈ . Sea un vector de . Como ⊂ ∪ { } , entonces ( ) ⊂
( ∪ ) . Ahora demostramos que ( ∪ ) ⊂ ( ) . Sea ∈ ∪ .
Entonces = + + + ⋯ + , con , , … , ∈ ⊂ ( ). Como ∈
( ), y como ( ) es un subespacio vectorial, entonces ∈ ( ). Por lo tanto
( ∪ ) ⊂ ( ), y entonces = ( ∪ ).
⇒: Se supone que = ∪ . Como ∈ ∪ , entonces ∈ ( ∪
) y por tanto ∈ ( ). Pero no se puede demostrar que ∈ . Contraejemplo: en
el espacio vectorial ℝ, si = 1 y = 2 , = ∪ = ℝpero ∉ .
Entonces la propiedad es falsa.
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Califica como verdadero pero demuestra correctamente el
reciproco
2-5
Regular Califica como falso dando se cuenta que la implicación directa no
puede ser verdadera, pero no lo demuestra formalmente(no da
un contraejemplo)
6-8
Excelente Califica como falso dando la justificación y un contraejemplo
adecuado.
9-10
(b) Demostramos la doble inclusión:
⊂: Sea ∈ , . Entonces existe ∈ , tal que = . Como
∈ , , entonces se escribe como una combinación líneal: = + .
Entonces = = + = + ( ) por linealidad de T. Por lo
tanto ∈ ( ), ( ) , y entonces , ⊂ ( ), ( )
⊃: Sea ∈ ( ), ( ) . Entonces w se escribe como una combinación lineal: =
+ = + . Por lo tanto ∈ , , entonces
( ), ( ) ⊂ , .
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Solo demuestra una de las dos inclusiones 2-5
Regular Demuestra las dos inclusiones pero con imprecisiones 6-8
Excelente Demuestra las dos inclusiones rigurosamente 9-10

114. (c) Sea ∈ . Calculamos :
‖ − ‖ = ‖ − + − ‖ = − + − | − + − =
‖ − ‖ + 2 − | − + ‖ − ‖ .
Sabemos que ⨁ , entonces se descompone como la suma de un vector de y un
vector de , el vector de siendo la proyección de v sobre . Entonces = + ´,
con ´ = − ∈ . Como es un subespacio vectorial, entonces − ∈ , y
por lo tanto − | − = 0. Entonces ‖ − ‖ = ‖ − ‖ + ‖ − ‖ ≥
‖ − ‖ .
Deficiente No conteste o lo que escribe no está relacionado con el tema 0-1
Insuficiente Trata de calcular ‖ − ‖ pero no demuestra que − y
− son ortogonales
2-5
Regular Demuestra la propiedad pero con imprecisiones 6-8
Excelente Demuestra la propiedad rigurosamente 9-10
Tema 2
(a) No necesita solución…
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Demuestra la propiedad pero con imprecisiones 2-5
Regular Demuestra la propiedad a partir de la definición 6-8
Excelente Demuestra la propiedad a partir del teorema de caracterización 9-10
(b) Para demostrar que es inyectiva, demostramos que = 0ℝ , porque T es una
transformación lineal. Sea = ( , , … , ) ∈ . Entonces ( )= +
⋯ + = 0 . Como , , … , forman una base de , son linealmente
independientes. Por lo tanto = = ⋯ = = 0 y = 0ℝ .
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Trata de demostrar que el núcleo contiene solamente el cero
vector pero no utiliza la independencia lineal de , , … ,
2-5
Regular Demuestra la propiedad pero con imprecisiones 6-8
Excelente Demuestra la propiedad rigurosamente 9-10
(c) Como dim = dim ℝ = y como es inyectiva, entonces por teorema es
biyectiva.
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Trata de aplicar el teorema sobre isomorfismos o el teorema de la
dimensión pero no concluye
2-5
Regular Demuestra la propiedad pero con imprecisiones 6-8

115. Excelente Demuestra la propiedad rigurosamente 9-10
Tema 3
(a) Se puede denotar que los polinomios 1 + + , − 1, y 1 − 2 + son linealmente
independientes, entonces forman una base de , porque la dimensión de es igual a 3.
Sea = + + un polinomio de . Descomponemos sobre la base
1 + + , − 1, 1 − 2 + , es decir escribimos como una combinación lineal
de 1 + + , − 1, y 1 − 2 + :
+ + = 1 + + + − 1 + (1 − 2 + )
Esta ecuación nos da el sistema siguiente, , , siendo las incógnitas:
+ + =
− 2 =
− + =
Al resolver este sistema se obtiene = , = , = .
Entonces = 1 + + + − 1 + 1 − 2 + =
0 + − 1 + 3 − 6 + 3 =
− + − + 2 − + ( − ).
Deficiente Denota que 1 + + , − 1, y 1 − 2 + forman una base
de
0-1
Insuficiente Tratan de descomponer un polinomio típico sobre esta base pero
no concluye y no trata de aplicar la transformación T al polinomio
obtenido.
2-5
Regular Desarrolle el procedimiento correcto pero se equivoca en los
cálculos
6-8
Excelente Obtiene la regla de correspondencia con una demostración
rigurosa
9-10
(b) A partir de la regla de correspondencia de , se obtiene la representación matricial de
con respecto a la base canónica: =
1 − 1 0
− 1 2 − 1
0 − 1 1
. Se puede verificar que es una
matriz simétrica.
Calculamos los valores propios de . El polinomio característico es igual a
1 − − 1 0
− 1 2 − − 1
0 − 1 1 −
= 1 −
2 − − 1
− 1 1 −
− − 1
− 1 − 1
0 1 −
=

116. 1 − ( − 3) . Entonces los valores propios de son 0, 1 y 3.
Para el valor propio 0, se obtiene que el espacio propio asociado es
1
1
1
.
Para el valor propio 1, el espacio propio asociado es
1
0
− 1
.
Para el valor propio 3, el espacio propio asociado es
1
− 2
1
.
Los vectores
1
1
1
,
1
0
− 1
y
1
− 2
1
siendo vectores propios asociados a valores propios
diferentes de una matriz simétrica, son ortogonales. Entonces sólo necesitamos
normalizarlos para obtener una base ortonormal:
El vector
1
1
1
normalizado da el vector
1
√3
1
√3
1
√3
, el vector
1
0
− 1
normalizado da el vector
1
√2
0
− 1
√2
, y el vector
1
− 2
1
normalizado da el vector
1
√6
− 2
√6
1
√6
.
Por lo tanto una matriz ortogonal que diagonaliza ortogonalmente es la matriz
1
√3
1
√2
1
√6
1
√3
0 − 2
√6
1
√3
− 1
√2
1
√6
.
Deficiente Verifica que la matriz obtenida es una matriz simétrica. 0-1
Insuficiente Encuentra los valores propios y los vectores propios de 2-5
Regular Ortonormaliza con el proceso de Gram-Schmidt los vectores
propios sin darse cuenta que los vectores propios ya son
ortogonales, y obtiene la matriz
6-8
Excelente Solo normaliza los vectores propios y obtiene una matriz
ortogonal
9-10
(c) A partir de la definición de dada en el enunciado, se puede denotar que 1 + +
= 0, − 1 = 1 × − 1 y 1 − 2 + = 3 × 1 − 2 + . Por lo tanto,
la representación matricial de con respecto a la base 1 + + , − 1,1 − 2 +
es la matriz diagonal
0 0 0
0 1 0
0 0 3
.

117. (d)
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente No se da cuenta que puede obtener directamente la base a partir
de la definición de T, trata de utilizar el resultado del literal
anterior, pero no concluye
2-5
Regular Utiliza el resultado del literal anterior, y obtiene la base. 6-8
Excelente Obtiene la base directamente a partir de la definición de T 9-10
Tema 4
(a) A partir de la definición de , se puede denotar que = ∈ si y sólo si 3 + 2 −
= 0, es decir si y sólo si
3
2
− 1
= 0. Por lo tanto =
3
2
− 1
, y entonces
=
3
2
− 1
=
3
2
− 1
.
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Trata de encontrar una base de H pero no obtiene el
complemento
2-5
Regular Denota que es un hiperplano, obtiene el resultado pero con
imprecisiones en la demostración.
6-8
Excelente Obtiene el complemento ortogonal rigurosamente 9-10
(b) Calculamos la proyección del vector
1
1
2
sobre primero. Sabemos que =
3
2
− 1
. Normalizamos el vector
3
2
− 1
para que sea mas cómodo calcular la
proyección sobre .
3
2
− 1
= √14 entonces =
3 √14⁄
2 √14⁄
− 1 √14⁄
. Entonces la
proyección de
1
1
2
sobre es igual a
3 √14⁄
2 √14⁄
− 1 √14⁄
1
1
2
×
3 √14⁄
2 √14⁄
− 1 √14⁄
=
9 14⁄
6 14⁄
− 3 14⁄
.

118. Entonces el vector
1
1
2
se escribe como la suma
1
1
2
=
9 14⁄
6 14⁄
− 3 14⁄
+
5 14⁄
8 14⁄
31 14⁄
, con el
vector
9 14⁄
6 14⁄
− 3 14⁄
que pertenece a y el vector
5 14⁄
8 14⁄
31 14⁄
que pertenece a .
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Encuentra una base ortonormal adaptada a y pero no
concluye
2-5
Regular Se equivoca en los cálculos, o no justifica rigurosamente los
resultados.
6-8
Excelente Obtiene el resultado y justifica cada etapa de su demostración 9-10
(c) A partir del resultado anterior se obtiene que la proyección ortogonal del vector
1
1
2
sobre es el vector
5 14⁄
8 14⁄
31 14⁄
.
Deficiente No contesta o lo que escribe no está relacionado con el tema 0-1
Insuficiente Trata de aplicar otro procedimiento, pero no alcanza. 2-5
Regular Obtiene el resultado correcto pero no a partir del literal anterior,
o le falta justificar el resultado
6-8
Excelente Obtiene el resultado correcto y justifica su respuesta 9-10
(d) Para aplicar la propiedad dada, primero se necesita definir la matriz . Si = ∈ ,
entonces 3 + 2 − = 0 , es decir que se puede escribir de la forma =
3 + 2
=
1
0
3
+
0
1
2
, entonces los vectores
1
0
3
y
0
1
2
forman una base de , y
por lo tanto =
1 0
0 1
3 2
.
Calculamos
1
1
2
=
1 0
0 1
3 2
1 0 3
0 1 2
1 0
0 1
3 2
1 0 3
0 1 2
1
1
2
=
1 0
0 1
3 2
10 6
6 5
7
5
=
1 0
0 1
3 2
5 14⁄ − 6 14⁄
− 6 14⁄ 10 14⁄
7
5
=
1 0
0 1
3 2
5 14⁄
8 14⁄
=
5 14⁄
8 14⁄
31 14⁄
Deficiente Halla la matriz A 0-1
Insuficiente No se equivoca en el planteamiento del cálculo, y calcula 2-5
Regular Procedimiento correcto pero se equivoca en los calculos 6-8

119. Excelente Obtiene el resultado correcto, detallando los cálculos. 9-10
Tema 5
(a) Para que la matriz
13 12 0
12 13 0
0 0
pertenezca al espacio generado por y , esa matriz
tiene que escribirse como una combinación lineal de y , es decir que la ecuación
13 12 0
12 13 0
0 0
= + =
1 0 0
0 1 0
0 0 1
+
3 2 0
2 3 0
0 0 3
=
+ 3 2 0
2 + 3 0
0 0 + 3
tiene que tener una solución, los reales y siendo las
incognitas. Para que se cumpla esa ecuación, tiene que ser igual a 6 (por el coeficiente
de la segunda fila y de la primera columna), entonces tiene que ser igual a − 5, y por lo
tanto, al calcular el coeficiente de la tercera fila y de la tercera columna, tiene que ser
igual a 13. Recíprocamente, si = 13, se puede verificar que la matriz si pertenece al
espacio generado por y .
Deficiente Escriba la combinación lineal de I y M igual a la matriz dada 0-1
Insuficiente Trata de despejar los coeficientes pero no alcanza 2-5
Regular Termina el procedimiento pero se equivoca en los cálculos 6-8
Excelente Obtiene el resultado correcto, justificando su demostración 9-10
(b) Se denota que = , , , entonces es un subespacio vectorial.
Deficiente Escriba la definición o el teorema de caracterización de un
subespacio vectorial
0-1
Insuficiente Trata de demostrar que E satisface las condiciones de la
definición o del teorema de caracterización pero no alcanza
2-5
Regular Demuestra correctamente por la definición o el teorema de
caracterización
6-8
Excelente Denota que E es un subespacio generado y concluye
directamente
9-10
(c) Calculamos =
3 2 0
2 3 0
0 0 3
=
13 12 0
12 13 0
0 0 9
. Por el resultado del literal (a), no
pertenece al espacio generado por y , entonces, como y son linealmente
independientes, , y son linealmente independientes. Como = , , la
dimensión de es igual a 3.
Deficiente No obtiene el resultado correcto 0-1

120. Insuficiente Obtiene el resultado correcto pero solo justifica una de las dos
propiedades (LI o generador)
2-5
Regular Demuestra las 2 propriedades pero con imprecisiones 6-8
Excelente Demuestra el resultado rigurosamente 9-10
(d) Sean = + + y = + + dos polinomios de . Calculamos
+ = + + + + + = + + + +
+ = + + + + + = + .
Sea ∈ ℝ . Calculamos = + + = + + =
+ + = ( ).
Entonces es una transformación lineal.
Se denota que dim = dim = 3. Entonces para demostrar que es biyectiva, por
el teorema sobre isomorfismos, solo se necesita demostrar que es inyectiva.
Demostramos que = 0 . Sea = + + ∈ tal que =
ℳ ×
. Entonces + + = ℳ ×
. Pero como , y son linealmente
independientes, entonces necesariamente = = = 0, es decir ( ) tiene que ser
igual al polinomio cero. Por lo tanto es inyectiva.
Deficiente Demuestra la linealidad parcialmente 0-1
Insuficiente Demuestra la linealidad y plantea correctamente la demostración
de la biyectividad
2-5
Regular Demuestra la biyectividad pero con algunas imprecisiones en la
demostración
6-8
Excelente Demuestra el resultado rigurosamente 9-10

121. ESCUELA SUPERIOR POLITÉCNICA
DEL LITORAL
INSTITUTO DE CIENCIAS MATEMÁTICAS
TERCERA EVALUACIÓN DE ALGEBRA LINEAL PARA AUDITORÍA
16 de febrero del 2012
Nombre: _____________________________________________________
Paralelo:_______
TEMA 1 (20 puntos)
a) Defina: (10 puntos)
i) Conjunto generador
ii) Espacio fila de una matriz
iii) Espacios isomorfos
iv) Recorrido de una transformación lineal
v) Matrices semejantes

122. b) Determine el valor de verdad de las proposiciones siguientes-
Justifique formalmente su respuesta.
i) Sea WVT : una transformación lineal. Si  ( ) 0vNu T  ,
entonces T es un isomorfismo.
ii) Dada una base ordenada B del espacio vectorial V, entonces las
coordenadas de cualquier vector de V con respecto a la base B son únicas

123. TEMA 2 (20 puntos)
Sea 2V P . Considere los subespacios:
   2
2/ 2 0; , , ( ) / (0) (1)H ax bx c a b c a b c W p x P p p         
Determine:
a) Una base y la dimensión de WH 
b) Si WH  es un subespacio de V
c) Una base y la dimensión de WH 
d) El subespacio WH 

124. TEMA 3 (20 puntos)
Considere el espacio vectorial 3
R y sea  3211 ,, uuuB  una base de 3
R y el conjunto
 3212 ,, vvvB  donde:
1 1 2 2 2 3 3 1 2 3; ;v u u v u u v u u u      
a) Determine la matriz de transición (de cambio de base) de 2B a 1B
b) Si    1
1,1, 1B
w  , determine   2B
w las coordenadas del vector w con respecto a la
base 2B

125. TEMA 4 (20 puntos)
Sea





















 0/3
zyx
z
y
x
H un subespacio vectorial de 3
 .
a) Construya una transformación lineal 2
3
PendeT  tal que:
1
1
0
0
,2
0
1
1
,)( 2






















 
xTxTHTNu
b) Determine











2
1
1
T

126. TEMA 5 (20 puntos)
Sea A la matriz de los coeficientes del sistema lineal:
2 1
3 2 0
2
x
x y z
x z


  
   
Determine:
a) Los valores propios de A.
b) Los espacios asociados a los valores propios de A.
c) Si A es diagonalizable, la matriz D y la matriz C.