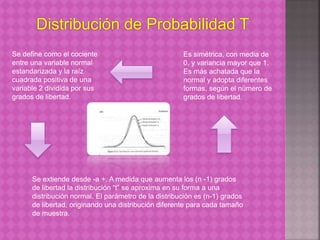
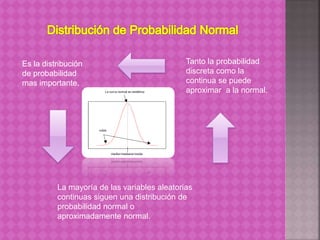
La distribución normal es la más importante en probabilidad y estadística. Tanto la probabilidad discreta como continua pueden aproximarse a la normal. La mayoría de variables aleatorias continuas siguen una distribución normal o aproximadamente normal.

2. Es la distribución
de probabilidad
mas importante.
Tanto la probabilidad
discreta como la
continua se puede
aproximar a la normal.
La mayoría de las variables aleatorias
continuas siguen una distribución de
probabilidad normal o
aproximadamente normal.

3. Ejemplo:
La vida media de una lámpara, según el fabricante, es de 68 meses,
con una desviación típica de 5. Se supone que se distribuye según
una distribución normal En un lote de 10.000 lámparas. a) ¿Cuántas
lámparas superarán previsiblemente los 75 meses?. b) ¿Cuántos
lámparas se estropearán antes de 60 meses?
a)
t = (75 -68)/5 = 1,4
P (X > 75) = (t > 1,4) = 1 - P (t ≤ 1,4) =
1 - 0,9192 = 0,0808
Luego, el 8,08% de las lámparas (808
lámparas) superarán los 75 meses
b)
t = (60 -68)/5 = -1,6
P (X ≤ 60) = (t ≤ -1,6) = P (t> 1,6) = 1 - P (t
≤ 1,6) = 0,0548
Luego, el 5,48% del lote (548 lámparas) no
llegarán probablemente a durar 60 meses

4. Distribución de Probabilidad
Normal Estándar
Es aquella cuya media
es 0 y desviación
estándar 1. No existe
una sola distribución de
probabilidad normal sino
una familia de ellas.
Cada una de las
distribuciones puede
tener una media (μ) o
una
desviación estándar
distinta (σ).
De forma que todas las distribuciones normales pueden convertirse
a la estándar, restando la media de cada observación y dividiendo
por la desviación estándar. Primero, convertiremos la distribución
real en una distribución normal estándar utilizando un valor llamado
Z, o estadístico Z que será la distancia entre un valor seleccionado,
designado X, y la media μ, dividida por la desviación estándar σ.

5. Ejemplo:
Denotemos por z(α) aquel número real tal que P[Z>z(α)] = α
Por ejemplo:
a) z(0,25) = nº que deja un área de 0,25 a su derecha = {tabla} ≈
0,675
ya que P(Z<0,67) = 0,7486 y P(Z<0,68) = 0,7517 .
b) Si queremos calcular un nº real c tal que P(-c<Z<c) = 0,95 , nos
interesa hallar
z(0,025) . Según la tabla, c = z(0,025) = 1,96 ya que
P(Z<1,96) = 0,975 y P(Z<-1,96) = 0,025
a) P(Z<1,52)= 0,9357
b) P(Z>1,52) = {área total = 1} = 1 – P(Z<1,52) = 0,0643
c) P(0<Z<1,52) = P(Z<1,52) – P(Z<0) = {simetría} =
0,9357 – 0,5000 = 0,4357
d) P(-2,1<Z<0) = P(Z<0) – P(Z<-2,1) = {sim+tabla} =
0,5000 – 0,0179 = 0,4821

6. Distribución de Probabilidad Cuadrada
Distribución de Probabilidad T Distribución de Probabilidad F
Se derivan de la distribución
Normal y están relacionadas
con la teoría del muestreo
pequeño n< 30.
Son muy importantes pues
son la base de metodologías
inferenciales, tales como
Intervalos de Confianza y
Pruebas de Hipótesis.
Surgen de transformaciones de variables
aleatorias en las que están involucrados
estadísticos muestrales, tales como la
media y la varianza.

7. Distribución de Probabilidad T
Se define como el cociente
entre una variable normal
estandarizada y la raíz
cuadrada positiva de una
variable 2 dividida por sus
grados de libertad.
Es simétrica, con media de
0, y variancia mayor que 1.
Es más achatada que la
normal y adopta diferentes
formas, según el número de
grados de libertad.
Se extiende desde -a +. A medida que aumenta los (n -1) grados
de libertad la distribución “t” se aproxima en su forma a una
distribución normal. El parámetro de la distribución es (n-1) grados
de libertad, originando una distribución diferente para cada tamaño
de muestra.

8. Ejemplo:
Los valores de las matriculas de estudiantes en una universidad
privada tienen un comportamiento aproximadamente normal,
donde el promedio es de 2.100.000. Se seleccionan 8
liquidaciones, siendo los valores los siguientes: 1.950.000,
2.100.000, 2.250.000, 1.890.000, 2.250.000, 1.950.000, 2.050.000,
2.350.000. Determine la probabilidad de que:
El promedio sea menor de
2.000.000.
· El promedio se encuentre entre
2.000.000 y 2.200.000
· El promedio sea mayor o igual a
2.500.000
Sea X = Liquidación matriculas.
m = 2.100.000 ; s = ?
=2.098.750 s=168.644.8085 n=8
a) P( <2.000.000)=P( <2.000.000)
P(t<(2.000.000-2.100.000)/(168644.8085/2.8284)= P(t<-
1.677)

9. Distribución de Probabilidad F
Una variable F se define
como el cociente entre dos
variables cuadradas
divididas por sus
correspondientes grados de
libertad.
Una variable con
distribución F es siempre
positiva por lo tanto su
campo de variación es 0 " F
La distribución de la variable es asimétrica,
pero su asimetría disminuye cuando
aumentan los grados de libertad del
numerador y denominador. Hay una
distribución F por cada par de grados de
libertad.

10. Distribución de Probabilidad
Cuadrada
Una variable
cuadrada se define
como la suma de n
variables normales
estandarizadas
elevadas al
cuadrado.
A medida que aumenta el
tamaño de la muestra la
curva es menos asimétrica,
aproximándose a una
curva normal.
El parámetro que caracteriza a una
distribución x 2 son sus grados de libertad (n-
1), originado una distribución para cada grado
de libertad.

11. Ejemplo:
Considerando nuevamente las
muestras aleatorias independientes de
distribuciones normales, sabemos que
    2
2
1   n 1 S / y  n 1 S /
2
2
2 2
2
2
2
1
2
1 1
2 
Tienen
distribuciones
 1  1 1 1 2 2 v  n  yv  n 
Así la definición
implica que
   

    2
2
2
2
2
1
2
1
n S n
 
1 / 1
F 
2

2
2
2
2 2
1
2
1
2
1 1
v
2

2
2
1
2
1
/
/
1 / 1
/
/



S
S
n S n
v
 
 

12. Distribución Gama
Este modelo es una generalización del modelo Exponencial ya que, en
ocasiones, se utiliza para modelar variables que describen el tiempo
hasta que se produce p veces un determinado suceso.
Como vemos, este modelo
depende de dos parámetros
positivos: α y p. La función Γ(p) es
la denominada función Gamma de
Euler que representa la siguiente
integral:
que verifica Γ(p + 1) =
pΓ(p), con lo que, si p es un
número entero positivo, Γ(p
+ 1) = p!

13. Esta distribución es una
de las más importantes
distribuciones de
variable discreta .
Otro de sus usos frecuentes es
la consideración límite de
procesos dicotómicos reiterados
un gran número de veces si la
probabilidad de obtener un éxito
es muy pequeña .
Sus principales aplicaciones hacen referencia
a la modelización de situaciones en las que
nos interesa determinar el número de hechos
de cierto tipo que se pueden producir en un
intervalo de tiempo o de espacio, bajo
presupuestos de aleatoriedad y ciertas
circunstancias restrictivas.

14. Ejemplo:
Un administrador de un hospital dice que existe un promedio de 3
emergencias por día ¿ cual es la probabilidad de que en un dia
dado ocurran 2 admisiones.
P(X): Probabilidad de tener exactamente por presentación.
e : 2,71828
X: Numero de presentaciones por unidades de tiempo.
Datos:
X= 3
X= 2 -3 2
P(2)= e (3)= 0,225
2!