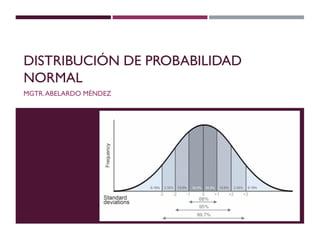
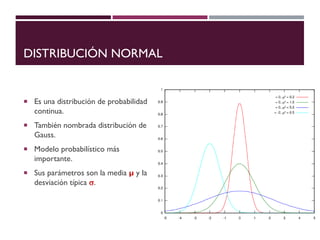
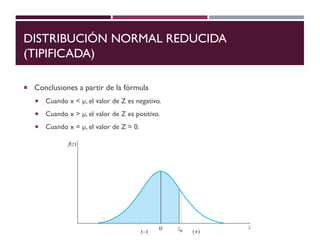
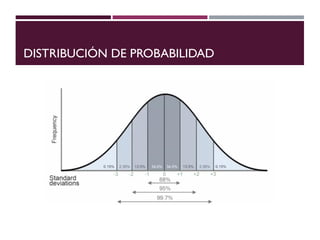
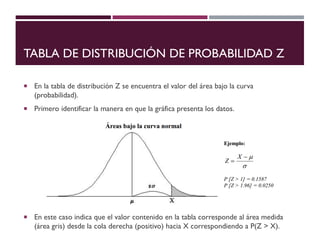
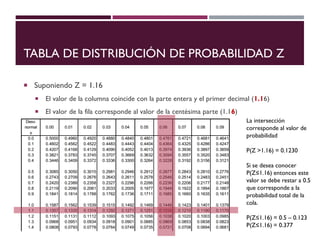
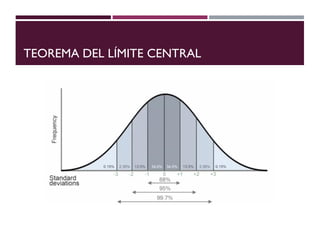
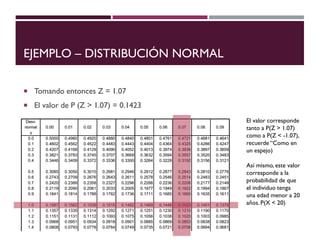
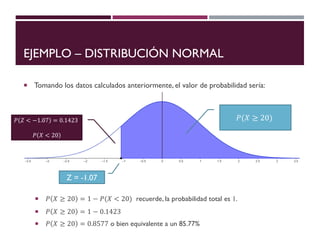
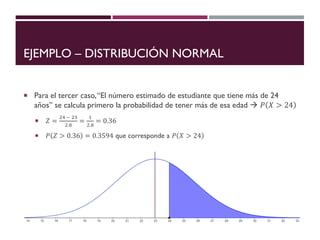
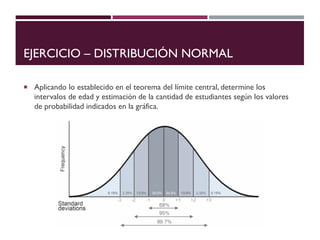
El documento describe la distribución de probabilidad normal, también conocida como distribución de Gauss, y sus características fundamentales como la media, moda y mediana que coinciden en el máximo de la curva. Se explica la distribución normal reducida, el cálculo del puntaje z, y se presentan ejemplos prácticos utilizando el teorema del límite central para determinar probabilidades en muestras de edad. Finalmente, se calcula la probabilidad de ciertos rangos de edad y el número estimado de estudiantes dentro de un grupo, ilustrando aplicaciones prácticas de la teoría.

1. DISTRIBUCIÓN DE PROBABILIDAD
NORMAL
MGTR.ABELARDO MÉNDEZ

2. DISTRIBUCIÓN NORMAL
 Es una distribución de probabilidad
continua.
 También nombrada distribución de
Gauss.
 Modelo probabilístico más
importante.
 Sus parámetros son la media µ y la
desviación típica .

3. CARACTERÍSTICAS
 Media, moda y mediana coinciden en el máximo de la curva
 El área encerrada bajo la campana y el eje x es igual a la unidad.
 Los puntos de inflexión son los puntos µ+ y µ- 

4. DISTRIBUCIÓN NORMAL REDUCIDA
(TIPIFICADA)
 Puntaje Z a partir de la variable X que sigue una distribución Normal.
 El área bajo la curva es la probabilidad de P(Z ≤ Z0)
 Parámetros → Distribución Normal Estandarizada
 Media µ = 0.
 Desviación típica  = 1.
 Puntos de inflexión en Z = ±1.
𝑍 =
𝑥 − 𝜇
𝜎
𝑍 =
𝑥 − ҧ𝑥
𝑠
𝑥 = 𝜇 + 𝜎. 𝑍
Z
µ

5. DISTRIBUCIÓN NORMAL REDUCIDA
(TIPIFICADA)
 Conclusiones a partir de la fórmula
 Cuando x < µ, el valor de Z es negativo.
 Cuando x > µ, el valor de Z es positivo.
 Cuando x = µ, el valor de Z = 0.

6. DISTRIBUCIÓN DE PROBABILIDAD

7. TABLA DE DISTRIBUCIÓN DE PROBABILIDAD Z
 En la tabla de distribución Z se encuentra el valor del área bajo la curva
(probabilidad).
 Primero identificar la manera en que la gráfica presenta los datos.
 En este caso indica que el valor contenido en la tabla corresponde al área medida
(área gris) desde la cola derecha (positivo) hacia X correspondiendo a P(Z > X).

8. TABLA DE DISTRIBUCIÓN DE PROBABILIDAD Z
 Suponiendo Z = 1.16
 El valor de la columna coincide con la parte entera y el primer decimal (1.16)
 El valor de la fila corresponde al valor de la centésima parte (1.16)
La intersección
corresponde al valor de
probabilidad
P(Z >1.16) = 0.1230
Si se desea conocer
P(Z≤1.16) entonces este
valor se debe restar a 0.5
que corresponde a la
probabilidad total de la
cola.
P(Z≤1.16) = 0.5 – 0.123
P(Z≤1.16) = 0.377

9. TEOREMA DEL LÍMITE CENTRAL
 Es fundamental de probabilidad y estadística.
 Describe la distribución de la media de una muestra aleatoria proveniente de
una población con varianza finita.
 Muestra suficientemente grande, la distribución de las medias sigue
aproximadamente una distribución normal.
 El tamaño de la muestra depende de la forma de la distribución original.
 Distribución simétrica → tamaño pequeño podría producir una aproximación
adecuada.
 Distribución considerablemente asimétrica → Tamaño de muestra más grande.
 Se aplica independientemente de la forma de la distribución de la población.

10. TEOREMA DEL LÍMITE CENTRAL
 Muestras de tamaño n de una población
 No importa la forma de la distribución original de la población, la distribución de
promedios seguirá una distribución normal.
 Útil para probar hipótesis
 Puede demostrar que la muestra representa a una población distinta de la conocida.
 La comprobación se hace directamente aplicando este teorema
 Si la probabilidad de observar que el promedio en estudio es mayor (o menor) es lo
suficientemente baja, entonces se puede rechazar la afirmación (hipótesis nula) de que
la muestra es como las otras.

11. TEOREMA DEL LÍMITE CENTRAL

12. EJEMPLO – DISTRIBUCIÓN NORMAL
 Suponga que un grupo de 80 estudiantes tiene una media de edad de 23 años
con desviación estándar de 2.8 años. Suponiendo que sigue una distribución
normal, calcule:
 La probabilidad de que un estudiante seleccionado al azar dentro de ese grupo tenga
por lo menos 20 años.
 La probabilidad de que un estudiante seleccionado al azar dentro del grupo, tenga
entre 22 y 25 años.
 El número estimado de estudiante que tiene más de 24 años.

13. EJEMPLO – DISTRIBUCIÓN NORMAL
 La probabilidad de que un estudiante seleccionado al azar dentro de ese grupo
tenga más de 20 años → 𝑃 𝑋 ≥ 20 que corresponde al área en color azul.
 50% de probabilidad acumulada en la mitad derecha (23 en adelante)
+
 La probabilidad contenida en el área bajo la curva desde X (20) hasta la media (23).

14. EJEMPLO – DISTRIBUCIÓN NORMAL
 Se procede a calcular el valor del puntaje Z que da la distancia medida desde la
media (23) hasta X (20) en términos de desviaciones estándar.
 𝑍 =
20 −23
2.8
=
−3
2.8
= −1.07
Z = -1.07

15. EJEMPLO – DISTRIBUCIÓN NORMAL
 Se debe tener en consideración que la tabla de distribución Z brinda el valor del
área bajo la curva (probabilidad) para valores positivos mayores que Z desde el
extremo izquierdo hacia la media.
 Sin embargo también debe recordar que la gráfica es simétrica por lo que se
debe identificar el área como si se tratara de su reflejo en un espejo.
 Sabiendo esto, el valor de probabilidad encontrado en la tabla se corresponde
con la probabilidad complementaria del problema en cuestión. (ver las imágenes
siguientes.

16. EJEMPLO – DISTRIBUCIÓN NORMAL
Z = -1.07
Probabilidad
que encontrará
en la tabla
Probabilidad
complementaria

17. EJEMPLO – DISTRIBUCIÓN NORMAL
 Tomando entonces Z = 1.07
 El valor de P (Z > 1.07) = 0.1423
El valor corresponde
tanto a P(Z > 1.07)
como a P(Z < -1.07),
recuerde “Como en
un espejo)
Así mismo, este valor
corresponde a la
probabilidad de que
el individuo tenga
una edad menor a 20
años. P(X < 20)

18. EJEMPLO – DISTRIBUCIÓN NORMAL
 Tomando los datos calculados anteriormente, el valor de probabilidad sería:
 𝑃 𝑋 ≥ 20 = 1 − 𝑃(𝑋 < 20) recuerde, la probabilidad total es .
 𝑃 𝑋 ≥ 20 = 1 − 0.1423
 𝑃 𝑋 ≥ 20 = 0.8577 o bien equivalente a un 85.77%
Z = -1.07
𝑃 𝑍 < −1.07 = 0.1423
𝑃 𝑋 < 20
𝑃(𝑋 ≥ 20)

19. EJEMPLO – DISTRIBUCIÓN NORMAL
 La probabilidad de que un estudiante seleccionado al azar dentro de ese grupo
tenga entre 22 y 25 años → 𝑃 22 ≤ 𝑋 ≤ 25 . Siempre es útil dibujar las
condiciones del problema.
𝑃 22 ≤ 𝑋 ≤ 25
𝑃 𝑋 > 25𝑃 𝑋 < 22

20. EJEMPLO – DISTRIBUCIÓN NORMAL
 Se procede a calcular los valores de Z para ambos extremos (entre 22 y 25).
 𝑍1 =
22 − 23
2.8
=
−1
2.8
= −0.36
 𝑍2 =
25 − 23
2.8
=
2
2.8
= 0.71
𝑍1 = −0.36 𝑍2 = 0.71

21. EJEMPLO – DISTRIBUCIÓN NORMAL
 Siguiendo la mecánica del problema anterior, las probabilidades complementarias
obtenidas en la tabla son:
 𝑃 𝑍1 < −0.36 = 0.3594 que corresponde a 𝑃 𝑋 < 22
 𝑃 𝑍2 > 0.71 = 0.2389 que corresponde a 𝑃 𝑋 > 25
 Por tanto, la probabilidad de que un estudiante seleccionado al azar dentro de
ese grupo tenga entre 22 y 25 años es:
 𝑃 22 ≤ 𝑋 ≤ 25 = 1 − 𝑃 𝑋 < 22 − 𝑃 𝑋 > 25
 𝑃 22 ≤ 𝑋 ≤ 25 = 1 − 0.3594 − 0.2389
 𝑃 22 ≤ 𝑋 ≤ 25 = 1 − 0.5983
 𝑃 22 ≤ 𝑋 ≤ 25 = 0.4017 lo cual es equivalente a un 40.17%

22. EJEMPLO – DISTRIBUCIÓN NORMAL
 Para el tercer caso,“El número estimado de estudiante que tiene más de 24
años” se calcula primero la probabilidad de tener más de esa edad → 𝑃 𝑋 > 24
 𝑍 =
24 − 23
2.8
=
1
2.8
= 0.36
 𝑃 𝑍 > 0.36 = 0.3594 que corresponde a 𝑃 𝑋 > 24

23. EJEMPLO – DISTRIBUCIÓN NORMAL
 Puesto que, como se explicó en clases anteriores, el valor de probabilidad se
corresponde con la frecuencia relativa, por tanto también es una proporción.
 Teniendo en cuenta que 𝑃 𝑋 > 24 = 0.3594 sería la proporción de estudiantes
mayores de 24 años.
 Entonces el número de estudiantes mayores de 24 años es:
 𝑀𝑎𝑦𝑜𝑟𝑒𝑠 𝑑𝑒 24 = 𝑁 ∗ 𝑃 𝑋 > 24
 𝑀𝑎𝑦𝑜𝑟𝑒𝑠 𝑑𝑒 24 = 80 ∗ 0.3594
 𝑀𝑎𝑦𝑜𝑟𝑒𝑠 𝑑𝑒 24 = 28.75 aproximadamente 29 estudiantes.

24. EJERCICIO – DISTRIBUCIÓN NORMAL
 Aplicando lo establecido en el teorema del límite central, determine los
intervalos de edad y estimación de la cantidad de estudiantes según los valores
de probabilidad indicados en la gráfica.

25. GRACIAS POR SU ATENCIÓN!!