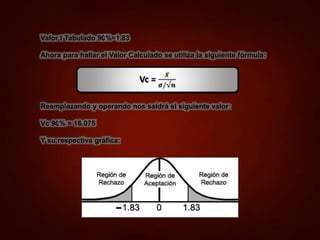
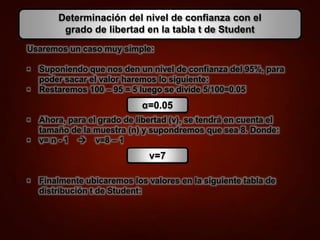
La distribución t de Student se aplica cuando la desviación típica poblacional es desconocida y la muestra es menor de 30, permitiendo establecer intervalos de confianza y realizar pruebas de hipótesis. Introducida por William S. Gosset, la distribución t presenta características distintas a la normal, especialmente en el área de sus extremos. Se explica cómo calcular intervalos de confianza utilizando la fórmula adecuada y se dan ejemplos prácticos con sus respectivos resultados.

2. Distribución T de Student
La distribución t de Student se
utiliza cuando nos encontramos
con la dificultad de no conocer la
desviación típica poblacional y
nuestra muestra es menor de 30.
Es similar a la curva normal, pero
la distribución t tiene mayor área
a los extremos y menos en el
centro.
Concepto y breve historia
Esta fue descubierta por un especialista en estadística de una
empresa irlandesa, este señor cuyo nombre era William S.
Gosset, hizo inferencias acerca de la media cuando la desviación
poblacional fuese desconocida; y ya que a los
empleados de dicha entidad no les era permitido publicar el
trabajo de investigación bajo sus propios nombres, Gosset
adoptó el seudónimo de “Student”.

3. Sus funciones se basan en establecer un intervalo de confianza,
utilizando un nivel de confianza y los grados de libertad,
obteniendo valores de una tabla dada con respecto a estas
variables y aplicarla en la formula.
De gran utilidad, reduce tiempo, costo y esfuerzos. Se utiliza para
probar hipótesis y también para saber si dos muestras provienen
de la misma población.
Grados de Libertad (V)
En la mayoría de los casos, los parámetros de una población son
cantidades desconocidas y para estimarlos es necesario extraer
una muestra de la población y calcular los estadísticos
correspondientes.
Existen varias distribuciones t. Cada una de ellas está asociada
con los que se denominan “Grados de libertad” (generalmente
denotado por la letra V), esté se define como el número de
valores que podemos elegir libremente, ósea, el número de
observaciones menos uno, ν = n – 1.

4. Nos interesa en nuestro caso particular poder establecer el
intervalo de confianza para estimar la media poblacional, para
ello haremos uso de la siguiente fórmula:
Fórmula general
μ= x̄ ± t(α, ν) *σ*n
Donde:
• μ = media poblacional.
• x̄ = media muestral (promedio).
• t(α, ν) = valor obtenido de la tabla de
la distribución “t”.
α = nivel de confianza.
ν = grados de libertad (v=n-1).
• σ = desviación estándar.
• n = tamaño de la muestra.

5. Usaremos un caso muy simple:
• Suponiendo que nos den un nivel de confianza del 95%, para
poder sacar el valor haremos lo siguiente:
• Restaremos 100 – 95 = 5 luego se divide 5/100=0.05
• Ahora, para el grado de libertad (v), se tendrá en cuenta el
tamaño de la muestra (n) y supondremos que sea 8. Donde:
• v= n - 1  v=8 – 1
• Finalmente ubicaremos los valores en la siguiente tabla de
distribución t de Student:
Determinación del nivel de confianza con el
grado de libertad en la tabla t de Student
α=0.05
v=7

6. Tabla t de Student
• Teniendo ya los dos valores, trataremos de ubicar en la tabla:
• Llegando a obtener un valor t(α, ν) de:
2.365
α=0.05 v=7
2.365

7. Ejercicio 01
• El auditor de una empresa al examinar los registros de
facturación mensual, mediante el análisis de una muestra
aleatoria irrestricta de 10 facturas no pagadas encontró que
la media aritmética fue de $9500 con una desviación
estándar de $327. Hallar el intervalo de confianza del 95%
para estimar el parámetro poblacional.
• Datos:
x̄ = 9500
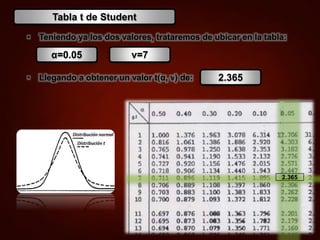
α = 0.05
ν = 9
σ = 327
n = 10
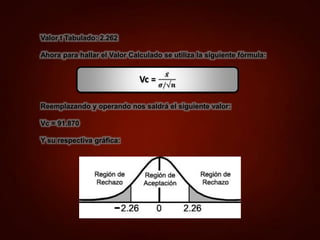
t(α, ν) =2.262
μ= 9500 ± 2.262 * 327 * 10
μ=[16896.74 ; 2103.26]
El intervalo de confianza para estimar el parámetro
poblacional está entre 16896.74 hasta 2103.26
μ= x̄ ± t(α, ν) *σ*n

8. Valor t Tabulado: 2.262
Ahora para hallar el Valor Calculado se utiliza la siguiente fórmula:
Reemplazando y operando nos saldrá el siguiente valor:
Vc = 91.870
Y su respectiva gráfica:
Vc =
𝒙̄
𝝈/√𝒏

9. Ejercicio 02
• Se realizó un estudio sobre la utilización del agua en una
pequeña ciudad. Para ello se considero una muestra de 25
casas. Teniendo como promedio un valor de 175.76 y una
desviación estándar de 20.79. Hallar el intervalo de
confianza del 90%para estimar el parámetro poblacional.
• Datos:
x̄ = 175.76
α = 0.1
ν = 24
σ = 20.79
n = 25
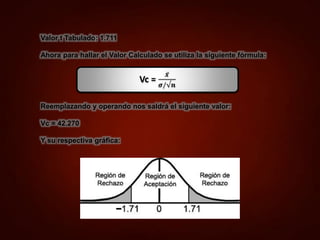
t(α, ν) =1.711
μ= 175.76 ± 1.711 * 20.79 * 25
μ=[1065.05 ; -713.53]
El intervalo de confianza para
estimar el parámetro
poblacional esta entre 1065.05
y -713.53
μ= x̄ ± t(α, ν) *σ*n

10. Valor t Tabulado: 1.711
Ahora para hallar el Valor Calculado se utiliza la siguiente fórmula:
Reemplazando y operando nos saldrá el siguiente valor:
Vc = 42.270
Y su respectiva gráfica:
Vc =
𝒙̄
𝝈/√𝒏

11. Ejercicio 03
• Se tienen las edades de 10 asegurados a una empresa que
tiene un x̄ =39.5 y una σ = 7.77. Hallar el intervalo de confianza
para el 90% y represente gráficamente
• Datos:
x̄ = 39.5
α (90%)= 0.1
ν = 9
σ = 7.77
n = 10
t(α 90%, ν) =1.83
μ= 39.5 ± 1.83 * 7.77 * 10
μ=[181.691 ; -102.691]
El intervalo de confianza para el 90% esta entre 181.691
hasta -102.691
μ= x̄ ± t(α, ν) *σ*n

12. Valor t Tabulado 90%=1.83
Ahora para hallar el Valor Calculado se utiliza la siguiente fórmula:
Reemplazando y operando nos saldrá el siguiente valor:
Vc 90% = 16.075
Y su respectiva gráfica:
Vc =
𝒙̄
𝝈/√𝒏