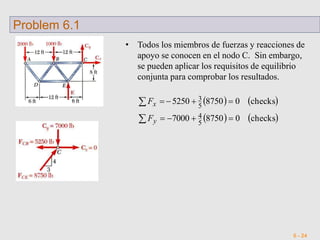
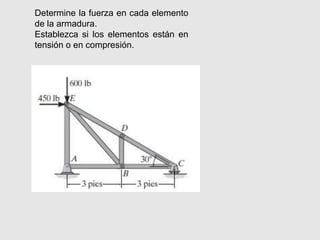
El documento presenta conceptos básicos sobre armaduras. Define una armadura como una estructura compuesta por miembros rectos conectados en empalmes, donde ningún miembro es continuo a través de una articulación. Explica que una armadura simple se construye agregando sucesivamente dos miembros y una conexión triangular básica. Además, introduce el método de nodos para el análisis de armaduras, el cual involucra crear un diagrama de cuerpo libre para cada miembro y perno y establecer ecuaciones de