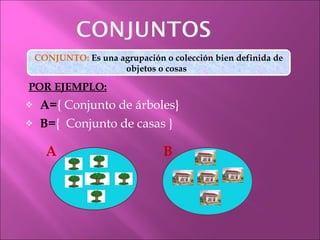
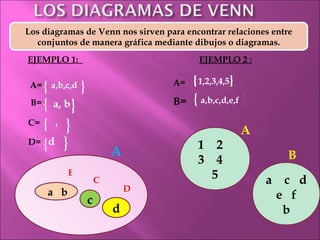
El documento resume los conceptos básicos de conjuntos, incluyendo conjuntos finitos e infinitos, el conjunto vacío, el conjunto universal, conjuntos potencia, conjuntos disjuntos, igualdad de conjuntos, subconjuntos y diagramas de Venn y lineales para representar relaciones entre conjuntos. Proporciona ejemplos de cada uno de estos conceptos.

2. CONCEPTO DE CONJUNTO CONJUNTO FINITO CONJUNTO INFINITO CONJUNTO VACIO CONJUNTO UNIVERSAL CONJUNTO POTENCIA CONJUNTOS DISJUNTOS IGUALDAD DE CONJUNTOS CONJUNTOS DE CONJUNTOS SUBCONJUNTOS DIAGRAMAS DE VENN- EULER DIAGRAMAS LINEALES MENSAJE

4. En este tipo de conjunto podemos contar sus elementos , es decir tienen un principio y un fin POR EJEMPLO : M= { } 4 Manzanas F= { } 6 Sillas

8. Es la familia de todos los subconjuntos de un conjunto N se llama Conjunto Potencia de N. Se le denota como 2 EJEMPLO 1: M = { 1, 2 } El conjunto M tiene 2 elementos 2 M = { {1}, {2}, {1, 2}, ø} entonces 2 2 = 4 elementos EJEMPLO 2: M = { 1, 2, 3 } El conjunto M tiene 3 elementos 2 M = { {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, ø} entonces 2 3 = 8 elementos

9. Son los conjuntos que tienen los mismos elementos sin importar su orden o repetición EJEMPLO 1: H= { } P= { } N= { 2,4,6,8,10,12 } M= { 4,8,2,12,4,10 } EJEMPLO 2: