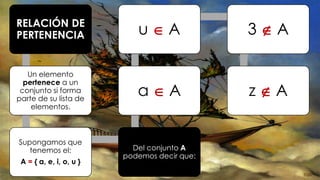
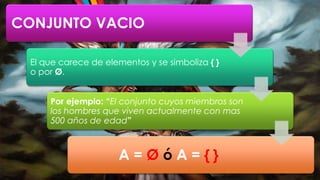
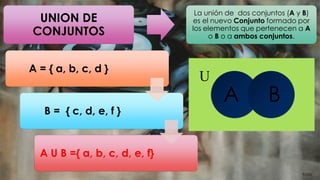
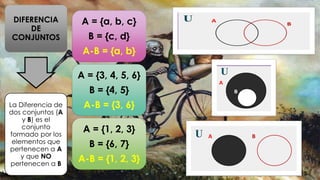
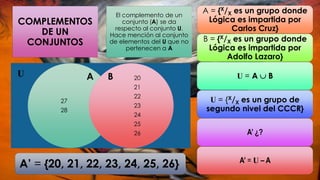
Este documento presenta una introducción a la teoría de conjuntos. Define lo que es un conjunto y cómo se pueden expresar explícita e implícitamente. Explica conceptos clave como pertenencia, igualdad, subconjunto, conjunto vacío, conjunto universal, unión, intersección y diferencia de conjuntos. También presenta el diagrama de Venn y los complementos de un conjunto.

1. Colegio Cervantes Costa Rica.
Asignatura: Lógica.
Profesor: Adolfo Lazaro Nava.
TEORÍA DE
CONJUNTOS o
TEORÍA DE CLASES
“Ningún problema puede ser resuelto en el mismo
nivel de conciencia en el que se creó” Albert
Einstein.

2. Conjunto es una colección de
objetos o entidades
distinguibles y bien definidas.
Los objetos (números, letras,
puntos, etc.) que constituyen
un conjunto se les llama
miembros o elementos del
conjunto.
Utilizaremos mayúsculas (A, B, X, Y,….)
para denotar Conjuntos.
Para denotar los elementos utilizaremos
minúsculas (a,b,c,…), números,
símbolos, variables, etc.

3. FORMAS DE EXPRESAR UN CONJUNTO
EXPLÍCITAMENTE
(extensión)
Escribir cada elemento que componen
el conjunto dentro de llaves y
separados por una coma
A = { a, e, i, o, u }
B = {lunes, martes, miércoles,
jueves, viernes, sábado, domingo}
IMPLÍCITAMENTE
(comprehensión)
Escribir dentro de las llaves las
características de los elementos que
pertenecen al conjunto.
A = {x/x es una vocal}
B = {x/x es un día de la semana}

4. SÍMBOLO O FORMULA TRADUCCIÓN
 Pertenece a…
 NO pertenece a…
 
Simboliza una clase que puede estar determinada por el
método de la extensión o de la comprehensión: “la clase
cuyos individuos son...”.
x Individuo o elemento cualquiera.
A, B, etc. (mayúsculas) Expresa un conjunto.
Minúsculas Expresa elementos.
 Intersección.
 Unión.
A’
Complemento de A
(la clase formada por los elementos que no pertenecen a A).
 Subconjunto de…
 NO es subconjunto de…
{ } o Ø Conjunto vacío.
U Conjunto universal.
= Relación de igualdad.

5. RELACIÓN DE
PERTENENCIA
Un elemento
pertenece a un
conjunto si forma
parte de su lista de
elementos.
Supongamos que
tenemos el:
A = { a, e, i, o, u }
Del conjunto A
podemos decir que:
a  A
u  A 3  A
z  A

6. Implica que si x є A, entonces también x є B y
si y є B, entonces también y є A
A = {x, y} B = {y, x}
A = B
IGUALDAD DE CONJUNTOS
Decimos que dos conjuntos (A y B)son iguales (A = B ) si todos
los elementos de A pertenecen a B

7. SUBCONJUNTO
Cuando todos y cada uno
de los elementos de un
conjunto (A) son también
elementos de otro
conjunto (B), entonces A es
Subconjunto de B (A esta
contenido en B).
A NO sería Subconjunto de
B, si por lo menos un
elemento de A no
pertenece a B.
A = { 1, 3, 4, 5, 8, 9 }
B = { 1, 2, 3, 5, 7 }
C = { 1, 5 }
De los anteriores conjuntos podemos
decir que:
C  A
C  B
B  A

8. CONJUNTO VACIO
El que carece de elementos y se simboliza { }
o por Ø.
Por ejemplo: “El conjunto cuyos miembros son
los hombres que viven actualmente con mas
500 años de edad”
A = Ø ó A = { }

9. CONJUNTO
UNIVERSAL
Género que
pueden tener los
conjuntos en tanto
que especies.
A = {1, 2, 3, 4, 5}
B = {x/x es un numero primo}
C = {x/x es un numero natural par}
A, B y C son subconjuntos propios del U (U es igual a
los N)

10. DIAGRAMA DE VENN
Si A={ 1, 2, 3,} B= { 1 } C={ 8,9 } D={ 8}
U
A
B
C
D
A U C UB U D U
B A D C

11. UNION DE
CONJUNTOS
La unión de dos conjuntos (A y B)
es el nuevo Conjunto formado por
los elementos que pertenecen a A
o B o a ambos conjuntos.
A = { a, b, c, d }
B = { c, d, e, f }
A U B ={ a, b, c, d, e, f}
A B
U

12. INTERSECCION DE
CONJUNTOS
La intersección de dos conjuntos
(A y B) da el nuevo conjunto
formado por los elementos
comunes a ambos conjuntos
A={a, b, c, d}
B= {c, d, e, f}
A ∩ B = { c, d }
A B
U A
B
U
A={ a, b, c, d }
B= { c, d }
A ∩ B = { c, d }
A B
U
A={a, b, c, d}
B= {m, p, q}
A ∩ B = Ø

13. DIFERENCIA
DE
CONJUNTOS
La Diferencia de
dos conjuntos (A
y B) es el
conjunto
formado por los
elementos que
pertenecen a A
y que NO
pertenecen a B
A = {a, b, c}
B = {c, d}
A-B = {a, b}
A = {3, 4, 5, 6}
B = {4, 5}
A-B = {3, 6}
A = {1, 2, 3}
B = {6, 7}
A-B = {1, 2, 3}

14. COMPLEMENTOS
DE UN
CONJUNTOS
El complemento de un
conjunto (A) se da
respecto al conjunto U.
Hace mención al conjunto
de elementos del U que no
pertenecen a A
A = {X/X es un grupo donde
Lógica es impartida por
Carlos Cruz}
B = {X/X es un grupo donde
Lógica es impartida por
Adolfo Lazaro}
U = A  B
U = {X/X es un grupo de
segundo nivel del CCCR}
A’ ¿?
A’ = U – A
27
28
20
21
22
23
24
25
26
U A B
A’ = {20, 21, 22, 23, 24, 25, 26}

15. Actividad 16
REALIZAR LOS EJERCICIOS
QUE ENTEGÓ EL DOCENTE.