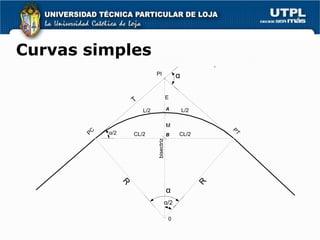
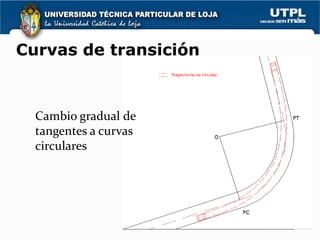
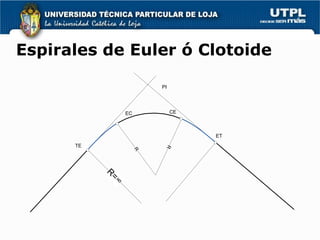
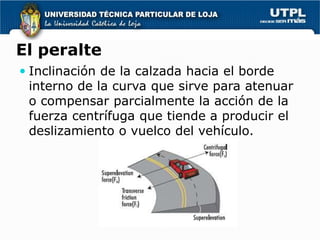
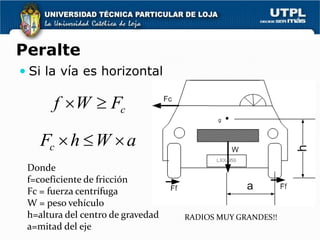
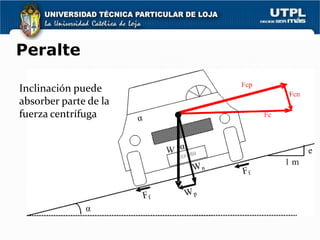
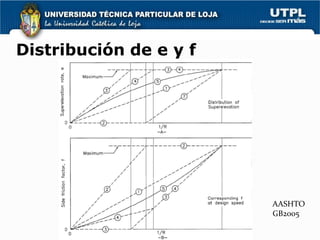
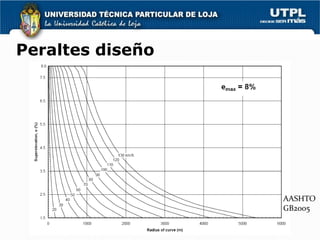
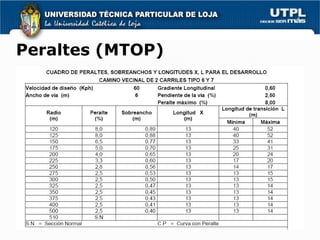
Este documento resume conceptos clave sobre el diseño en planta de vías, incluyendo: 1) El diseño en planta consta de una serie de tramos rectos unidos por curvas horizontales que permiten cambiar la alineación. 2) Las curvas pueden ser circulares simples o compuestas de una curva circular y dos curvas de transición (espirales) para una transición suave. 3) El peralte es la inclinación de la calzada hacia el interior de la curva para compensar parcialmente la fuerza centrífuga y depende

1. VIAS
Escuela: Ingeniería Civil
Instructor: Juan Pablo Solórzano Ing. Civil
MSc. Ingeniería y planificación de transportes
Fecha: Octubre - 2008

2. Semana 6

3. Capítulos 13-14

4. Diseño en planta
 Proyección sobre el plano horizontal del
eje real o espacial de la carretera
 Constituido por una serie de tramos rectos
(tangentes), enlazados entre si por curvas

5. Curvas horizontales
 Vincular en planta dos alineamientos
(tangentes) que forman un cierto ángulo
horizontal entre sí permitiendo desarrollar
progresivamente las fuerzas centrífugas y
desarrollar el peralte para compensarlas
parcialmente.
 Curvas circulares simples ó
 curva circular y dos curvas de transición
(espirales) a la entrada y salida.

6. El peralte
 Inclinación de la calzada hacia el borde
interno de la curva que sirve para atenuar
o compensar parcialmente la acción de la
fuerza centrífuga que tiende a producir el
deslizamiento o vuelco del vehículo.

7. Peralte
 Si la vía es horizontal
f W  Fc
Fc  h  W  a
Donde
f=coeficiente de fricción
Fc = fuerza centrífuga
W = peso vehículo
h=altura del centro de gravedad RADIOS MUY GRANDES!!
a=mitad del eje

8. Peralte
Inclinación puede
absorber parte de la
fuerza centrífuga

9. Peralte
WV 2
W sin   fN  cos 
gR
 WV 2
 WV 2
W sin   f W cos  
 sin   
 cos 
 gR  gR
 V2  V2
tg    f 1 
 gR tg    gR

 

10. Peralte
V2
tg    f 1  0 
gR
V2 V2
R 
g e  f  127e  f 
V2
e f
127 R

11. Selección de e y f
 Límites prácticos del peralte (e)
 Clima
 Construcción
 Uso del suelo adyacente
 Vehículos pesados (lentos)
 Variaciones en el coeficiente de fricción
lateral (f)
 Velocidad del vehículo
 Textura del pavimento
 Condiciones de los neumáticos

12. Coeficientes de fricción Vías de velocidad alta

13. Coeficientes de fricción Vías de velocidad baja

14. Coeficientes AASHTO GB2005
AASHTO
GB2005

15. Distribución de e y f
5 métodos de “sostener” la fuerza centrífuga
usando e ó f, o ambas
 1. Peralte y fricción lateral son
directamente proporcionales al inverso del
radio
 2. La fricción es tal que un vehículo que
viaja a la velocidad de diseño, toda la
aceleración lateral es soportada por la
fricción en curvas de hasta fmax. Para
curvas mas cerradas fmax se mantiene y e
aumenta para soportar la fuerza lateral
hasta emax

16. Distribución de e y f
 3. El peralte es tal que un vehículo que
viaja a la velocidad de diseño, toda la
aceleración lateral es soportada por el
peralte hasta emax. Para curvas mas
cerradas emax se mantiene y f aumenta
para soportar la fuerza lateral hasta fmax
 4. Igual que 3 pero con velocidad de
operación
 5. Relación curvilínea entre métodos 1 y 3

17. Distribución de e y f
AASHTO
GB2005

18. Peraltes máximos
 10 % en carreteras
 12 % límite práctico (AASHTO)
 8% caminos lastrados
 8% máximo cuando hay hielo / nieve
 4-6% zonas urbanas

19. Peraltes diseño
AASHTO
GB2005

20. V2
Radio mínimo Rmin 
127emax  f max 

21. Peraltes (MTOP)

23. Tipos
 Simples
 Un solo radio que une dos tangentes
 Curvas espirales de transición
 Comodidad
 Espirales de Euler (clotoide)
 Curvas compuestas
 Varias curvas conectadas
 Curvas del mismo sentido
 Evitar
 Curvas reversas
 Se requiere de separación suficiente
(peralte)

24. Curvas simples
PI α
E
T
L/2 A L/2
M
α/2
PC
PT
CL/2 B CL/2
bisectriz
R
R
α
α/2
0

25. Curvas simples
 PIPunto intersección tangentes principales
 PC punto de inicio de curva (tangencia)
 PT Inicio de tangente (fin de curva)
 O Centro curva circular
 α ángulo de deflexión de las tangentes (igual ángulo
central
 R radio de la curva simple
 T tangente (subtangente) PI a PC o PI a PT
 L longitud curva circular (PC a PT)
 CL cuerda larga, distancia recta PC a PT
 E external desde PI al centro de la curva
 M ordenada media, del punto A a B

26. Expresiones curvas

T  R tan
2

L R
180
 1 
E  R
 cos 2  1

 
  Cálculo de abscisado
M  R1  cos 
 2 PT  PC  L

27. Curvas de transición
Cambio gradual de
tangentes a curvas
circulares

28. Curvas de transición
 Provee una ruta natural y de facil
seguimiento para los conductores,
promueve velocidades uniformes,
incremento gradual de las fuerzas
laterales
 Provee una longitud de transición para el
desarrollo del peralte
 Provee una longitud de transición para el
ensanchamiento
 Estética

29. Espirales de Euler ó Clotoide
PI
EC CE
ET
TE
R
R
R
=∞

30. Espirales de Euler ó Clotoide
 PI Punto intersección tangentes
principales
 TE Tangente – espiral (inicio espiral)
 EC Espiral-circular (inicio circular)
 CE Circular – Espiral (inicio espiral de
salida)
 ET Espiral tangente (final espiral de salida)
 R radio de la curva central

31. Espirales de Euler ó Clotoide
 Consultar fórmulas