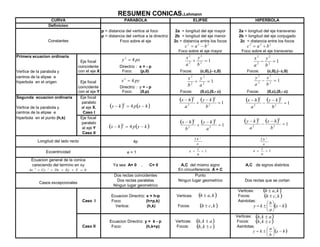
El documento detalla las definiciones y propiedades de las cónicas, incluyendo la parábola, elíptica e hiperbólica. Se presentan fórmulas para calcular distancias entre focos, vértices y directrices, así como ecuaciones ordinarias vinculadas a cada tipo de cónica. También se discuten casos especiales y la representación gráfica de estas curvas.

1. RESUMEN CONICAS.Lehmann
CURVA PARABOLA ELIPSE HIPERBOLA
Definicion
p = distancia del vertice al foco 2a = longitud del eje mayor 2a = longitud del eje transverso
p = distancia del vertice a la directriz 2b = longitud del eje menor 2b = longitud del eje conjugado
Constantes Foco sobre el eje 2c = distancia entre los focos 2c = distancia entre los focos
c2  a2  b2 c2  a2  b2
Foco sobre el eje mayor Foco sobre el eje transverso
Primera ecuacion ordinaria x 2
y 2
x2 y2
Eje focal y 2  4 px  2 1  1
2
coincidente Directriz : x = - p
a b a2 b2
Vertice de la parabola y con el eje X Foco: (p,0) Focos: (c,0),(- c,0) Focos: (c,0),(- c,0)
2
centros de la elipse e x2 y2 y x2
hiperbola en el origen Eje focal x 2  4 py  2 1  2 1
b2 a a2 b
coincidente Directriz : y = - p
con el eje Y Foco: (0,p) Focos: (0,c),(0,- c) Focos: (0,c),(0,- c)
Segunda ecuacion ordinaria Eje focal
paralelo
x  h 2  y  k 2 1
x  h 2  y  k 2 1
Vertice de la parabola y al eje X. y  k 2  4 p x  h  a2 b2 a2 b2
centros de la elipse e Caso I
hiperbola en el punto (h,k) Eje focal
paralelo x  h 2 y  k 2 y  k 2  x  h 2 1
x  h 2
 4 p y  k   1
al eje Y b2 a2 a2 b2
Caso II
2 2
2b 2b
Longitud del lado recto 4p
a a
c c
Excentricidad e=1 e  1 e  1
a a
Ecuacion general de la conica
careciendo del termino en xy Ya sea A= 0 , C= 0 A,C del mismo signo A,C de signos distintos
Ax 2
 Cy 2
 Dx  Ey  F  0 En circunferencia A = C
Dos rectas coincidentes Punto
Dos rectas paralelas Ningun lugar geometrico Dos rectas que se cortan
Casos excepcionales
Ningun lugar geometrico
Vertices: h  a , k 
Ecuacion Directriz: x = h-p Vertices: h  a , k  Focos: h  c , k 
Caso I Foco: (h+p,k) Asintotas:
b
Vertice: (h,k) Focos: h  c , k  y  k   x  h 
a
Vertices: h , k  a 
Ecuacion Directriz: y = k - p Vertices: h, k  a  Focos: h , k  c 
Caso II Foco: (h,k+p) Focos: h , k  c  Asintotas:
a
y  k    x  h 
b