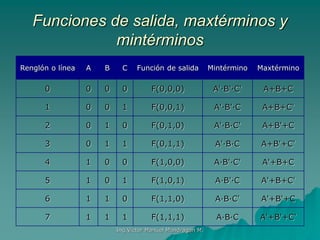
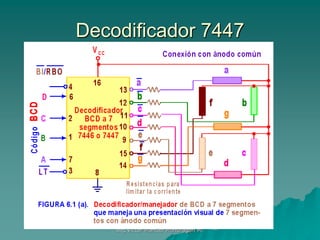
Este documento presenta información sobre diseño de circuitos lógicos combinatorios. Explica que un circuito combinacional es aquel cuyas salidas dependen exclusivamente de las entradas en un instante dado. Describe procedimientos de diseño como construir la tabla de verdad, aplicar sumas de productos y simplificar. Incluye ejemplos de diseño de sumadores, decodificadores y uso del método de mapas de Karnaugh para simplificar funciones lógicas.

1. Ing. Vitor Manuel Mondragon M
DISEÑO DE CIRCUITOS
COMBINATORIOS

2. Ing.Victor Manuel Mondragon M.
ANÁLISIS DE CIRCUITOS
COMBINACIONALES
 Un circuito combinacional es un
circuito digital cuyas salidas, en un
instante determinado y sin
considerar los tiempos de
propagación de las puertas, son
función, exclusivamente, de la
“combinación” de valores binarios de
las entradas del circuito en ese
mismo instante.

3. Ing.Victor Manuel Mondragon M.
Diseño de Circuitos Lógicos
Combinatorios
 Requerimiento
 Se construye la tabla de Verdad.
 NO siembre se aplica BOOLE y
DEMORGAN
 Aplicar Sumas de Productos.
 Simplificación con los teoremas
anteriores

4. Ing.Victor Manuel Mondragon M.
En que consiste?
Síntesis se entiende como la
obtención de circuitos lógicos,
a partir de una descripción
inicial que utiliza el lenguaje
convencional y luego es
transferida a una tabla de
verdad.

5. Ing.Victor Manuel Mondragon M.
Funciones de salida, maxtérminos y
mintérminos
Renglón o línea A B C Función de salida Mintérmino Maxtérmino
0 0 0 0 F(0,0,0) A'·B'·C' A+B+C
1 0 0 1 F(0,0,1) A'·B'·C A+B+C'
2 0 1 0 F(0,1,0) A'·B·C' A+B'+C
3 0 1 1 F(0,1,1) A'·B·C A+B'+C'
4 1 0 0 F(1,0,0) A·B'·C' A'+B+C
5 1 0 1 F(1,0,1) A·B'·C A'+B+C'
6 1 1 0 F(1,1,0) A·B·C' A'+B'+C
7 1 1 1 F(1,1,1) A·B·C A'+B'+C'

6. Ing.Victor Manuel Mondragon M.
Procedimientos de Diseño
Requerimiento
Diseñe un circuito lógico
que tenga entradas A, B y
C y cuya salida sea alta
solo cuando la mayor parte
de las entradas sean
ALTAS.

7. Ing.Victor Manuel Mondragon M.
Tabla de Verdad.
A B C X
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1

8. Ing.Victor Manuel Mondragon M.
Simplificación
 Se escriben los términos, para los
casos en que la salida es “UNO” y
se procede a simplificar
AB
AC
BC
X
C
C
AB
B
B
AC
A
A
BC
X
ABC
C
AB
ABC
C
B
A
ABC
BC
A
X
ABC
C
AB
ABC
C
B
A
ABC
BC
A
X
ABC
C
AB
C
B
A
BC
A
X

























)
(
)
(
)
(
)
(
)
(
)
(

9. Ing.Victor Manuel Mondragon M.
Implantación de Diseño Final.
1
2
3
4
5
6
9
10
8
1
2
13
12
U2:A
74AS27
A
B
C 1 2

10. Ing.Victor Manuel Mondragon M.
Ejemplo 2
 Se desea diseñar un sistema de aviso
muy simple para un coche,que debe
operar del siguiente modo:
– Si el motor está apagado y las puertas
abiertas, sonará una alarma.
– Si el motor está encendido y el freno de
mano está puesto,también sonará la
alarma.
– Las situaciones reales, motor encendido
o apagado, puertas abiertas o cerradas,
etc pueden tratarse como variables
binarias.

11. Ing.Victor Manuel Mondragon M.
Análisis
Sean f,e,p tres variables binarias que
indican:
 F freno de mano. Toma el valor 1 si está
puesto y 0 en caso contrario.
 P Puerta. Toma el valor 1 si alguna de
las puertas del coche están abiertas y 0
cuando todas las puertas están cerradas.
 e encendido. Toma el valor 1 si el motor
está arrancado, 0 si está apagado.
 La salida A puede considerarse también
como una señal binaria, A, que toma dos
valores posibles: Si A=1 , la alarma se
activa, si A=0, la alarma no se activa.

12. Ing.Victor Manuel Mondragon M.
Tabla de verdad
1
2
13
12
3
4
5
6
9
10
11
8
U2
NOT
f
p
e
U3
NOT
U4
NOT
1
2
13
12
U6
OR
U7
OR
U8
OR
A

13. Ing.Victor Manuel Mondragon M.
Diseñar un Sumador
Requerimiento
 Diseñar un Circuito Sumador de dos Bits
que produzca dos salidas S La suma y
C  un bit de transporte o
desbordamiento.
Tabla de Verdad
A B S T
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1

14. Ing.Victor Manuel Mondragon M.
Expresiones Lógicas
U1
XOR
U2
AND
0
0
A
B
S
C
S = A’ B + A B’
T= A B
0
0
A
B
OR

15. Ing.Victor Manuel Mondragon M.
Ejercicios
 Diseñar un Sumador de Tres BITS
 Diseñar un circuito lógico de 3 bits
cuya salida sea 1 solo cuando las
entradas ABC (ALSB, CMSB)
esten en un rango ente 4 y 8 binarior
espectivamente.
 Diseñar un decodificador de BCD a 7
Segmentos.

16. Ing.Victor Manuel Mondragon M.
Sumador de Tres Bits

17. Ing.Victor Manuel Mondragon M.
Generalización de Sumadores

18. Ing.Victor Manuel Mondragon M.
7 Segmentos
ANODO COMUN
CATODO COMUN

19. Ing.Victor Manuel Mondragon M.
Decodificador 7447

20. Ing.Victor Manuel Mondragon M.

21. Ing. Vitor Manuel Mondragon M
MÉTODO DE LOS
MAPAS DE
KARNAUGH

22. Ing.Victor Manuel Mondragon M.
Construcción de los Mapas de
KARNAUGH
 extensión del diagrama de Venn.
 Esto nace de la representación
geométrica de los números
binarios.
 Un número binario de n bits, puede
representarse por lo que se
denomina un punto en un espacio
N
 Numero de 1 bit  0 y 1

23. Ing.Victor Manuel Mondragon M.
CUBO 1. Representación de 1 bit
Cubo 0 Cubo 1
El cubo 1 se obtiene proyectando el cubo 0
0 1
Cubo 2
0 1
0 1
Cubo 2
00 01
10 11
El cubo 2 se obtiene proyectando el cubo 1

24. Ing.Victor Manuel Mondragon M.
1 Crear el mapa de Karnaug
 Recomendado para Máximo 6 Variables.
 Método de Simplificación Manual
 Se construye el mapa de Karnaugh

25. Ing.Victor Manuel Mondragon M.
Representación de 3 Variables

26. Ing.Victor Manuel Mondragon M.
Mapa de 3 y 4 Variables

27. Ing.Victor Manuel Mondragon M.
2- Fijar los 1 de las expresiones
z= A’B’C + A’BC
z=A’B’C’D’ + A’B’C’D+A’B’CD+A’B’CD’
+AB’C’D’+AB’CD+AB’CD’

28. Ing.Victor Manuel Mondragon M.
3 – Simplificación (1)
Z= AB’+AB=A Z=A’B + AB = B
Z=A’B’+A’B = A’ Z=A’B’+AB’= B’

29. Ing.Victor Manuel Mondragon M.
3- Simplificación(2)
 Para tres Variables.
Z= A’B’C’ + AB’C’ + ABC + ABC’
Z= (A’+A)B’C ‘+ AB(C+C’)
Z=B’C’ + AB

30. Ing.Victor Manuel Mondragon M.
3- Simplificación(3)
Z=A’B’C’+A’BC’ = A’C’ Z= AB’C’ + ABC’ = AC’

31. Ing.Victor Manuel Mondragon M.
3 – Variables Casos

32. Ing.Victor Manuel Mondragon M.
Cuando una variable aparece en forma
complementada (X’) y no
complementada (X) dentro de un
agrupamiento, esa variable se elimina
de la expresión. Las variables que son
iguales en todos agrupamientos
deben aparecer al final de la
expresión.
Conclusión

33. Ing.Victor Manuel Mondragon M.
4 Variables Caso 1

34. Ing.Victor Manuel Mondragon M.
4 Variables Bloques

35. Ing.Victor Manuel Mondragon M.
4 Variables Casos Varios
Alternativas ?

36. Ing.Victor Manuel Mondragon M.
4 Variables Casos Varios(2)

37. Ing.Victor Manuel Mondragon M.
Condición No Importa
C' C
A'B' 0 0
A'B 0 X
AB 1 1
AB' X 1
C' C
A'B' 0 0
A'B 0 0
AB 1 1
AB' 1 1
A B C Z
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 X
1 0 0 X
1 0 1 1
1 1 0 1
1 1 1 1
Z=A

38. Ing.Victor Manuel Mondragon M.
Resumen
1.- Dibujar la cuadrícula correspondiente al
número de variables de la función
2.- Sombrear la zona correspondiente a la
función (1)
3.- Recubrir dicha zona con bloques que sean
lo mayores posible
4.- Si se puede quitar algún bloque de forma
que la zona cubierta siga siendo la misma
5.- La expresión simplificada de f se
corresponde a la suma de los monomios
correspondientes a los bloques que queden

39. Ing. Vitor Manuel Mondragon M
Ejemplos
Mapas de Karnaugh

40. Ing.Victor Manuel Mondragon M.
Ejemplo 1
 Diseñar un circuito
lógico
combinatorio que
detecte, mediante
UNOS, los números
pares para una
combinación de 3
variables de
entrada.
DEC A B C Z
0
1
2
3
4
5
6
7
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
1
0
1
0
1
0
Función canónica

41. Ing.Victor Manuel Mondragon M.
Ejemplo 1 Solución
A'BC' + ABC' = (A' + A)BC' = BC'
A 0 0 0 1 1 1 1 0
0 0 0 0 1
1 1 0 0 1
BC

42. Ing.Victor Manuel Mondragon M.
Ejemplo 2- Circuito Velocímetro
 Se tienen 3 Códigos del ADC ABCD
 Las lámparas deben incrementarse de dos
niveles en dos.
 L1 ON  001
 L1 & L2 001 y 010 etc
 Los codigo 110 y 111 no responde.

43. Ing.Victor Manuel Mondragon M.
Solución

44. Ing.Victor Manuel Mondragon M.
Solución

45. Ing.Victor Manuel Mondragon M.
Ejemplo 3
 Diseñar un codificador de 4 a 2
líneas.
 Diseñar este mismo codificador pero
con prioridad.
 Diseñar un codificador de 8 a 3
líneas.
 Diseñar este mismo codificador pero
con prioridad.

46. Ing.Victor Manuel Mondragon M.
Ejemplo4
 Desarrollar un circuito Hardware de
3 bits para la función:
2
2
)
,
( Y
X
Y
X
f 

n
F(X,Y)
X
Y