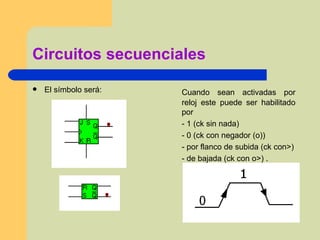
Este documento describe conceptos básicos de electrónica digital como señales analógicas y digitales, códigos de numeración como binario y hexadecimal, operaciones lógicas como AND, OR y NOT, y circuitos lógicos como codificadores, decodificadores y multiplexores. También explica cómo simplificar funciones lógicas usando álgebra de Boole y tablas de Karnaugh.

1. Electrónica Digital Tecnología industrial II Antonio Vives

2. Analógico y Digital Definición: Una señal analógica es aquella que puede tomar cualquier valor en el tiempo. Una señal digital es aquella que solo puede tomar dos valores; “valor alto” o “valor bajo”.

3. Códigos de Numeración Definición: Son formas de contar elementos con diferentes símbolos, normalmente empleamos el decimal. Decimal: emplea 10 símbolos: 0, 1,2, 3, 4, 5, 6, 7, 8, 9 Binario : emplea 2 símbolos: 0, 1 Octal: Emplea 8 símbolos 0, 1, 2, 3, 4, 5, 6, 7 Hexadecimal : Emplea 16 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1111 15 F 111 0 14 E 11 0 1 13 D 11 00 12 C 1 0 11 11 B 1 0 1 0 10 A 1 00 1 9 9 1 000 8 8 0 111 7 7 0 11 0 6 6 0 1 0 1 5 5 0 1 00 4 4 00 11 3 3 00 1 0 2 2 000 1 1 1 0000 0 0 Binario D ecimal Hexadecimal

4. Cambio de código Para cambiar de código decimal a cualquier código dividimos el valor decimal entre el número de elementos de ese códigos y después leemos desde el último cociente hasta el primer resto en ese orden y ese será el valor en el código correspondiente .

5. Cambio de código Para cambiar de cualquier código a decimal multiplicaremos cada bit del código correspondiente por el peso del bit en su código y después se suma el valor que tenga cada uno de lo bits El número 11010 en base 2 es: 0 x2 0 + 1 x2 1 0 x2 2 + + 1 x2 3 + 1 x2 4 = 16 + 8 + 0 + 2 + 0 = 26 en decimal El número 3A1 en base 16 es: 1 x16 0 + (A) 10 x16 1 + 3 x16 2 = 768 + 160 + 1 = 929 en decimal

6. Cambio de código Para cambiar de Binario a hexadecimal podemos agrupar el numero binario de 4 en 4 bits y poner el equivalente de cada grupo en hexadecimal y viceversa El número 11010 en base 2 es: 0001 = 1 y 1010 = A luego el equivalente en hexadecimal será 1A El número 3A1 en base 16 es: 3 =0011 , la 16 2 + A =1010 y el 1 =0001 luego en binario será: 001110100001

7. Operaciones lógicas básicas Suma lógica ; Función OR Producto lógico ;Función AND 1 1 1 1 1 0 1 0 1 0 0 0 S = A+B A B 1 1 1 0 1 0 0 0 1 0 0 0 S = A·B A B

8. Operaciones lógicas básicas Suma lógica negada Función NOR Producto lógico negado Función NAND 0 1 1 0 1 0 0 0 1 1 0 0 A B 0 1 1 1 1 0 1 0 1 1 0 0 A B

9. Operaciones lógicas básicas Inversor ; Función NOT Suma exclusiva Función EOR 0 1 1 0 A 0 1 1 1 1 0 1 0 1 0 0 0 A B

10. Configuración de las puertas lógicas

11. Configuración de las puertas lógicas

12. Propiedades del álgebra de Boole 1 ) Conmutativa a+b = b+a a·b = b·a 2 ) Asociativa a+b+c = a+(b+c) a·b·c = a·(b·c) 3 ) Distributiva a·(b+c) = a·b + a.c a+(b·c) = (a+b)·(a+c) ¡ojo! 4 ) Elemento neutro a+0 = a a·1 = a 5 ) Elemento absorbente a+1 = 1 a·0 = 0 6 ) Ley del complementario a+ā = 1 a·ā = 0 7 ) Idempotente a+a = a a·a = a 8 ) Simplificativa a+a·b = a a·(a+b) = a 9 ) Teoremas de De Morgan

13. Funciones lógicas y tabla de verdad Los circuitos digitales pueden venir representados por: Función lógica: Es la ecuación que da respuesta al problema Tabla de verdad: En una tabal se representan todos las posibles combinaciones de entrada y cual es la salida del sistema Circuito eléctrico-electrónico correspondiente: mediante puertas lógicas o contactos eléctricos se representa el funcionamiento del sistema 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 S c b a

14. Funciones lógicas y tabla de verdad A partir de función lógica se puede obtener la tabla de la verdad y viceversa. La función lógica puede ser simplificada o puede venir dada de forma especial. Formas canónicas. Miniterms: Es una suma de productos de todos los terminos que dan 1 en la tabla de verdad. (las variables se ponen normal) Maxiterms: Es un producto de todas la sumas que dan cero en la tabla de verdad. (Las variables se ponen negadas) 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 S c b a

15. Simplificación de funciones Las funciones se pueden simplificar Empleando el algebra de Boole Utilizando las propiedades y teoremas vistos anteriormente (Mas complicado y menos preciso) Utilizando los mapas (tablas) de Karnaugh. (Mas sencillo y asegura la máxima simplificación)

16. Simplificación empleando el algebra de Boole Dada la siguiente función lógica: Empleando la Propiedad Distributiva , agrupamos términos en parejas con el mayor número posible de variables iguales. Ley del complementario Elemento neutro

17. Tablas de Karnaugh Consiste en representar la tabla de verdad en una cuadricula de manera especial y de forma que se den todas las combinaciones posibles de la tabla de la verdad. Este método se puede emplear para funciones de hasta 5 variables de entrada. Una vez representada la tabla de Karnaugh se coloca en la cuadricula los diferentes valores que toma la salida para las diferentes combinaciones. Después se hacen grupos de “1” que estén juntos, se deben de coger todos los “1”. Los grupos pueden ser de 1, 2, 4, 8, 16 o 32. Karnaugh 3 variables

18. Simplificación Karnaugh 3 variables 1.-Tabla de verdad Forma canónica Miniterms Maxiterms

19. Simplificación Karnaugh 3 variables Tabla de karnaugh Se hacen los grupos y se colocan las variables de cada grupo que no cambian:

20. Representación de la función lógica con puertas lógicas La función lógica anterior se puede representar como:

21. Implementación con NAND o con NOR Cualquier función lógica se puede implementar utilizando exclusivamente puertas NAND o puertas NOR, para ello se emplean los Teoremas de Morgan.

22. Implementación con NOR Cuando queremos hacer el circuito con un determinado tipo de puertas y además nos dicen que debe de tener un numero determinado de entradas habrá que hacer las operaciones en función de las entradas.

23. Simplificación Karnaugh 4 variables Se hacen los grupos y se colocan las variables de cada grupo que no cambian igual que con 3 variables pero con la tabla ampliada.

24. Paso para la resolución de problemas Identificar las entradas y salidas. Elaborar la tabla de verdad. Simplificar la función. Implementar el circuito .

25. Ejemplo: Una máquina es accionada por 4 sensores a, b, c y d; de tal forma que la máquina se pondrá en marcha si: Cuando se activan dos. Cuando se activan cuatro de los detectores. Siempre que se active a y no este activado b, estén como estén los demás. Siempre que no esté activado ni a ni b, estén como estén los demás. ENTRADAS: a, b, c y d SALIDAS: accionamiento de la máquina S

26. Simplificación: Se puede realizar por cualquier método, la mejor manera es por karnaugh. Se hacen los grupos

27. Implementación con puertas lógicas Con todo tipo de puertas quedaría.

28. Condiciones especiales. En algunas condiciones especiales puede que la salida sea indiferente de cómo estén las entradas, en esos casos se pone un * y este puede actuar como 0 o como 1. Vamos a ver un ejemplo: Una alarma se activa cuando: 3 de sus 4 sensores están activados Con 2 es indiferente Con 1 o ninguno no se activa * 0 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 * 0 0 1 1 0 1 1 0 1 * 1 0 0 1 0 0 0 0 1 0 1 1 1 0 * 0 1 1 0 * 1 0 1 0 0 0 0 1 0 * 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 S D C B A

29. Simplificación mapa de Karnough con * Se cogen los “1” y si no interesa también podemos coger los *. Quedando la función como se detalla:

30. El circuito quedaría

31. Circuitos Combinacionales y Secuenciales. Dentro de la Electrónica Digital debemos distinguir: Combinacionales: En los que la salida depende única y exclusivamente del valor de las entradas Puertas lógicas. (los vistos hasta ahora) Decodificadores Codificadores Multiplexores Demultiplexores Circuitos aritméticos . Secuenciales: El valor de la salida depende del valor de las entradas y de cómo estuvieran anteriormente las salidas. Basculas Contadores Registros de desplazamiento

32. Codificadores Son circuitos que poseen n salidas y 2 n entradas. Al accionarse alguna de las entradas aparece un código previamente establecido en la salida. 1 1 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 0 0 s0 s1 e0 e1 e2 e3

33. Codificadores Pueden ser con prioridad o sin prioridad, como el anterior. Sin prioridad solo deben utilizarse cuando no pueden darse simultáneamente 2 entradas Con prioridad sería como se indica en la tabla siguiente. Ejemplo: Diseñar un codificador de decimal a BCD con prioridad 1 1 * * * 1 0 1 * * 1 0 1 0 * 1 0 0 0 0 1 0 0 0 s0 s1 e0 e1 e2 e3

34. Decodificadores Hacen la función inversa a los codificadores; a partir de un determinado código habilitan la salida correspondiente a ese código. Tienen: n: entradas 2 n salidas

35. Diseñar decodificador BCD a decimal con entrada de habilitación Tenemos 4 entradas y en función del numero binario de la entrada se activa la salida correspondiente. Además posee una entrada de habilitación de tal forma mientras esta entrada no este a “1” las salidas no serán activas. 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 1 1 1 0 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 * * * * 0 s0 s1 s2 s3 s4 s5 s6 s7 s8 s9 A B C D H

36. Decodificador BCD a 7 segmentos Es el decodificador encargado de activar los displays y así poder representar el numero binario . Se llaman 7 segmentos porque son las salidas que tiene correspondiente a las 7 entradas del display

37. Implementación de funciones con decodificadores Podemos representar una función con decodificadores. Dada la siguiente función. Construimos la tabla de verdad. Utilizando un decodificador de 3 entradas y tendrá 8 salidas si cogemos las salidas que son “1” y las unimos con una Or nos da la función que queremos representar 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 S c b a

38. Multiplexores Son circuitos que poseen 2 n entradas 1 salida y n entradas de control. Peden emplearse para convertir datos en paralelos en datos en serie. Diseñar un multiplexor con puertas.

39. Demultiplexores Hacen la función contraria a los multiplexores, son conversores serie paralelo. Poseen 1 entrada, 2 n salidas y n de control

40. Circuitos secuenciales Van a ser aquellos en que la salida no va depender exclusivamente del valor de las entradas, sino que también dependerá del valor que tenían las salidas en el estado anterior. Pueden considerarse como células elementales de memoria Se pueden distinguir diferentes tipos: RS JK T D Estas células pueden ser activadas por un reloj (ck) o no, además pueden tener entradas de preset y de clear.

41. Circuitos secuenciales El símbolo será: Cuando sean activadas por reloj este puede ser habilitado por - 1 (ck sin nada) - 0 (ck con negador (o)) - por flanco de subida (ck con>) - de bajada (ck con o>) .

42. Basculas RS con puertas NAND Q t-1 1 1 0 0 1 1 1 0 In 0 0 Qt S R

43. Basculas RS con puertas NOR In 1 1 0 0 1 1 1 0 Q t-1 0 0 Qt S R

44. Basculas RS con puertas NAND con ck Colocamos la entradas RS a través de una puerta NAND ya que “0” por lo que sea siempre es “0” y negado “1” y un “1” en las RS con NAND mantiene el estado anterior y por tanto no cambiara de estado mientras ck este a “1”. Observar que la Q se cambia de lugar .

45. Basculas RS con puertas NOR con ck Para conseguir el mismo efecto que en la anterior con puertas NOR necesitamos emplear puertas AND ya que en el caso de RS – NOR necesitamos un “0” para mantener el estado anterior y solo cambiará cuando tengamos un “1” en ck.

46. Biestable Jk Tabla de verdad Tabla de transiciones Cambia 1 1 1 0 1 0 1 0 Qt-1 0 0 Qt K J 0 * 1 1 1 * 0 1 * 1 1 0 * 0 0 0 K J Qt Qt-1

47. Diseño de un JK con RS NOR Queremos obtener Y disponemos de Cambia 1 1 1 0 1 0 1 0 Qt-1 0 0 Qt K J In 1 1 0 0 1 1 1 0 Q t-1 0 0 Qt S R

48. Diseño de un JK con RS NOR Hacemos la tabla de verdad Simplificamos por karnaugh y obtenemos 1 0 0 1 1 1 0 1 1 0 1 1 0 * 1 1 0 1 0 1 1 0 0 1 1 0 0 1 1 0 * 0 0 0 1 0 0 * 1 1 0 0 * 0 0 0 0 0 R S Qt Qt-1 K J

49. Resolución de circuitos secuenciales Para la resolución de circuitos ejercicios de secuenciales lo primero que hay que hacer es poner la tabla de transiciones de toda la secuencia. Se observa la secuencia y nos fijamos que no haya ninguna repetida. Harán falta tantos JK como salidas tenga la secuencia (Siempre que no haya ninguna repetida). Se rellena la tabla de los estados de los JK para que se cumplan sa secuencia, partiendo de la tabla de transiciones de los JK.

50. Ejemplo Diseño de un semáforo. Diseño de la tabla de transiciones del semáforo empezando por el semáforo apagado. * 1 0 * 1 * 0 0 0 1 * * 1 0 * 0 1 0 0 * 1 * * 1 0 0 1 0 * 0 * 1 * 0 0 0 Ambar J K Verde J K Rojo J K A V R 0 * 1 1 1 * 0 1 * 1 1 0 * 0 0 0 K J Qt Qt-1

51. Diseño de un semáforo. Una vez hecha la tabla de transiciones del semáforo se diseña se simplifica por karnaugh cada una de la entradas de los JK y se implementa la función con tantos Jk como salidas y con las puertas que realicen las funciones lógicas necesarias.

52. Mas Ejemplos con secuenciales Cartel luminoso. (Caen la letras) Contador en anillo. Luces coche fantástico. …

53. Circuitos secuenciales Contadores y registros de desplazamiento Contadores: Son circuitos secuenciales, con una entrada de impulsos, cuyo estado en cada instante muestra el número de impulsos recibidos. Pueden ser: Asíncronos o síncronos. Ascendentes o descendentes

54. Contador asíncorno El reloj se conecta sólo al primer JK y después la salida del primero se conecta a la entrada del siguiente y así sucesivamente.

55. Contador síncorno Son como los que hemos estado diseñado hasta ahora. El reloj va conectado a todo los JK Diseñar un contador que cuente de 0 a 9. Como lo hacíamos hasta ahora.

56. Registros de desplazamiento Se introducen datos en serie o en paralelo y se extraen en serie o en paralelo, todo ello sincronizado por un reloj