Ebook jaime casales

Universidad Nacional Autónoma
de
México
Jaime Casales Medina
Grupo 2401
Métodos Numéricos E-book

1
Índice
Método del Punto fijo ………………………………………………………………. 3
Método de Newton ………………………………………………………………….. 5
Método de Newton Modificado ………………………………………………… 8
Método de Broyden ……………………………………………………………….... 11
Método de Lagrange ………………………………………………………………… 16
Método de Diferencias Divididas ………………………………………………. 18
Método de Hermite ………………………………………………………………….. 20
Método de Spline Cúbico ………………………………………………………….. 22
Método de Diferencias Centradas ……………………………………………… 24
Método de Integración Numérica ………………………………………………. 26

2
Estos métodos:
 Solucionan ecuaciones no lineales tipo f(x)=0
 Normalmente cada método tiene sus requisitos
 Métodos son iterativos Métodos iterativos para resolver f(x)=0
En general métodos iterativos consisten en
1. Obtener una aproximación inicial x0
2. Refinar la aproximación inicial mediante una fórmula iterativa que genera
nuevos valores x1, x2, …,xn que, idealmente, convergerán a la solución
buscada x*.
3. Establecer un criterio de parada o test de finalización, satisfecho el cual, se
detiene el proceso de obtención de iterados. xk se llama iterado k – esimo y
el error de esta aproximación viene determinado por εk=│xk-x*│

3
Este método para determinar la solución de una ecuación que se expresa, para
alguna función g, de la forma g(x) = x. A una solución de esta ecuación se le llama
un punto fijo de la función g. Si para cualquier función g dada se puede encontrar
un punto fijo, entonces cada problema de búsqueda de las raíces de f(x) = 0 tiene
soluciones que corresponden precisamente a los puntos fijos de g(x) = x con g(x)
= x − f(x). La primera tarea entonces es decidir cuándo una función tendrá un
punto fijo y cómo se pueden determinar (es decir, aproximar con suficiente grado
de precisión) dichos puntos fijos. El siguiente Teorema da las condiciones
suficientes para la existencia y unicidad de un punto fijo.
Ejemplo:
𝑓1( 𝑥, 𝑦) = 𝑥2
− 𝑦 − 2 = 0
𝑓2( 𝑥, 𝑦) = 2𝑥𝑦 − 3 = 0
Paso 1: Sumar a f1 -4x y -5y a f2 para obtener las formas iterativas
𝑥 = 𝑔1( 𝑥, 𝑦) =
−𝑥2
+ 𝟒𝒙 + 𝑦 + 2
4
𝑦 = 𝑔2( 𝑥, 𝑦) =
−2𝑥𝑦 + 5𝑦 + 3
5
Paso 2: Derivar parcialmente las formas iterativas
𝜕𝑔1
𝜕𝑥
=
−2𝑥 + 4
4
,
𝜕𝑔1
𝜕𝑦
=
1
4
𝜕𝑔2
𝜕𝑥
=
−2𝑦
5
,
𝜕𝑔2
𝜕𝑦
=
−2𝑥 + 5
5

4
Paso 3: Graficar las funciones para poder dar valores iniciales aproximando la raíz
y así no tener que realizar tantas iteraciones
Paso 4: Sustituimos los valores (2,1) en las derivadas para saber si el sistema
converge
−2(2)+4
4
+
1
4
= 0 +
1
4
= |
1
4
| < 1 𝑝𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜 𝑐𝑜𝑛𝑣𝑒𝑟𝑔𝑒
−2(2)
5
+
−2(1)+5
5
=
−4
5
+
3
5
= |
−1
5
| < 1 𝑝𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜 𝑐𝑜𝑛𝑣𝑒𝑟𝑔𝑒
Paso 5: Realizamos las iteraciones sucesivas y simultaneas para encontrar la
solución del sistema
Sucesivas
i x y
0 2 1
1 1.75 0.9
2 1.7094 0.8846
3 1.7000 0.8831
4 1.6983 0.8832
5 1.6980 0.8833
6 1.6980 0.8834
7 1.6980 0.8834
Con la gráfica podemos
tomar como puntos iniciales
(x0, y0) al punto (2,1) que
son los que se aproximan a
la raíz.
Como tenemos 2 renglones
iguales nos detenemos ya que
el error es =0 por tanto ese
sería el resutultado

5
Simultaneas
El método de Newton es uno de los métodos numéricos más conocidos y
poderosos para la resolución del problema de búsqueda de raíces de f(x) = 0.
El método de Newton implica el generar la sucesión {Pn} definida por :
Pn = Pn−1 − f(pn−1) f 0 (pn−1) , n ≥ 1
Geométricamente, el método de Newton es equivalente a sustituir un arco
pequeño de la curva y = f(x) por una tangente trazada por un punto de la curva.
Supongamos, por definición, que f 00(x) > 0 para a ≤ x ≤ b y f(b) > 0. Tomemos,
por ejemplo, p0 = b para el cual f(p0) · f 00(p0) > 0. Trácese la tangente a la curva
y = f(x) en el punto B (p0, f(p0)). Como primera aproximación p1 de la raíz p
tomemos la abscisa del punto de intersección de esta tangente con el eje x.
Trácese nuevamente una tangente por el punto de coordenadas (p1, f(p1)), cuya
abscisa del punto de intersección con el eje x ofrece una segunda aproximación
p2 de la raíz p, y así sucesivamente.
i x y
0 2 1
1 1.75 0.8
2 1.68438 0.84000
3 1.68510 0.87405
4 1.69372 0.88491
5 1.69778 0.88539
6 1.69851 0.88411
7 1.69830 0.88344
8 1.69811 0.88330
9 1.69804 0.88333
10 1.69804 0.88336
Como tenemos 2 iteraciones con
variables iguales nos detenemos
ya que el error es =0 por lo tanto
ese es el resultado

6
Ejemplo:
𝑓1( 𝑥, 𝑦, 𝑧) = 𝑥2
− 𝑥 + 2𝑦2
+ 𝑦𝑧 − 10 = 0
𝑓2( 𝑥, 𝑦, 𝑧) = 5𝑥 − 6𝑦 + 𝑧 = 0
𝑓3( 𝑥, 𝑦, 𝑧) = 𝑧 − 𝑥2 − 𝑦2 = 0
Paso 1: Se calculan las derivadas parciales de cada función para poder crear la
matriz jacobiana
𝜕𝑓1
𝜕𝑥
= 2𝑥 − 1
𝜕𝑓1
𝜕𝑦
= 4𝑦 + 𝑧
𝜕𝑓1
𝜕𝑧
= 𝑦
𝜕𝑓2
𝜕𝑥
= 5
𝜕𝑓2
𝜕𝑦
= −6
𝜕𝑓2
𝜕𝑧
= 1
𝜕𝑓3
𝜕𝑥
= −2𝑥
𝜕𝑓3
𝜕𝑦
= −2𝑦
𝜕𝑓3
𝜕𝑧
= 1
Obteniendo:
J = [
2𝑥 − 1 4𝑦 + 𝑧 𝑦
5 −6 1
−2𝑥 −2𝑦 1
]
Paso 2: Graficamos las funciones para aproximar el vector (x0, y0, z0)
Con la gráfica podemos proponer
el vector x0 = (1,1,1)

7
Paso 3: Sustituimos los valores en la matriz jacobiana y en el vector Fx0 teniendo
como resultado
J = [
1 5 1
5 −6 1
−2 −2 1
] y Fx0
=[
(1)
2
− 1 + 2(1)2 + (1 ∗ 1) − 10
5(1) − 6(1) + 1
1 − (1)
2
− (1)
2
]
Paso 4: Utilizamos la extensión del método de newton para calcular el vector
siguiente con la formula Xn+1=Xn-1 - (J^ (-1)*Fxn-1) hasta que se cumpla la
tolerancia deseada
𝑥(1)
= [
1
1
1
] - [
1 5 1
5 −6 1
−2 −2 1
]
−1
∗ [
−7
0
−1
]
= [
1
1
1
] - [
1 5 1
5 −6 1
−2 −2 1
] ∗ [
−7
0
−1
]
= [
1
1
1
] - [
−7
0
−1
]
𝑥(1)
= [
1
1
1
]

8
Este método de Newton-Raphson modificado consiste en aplicar n (n número de
ecuaciones) veces el método de Newton univariable, una para cada variable. Cada
vez que se hace esto, se consideran las otras variables fijas.
Se eligen los valores iniciales (𝑥1 , 𝑥2, ⋯ , 𝑥𝑛) y empleando el método de Newton
se calcula un nuevo valor. Con lo cual se obtendría (𝑥11, 𝑥21, ⋯ , 𝑥𝑛1) y se
procede de forma sucesiva hasta alcanzar una tolerancia previamente establecida
Ejemplo:
𝑓1( 𝑥, 𝑦, 𝑧) = 𝑥2
+ 𝑦2
+ 𝑧2
= 9
𝑓2( 𝑥, 𝑦, 𝑧) = 𝑥𝑦𝑧 = 1
𝑓3( 𝑥, 𝑦, 𝑧) = 𝑥 + 𝑦 − 𝑧2
= 0
Emplear desplazamientos simultáneos y sucesivos, alcanzar una tolerancia de
0.0005.
Se realiza el mismo procedimiento que para Newton normal ya que solo existe una
leve modificación en el algoritmo
1 Se sacan las derivadas parciales
2 Se grafica para dar un vector inicial aproximado a la raíz
3 Después de realizar la primer iteración como Newton normal se utiliza la forma
f(n)/df(n) para las demás iteraciones que sean necesarias hasta cumplir la
tolerancia.

10
Para hallar la solución de la ecuación f(x)=0, el método de Newton emplea el jacobiano
en cada iteración. Sin embargo, computar ese jacobiano es una operación difícil y costosa. La
idea que subyace en el método de Broyden consiste en computar el jacobiano entero solamen
te en la primeraiteración, y llevar a cabo una actualización de rango 1 en las demás iteracione
s.
Ejemplo:
𝑓1( 𝑥, 𝑦) = 4𝑥2
− 3𝑦2
− 4𝑥 − 1
𝑓2( 𝑥, 𝑦) = 2𝑦 − cos( 𝑥 + 1) + 1
Paso 1: Se sacan las derivadas parciales para calcular la matriz jacobiana (para la primera
iteración que se realiza igual que en newton)
𝜕𝑓1
𝜕𝑥
= 8𝑥 − 4
𝜕𝑓1
𝜕𝑦
= −6𝑦
𝜕𝑓2
𝜕𝑥
= 𝑠𝑒𝑛( 𝑥 + 1)
𝜕𝑓2
𝜕𝑦
= 2
Entonces de igual forma graficamos para encontrar los puntos iniciales
Tomamos como punto inicial (0,0)
y (1,-1)

11
X0 Jacobiana Fx0 JInversa JInversa*F(x)
0 -4 0 -1 -.25 0 0.25
0 0.841470985 2 0.45969769 0.10518387 0.5 0.12466497
Paso 2: Obtenemos x1, Fx1, Ax1 y AF1. Después aplicamos Sherman Morrison
x1
-0.25
0.12466497
Obtenemos el primer resultado
F(x1)
0.203375933
0.018981183
Ax1 Fx1
-0.25 1.203375933
0.124664974 0.440716511
A1(-1)
-0.221105 -0.03646887
0.08763315 0.522151065

12
Se realiza el procedimiento anterior hasta llegar a la quinta iteración
NEWTON
x0 JACOBIANA F(x0) J(-1) J(-1)*F(x)
0 -4 0 -1 -0.25 0 0.25
0 0.841470985 2 0.45969769 0.10518387 0.5 0.12466497
SHERMAN M.
x1 F(x1) Ax1 AF1 Axt
-0.25 0.20337593 -0.25 1.20337593 -0.25 -0.12466497
-0.12466497 0.01898118 -0.12466497 -0.44071651
A1(-1)= MULTIPLICACIÓN DIVISIÓN
-0.221105 -0.03646887 0.00251104 -0.00316923 0.08690239
0.08763315 0.522151065 -0.0015252 0.00192498
-0.20434034 -0.08529463 0.04565966 -0.28867056 0.04565966 -0.02773352
-0.15239849 -0.00461069 -0.02773352 -0.02359188
-0.1614737 0.04039724 0.00023833 0.00030722 0.00399679
0.0566626 0.482229315 -0.00012378 -0.00015956
-0.21792692 -0.00169668 -0.01358658 0.08359795 -0.01358658 0.00705643
-0.14534207 -0.00013819 0.00705643 0.0044725
-0.16450567 0.037061058 -6.9612E-07 -7.6596E-07 0.00022959
0.0585015 0.484252724 4.222E-07 4.6456E-07
-0.21820092 2.2103E-05 -0.00027399 0.00171879 -0.00027399 0.00016618
-0.14517589 1.0947E-06 0.00016618 0.00013929
-0.16261087 0.039492625 1.9701E-10 2.5282E-10 1.0397E-07
0.05754069 0.483019737 -9.99E-11 -1.282E-10
-0.21819736 1.3223E-07 3.5509E-06 -2.197E-05 3.5509E-06 -1.8006E-06
-0.14517769 -4.611E-09 -1.8006E-06 -1.0993E-06
-0.16354762 0.038489216 -1.4767E-14 -1.5818E-14 1.5764E-11
0.05777317 0.483268754 3.6648E-15 3.9256E-15
-0.21819734 2.2437E-09 2.1803E-08 -1.2999E-07 2.1803E-08 -5.4109E-09
-0.14517769 -7.1205E-11 -5.4109E-09 4.5398E-09
-0.16643788 0.037165924 -1.4338E-18 -6.5646E-19 4.9608E-16
0.05851755 0.483609565 3.6928E-19 1.6907E-19

13
NEWTON
x0 JACOBIANA F(x0) J(-1) J(-1)*F(x)
1 4 6 -4 0.78609695 -2.35829085 -1.76749223
-1 0.90929743 2 -0.58385316 -0.35739797 1.5721939 0.51166149
SHERMAN M.
2.76749223 11.7107227 1.76749223 15.7107227 1.76749223 -0.51166149
-1.51166149 -1.21288652 -0.51166149 -0.62903336
0.10440295 -0.20228873 -18.9713766 60.0010098 27.8297545
-0.01320468 0.48360948 9.57881484 -30.2950374
1.2995049 -1.22400171 -1.46798733 -12.9347244 -1.46798733 0.74119971
-0.77046178 0.12498319 0.74119971 1.33786971
0.09604409 -0.16868869 -0.02495833 0.10032475 2.98585173
-0.00902144 0.46679419 0.01249051 -0.05020796
1.43814628 -0.59554744 0.13864138 0.62845427 0.13864138 -0.06938369
-0.83984547 0.0829265 -0.06938369 -0.04205668
0.18539635 -0.52615305 0.00099247 -0.0039705 0.01110739
-0.06435208 0.68815099 -0.00061458 0.0024587
1.59219064 0.14752164 0.15404435 0.74306908 0.15404435 -0.09539067
-0.93523614 -0.01763535 -0.09539067 -0.10056185
0.15404193 -0.39359416 -0.00127094 0.00537324 0.04053473
-0.0458375 0.60987583 0.00075048 -0.00317286
1.56252495 -0.01078601 -0.02966569 -0.15830765 -0.02966569 0.0175174
-0.91771874 0.00153572 0.0175174 0.01917107
0.14452482 -0.3539867 -1.2174E-05 5.0666E-05 0.0012792
-0.03982721 0.58486272 7.6884E-06 -3.1997E-05
1.56462742 -0.00021327 0.00210247 0.01057274 0.00210247 -0.00132776
-0.91904651 2.8909E-05 -0.00132776 -0.00150681
0.14694042 -0.36428455 1.4646E-08 -6.2439E-08 6.0633E-06
-0.04132176 0.5912341 -9.0619E-09 3.8632E-08

14
La interpolación y extrapolación numérica es quizás una de las herramientas más
utilizadas en aplicaciones numéricas a la Física. La situación frecuente es de una
función f de un conjunto de puntos x1,...,xn , donde falta una forma analítica. La
función f puede representar algunos puntos de datos del experimento o el
resultado de una computación a gran escala de una magnitud física que no se
puede convertir en una forma analítica sencilla. A continuación, puede ser
necesario evaluar la función f en algún punto x en el conjunto de datos x1,...,xn ,
pero donde x se diferencia de los valores tabulados. En este caso se trata de una
interpolación. Si x está fuera nos quedamos con el problema más preocupante, de
extrapolación numérica.

15
Corresponde al caso de interpolación lineal con polinomios algebraicos e identificación de los
valores de la función en los nodos de interpolación. Base de la interpolación: [ ] n B = 1, x, ... , x
Soporte (nodos) de la interpolación: [ ] n S x , x ,..., x = 0 1 Y el polinomio interpolador sería:
Los polinomios lk (x), k = 0,1,...,n se llaman Polinomios de Lagrange para la base B y el soporte
de interpolación S dado. 5 Así, pues, usando los polinomios de Lagrange, la fórmula de
interpolación en la base y soporte indicados tendría esta expresión para la función f(x):

16
Ejemplo:
La siguiente tabla relaciona los datos observados del voltaje y temperatura (°F)
para termopares formados por Platino y Platino -10% Rodio con juntas
refrigeradas a 32°
Estimar la temperatura para microvoltios de 300, 1700, 3300, 5300 y 5900
MVT T(ºF)
0 32
500 176
1000 296.4
1500 405.7
2000 509
2500 608.4
3000 704.7
3500 799
4000 891.9
4500 983
5000 1072.6
5500 1160.8
6000 1247.5
Sustituimos en la fórmula de lagrange los valores que queremos interpolar (300,
1700, 3300, 5300 y 5900)
Teniendo como resultado:
Polinomio Grado 2
300 121.232
1700 446.312
3300 761.448
5300 1125.7
5700 1195.66
Polinomio Grado 3
300 121.932
1700 447.6224
3300 761.4816
5300 1125.6944
5700 1195.6656

17
Los métodos para determinar la representación explícita de un polinomio de
interpolación, a partir de datos tabulados, se conocen como métodos de
diferencias divididas, y pueden usarse para derivar técnicas para aproximar las
derivadas y las integrales de funciones, así como para aproximar las soluciones de
ecuaciones diferenciales.
El tratamiento de las tablas de diferencias divididas supone que la función f(x) es
conocida para varios valores de x.
Ejemplo:
El problema a resolver es el mismo que el anterior visto (lagrange )
Paso 1: Hacemos la tabla donde calcularemos los valores de f[1], f[2], …, f[n]
donde f[n] debe satisfacer en los parámetros del grado de polinomio que se desea
y para esto utilizaremos la fórmula
𝑓[ 𝑥𝑖; 𝑥𝑖+1] =
𝑓[ 𝑥𝑖+1] − 𝑓[ 𝑥𝑖]
𝑥𝑖+1 − 𝑥𝑖
Teniendo como resultado:

18
Paso 2: Nos ubicamos en el renglón de la tabla que contenga el número más
cercano y que sea menor al punto que queremos interpolar y comenzamos a
trabajar con la formula
𝑃𝑛( 𝑥) = 𝑎0 + 𝑎1( 𝑥 − 𝑥0) + 𝑎2( 𝑥 − 𝑥0)( 𝑥 − 𝑥1) + ⋯
+ 𝑎 𝑛( 𝑥 − 𝑥0)( 𝑥 − 𝑥1) … (𝑥 − 𝑥 𝑛−1)
Adaptándola al grado del polinomio que se necesita

19
Dados una función real f definida en [a, b], r + 1 puntos distintos x0, . . . , xr en
dicho intervalo y enteros no negativos m0, . . . , mr, n de suerte que se satisfaga
(2.1) y que las derivadas de f que vamos a escribir existan, determinar un
polinomio Pn de grado menor o igual que n tal que Pn(x0) = f(x0), P0 n (x0) = f 0
(x0), . . . , P(m0) n (x0) = f (m0) (x0); Pn(x1) = f(x1), P0 n (x1) = f 0 (x1), . . . , P(m1)
n (x1) = f (m1) (x1); . . . . . . . . . . . . Pn(xr) = f(xr), P0 n (xr) = f 0 (xr), . . . , P(mr) n
(xr) = f (mr) (xr).
Ejemplo:
Un automóvil realiza un recorrido por una carretera recta y se cronometra su
recorrido en varios puntos, los cuales se muestran en la siguiente tabla.
t(seg) 3 5 8 13
d(pies) 225 385 625 993
v(pies/seg) 77 80 74 72
Estimar d(t=10s)
Paso 1: Calculamos los Lj(xj) y L’j(xj) apoyándonos en la siguiente fórmula:
𝐿0 =
(𝑥 − 𝑥1)(𝑥 − 𝑥2)
(𝑥0 − 𝑥1)(𝑥0 − 𝑥2)
L0=(X-5)(X-8)(X-13)/(3-5)(3-8)(3-13) L0'(x)=3x^2-52x+209/-100
L1=(X-3)(X-8)(X-13)/(5-3)(5-8)(5-13) L1'(x)=3x^2-48x+167/48
L2=(X-3)(X-5)(X-13)/(8-3)(8-5)(8-13) L2(x)=3x^2-42x+119/-75
L3=(X-3)(X-5)(X-8)/(13-3)(13-5)(13-8) L3(x)=3x^2-32x+79/400

20
Obteniendo:
i Xi f(xj) f'(xj) Lj(x) L'j(xj)
0 3 225 77 0.3 -0.8
1 5 385 80 -0.875 0.04166667
2 8 625 74 1.4 0.33333333
3 13 993 72 0.175 0.425
Paso 2: Continuamos con H= [1 − 2(𝑥 − 𝑥𝑗)𝐿′
(𝑥𝑗)]𝐿2
(𝑥) y con H’ =
(𝑥 − 𝑥𝑗)𝐿2.
Hn,j(x) Ĥn,j(x)
1.098 0.63
0.44661458 3.828125
-
0.65333333
3.92
0.10871875 -0.091875
Paso 3: Realizamos las sumatorias del método para calcular el punto interpolado
teniendo como resultado
∑f(xj)Hn,j(x) ∑f'(xj)Ĥn,j(x)
118.6210000 638.225
= 756.8460000

21
Este método ajusta un polinomio a un conjunto de datos usando una curva sin
oscilaciones. Parte de un conjunto de n+1 puntos y que no necesariamente están
igualmente espaciados. Los trazadores pueden ser de cualquier grado, aunque los
cúbicos son los más comunes por sus ventajas y características.
Este método consiste en buscar n curvas que conectan los puntos por pares: 0-1,
1-2, …, n-1 -n, las dos curvas que conectan los puntos k-1 y k y los puntos k y k+1,
deben de tener la misma pendiente en el punto k, lo cual produce una curvatura
continua.
Los coeficientes para este polinomio están dados por:
𝑎𝑖 =
𝑠𝑖+1 − 𝑠𝑖
6ℎ𝑖
𝑏𝑖 =
𝑠𝑖
2
𝑐𝑖 =
𝑦𝑖+1 − 𝑦𝑖
ℎ𝑖
− (
𝑠𝑖+1 + 2𝑠𝑖
6
)ℎ𝑖
Ejemplo:

22
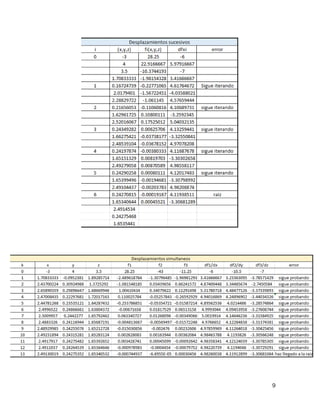
I xi yi hi F[1] si ai bi ci
0 0.62 2.14 0.12 6.83333333 0 -
1.28247133
0 8.11580466
1 0.74 2.96 0.26 -
0.61538462
-
64.1235665
3.45228836 -
32.0617833
4.26839067
2 1 2.8 0.78 1.02564103 15.5446265 -
2.98989176
7.77231323 -
2.04687154
3 1.78 3.6 0.64 -0.25 -
7.45454089
1.02719125 -
3.72727045
1.10826183
4 2.42 3.44 0.74 -
0.37837838
2.17537709 -
0.60219732
1.08768854 -
0.58107058
5 3.16 3.16 1.54 -
1.37662338
-
2.70730387
1.48588409 -
1.35365193
-
0.77788349
6 4.7 1.04 2.3 0.4173913 3.08185494 -2.6372627 1.54092747 -
0.48947917
7 7 2 2.08 -
0.70192308
-
3.79796081
4.56095709 -
1.89898041
-
1.31300093
8 9.08 0.54 1.28 1.09375 9.35864619 -
9.36589542
4.67932309 4.47011186
9 10.36 1.94 -0.84 -
1.97619048
-
34.5439886
-
4.83615841
-
17.2719943
-
11.6485073
10 9.52 3.6
g0(x)= -1.2825(x-0.62)^3+8.1158(x-0.62)+2.14
g1(x)= 3.4523(x-0.74)^3-32.0618(x-0.74)^2+4.2684(x-0.74)+2.96
g2(x)= -2.9899(x-1)^3+7.7723(x-1)^2-2.0469(x-1)+2.8
g3(x)= 1.0272(x-1.78)^3-3.7273(x-1.78)^2-2.0469(x-1.78)+3.6
g4(x)= -0.6022(x-2.42)^3+1.0877(x-2.42)^2-0.5811(x-2.42)+3.44
g5(x)= 1.4859(x-3.16)^3-1.3537(x-3.16)^2-0.7779(x-3.16)+3.16
g6(x)= -2.6373(x-4.7)^3+1.5409(x-4.7)^2-0.4895(x-4.7)+1.04
g7(x)=4.5610(x-7)^3-1.8990(x-7)^2-1.3130(x-7)+2
g8(x)= -9.3659(x-9.08)^3+4.6793(x-9.08)^2+4.4701(x-9.08)+0.54
g9(x)= -4.8362(x-10.36)^3-17.2720(x-10.36)^2-11.6485(x-10.36)+1.94

23
El método de e las diferencias finitas sirve para aproximar la solución de
ecuaciones diferenciales ordinarias y en derivadas parciales, las cuales van por lo
general acompañadas de condiciones iniciales o de frontera.
Mediante un proceso de discretización, el conjunto infinito de números que
representan la función o funciones incógnitas en el continuo, es reemplazado por
un número finito de parámetros incógnita, y este proceso requiere alguna forma de
aproximación.
Entre las formas de discretización esta: el método de los elementos finitos, método
de volúmenes finitos, método de diferencias finitas (1-D, 2-D, 3-D, 4-D), etc.
Ejemplo:
X Y
2.1 -4.67537977 3.43120058 0.98008807
2.3 -8.10658035 4.41128865
2.5 -12.517869
2.2 -6.2663599 1.84022045 -0.2469299
2.3 -8.10658035 2.08715035
2.4 -10.1937307
2.25 -7.15529017 0.95129018 0.06185194
2.3 -8.10658035 1.01314212
2.35 -9.11972247
f(x)= x^3Cosx
f´(x)= -x^3senx + 3x^2cosx
-19.6467958
h Dif. Prog. Error Dif.
Centrada
Error
0.2 19.60622308 0.0405727 19.60622308 0.0405727
0.1 -19.636854 0.00994177 -19.636854 0.00994177
0.05 -19.644323 0.00247277 -19.644323 0.00247277

24
Se nos plantea ahora el problema de calcular la derivada de una función de la que
sólo conocemos un número finito de datos. Dos métodos son los más usuales a la
hora de resolver tal problema: Derivar un polinomio de interpolación construido
mediante alguno de los métodos estudiados en el capítulo anterior. La función
permite el cálculo de las sucesivas derivadas en un punto dado del polinomio
interpolante asociado a nuestros datos.
Los métodos de integración numérica nos permiten integrar funciones que están
definidas analíticamente o de las que sólo conocemos su tabla en un número finito
de puntos. H.2. INTEGRACION NUM ´ ERICA ´ 75 Consideremos el caso en que
tenemos un conjunto de puntos a = x0 < x1 < . . . < xn = b igualmente espaciados
y que queremos calcular la integral de determinada función f definida sobre el
intervalo [a, b]. Podemos entonces considerar el polinomio interpolador de f
respecto a los nodos xi y su integral con la esperanza de así obtener una
aproximación a la integral de f.

26
Ejemplo:
El cuerpo de revolución que se muestra en la figura, se obtiene de girar la curva
dada por
y=1+〖(x/2)]^2 0≤x≤2
Entorno al eje x. Calcular el volumen
f(x)=〖π⌊1+ 〖(x/2)〗^2 ⌋〗^2 0≤x≤2
Paso 1: Acomodamos los datos
Paso 2: Identificamos que estén igualmente espaciados calculando H
h= 0.5
Paso 3: Sustituimos los valores en las fórmulas de trapecio, Simpson 1/3 y 3/8
Trapecio 11.98959384 Error de 0.02225167
Simpson 1/3 11.73188507 Error de 0.00027902
Simpson 3/8 11.75188363 error de 0.00198413
Valor exacto 11.72861257
Por lo tanto el método de integración por de 1/3 Simpson tiene menor error en este
ejercicio
x f(x)
0 3.141592654
0.5 3.546563582
1 4.908738521
1.5 7.669903939
2 12.56637061

Ebook jaime casales

Más contenido relacionado

La actualidad más candente

Similar a Ebook jaime casales

Último

Ebook jaime casales