Ecuaciones para el calculo de diferentes tipos de flujo

1. José Agüera Soriano 2011 1
ECUACIONES FUNDAMENTALES DE UN FLUJO

2. José Agüera Soriano 2011 2
ECUACIONES FUNDAMENTALES DE UN FLUJO
• ECUACIÓN DE CONTINUIDAD
• ECUACIÓN DE LA ENERGÍA
• ECUACIÓN CANTIDAD DE MOVIMIENTO
• APLICACIONES ECUACIÓN DE LA ENERGÍA
• RESALTO HIDRÁULICO

3. José Agüera Soriano 2011 3
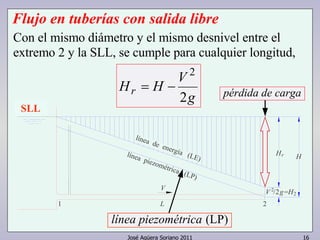
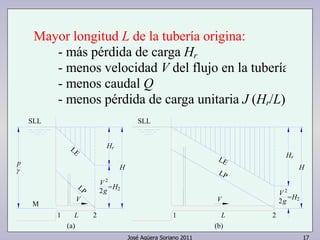
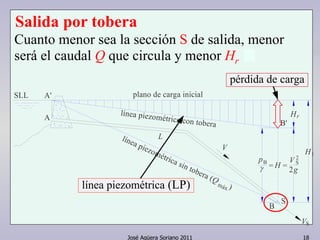
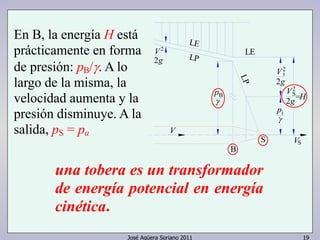
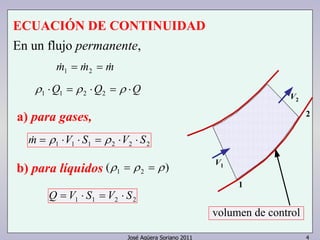
INTRODUCCIÓN
Son tres las ecuaciones fundamentales de un flujo:
• ecuación de continuidad (conservación de la masa)
• ecuación de la energía (conservación de la energía)
• ecuación de la cantidad de movimiento
(conservación de la cantidad de movimiento).

4. José Agüera Soriano 2011 4
ECUACIÓN DE CONTINUIDAD
En un flujo permanente,
volumen de control
V2
1
2
V1
mmm &&& == 21
QQQ ⋅=⋅=⋅ ρρρ 2211
222111 SVSVm ⋅⋅=⋅⋅= ρρ&
)( 21 ρρρ ==
2211 SVSVQ ⋅=⋅=
a) para gases,
b) para líquidos

5. José Agüera Soriano 2011 5
2
2
1
1
zg
p
zg
p
E ⋅+=⋅+=
ρρ
2
2
1
1
z
p
z
p
H +=+=
γγ
Energía de un líquido en reposo
o en metros de columna de líquido,
S.I.enJ/kg
2
2
zg
pV
E ⋅++=
ρ
m
2
2
z
p
g
V
H ++=
γ
Energía de un líquido en movimiento
o en metros de columna de líquido,

6. José Agüera Soriano 2011 6
SLL
plano de referencia
z1
γp /1
1V 2g/2
1H
2
2 /V 2g
γ/p2
z2
2H
12Hr
A
1
A'
B'
B
2
V
plano de carga inicial (PC)
línea piezométrica (LP) línea de energía (LE)
LP
Ecuación energía en conducciones de líquidos
H1 = H2 + Hr12 122
2
2
2
1
1
2
1
22
rHz
p
g
V
z
p
g
V
+++=++
γγ

7. José Agüera Soriano 2011 7
γp
gV 22
z
zp +γ = altura piezométrica
=altura cinética (desnivel entre LE y LP)
=altura de presión (desnivel entre LP y conducto)
= altura de posición respecto plano de referencia
SLL
plano de referencia
z1
γp /1
1V 2g/2
1H
2
2 /V 2g
γ/p2
z2
2H
12Hr
A
1
A'
B'
B
2
V
plano de carga inicial (PC)
línea piezométrica (LP) línea de energía (LE)
LP

8. José Agüera Soriano 2011 8
Ecuación energía en máquinas flujo líquido
Ht trabajo técnico, el que atraviesa los límites de la máquina
rt Hzz
pp
g
VV
H −−+
−
+
−
= 21
21
2
2
2
1
2 γ
H1 = H2 + |Hr12| + Ht
1H
z
turbina
plano de referencia
z1
1
Ht
2
2H H1
12
Ht
Hr
Ht
plano de referencia
bomba
1
1
2
Ht
H2
H 12r

9. José Agüera Soriano 2011 9
Ecuación energía en máquinas flujo líquido
H1 − H2 = |Hr12| + Ht
TURBINA
HH1 2
Hr
Ht
tH
He
mH
BOMBA
1H H2 Hr
He
Ht
tH Hm

10. José Agüera Soriano 2011 10
Turbina de reacción
Potencia de un flujo
(W)J/sHQgP ⋅⋅⋅= ρ
(J/kg)sm
sm:Gravedad
m:Altura
kg/s
mkg:Densidad
sm:Caudal
22
2
3
3
Hg
g
H
Q
Q
⋅



⋅



ρ
ρ

11. José Agüera Soriano 2011 11
EJERCICIO
La energía de un caudal de agua, de 60 m3
/s,
es, H= 50 m. Calcúlese su potencia.
Solución
CV)(40000kW29430W1029430
506081,91000
3
=⋅=
=⋅⋅⋅=⋅⋅= HQP γ

12. José Agüera Soriano 2011 12
ECUACIÓN DE LA CANTIDAD DE MOVIMIENTO
Cuando a lo largo de un volumen de control, la velocidad
del flujo varía, es porque actúan fuerzas sobre él que lo
aceleran:
amF
r
& ⋅=Σ
1V
C
VF
A
V1 Σ
D
C
2
A
FΣ
D
α
V2
B

13. José Agüera Soriano 2011 13
V1
A 'A
B'B
m 1
α
D '(c)
D
ΣF
V2
C'
2m
C
)( dtF ⋅Σ
)( Vmd ⋅
pdVmddtF
r
=⋅=⋅Σ )(
pd
r
)()( CDB'A'A'ABB'C'CDD'CDB'A'
ABCDD'C'B'A'
pppp
pppd
rrrr
rrr
+−+=
=−=
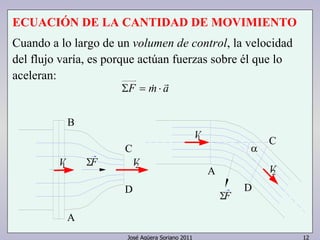
El impulso sobre la masa del volumen de control
provocará una variación de su cantidad de movimiento [ ]:
Esta variación del sistema es la corresponde al instante
(t + dt), menos la que tenía en t:
V1
A'A
B'B
m1
α
D'(c)
D
ΣF
V2
C'
2m
C

14. José Agüera Soriano 2011 14
V1
A'A
B'B
m1
α
D'(c)
D
ΣF
V2
C'
2m
C
11221122
A'ABB'C'CDD'
VdtmVdtmVmVm
pppddtF
⋅⋅−⋅⋅=⋅−⋅=
=−==⋅Σ
&&
rrr
1122 VmVmF ⋅−⋅=Σ &&
Por ser el régimen permanente
válida para líquidos y para gases
)( 12 VVmF −⋅=Σ &

15. José Agüera Soriano 2011 15
APLICACIONES ECUACIÓN DE LA ENERGÍA
Salida por un orificio
p
γ
V
2
V
=g2
H
SLL
ap
g
V
H
2
2
=
HgV ⋅⋅= 2

16. José Agüera Soriano 2011 16
línea piezométrica (LP)
línea de energía (LE)
L
V
1
SLL
g
2
V 2
2/ H= 2
H Hr
Flujo en tuberías con salida libre
SLL
pérdida de carga
línea piezométrica (LP)
Con el mismo diámetro y el mismo desnivel entre el
extremo 2 y la SLL, se cumple para cualquier longitud,
g
V
HHr
2
2
−=

17. José Agüera Soriano 2011 17
Mayor longitud L de la tubería origina:
- más pérdida de carga Hr
- menos velocidad V del flujo en la tubería
- menos caudal Q
- menos pérdida de carga unitaria J (Hr/L)
M
1
(a)
L 2
LP
LE
γ
p
V
SLL
r
H
V 2
2g
= 2H
H
SLL
1
(b)
L 2
LP
V
LE
g
V
2
2
H= 2
H
rH

18. José Agüera Soriano 2011 18
línea piezométrica sin tobera (
)
V
p
γ
Q
máx
B
SV
H
S
== HB SV
g2
2
1
línea piezométrica con tobera
plano de carga inicialSLL
A
A'
L
rH
B'
LEV 2
LP
V
2g
B
S
γ
Bp
LP
γ
i
VS
2g
=2g
p
SV 2
H
iV 2
LE
línea piezométrica sin tobera (
)
V
p
γ
Q
máx
B
SV
H
S
== HB SV
g2
2
1
línea piezométrica con tobera
plano de carga inicialSLL
A
A'
L
rH
B'
B
línea piezométrica (LP)
pérdida de carga
Salida por tobera
Cuanto menor sea la sección S de salida, menor
será el caudal Q que circula y menor Hr

19. José Agüera Soriano 2011 19
LEV2
LP
V
2g
B
S
γ
Bp
LP
γ
i
VS
2g
=2g
p
SV2
H
iV2
LE
una tobera es un transformador
de energía potencial en energía
cinética.
En B, la energía H está
prácticamente en forma
de presión: pB/γ. A lo
largo de la misma, la
velocidad aumenta y la
presión disminuye. A la
salida, pS = pa

20. José Agüera Soriano 2011 20
EJERCICIO
g
V
D
L
Hr
2
02,0
2
⋅⋅=
Solución
Velocidad en la conducción
r
r
r
H
H
g
V
g
V
D
L
H
⋅=
⋅
⋅
=
⋅⋅=
005,0
1000002,0
1
2
2
02,0
2
2
sm981,1;m2,022
== VgV
Calcúlese la sección de salida de la tobera al final de una
conducción, de 10 km y 1 m de diámetro, origine la pérdida
de 40 m en un salto de 400 m.
Tómese,

21. José Agüera Soriano 2011 21
Caudal
sm556,1981,15,0 322
=⋅⋅=⋅⋅= ππ VrQ
Velocidad de salida
sm04,84m;3602 S
2
S === VgVH
Diámetro de salida
m154,0;04,84556,1 SSS === DVQS

22. José Agüera Soriano 2011 22
Conducción hidroeléctrica de Villarino
m30m;0,8
m60m;,07
m40m;5,7
m402
m15000
==
==
==
=
=
r
r
r
HD
HD
HD
H
L

23. José Agüera Soriano 2011 23
Tubo de Pitot
γ
p
g
v
h +=
2
2
h
M

24. José Agüera Soriano 2011 24
FV
p
1
A
2
D
F
C
B
Fr
1·1p S
1
G
2
· S
p
2
2
F
rp FFF +=
=⋅ 11 Sp
=⋅ 22 Sp
=− F
=G
GFSpSpF +−+⋅+⋅=Σ )(2211
Fuerza sobre un conducto corto
Valoración indirecta de la fuerza F
fuerza sobre la sección 1
fuerza sobre la sección 2
fuerza que ejerce la pared
fuerza de gravedad
(Fr insignificante)
Las fuerzas sobre el volumen de control entre 1 y 2 son:
1·1p S
1
G
2
·S
p
2
2
F
FV
p
1
A
2
D
F
C
B
Fr

25. José Agüera Soriano 2011 25
GFSpSpF +−+⋅+⋅=Σ )(2211
)( 12 VVmF −⋅=Σ &
F
)( 122211 VVmGSpSpF −⋅−+⋅+⋅= &
)( 122211 VVmSpSpF −⋅−⋅+⋅= &
2211 SpSpF ⋅+⋅=
Por otra parte,
Igualando y despejando
En conductos cortos, G ≈ 0), en cuyo caso,
Cuando no hay flujo,

26. José Agüera Soriano 2011 26
Generalmente la fuerza será mayor cuando no hay flujo.
Las presiones a sustituir en las fórmulas anteriores son la
diferencia entre la interior y la que actúa exteriormente
sobre el conducto. Si ésta fuera mayor, los términos de
presión cambiarían de signo y con ello la fuerza F.
Cuando la presión exterior es la atmosférica, las presiones
a sustituir son las relativas.

27. José Agüera Soriano 2011 27
EJERCICIO
Calcúlese la fuerza sobre el codo de una conducción
hidráulica, de 90o y de 2,8 m de diámetro,
a) cuando fluyen 38,75 m3/s y la presión manométrica
es de 8 bar,
b) cuando el flujo se anula bruscamente, momento
en el que se prevé que la presión en el codo se eleve
a 13 bar.
Solución a)
Velocidad media
m/s29,6
4,1
75,38
2
=
⋅
==
πS
Q
V

28. José Agüera Soriano 2011 28
)( 122211 VVmSpSpF −⋅−⋅+⋅= &
kN5169,8N51697662437374926029
29,675,3810004,1108
0
25
111
==+=
=⋅⋅+⋅⋅⋅=
=⋅⋅++⋅=
π
ρ VQSpFx
kN5169,8
N51697662437374926029
2967538100041108
0
25
222
=
==+=
=⋅⋅+⋅⋅⋅=
=⋅⋅+⋅+=
,,,
VQSpFy
π
ρ
Fuerza sobre el codo
y
V1S·p1 1
p
x
22·S
2V
2
Fx
1
FFy

29. José Agüera Soriano 2011 29
y
V1S·p1 1
p
x
22·S
2V
2
Fx
1
FFy
Solución b)
2211 SpSpF ⋅+⋅=
kN8004,8N8004797
4,110130 25
11
==
=⋅⋅⋅=+⋅= πSpFx
kN8004,8N8004797
4,110130 25
22
==
=⋅⋅⋅=⋅+= πSpFy
El anclaje del codo hay que calcularlo para esta última
situación más desfavorable.

30. José Agüera Soriano 2011 30