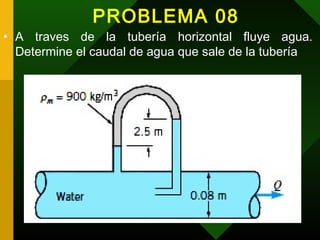
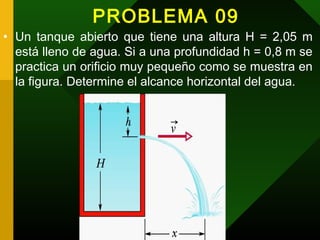
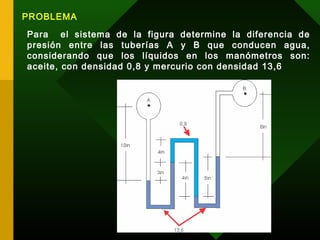
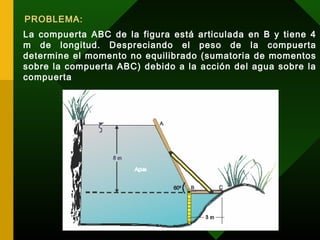
Este documento trata sobre hidrodinámica y contiene información sobre fluidos en movimiento, ecuaciones como la de continuidad, Bernoulli y Torricelli, y aplicaciones como medidores de caudal como el tubo Venturi y tubo de Pitot. Explica conceptos clave como línea de corriente, tubo de corriente, viscosidad y tipos de flujo. También incluye un ejemplo de cálculo sobre la presión, altura y potencia de un chorro de agua saliendo de una tubería.

1. HIDRODINAMICA
2013
FÍSICA II

2. Después de estudiar este tema,
deberá estar en condiciones de:
• Definir un fluido ideal y diferenciarlo de un fluido
real
• Aplicar la ecuación de continuidad en la
solución de problemas
• Formular y aplicar la ecuación de Bernoulli en la
solución de problemas.
• Aplicar el Teorema de Torricelli a situaciones
reales

3. HIDRODINÁMICA
Estudia los fluidos en movimiento, es decir,
el flujo de los fluidos

4. VISCOCIDAD
• Aparece como producto de la interacción de las moléculas
del fluido cuando éste se mueve a través de ductos en los
flujos laminares y turbulentos. Es decir la viscosidad se
debe al rozamiento interno del fluido
• La viscosidad en los líquidos disminuye con el aumento de
la temperatura mientras que en los gases sucede lo
contrario

5. Flujo de fluidos
• Se denomina flujo de fluidos al movimiento de fluidos.
Pueden ser:
• (a) Permanente y no permanente
• (b) Uniforme y no uniforme
• (c) laminar o turbulento
• (d) Real o Ideal
• (e) Rotacional e irrotacional
• (f) Viscoso y no viscoso
• (g) Compresible e incompresible

6. LINEA DE CORRIENTE
 Las líneas de corriente son líneas imaginarias dibujadas a
través de un fluido en movimiento y que indican la dirección de
éste en los diversos puntos del flujo de fluidos.
 Debe observarse que la tangente en un punto a la línea de
corriente nos da la dirección instantánea de la velocidad de las
partículas del fluido, en dicho punto.

7. TUBO DE CORRIENTE
Es la parte de un fluido limitado por un haz de líneas de corriente.
Todas las partículas que se hallan en una sección de un tubo de
corriente, al desplazarse continúan moviéndose por su sección sin
salirse del mismo. De igual forma ninguna partícula exterior al tubo
de corriente puede ingresar al interior del tubo.

8. ECUACIÓN DE
CONTINUIDAD
Es la expresión de la
ley de conservación
de la masa en el flujo
de fluidos.
Masa que pasa por la sección
1 es igual a la masa que pasa
por la sección 2
212121 VVVVmm =⇒=⇒= ρρ
t
x
A
t
x
A
xAxA
2
2
1
1
2211
=
=
2211 vAvA =
.cteAvQ ==

9. ECUACIÓN DE
CONTINUIDAD
De acuerdo a la conservación de la
masa, la cantidad de masa que fluye a
través de la tubería es la misma
1 2
1 1 1 2 2 2
1 1 2 2
m
Av
t
m m
Av t A v t
Av A v
Q Av
ρ
ρ ρ
=
∆
∆ = ∆
∆ = ∆
=
=
Si el flujo es incompresible,
la densidad es constante
Ecuación de
continuidad
A esta ecuación se llama caudal o gasto
En ausencia de fuentes y
sumideros en el sistema,
la masa de fluido por
unidad de tiempo que
fluye por las secciones 1
y 2 es la misma
cteAvQ ==

10. Ecuación de Bernoulli
 Constituye una expresión del principio de conservación de la
energía. Se considera que en el flujo existen tres tipos de energía: la energía
cinética debida al movimiento, la energía de presión debida a la presión y la
energía potencial gravitatoria debida a la elevación. Para una línea de corriente
de un fluido sin fricción tenemos:
2 2
1 1 2 2
1 2
2 2
p v p v
y y
g gγ γ
+ + = + +
2
2
p v
y H Cte
gγ
+ + = =

11. Cuando hay un conjunto de líneas de corriente en el flujo de
un fluido las velocidades de estas líneas es diferente en
cada una, por ello se introduce un coeficiente llamado
COEFICIENTE DE CORIOLIS la magnitud de este
coeficiente está entre 1 y 2, generalmente se usa 1.
α
ctez
P
g
v
B =++=⇒
γ
α
2
2
Para puntos 1 y 2 de un sistema en el cual hay bombas,
turbinas y se considera las pérdidas por fricción, el Bernoulli se
expresa como:
BOMBAS FRICCIÓ
N
TURBINA
S
Energía adicional
suministrada
Energía
perdida
Energía
extraída Energía en 2Energía en 1 =+
_ _
1 2
)
2
()
2
( 2
2
2
2
1
1
2
1
z
P
g
v
EEEz
P
g
v
eps ++=−−+++
γ
α
γ
α

12. )
2
()
2
( 2
2
2
2
1
1
2
1
z
P
g
v
EEEz
P
g
v
eps ++=−−+++
γ
α
γ
α
En la ecuación de Bernoulli en términos de carga es:
Carga de
velocidad
Carga
de
presión
Carga de
elevación
Pérdida
de carga
POTENCIA HIDRÁULICA (PH): llamada también potencia bruta
BQPH γ=
POTENCIA DE BOMBA (PB): es la
diferencia entre la potencia de salida y la
potencia de entrada dividida entre la eficiencia
de la bomba (eficiencia= trabajo
producido/energía recibida).
Eficiencia
BBQ
P ES
B
)( −
=
γ

13. APLICACIONES DE LA ECUACION DE BERNOULLI.
1. La presión hidrostática.
Para determinar la presión
hidrostática en el interior del fluido
se aplica la ecuación de Bernoulli
entre los puntos 1 y 2 del sistema
Como el depósito está abierto sobre
la superficie libre del fluido actúa la
presión atmosférica p0. Así mismo,
debido a que el fluido está en
reposo, v1 y v2 son nulas, con lo que
la ecuación anterior se escribe
2 2
1 1 2 2
1 2
2 2
p v p v
z z
g gγ γ
+ + = + +
( )
01
1 2
1 0 2 1
1 0
0 0
pp
z z
p p z z
p p h
γ γ
γ
γ
+ + = + +
= + −
= +

14. APLICACIONES DE LA ECUACION DE BERNOULLI.
2. Teorema de Torricelli.
 Permite determinar la velocidad de
salida de un fluido a través de una
boquilla. Se aplica la ecuación de
continuidad
 La ecuación de Bernoulli nos da
 Debido a que las presiones en los
puntos 1 y 2 son las mismas esto es
la presión atmosférica p0, la
2 2
1 1 2 2
1 2
2 2
p v p v
z z
g gγ γ
+ + = + +
1 1 2 2Av A v=
( )
2 2
0 01 2
1 2
2 2
2 1 2 1
2 2
2 1
2 2
2
2
p pv v
z z
g g
v v g z z
v v gh
γ γ
+ + = + +
− = −
− =

15. APLICACIONES DE LA ECUACION DE BERNOULLI.
2. Teorema de Torricelli..
 De las ecuaciones anteriores se
tiene
 En general el área de la tobera A2 es
mucho menor que el área de la
sección transversal del depósito A1,
de tal forma que
 Esta ecuación indica que la
velocidad de descarga es igual a
la velocidad que alcanzaría una
partícula cayendo libremente sin
fricción desde el punto 1 hasta el
punto 2. En otras palabras la
energía potencial de la superficie
libre se convierte en energía
cinética del chorro.
( )
2
2 2
2
1
2 2
1 2
1 2
2
1 /
A
v gh
A
gh
v
A A
  
 − = ÷
   
=
 −
 
2 2v gh=
TEOREMA DE

16. Tubo Venturi
• El medidor mostrado en la figura consiste en un tubo con un
estrechamiento en forma gradual y un aumento también gradual
practicado con la finalidad de evitar la formación de remolinos
quedando de esta forma asegurado un régimen estacionario
(permanente).

17. Tubo Venturi
• Para aplicar las ecuaciones de mecánica de
fluidos es necesario observar las líneas de
corriente

18. Tubo Venturi
 Para determinar el caudal en primer
lugar se determina la velocidad de flujo
del fluido aplicando la ecuación de
continuidad entre los punto 1 y 2
 Por otro lado aplicando la ecuación de
Bernoulli entre los puntos 1 y 2 se
tiene
• Observando la figura se ve que
z1 y z2 se encuentran en un
mismo nivel horizontal por lo
que
• Combinando las ecuaciones 1 y 2
2 2
1 1 2 2
1 2
2 2
p v p v
z z
g gγ γ
+ + = + +
2 2
1 1 2 2
2 2
p v p v
g gγ γ
+ = +
( )2 2
2 1 1 2
2g
v v p p
γ
− = −
( )1 2
2 2
2
1
2
1
g p p
v
A
A
γ
−
=
  
−  ÷
   
2211 vAvA =
2
1
2
1 v
A
A
v = (1)
(2)

19. Tubo Venturi
 La diferencia de presiones se
determina a partir de las
lecturas de los manómetros,
es decir
 Entonces la velocidad se expresa en
la forma
 Entonces el caudal Q o régimen
de flujo volumétrico se expresa en
la forma
1 0 1p p hγ= +
2 0 2p p hγ= +
1 2p p hγ− =
2 2
2
1
2
1
g h
v
A
A
γ
γ
=
  
−  ÷
   
( )
1 1 2 2
1 2 2 2
1 2
2
Q Av A v
gh
Q A A
A A
= =
=
−

20. Tubo de Pitot
• Este dispositivo se utiliza para medir
la velocidad del flujo de un gas,
consiste en un tubo manométrico
abierto que va conectado a una
tubería que lleva un fluido como se
muestra en la Figura
• La diferencia de presiones se
determina del manómetro
2 12 ( )g p p
v
γ
−
=
2 1 Hgp p hγ− =
2 Hgg h
v
γ
γ
=2 2
1 1 2 2
1 2
2 2
p v p v
z z
g gγ γ
+ + = + +
2
1 2 0
0 0
2 2
p pv
g gγ γ
+ + = + +

21. Tubo de Pitot

22. EJEMPLO:
De un depósito muy grande sale agua a través de una tubería
de 10 pulgadas de diámetro, la que por medio de una reducción
pasa a 5 pulgadas; descargando luego libremente a la
atmósfera. Si el caudal a la salida es 105 litros/segundo,
calcular:
a)La presión en la sección inicial de la tubería
b)La altura del agua en el depósito medida sobre el eje de la
tubería
c)La potencia hidráulica del chorro a la salida de la tubería
1
22
SOLUCIÓN
Debemos tener en cuenta que:
1 m3
= 106
cm3
=103
litros
1 pulgada=2,54 cm=0,0254 m
El caudal de salida es 0,105
m³/s
Q1=Q2=Q=Av=constante

23. sm
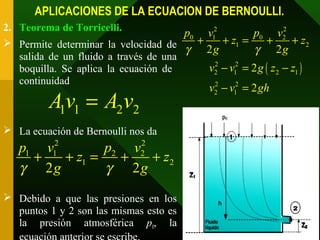
m
sm
A
Q
v /08,2
)]0254,0)(10[(
4
/105,0
2
3
1
1 ===⇒
π
sm
m
sm
A
Q
v /32,8
)]0254,0)(5[(
4
/105,0
2
3
2
2 ===⇒
π
a) Aplicamos el Teorema de Bernoulli para los puntos 1 y 2 en
el eje de la tubería
B1=B2
2
2
2
2
1
1
2
1
22
z
P
g
v
z
P
g
v
++=++
γγ 02
21
=
=
γ
P
zz Están en el
mismo
nivelPresión
manométrica
)(
222
2
1
2
21
2
21
2
1
vv
g
P
g
vP
g
v
−=⇒=+⇒
γ
γ
])/08,2()/32,8[(
)/81,9(2
/1000 22
2
3
1 smsm
sm
mkg
P −=
2
1 /33,0 cmkgP =

24. b) Para determinar h podemos utilizar el Teorema de Torricelli
debido a que al evaluar el Bernoulli en la superficie libre de
líquido en el recipiente y a la salida de la tubería de 5
pulgadas, la velocidad del fluido en el recipiente es
insignificante comparada con la velocidad de salida del fluido
en la tubería y ambos puntos están a presión atmosférica
)/81,9(2
)/32,8(
2
2 2
22
2
2
sm
sm
g
v
hghv ==⇒= mh 54,3=
c) La potencia hidráulica
es:
BQPH γ=
m
sm
sm
z
P
g
v
BB 53,3
)/81,9(2
)/32,8(
2 2
2
2
2
2
2
2 ==++==
γ
)
/75
1
)(/7,370()/105,0)(53,3)(/1000( 33
skgm
HP
skgmsmmmkgPH ==
HPPH 94,4=

25. EJEMPLO:
En el sistema que se representa en la figura la bomba BC
extrae 65 litros por segundo de un aceite de densidad 0,82 y lo
lleva desde el reservorio A hasta el D. La pérdida de carga
entre A y B es 8 m de aceite y entre C y D es 22 m de aceite.
Que potencia debe tener la bomba si su eficiencia es 80%?
SOLUCIÓN:
Eficiencia
BBQ
P ES
B
)( −
=
γ
smlmslQ /065,0)1000/1)(/65( 33
==
CDD
DD
S pz
P
g
v
B +++=
γ2
2
mmmBS 12222)10110(00 =+−++=
BS=122 m de
A la salida de la
bomba (punto C)

26. ABA
AA
E pz
P
g
v
B −++=
γ2
2
mmmBE 328)1050(00 =−−++=
80,0
)32122)(/065,0)(/1000)(82,0( 33
mmsmmkg
PB
−
=
)
/75
1
)(/25,5996(
skgm
HP
skgmPB =
HPPB 95,79=
BE=32 m de aceite
A la entrada de la
bomba (punto B)

27. PROBLEMA 01
En la figura, los diámetros interiores del conducto en las
secciones 1 y 2 son de 50 mm y 100 mm,
respectivamente. En la sección 1 fluye agua a 70°C con
velocidad promedio de 8 m/s. Determine: (a) la
velocidad en la sección 2, (b) el caudal

28. PROBLEMA 02
En la figura se muestra
un depósito muy grande
conteniendo un líquido
de densidad 0,8
sometido a una presión
de 300 k Pa. El depósito
descarga al ambiente
atmosférico a través de
una tubería de 10 cm de
diámetro
Determine la velocidad,
el caudal y la presión en
el eje de la tubería de
descarga

29. PROBEMA 03
• Un tanque abierto grande contiene una capa de aceite
flotando sobre el agua como se muestra en la figura.
El flujo es estable y carece de viscosidad. Determine:
(a) la velocidad del agua en la salida de la boquilla (b)
la altura h a la cual se elevará el agua que sale de
una boquilla de 0,1 m de diámetro.

30. PROBLEMA 04
• Fluye agua continuamente de un tanque abierto como se
muestra en la figura. La altura del punto 1 es de 10 m, y la de
los puntos 2 y 3 es de 2 m. El área transversal en el punto 2 es
de 0,03 m2
, en el punto 3 es de 0,015 m2
. El área del tanque es
muy grande en comparación con el área transversal del tubo.
Determine: (a) el flujo volumétrico y (b) la presión manométrica
del punto 2.

31. PROBLEMA 05
• Para el sifón mostrado en la figura, calcular: (a) el
caudal de aceite que sale del tanque, y (b) las
presiones en los puntos B y C.

32. PROBLEMA 06
• ¿Qué presión p1 se
requiere para obtener un
gasto de 0,09 pies3
/s del
depósito que se muestra
en la figura?. Considere
que el peso específico de
la gasolina es γ = 42,5
lb/pie3
.

33. PROBLEMA 07
• A través del sistema de tuberías fluye agua con
un caudal de 4 pies3/s. Despreciando la fricción.
Determine h.

34. PROBLEMA 08
• A traves de la tubería horizontal fluye agua.
Determine el caudal de agua que sale de la tubería

35. PROBLEMA 09
• Un tanque abierto que tiene una altura H = 2,05 m
está lleno de agua. Si a una profundidad h = 0,8 m se
practica un orificio muy pequeño como se muestra en
la figura. Determine el alcance horizontal del agua.

36. PROBLEMA 10
• A través de la tubería fluye aceite (SG = 0,83).
Determine el régimen de flujo volumétrico del aceite.

37. PROBLEMA 11
• Para el venturímetro mostrado en la figura.
Determine el caudal a través de dicho venturímetro

38. PROBLEMA 12
• El aceite de densidad relativa
0,80, fluye a través de una
tubería vertical que presenta
una contracción como se
muestra en la figura. Si el
manómetro de mercurio da
una altura h = 100 mm y
despreciando la fricción.
Determine el régimen de flujo
volumétrico

39. PROBLEMA
Para el sistema de la figura determine la diferencia de
presión entre las tuberías A y B que conducen agua,
considerando que los líquidos en los manómetros son:
aceite, con densidad 0,8 y mercurio con densidad 13,6

40. La compuerta ABC de la figura está articulada en B y tiene 4
m de longitud. Despreciando el peso de la compuerta
determine el momento no equilibrado (sumatoria de momentos
sobre la compuerta ABC) debido a la acción del agua sobre la
compuerta
PROBLEMA:

41. ¿Qué porción de un trozo de hierro se sumergirá
cuando está flotando en mercurio?
Datos: δ = 7.8 * 103
kg/m3
, (hierro)
δ = 13.6 *103
kg/m3
(mercurio)
PROBLEMA
V1
V2