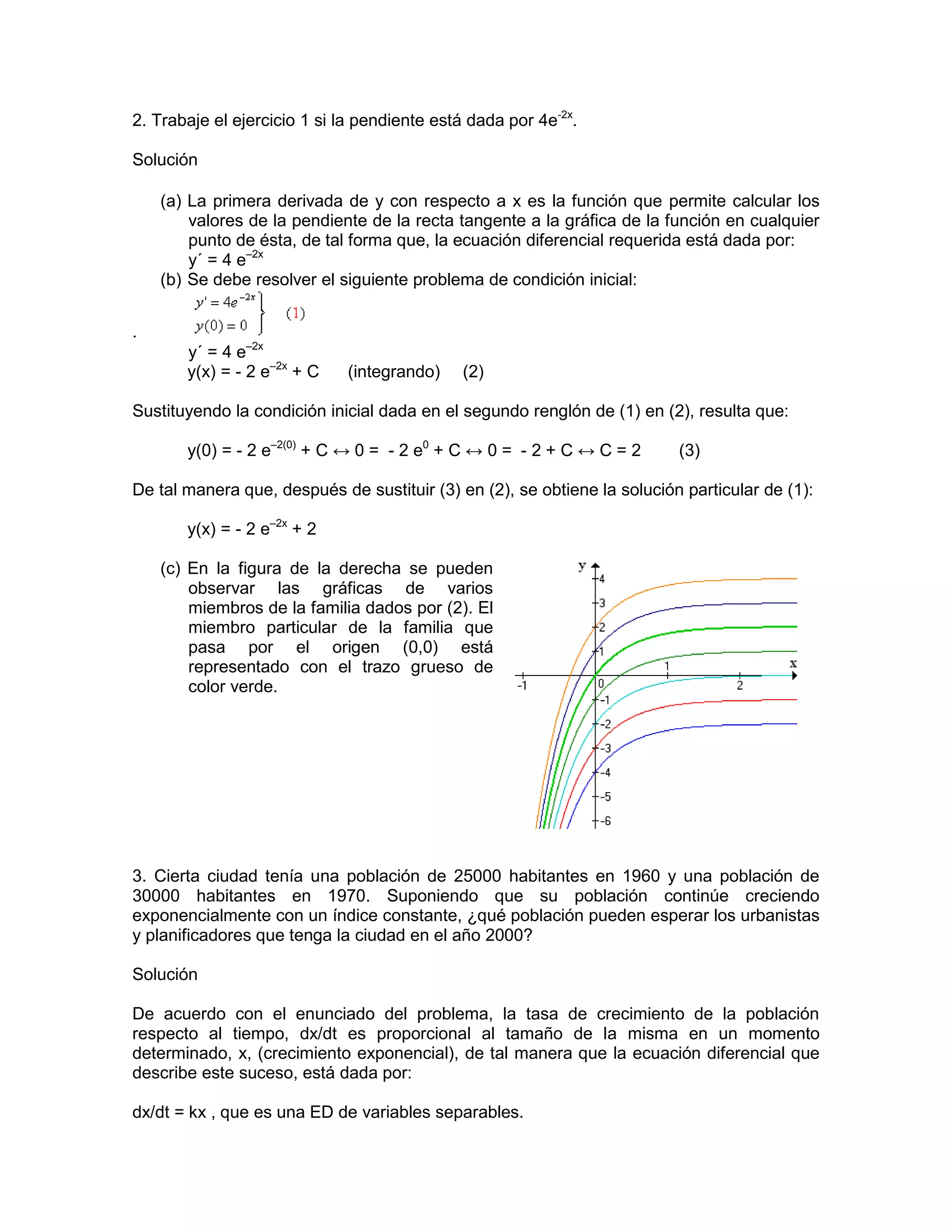
Este documento presenta 8 ejercicios de ecuaciones diferenciales de primer orden. El primer ejercicio establece una ecuación diferencial basada en la pendiente de una familia de curvas y encuentra la curva particular que pasa por el punto (0,0). El segundo ejercicio repite el primero pero con una pendiente diferente. El tercer ejercicio modela el crecimiento exponencial de la población de una ciudad. Los ejercicios restantes aplican modelos de crecimiento exponencial o decaimiento exponencial a diversos problemas biológicos y

1. Profr. Joel A. García Vargas Ecuaciones Diferenciales
Facultad de Ingeniería 2013-1 Grupo 02
EJERCICIOS ADICIONALES DEL CAPÍTULO 1, APLICACIONES
DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN
PARTE 1
1. La pendiente de una familia de curvas en cualquier punto (x,y) del plano xy está dada
por 4-2x. (a) Establezca la ecuación diferencial de la familia. (b) Determine una ecuación
para aquel miembro particular de la familia que pasa por el punto (0,0). (c) Dibuje varios
miembros de la familia incluyendo el hallado en (b).
Solución
(a) La primera derivada de y con respecto a x es la función que permite calcular los
valores de la pendiente de la recta tangente a la gráfica de la función en cualquier
punto de ésta, de tal forma que, la ecuación diferencial requerida está dada por:
y´ = 4 – 2x
(b) Se debe resolver el siguiente problema de condición inicial:
y´= 4 – 2x
y(x) = 4x – x2 + C (integrando) (2)
Sustituyendo la condición inicial dada en el segundo renglón de (1) en (2), resulta que:
y(0) = 4(0) – (0)2 + C ↔ C = 0 (3)
De tal manera que, después de sustituir (3) en (2), se obtiene la solución particular de (1):
y(x) = 4x – x2
(c) En la figura de la derecha se pueden
observar las gráficas de varios
miembros de la familia dados por (2).
El miembro particular de la familia que
pasa por el origen (0,0) está
representado con el trazo grueso de
color rojo.

2. 2. Trabaje el ejercicio 1 si la pendiente está dada por 4e-2x.
Solución
(a) La primera derivada de y con respecto a x es la función que permite calcular los
valores de la pendiente de la recta tangente a la gráfica de la función en cualquier
punto de ésta, de tal forma que, la ecuación diferencial requerida está dada por:
y´ = 4 e–2x
(b) Se debe resolver el siguiente problema de condición inicial:
.
y´ = 4 e–2x
y(x) = - 2 e–2x + C (integrando) (2)
Sustituyendo la condición inicial dada en el segundo renglón de (1) en (2), resulta que:
y(0) = - 2 e–2(0) + C ↔ 0 = - 2 e0 + C ↔ 0 = - 2 + C ↔ C = 2 (3)
De tal manera que, después de sustituir (3) en (2), se obtiene la solución particular de (1):
y(x) = - 2 e–2x + 2
(c) En la figura de la derecha se pueden
observar las gráficas de varios
miembros de la familia dados por (2). El
miembro particular de la familia que
pasa por el origen (0,0) está
representado con el trazo grueso de
color verde.
3. Cierta ciudad tenía una población de 25000 habitantes en 1960 y una población de
30000 habitantes en 1970. Suponiendo que su población continúe creciendo
exponencialmente con un índice constante, ¿qué población pueden esperar los urbanistas
y planificadores que tenga la ciudad en el año 2000?
Solución
De acuerdo con el enunciado del problema, la tasa de crecimiento de la población
respecto al tiempo, dx/dt es proporcional al tamaño de la misma en un momento
determinado, x, (crecimiento exponencial), de tal manera que la ecuación diferencial que
describe este suceso, está dada por:
dx/dt = kx , que es una ED de variables separables.

3. x-1 dx = k dt (separando variables)
(aplicando la integral)
Ln x = k t + C1 (integrando ambos miembros)
Despejando a x, se tiene que:
x(t) = exp (kt+C1) ↔ x(t) = exp(C1) exp (kt) ↔ x(t) = C ekt (1)
La función solución x(t) depende de dos parámetros: C y k, que deben determinarse con
los datos del problema.
Se toma t0 en 1960, de tal modo que: x(0) = 25000 (2)
Sustituyendo (2) en (1), resulta que:
25000 = C ek(0) ↔ C = 25000 (3)
Sustituyendo (3) en 81), resulta que:
x(t) = 25000 ekt (4)
Para determinar el valor de k, se emplea información del problema. En efecto, se sabe
que de 1960 a 1970, han transcurrido 10 años y que la población aumentó a 30000, por lo
que:
x(10) = 30000 (5)
Sustituyendo (5) en (4), se obtiene que:
30000 = 25000 ek(10) ↔ 6/5 = e10k ↔ 10k = Ln (1.2) ↔ k = 0.1 Ln (1.2) ↔
k ≈ 0.018232 (6)
Sustituyendo (6) en (4), se obtiene la expresión que permite calcular la el tamaño de la
población en función del tiempo t, en años:
x(t) = 25000 e0.018232 t
Del año 1960 al 2000, han transcurrido 40 años, por lo que el tamaño de la población está
dado por:
x(40) = 25000 e 0.018232(40) ↔ x(40) = 25000 e 0.72928 ↔ x(40) ≈ 51840
Por lo tano, para el año 2000 los urbanistas y planificadores deben esperar una población
aproximada de 51840 personas.

4. 4. En cierto cultivo de bacterias, su número se ha sextuplicado en 10h. ¿Qué tiempo tardo
la población en duplicar su número incial?
Solución
Suponiendo que la tasa de cambio ó rapidez de variación del número de bacterias con
respecto al tiempo, dx/dt, sea proporcional al número de bacterias en un momento
determinado, x, se tiene que:
dx
= k x , que es una ED de variables separables. Luego, se tiene que:
dt
⇒ x-1 dx = kdt (separando variables)
dx
⇒ ∫ x ∫
= k dt (aplicando la integral)
⇒ Ln x = k t + C1 (integrando ambos miembros)
tomando antilogaritmos se tiene que:
x(t) = e kt + C1 = e C1 e kt = C e kt (1)
Sean: C0 el número de bacterias en t=0 cuando se inicia el estudio
Ct población final (número de bacterias en el último conteo)
Por lo que (1) se puede escribir como:
Ct = C0 ekt (2)
Se sabe de las condiciones del problema, que el número de bacterias se ha sextuplicado
en 10 horas, por lo que se tiene que:
Ct = 6C0 ; t=10 (3)
Sustituyendo (3) en (2), resulta que:
Ln6
6C0 = C0 e10k ↔ 6= e10k ↔ Ln 6 = 10k ↔ k = = 0.1791759469 (4)
10
Por lo tano, sustituyendo (4) en (2), se tiene que:
Ct = C0 e0.1791759479t (5)
Se pide averiguar cuándo el n+umero de bacterias se duplicó, esto es, cuando Ct = 2C0,
t=?. Por tanto (5) se puede escribir como:
2 = C0 e0.1791759479t ↔ Ln 2 = 0.1791759469t ↔

5. Ln2
t= ≈ 3.8685h ; t = 3.8685h equivale a t = 3h 52´
0.1791759469
Por lo tanto la respuesta es: la población de bacterias se duplicó al cabo de
aproximadamente 3 horas y 52 minutos.
5. El carbono extraído de un cráneo antiguo contenía solamente una sexta parte del
carbono C14 extraído de un hueso de los tiempos actuales. ¿Cuál es la antigüedad del
cráneo?
Solución
La tasa de desintegración respecto al tiempo, dN/dt, de un material radioactivo de masa
N, es proporcional a N. Por tanto, la ecuación diferencial que describe cuantitativamente
esste fenómeno está dada por:
dN
= -k N (1)
dt
Para el carbono 14 el valor aproximado de k es de 0.0001216. De esta forma (1) se puede
escribir como:
dN
= - 0.0001216 N ; que es una ED de variables separables.
dt
dN
= - 0.0001216 dt (separando variables)
N
dN
∫ N = - 0.0001216 ∫ dt (aplicando la integral)
LnN = - 0.0001216 t + C1 (integrando)
Aplicando antilogaritmos, se tiene que:
N = e- 0.0001216 t + C1 = eC1 e −0.0001216t = C e0.0001216t (1)
Sea N0 la cantidad de C14 presente en el cráneo antiguo
N la cantidad de C14 presente en un hueso actual
Según los datos del problema, N0 = N/16, es decir N = 6 N0
Por lo que la función dada por (1), se puede escribir como:
Ln6
6N 0 = N 0 e-.0.0001216t ↔ 6 = e.- 0.0001216t ↔ t = = - 14734.86405 años
- 0.0001216

6. La respuesta es: El cráneo estudiado tiene una antigüedad aproximada de 14735 años.
6. El carbono extraído de una reliquia característica de los tiempos de Cristo contenía
4.6x1010 átomos de C14 por gramo. El carbono extraído de un especímen actual de la
misma sustancia contiene 5.0x1010 átomos de C14 por gramo. Calcule la edad aproximada
de la reliquia. ¿Cuál es su opinión sobre la autenticidad de la reliquia?
Solución
En este caso se tiene que:
N = 5.0 x1010 y N0 = 4.6 x1010 (1)
A partir del problema anterior (problema 13) puede deducirse que la función que permite
calcular la masa actual, N, de carbono C14 cocnociendo la cantidad de masa original, N0,
es función del tiempo t en años, está dada por la expresión:
N = N 0 e- 0.0001216t (2)
Sustituyendo (1) en (2), se obtiene:
5.0
5.0 x1010 = 4.6x1010 e- 0.0001216t ↔ e- 0.0001216t =
↔ e- 0.0001216t = 1.086956522
4.6
0.08338160918
− 0.0001216 t = Ln(1.086956522) ↔ t = − = −685.7años
0.0001216
Respuesta: La supuesta reliquia tiene una edad aproximada de 686 años (siglo
XIV). Parece que pretender meter gato por liebre, pues de acuerdo con los
resultados obtenidos, el material con que hecha la reliquia está lejos de ser de la
época de Cristo.
7. Cuando nació su primer hijo, una pareja depositó en una cuenta de ahorros
$5000 euros bajo interés compuesto continuo al 8%. Se dejó que se acumularan
los intereses devengados. ¿A cuánto ascenderá la cuesta en el decimoctavo
cumpleaños del niño?
Solución
El monto del dinero en una cuenta bajo interés compuesto crece
proporcioanalmente a la cantidad de dinero presente en la cuenta en un momento
determinado. De tal manera que la ecuación diferencial asociada a este hecho
está dada por:
dN
=kA (1)
dt

7. En estos casos la constante de proporcionalidad k es el rédito o interés porcentual:
1
8% ↔ 8 x = 0.08 Por lo que k = 0.08 (2)
100
Sustituyendo (2) en (1), se obtiene:
dN
= 0.08 A que es una ED de variables separables (es igual al modelo
dt
del decaimiento radioactivo y crecimiento de ciertas poblaciones como el caso de
bacterias). Su solución es de tipo exponencial. En efecto,
dN
= 0.08 dt (separando variables)
A
dN
∫ A
= 0.08 ∫ dt (aplicando la integral)
Ln A = 0.08 t +C1 (integrando)
Tomando antilogaritmos, se tiene que:
A = e0.08 t + C1 = eC1 e0.08tt = C e0.08t (3)
En el momento de abrir la cuenta los datos son t=0, A=5000 (4)
Sustituyendo (4) en (3), resulta que:
5000 = C e0.08t ↔ 5000 = C e0 ↔ C = 5000 (5)
Sustituyendo ahora (5) en (3), resulta que:
A = 5000 e0.08t (6)
Para conocer el monto del dinero A(t) en el momento en que el hijo cumple 18
años de edad, basta sustituir el valor de t=18 en (6). Es decir:
A = 5000 e0.08(18) = 5000 e1.44 = 5000 (4.220695817) = 21103 euros
Respuesta: Cuando el joven cumpla 18 años de edad, la cuenta ascenderá a $21103
euros aproximadamente.
8. Suponga que se usa un pentobarbitol sódico para anestesiar a un perro. El perro queda
anestesiado cuando la concentración en su corriente sanguínea es por lo menos de 45
miligramos (mg) de dicha sustancia por kilogramo de peso del perro. Suponga también
que el pentobarbitol sódico sódico es eliminado de la corriente sanguínea del perro en

8. forma exponencial, con una vida media de 5h. ¿Qué dosis simple debe administrarse para
tener anestesiado durante una hora a un perro de 50kg?
Solución
Como el medicamento es eliminado de la corriente sanguínea del perro en forma
exponencial, la ecuación diferencial que describe la tasa instantánea de disminución del
medicamento, dM/dt, para una cantidad presente de medicamento, M, al tiempo t en
horas, está dada por:
dM
= −k M El signo negativo implica disminución, y por tanto la
dt
constante k debe tomar un valor positivo. Este modelo matemático es una ED de variables
separables y es del mismo tipo que en varios de los ejemplos anteriores (ya se sabe como
resolverlo y además de qué forma es la solución)
dM
= - k dt (separando variables)
M
dM
∫ M
= - k ∫ dt (aplicando la integral)
LnM = - k t + C1 (integrando)
Aplicando antilogaritmos, se tiene que:
M = e − kt + C1 = eC1 e − kt = C e- kt (1)
Sea M0 la cantidad inicial del medicamento aplicada al tiempo t=0 (2)
Sustituyendo (2) en (1), se obtiene que:
M 0 = C e- k(0) = C ↔ C = M 0 (3)
Sustituyendo (3) en (1), resulta que:
M = M 0 e-kt (4)
Como el medicamento tiene una vida media de 5 horas, la mitad del medicamento se
eliminará de la corriente sanguínea del perro en ese tiempo. Si M0 es la cantidad inicial de
medicamento aplicada, M0/2 es la cantidad al cabo de 5 horas. Sustituyendo estos valores
en (1), se obtiene:
M0 1 1
= M 0 e -5k ↔ = e -5k ↔ Ln = -5k ↔
2 2 2

9. Ln(0.5)
k=− = 0.1386294361 (5)
2
Sustituyendo (5) en (4), se tiene que:
M = M 0 e-0.1386294t ↔ M 0 = M e0.1386294t (despejando M0) (6)
El perro pesa 50 kg y por cada kg de peso del perro se deben aplicar 45mg de
medicamento; y 50x45=2250mg. Sustituyendo este último valor en (6) se tiene que:
M 0 = 2250 e0.1386294t (la cantidad final de medicamento debe ser 2250mg) (7)
Se pide determinar qué cantidad mínima de medicamento debe aplicarse para que el
perro permanezca anestesiado por un lapso de 1 hora. De tal manera que:
M 0 = 2250 e0.1386294(1) = 2250 (1.148698355) = 2584.571mg
Respuesta: Para que el perro quede anestesiado por una hora, es decir, para que la
cantidad de droga esté por encima de 2250mg en el lapso de 1 hora, se debe aplicar una
dosis de aproximadamente 2585mg de pentobarbitol sódico.
9. Un tarro de crema, inicialmente a 25°C, se va a enfriar colocándola en el pórtico donde
la temperatura es de 0°C. Supóngase que la temperatura de la crema ha descendido a
15°C después de 20 min. ¿Cuándo estará a 5°C?
Solución
Sea T la temperatura de la crema, en función del tiempo t (medida en minutos, en °C
dT/dt es la rapidez con la que desciende la temperatura
T0 = 25, temperatura inicial de la crema en °C
Por tanto, se tiene que:
dT
= −k T que es una ED de variables separables (1)
dt
dT
= - k dt (separando variables)
T
dT
∫ T = - k ∫ dt (aplicando la integral)
LnT = - k t + C1 (integrando)

10. Aplicando antilogaritmos, se tiene que:
T = e − kt + C1 = eC1 e − kt = C e- kt (2)
Considerando la condición inicial en t=0, T(0)=25, se tiene que:
25 = C e- k(0) ↔ C = 25 (3)
Sustituyendo (3) en (2), resulta que:
T(t) = 25 e- kt (4)
Después de 20 minutos la temperatura ha descendido a 15°C; es decir, en t=20,
T(20)=15. Sustituyendo estos valores en (4), se obtiene que:
3 − 0.5105256
15 = 25 e- 20k ↔ = e- 20k ↔ Ln(0.6) = −20k ↔ k = −
5 20
k = 0.02554128 (5)
Despejando t de (4), se tiene que:
T T 1 T
T(t) = 25 e- kt ↔ = e- kt ↔ Ln( ) = −k t ↔ t = − Ln( ) (6)
25 25 k 25
Sustituyendo (5) y T=5 en (6), se obtiene que:
1 5 - 1.6094379
t=− Ln( ) = − = 63
0.02554128 25 0.02554128
Respuesta: La crema estará a una temperatura de 5°C aproximadamente en 63 minutos
después de haber sido puesta en el pórtico.
10. Una pelota se deja caer desde lo alto de un edificio de 400 pies de altura. ¿Cuánto
tardará en llegar al suelo? ¿Con qué velocidad golpeará el piso?
Solución
La aceleración de un cuerpo en caída libre es constante e igual al valor de g en las
unidades correspondientes. Por tanto,
dv
a(t) = = - g = -32 (la fuerza de la gravedad en el sistema inglés es 32pies/s2
dt
y esta ecuación diferencial es de variables separables)
dv = -32 dt (separando variables)

11. v(t) = - 32 ∫ dt = - 32 t + C1 (integrando)
Condición inicial: t=0; v(0)=0 (al soltar la pelota, la velocidad es nula)
v(0) = 0 = - 32 (0) + C1 ↔ C1 = 0 Por lo tanto:
v(t) = -32t (1)
dx
v(t) = = - 32t que es otra ED de variables separables.
dt
dv = -32 t dt (separando variables)
x(t) = - 32 ∫ tdt = - 16 t 2 + C2 (integrando)
Condición inicial en desplazamientos: t=0, x(0)=400 (la pelota se suelta de una
altura de 400 pies). Por tanto:
x(0) = 400 = - 16 (0)2 + C2 ↔ C2 = 400
Por lo que la función solución en desplazamientos esta dada por:
x(t) = - 16 t 2 + 400 (2)
Cuando la pelota llegue al suelo, x=0, es por ello que:
400
0 = - 16 t 2 + 400 ↔ t 2 = = 25 ↔ t = 5 es el valor aceptable de los dos
16
posibles (5 y -5). Sustituyendo el valor de t=5 en (1), se tiene que:
v(5) = -32 (5) = - 160 pies/s (el valor negativo implica que va en sentido opuesto al
del sistema de referencia puesto en el suelo. La aceleración, velocidad y desplazamiento
son vectores y es necesario identificar la dirección y sentido en la que actúan).
Respuesta. La pelota tarda 5 segundos en llegar al suelo y lo hace con una velocidad de
160pies/s.
11. Se aplican los frenos de un carro cuando el vehículo se mueve a 100km/h y
proporcionan una desaceleración constante de 10 metros por segundo en cada segundo
(m/s2). ¿Cuánto avanzará el carro antes de detenerse?
Solución
Primero es conveniente expresar la velocidad del carro en m/s para no cometer errores
con las unidades. En efecto,

12. km 100000 m 250 m
100 = =
h 3600 s 9 s
dv
a(t) = = −10 es una ED de variables separables
dt
dv=-10dt (separando variables)
v(t) = - 10 ∫ dt = −10t + C1 (integrando)
Condición inicial: t=0; v(0)= 250/9 (en el momento de aplicar los frenos la velocidad es
de 250/9 m/s). Por tanto, para determinar el valor de C1, se emplea la condición inicial.
250 250
v(0) = = − 10 (0) + C1 ↔ C1 = ; por lo tanto, resulta que:
9 9
250
v(t) = −10t + (1)
9
Pero, la velocidad expresada en términos de la distancia se escribe como:
dx 250
v(t) = = −10t + que es una ED de variables separables
dt 9
250
dx = (−10t + ) dt (separando variables)
9
250 250
∫ dx = ∫ (−10t + 9
) dt ↔ x(t) = −5t 2 +
9
t + C2
Condición inicial para desplazamiento o distancia: t=0, x(0)=0, Luego:
250
x(0) = 0 = −5(0)2 + (0) + C2 ↔ C2 = 0
9
Por tanto, resulta que:
250
x(t) = −5t 2 + t (2)
9
Cuando el auto se detiene, la velocidad es nula. Sustituyendo el valor v=0 en (1), se tiene
que:

13. 250 25
0 = − 10t + ↔t= (3)
9 9
Sustituyendo (3) en (2), resulta que:
25 25 250 25 3125 6250 3125
x( ) = −5( ) 2 + =− + = = 38.58
9 9 9 9 81 81 81
Respuesta: El vehículo recorrerá antes de detenerse una distancia de 38.58m.
12. Una pelota se arroja hacia arriba desde el nivel del suelo. Su velocidad inicial es de
160 pies/s. ¿Cuál es la altura máxima que alcanza la pelota? ¿Cuánto tiempo permanece
en el aire?
Solución.
Sea y0 = 0
v0 = 160
a = dv/dt = -32 es una ED de variables separables
dv = −32 dt ↔ ∫ dv = ∫ (−32) dt ↔ v = −32 t + C1 (1)
Pero v0 = 160=-32(0) + C1 → C1 = 160, de tal manera que (1) se puede escribir como:
v(t) = - 32 t +160 (2)
Además se tiene que:
dy
v= → dy = (−32 t + 160)dt ↔ ∫ dy = ∫ (−32t + 160) dt ↔ y = −16 t 2 + 160t + C2
dt
y(t) = -16t2+160t +C2 (3)
Pero y0 = 0 → C2 = 0, por lo que (3) se puede escribir como:
y(t) = -16t2+160t (4)
En el momento en que la pelota alcanza su altura máxima, la velocidad es nula. De (2) se
tiene que:
0 = -32t+160 → t = 5 segundos (5)
Para determinar la altura máxima, se sustituye (5) en (4), y resulta que:
y(5) = - 16 (5)2 +160 (5) = -400 + 800 = 400 pies (6)
Ahora, cuando la pelota llegue al suelo, y=0. De (4) se tiene que:

14. 0 = -16t2+160t
Que es un polinomio de grado dos y que puede escribirse como:
16t (t-10) = 0 ó t (t-10) = 0
Es decir, una raíz es nula y la otra raíz vale 10. Por lo tanto t = 10 segundos.
Respuesta: La pelota alcanza una altura máxima de 400 pies y permanece en el aire 10 s.