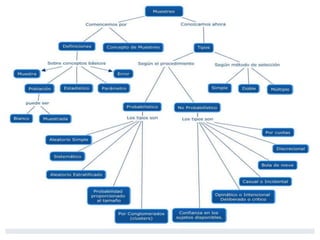
El documento define conceptos estadísticos fundamentales como población, muestra, variable, dato y parámetro. Explica que una población es un conjunto de personas u objetos con características comunes, mientras que una muestra es una subsección de la población seleccionada para su estudio. También diferencia entre variables cualitativas y cuantitativas.

1. Estadística
Alumno:
Edixon Figueroa

2. Población:
Una población se precisa como un conjunto
finito o infinito de personas u objetos que
presentan características comunes. Ejemplo:
Miembros del II semestre de Electricidad en el
Instituto Sucre.
Muestra:
"Una muestra debe ser definida en base de la
población determinada, y las conclusiones que
se obtengan de dicha muestra solo podrán
referirse a la población en referencia",
Cadenas (1974). Ejemplo: El estudio realizado
a 25 miembros del Instituto Sucre.
Muestra Aleatoria
Una selección que se escoge aleatoriamente por
azar o de forma imprevista. Ejemplo: una encuesta
Variable:
Es aquello que varía o puede variar. Se trata de
algo inestable, inconstante y mudable. En otras
palabras, una variable es un símbolo que
representa un elemento no especificado de un
conjunto dado. Ejemplo: Genero.

3. Dato:
Antecedentes necesarios para llegar al
conocimiento exacto de una cosa o para
deducir las consecuencias legítimas de un
hecho. Ejemplo: Nombre y Apellido.
Parametro:
Un valor que ya está "incluido" en una
función. Ejemplo: Si una función que calcula
la altura de un árbol es h(años) = 20 × años,
entonces "años" es una variable y "20" es un
parámetro.
Estadístico:
Censo o recuento de la población, de los
recursos naturales e industriales o de
cualquier otra manifestación o actividad de
un Estado, provincia, pueblo, clase.

4. Censo:
Para Levin & Rubin (1996) "Algunas veces es
posible y práctico examinar a cada persona o
elemento de la población que deseamos describir.
A esto lo llamamos una numeración completa o
censo. Utilizamos el muestre cuando no es posible
contar o medir todos los elementos de la
población. Ejemplo: Cuando se desea saber la
cantidad de personas que viven en un población
determinada.
Encuesta:
La encuesta, es un método mediante el cual
se quiere averiguar. Se efectúa a través de
cuestionarios verbales o escritos que son
aplicados a un gran número de personas.
Ejemplo: Cuando se desea saber el
favoritismo de un candidato político.

5. Estadística
Frecuencia
Descriptiva
Inferencial
Dividida en:
Resumen
Técnicas para
sacar los
resultados
Descriptiva
Recolectar
información

6. Los métodos estadísticos tradicionalmente se utilizan para propósitos
descriptivos, para organizar y resumir datos numéricos. La estadística
descriptiva, por ejemplo trata de la tabulación de datos, su presentación
en forma gráfica o ilustrativa y el cálculo de medidas descriptivas.
Ahora bien, las técnicas estadísticas se aplican de manera amplia en
mercadotecnia, contabilidad, control de calidad y en otras actividades;
estudios de consumidores; análisis de resultados en deportes;
administradores de instituciones; en la educación; organismos políticos;
médicos; y por otras personas que intervienen en la toma de decisiones.
Podemos decir que la función principal de la estadística es justamente la
recolección y agrupamiento de datos de diverso tipo para construir con
ellos informes estadísticos que nos den idea sobre diferentes y muy
variados temas, siempre desde un punto de vista cuantitativo y no
cualitativo.

9. Variable Cualitativa:
Son aquellas que no aparecen en forma numérica, sino como categorías o atributos
(sexo, profesión, color de ojos) y sólo pueden ser nominales u ordinales.
a) Nominales: Solo permite la clasificación, no se puede establecer ningún tipo de
orden. Ejemplo: Nacionalidad, sexo.
b) Ordinales: Hay una clasificación con cierto orden natural. Hay diferencia de grado. Se
habla de grado de estudio, nivel de educación, entre otras.
Variable Cuantitativa:
Son las variables que se expresan mediante cantidades numéricas. Las variables
cuantitativas además pueden ser:
a) Variable discreta: Es la variable que presenta separaciones o interrupciones en la
escala de valores que puede tomar. Estas separaciones o interrupciones indican la
ausencia de valores entre los distintos valores específicos que la variable pueda
asumir. Un ejemplo es el número de hijos.
b) Variable continua: Es la variable que puede adquirir cualquier valor dentro de un
intervalo especificado de valores. Por ejemplo el peso o la altura, que solamente está
limitado por la precisión del aparato medidor, en teoría permiten que siempre existe un
valor entre dos cualesquiera.