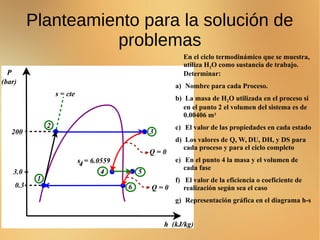
1. Se presenta un problema clásico de termodinámica que involucra un ciclo termodinámico con H2O como sustancia de trabajo. Se pide determinar varias propiedades del sistema en cada estado, así como los valores de trabajo, calor y eficiencia del ciclo. 2. Se recomienda organizar la información en una tabla y realizar cálculos de interpolación para determinar propiedades donde se requiera. 3. El análisis del ciclo involucra 6 procesos identificados y el cálculo de las propied

1. Planteamiento para la solución de
problemas
En el ciclo termodinámico que se muestra,
utiliza H2O como sustancia de trabajo.
Determinar:
a) Nombre para cada Proceso.
b) La masa de H2O utilizada en el proceso si
en el punto 2 el volumen del sistema es de
0.00406 m3
c) El valor de las propiedades en cada estado
d) Los valores de Q, W, DU, DH, y DS para
cada proceso y para el ciclo completo
e) En el punto 4 la masa y el volumen de
cada fase
f) El valor de la eficiencia o coeficiente de
realización según sea el caso
g) Representación gráfica en el diagrama h-s

2. Se observa un problema clásico,
donde se nos presenta un
problema, en el cual se nos
proporciona toda la información
explicita en una gráfica
Antes que cualquier otra
cosa, convendría
descargar toda la
información.
Antes que cualquier otra
cosa, convendría
descargar toda la
información a una tabla.
Pues sabemos que
habiendo llenado dicha
tabla, lo que resta del
problema es solo simples
cálculos

3. Análisis de la gráfica
Primero identificamos
los puntos de estado
que nos proporcionen
la información de
forma directa
Particularmente en este
ejercicio, el primer y el
último puntos de estado
se encuentran sobre la
linea de saturación

4. Sabemos que entre las lineas de
líquido saturado y vapor
saturado la temperatura y
(claramente) la presión son
constantes.
Y al estar los puntos de estado 1 y 6 a la misma presión, también
tienen la misma temperatura (TempSat(0.3 bar)
), por lo tanto les
corresponden las propiedades del líquido saturado y vapor
saturado respectivamente.
Sabemos que entre las lineas de
líquido saturado y vapor
saturado la temperatura y
(claramente) la presión son
constantes.
Isoterma (TempSat(0.3 bar)
)

5. Datos líquido saturado
(Azul) Datos vapor saturado
(Rojo)
Pagina 10 tablas

6. Nuestra tabla se encuentra de la siguiente manera
El punto de estado dos se encuentra en la zona de líquido
comprimido, y como lo muestra la gráfica, el punto de estado 2,
tiene la misma magnitud de entropía que el punto de estado 1
Ahora, el punto de estado: 2

7. Es decir s2 = s1 = 0.9441 [ kJ / kg K ]
Con los datos de
P2 = 200 bar y
s2 = 0.9441 [ kJ / kg K ]
Vamos a la tabla de Líquido
comprimido Pag. (19 tablas)

8. Pag. (19 tablas)
Puesto que nuestro dato se encuentras entre dos valores de entropía
de la tabla, se debe interpolar cada una de las propiedades restantes
(T, v, u, h)

9. La interpolación se realiza por medio de la ecuación de una recta
que pasa por dos puntos (dichos puntos son los valores entre los que
se encuentra el valor del punto de estado 2
yi=
( y 2− y1)
(x 2−x 1)
( xi−x 1)+ y1
T 2=
(80−60)
(1.0623−0.8205)
(0.9441−0.8205)+60=70.2233
Para la temperatura quedaría
T 2=
(0.9441−0.8205)
(1.0623−0.8205)
(80−60)+60=70.2233
yi=
( xi−x 1)
(x2−x 1)
( y 2− y1)+ y 1Que es igual que

10. yi=
( y 2− y1)
(x 2−x 1)
( xi−x 1)+ y1 yi=
( xi−x 1)
(x2−x 1)
( y 2− y1)+ y 1
La expresión de la derecha es igual a la de la izquierda, salvo que, como se puede
observar la división de la derecha no cambia y por lo tanto basta obtenerlo una vez.
T 2=
(0.9441−0.8205)
(1.0623−0.8205)
(80−60)+60=70.2233
T 2=0.511166(80−60)+60=70.2233
Por lo tanto para las demás propiedades, quedaría:
v 2=0.511166(0.00102−0.00101)+0.00101=0.001015[m3/ kg]
u2=0.511166(330.38−247.66)+247.66=289.9436[kJ /kg]
h2=0.511166(350.78−267.82)+267.82=310.22[kJ /kg]

11. El proceso 3 a 4 es Adiabático y por lo tanto isoentropico s3 = s4
El punto de estado 3, se encuentra en la
zona de vapor sobre calentado. (pag. 17)
P3 = 200 bar y
S3 = 6.0559 kJ / kg K
La lectura es
directa

12. La tabla de datos queda de la siguiente manera
El punto 4 se encuentra en la zona de Mezcla a 3 bar, para el cálculo
de las propiedades, ya que se conoce el valor de la entropía de la
mezcla se calcula la calidad y la humedad
x=
s4−sf
sg−sf
=
6.0559−1.6717
6.9916−1.6717
=0.824113
h=1−0.824113=0.175886

13. Ya conociendo la calidad y la humedad se calculan las demás
propiedades con los datos de la zona de mezcla a 3 bar (pag 10
Tablas)
v4=vg x−vf h=(0.60576∗0.8241)+(0.001073∗0.17588)=0.4994[m3/ kg]
u4=ug x−uf h=2194.57[kJ /kg]
h4=hg x−hf h=2344.37[kJ /kg]
La tabla ahora se ve de la siguiente manera

14. El proceso de 5 a 6, también es adiabático (isoentropico )
S5 = s6 = 7.7675 [kJ/ kg K]
P5 = 3 bar
S5 = 7.7675 [kJ/ kg K]
Zona Vapor sobre calentado
(pag 13 tablas)
7.7675

15. El mismo Procedimiento de interpolación que en el punto 2
yi=
( xi−x 1)
(x2−x 1)
( y 2− y1)+ y 1
T5=
(7.7675−7.7037)
(7.7738−7.7037)
(320−300)+300=318.2025o
C
v5=0.910128(0.90672−0.87534)+0.87534=0.90389[m3/kg]
u5=0.910128(2836.41−2806.98)+2806.98=2833.76[kJ /kg]
h5=0.910128(3110.43−3069.58)+3069.58=3106.75[kJ /kg]

16. 1 2 La presión aumenta a entropía constante
Compresión Adiabática
La tabla ya está completa y solo resta realizar los cálculos
Nombre de cada proceso
2 3 La temperatura aumenta a presión constante
Calentamiento Isobárico
3 4 El volumen aumento sin desprendimiento de calor
Expansión Adiabática
4 5 La temperatura aumenta a presión constante
Calentamiento Isobárico
5 6 El volumen aumento sin desprendimiento de calor
Expansión Adiabática
6 1 Pasa de vapor saturado a líquido saturado
Condensación Isobárica (Condensación Isotérmica)

17. 1 2 La presión aumenta a entropía constante
Compresión Adiabática
ΔU1−2=m(u2−u1)
ΔH1−2=m(h2−h1)
ΔS1−2=m(s2−s1)
ΔU1−2=Q1−2+W1−2 Q1−2=0
W1−2=ΔU1−2
2 3 La temperatura aumenta a presión constante
Calentamiento Isobárico
Cálculo de la masa
En el inciso b) indica que en el punto 2 el volumen total es de 0.00406 m3
por lo tanto se utiliza ese estado para calcular la masa.
m=
0.00406m
3
0.001015
m
3
kg
=4kg
ΔU2−3=m(u3−u2)
ΔH2−3=m(h3−h2)
ΔS2−3=m(s3−s2)
Q2−3=Δ H2−3
W2−3=ΔU2−3−Q2−3

18. 3 4 El volumen aumento sin desprendimiento de calor
Expansión Adiabática
4 5 La temperatura aumenta a presión constante
Calentamiento Isobárico
ΔU3−4=m(u4−u3)
ΔH3−4=m(h4−h3)
ΔS3−4=m(s4−s3)
Q3−4=0
W3−4=ΔU3−4
ΔU4−5=m(u5−u4)
ΔH4−5=m(h5−h4)
ΔS4−5=m(s5−s4)
Q4−5=Δ H4−5
W4−5=ΔU4−5−Q4−5
5 6 El volumen aumento sin desprendimiento de calor
Expansión Adiabática
ΔU5−6=m(u6−u5)
ΔH5−6=m(h6−h5)
ΔS5−6=m(s6−s5)
Q5−6=0
W5−6=ΔU5−6

19. 6 1 Pasa de vapor saturado a líquido saturado
Condensación Isobárica (Condensación Isotérmica)
ΔU6−1=m(u1−u6)
ΔH6−1=m(h1−h6)
ΔS6−1=m(s1−s6)
Q6−1=Δ H6−1
W6−1=ΔU6−1−Q6−1

20. 6 1 Pasa de vapor saturado a líquido saturado
Condensación Isobárica (Condensación Isotérmica)
ΔU6−1=m(u1−u6)
ΔH6−1=m(h1−h6)
ΔS6−1=m(s1−s6)
Q6−1=Δ H6−1
W6−1=ΔU6−1−Q6−1

21. Como el Calor Total QT = 5161.64 kJ es positivo, entonces es una
Maquina Térmica
η=
W
Qpositivo
=
5161.64kJ
14502.56kJ
=0.3559
Para el punto 4 la masa de la fase vapor es igual al producto de la masa
total (m) por la calidad (x)
mvapor=m x=4kg(0.824113)=3.2964kg
mlíquido=m−mvapor=0.7035kg
Para el punto 4 el volumen de la fase vapor es igual al producto del
volumen especifico por la masa del vapor
Vvapor=v4 mvapor=(0.4994
m3
kg
)3.2964kg=1.6462m
3
Vlíquido=(0.4994
m3
kg
)0.7035kg=0.3513m
3
%Vvapor=82.41
%Vlíquido=17.59