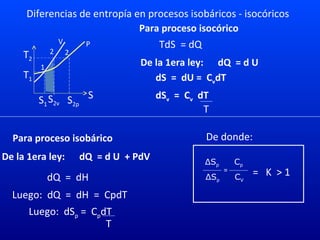
Este documento trata sobre el cambio de entropía en una sustancia pura. Explica que la entropía es una medida de la transformación de energía en mecánica según la segunda ley de la termodinámica. Describe diferentes procesos termodinámicos como isotérmicos, isobáricos e isentrópicos y cómo afectan al cambio de entropía. También presenta cuatro problemas de cálculo relacionados con el cambio de entropía en procesos termodinámicos.

1. CAMBIO DE ENTROPIA EN UNA
SUSTANCIA PURA
UNIVERSIDAD TEGNOLOGICA
DEL CONO SUR
M.Sc. Ing. Rita Cabello T.http://experto-ptc.blogspot.com

2. ENTROPIA
Es una medida de la transformación de la energía en mecánica.
Surge como un postulado de la 2da ley de la termodinámica y se
establece a partir de la desigualdad de Clausius.
Considerando 2 ciclos reversibles formados por trayectorias A, B y C:
T
V
1
2A
B
C
Para el ciclo formado por las
trayectorias A y B:
dQ
T
= 0
dQ
T
= 0
1A
2A
+
T
2B
1B
dQ … ( α)
dQ
T
= 0
1A
2A
+
T
2C
1C
dQ … ( ϐ)
TRAYECTORIAS A Y B TRAYECTORIAS A Y C

3. Sumando ( α) - ( ϐ):
T
2B
1B
dQ
= 0-
T
2C
1C
dQ
T
2B
1B
dQ
= cte=
T
2C
1C
dQ
El término es independiente de la trayectoria. Clausius lo
denominó «entropia»
T
dQ
T
dQ rev = 0
T
dQ
=dS
rev
Entropía: (desorden, caos molecular)
Unidades: Joule/ºC, BTU/ºF, cal/ºC

4. Unidades: Joule/Kg ºC, BTU/lb ºF, cal/g ºC
Entropía: por unidad de masa:
T
dQ=ΔS
rev
S = Sf + x Sfg
Para una mezcla difásica:
; Sfg = Sg - Sf
Sf = entropía específica Liquido saturado
Sg = entropía específica vapor saturado
Sf y Sg de Tablas de vapor saturado
Diagrama de calor
De la 2da ley:
Si el proceso es de 1 -2,
S2>S1, ΔS = (+)
T
dQ
=dS
dST = dQ = Area
T = QΔSdS S2S1
T1
T2
2
1
S
luego: Q = (+)
Si el proceso es de 2 -1,
S2>S1, ΔS = (-)
luego: Q = (-)

5. Proceso
isotérmico
dS = dQ = Area
S2S1
T1
T2
2
1
S
T
S2S1
T 2
S
Q
1
Proceso isobárico
P
De la 1era ley:
dQ - dW = d U
dQ = d U + dW = ( d ( U + PV)
dQ = d H
dS = dQ = d HT
T = ΔHΔS

6. Proceso isocórico
dQ - dW = dU
S2S1
T1
T2
1
S
Proceso adiabático
P2 De la 2da ley:
S1 = S2
dS = dQ = d H
Es un proceso isentrópico
S2S1
T1
T2
2
1
S
V
ΔU
De la 1era ley:
dW - PdV = 0
dQ = d U
2
P1
Qp
>
Qp = Calor generado por la
disipación
dS = dQ = 0T
ΔS = 0

7. Proceso isentrópico
S2S1
T1
T2
1
S
Proceso politrópico
P2
De la 1era ley:
T
S
1
S1≠ S2≠ S3≠ S4≠ S5≠ S6≠ S7≠ S8≠ S9≠ S10
2
P1
dQ – dW = dU
P, T, V cambian
0
8
6
4
2 3
5
7
9
Por lo tanto «todo proceso adiabático
reversible es isotrópico, pero no todo proceso
isotrópico es adibático reversible»
V2
V1
De la 2da ley:
TdS = dQ
TdS = Area=Q
=ΔS

12. Para proceso isocórico
dQ = dH
TdS = dQ
Diferencias de entropía en procesos isobáricos - isocóricos
S2pS1
T1
T2
2
1
S
V P
2
S2v
De la 1era ley: dQ = d U
dS = dU = CvdT
dSv = Cv dT
T
Para proceso isobárico
De la 1era ley: dQ = d U + PdV
Luego: dQ = dH = CpdT
Luego: dSp = CpdT
T
De donde:
ΔSp
ΔSp
=
Cp
CV
= K > 1

14. Problema 1:
Una maquina térmica que opera con un ciclo reversible de Carnot toma energía de un
deposito térmico de temperatura alta y cuenta con una eficiencia térmica de 57.89%
produciendo 2932 J de trabajo en cada ciclo. Si el calor rechazado va el entorno que se
encuentra a 27ºC determinar: a) la temperatura en ºC del deposito térmico de
temperatura alta.
b) Si la maquina cumple con la desigualdad de Clausius. Justifique matemáticamente su
respuesta.

16. Problema 2:

18. Problema 3:

22. Problema 4:
Aire a 10 bar y 200ºC se expande adiabáticamente hasta 1 bar y
100ºC.
a) determine si el exceso es reversible, irreversible o imposible
b) Considerando que la expansión es adiabática reversible, cual
seria la temperatura de salida a 1 bar?. Si Cp u= 1,004 KJ/Kg ºK R =
0.287 KJ/Kg ºK.
Solución:
a) Calculo Δ S = Cp dT - R ln P2
P1T
Δ S = Cp ln T2/T1 - R ln P2 /P1
Δ S = 1,004 ln 373/473 – 0,287 ln 1/10 = 0,424 KJ /kg ºK
Por tanto: Proceso factible pero irreversible

23. b) Reversible adibatico
Δ S = 0 = Cp ln T2/T1 = R ln P2 /P1
T2/T1 = (P2 /P1 ) (R/Cp)
= (1/10) (0.287/1,004)
T2 = 473 x 0,5177 = 244,9ºC