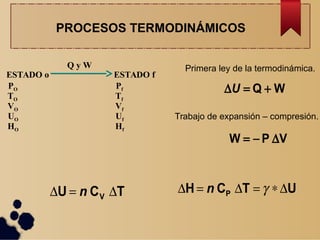
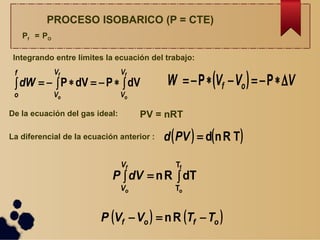
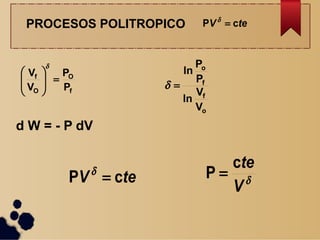
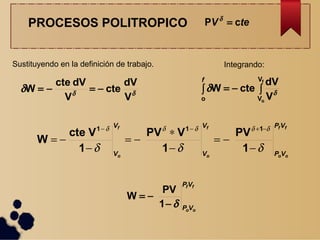
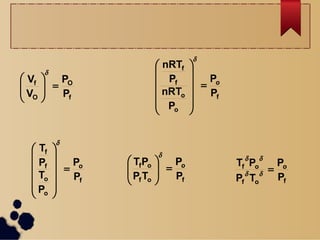
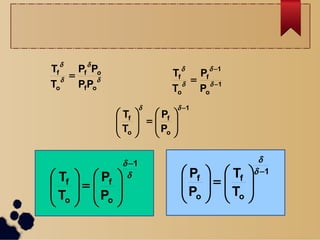
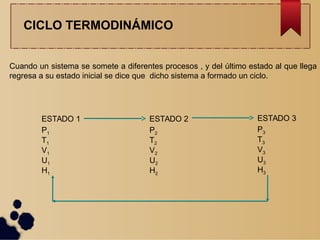
Este documento describe los diferentes procesos termodinámicos como isotérmicos, isobáricos, isocóricos y adiabáticos. Explica las ecuaciones que rigen cada proceso y cómo calcular el trabajo y la transferencia de calor. También define los ciclos termodinámicos y las máquinas térmicas y de refrigeración, incluida su eficiencia y coeficiente de rendimiento.

1. PROCESOS TERMODINÁMICOS
ESTADO o
PO
TO
VO
UO
HO
ESTADO f
Pf
Tf
Vf
Uf
Hf
Q y W
WQ U
Primera ley de la termodinámica.
VPW 
Trabajo de expansión – compresión.
TCU V  n UTCH P  n

2. PROCESOS ISOTERMICO (T = cte); Tf = TO
U = 0 H = 0
Q = – W
De la primera ley, nos queda
f
O
O
f
P
P
V
V

dVP dW
Matemáticamente la integral de esta ecuación nos da el área bajo la curva en
un diagrama P - V
V
P
 dW

3. PROCESOS ISOTERMICO (T = cte); Tf = TO
Como esta es una variable de trayectoria, para
su calculo dependerá del tipo de proceso que
se este llevando a cabo.
dVP dW
De la ecuación del gas ideal: PV = nRT
Por lo tanto:
V
TRn
P
Sustituyendo el valor de la presión en la ecuación del trabajo:
V
dV
TRn
V
dVTRn
dW

4. PROCESOS ISOTERMICO (T = cte); Tf = TO
V
dV
TRn
V
dV
TRn
f
o
f
o
V
V
V
Vo

f
dW
Integrando entre límites se tiene que:
V
V
lnTRn
o
f
W
De la ley de Boyle: VPVP ffoo  
P
P
V
V
f
o
o
f

f
o
o
f
P
P
lnTRn
V
V
lnTRn W
Kkmol
kJ
8.314
Kmol
J
8.314R 

5. PROCESOS ISOBARICO (P = cte); Pf = PO
O
f
O
f
V
V
T
T
 QH
W = U – QDe la primera ley, nos queda
 ofVV TTCTCU  nn
  Unn  ofPP TTCTCH

6. PROCESO ISOBARICO (P = CTE)
Pf = PO
dVPdVP  
f
o
f
o
V
V
V
V
f
o
dW
Integrando entre límites la ecuación del trabajo:
  PP VVVW of 
De la ecuación del gas ideal: PV = nRT
La diferencial de la ecuación anterior :    TRndPVd
   Rn ofof TTVVP 
dTRn
f
o
T
T

f
o
V
V
dVP

7.    RP ofof TTnVVW 
Pa ó kPa m3
J ó kJ
Kkmol
kJ
8.314
Kmol
J
8.314R 
PROCESO ISOBARICO (P = CTE)

8. PROCESOS ISOCORICO (V = cte); Vf = VO
o
f
O
f
P T
TP

Q = U
De la primera ley, nos queda
W = 0
dVPdW
 ofVV TTCTCU  nn

9. PROCESOS ADIABATICO (Q = 0);
0Q
W = U
De la primera ley, nos queda
 ofVV TTCTCU  nn

10. PROCESOS POLITROPICO
f
O
O
f
P
P
V
V







V
V
ln
P
P
ln
o
f
f
o

teV cP 

V
tec
P 
d W = - P dV
teV cP 

11. Sustituyendo en la definición de trabajo.


V
dV
cte
V
dVcte
W 
Integrando:

f
o
V
Vo V
dV
cteW 

f
ff
oo
f
o
f
o
VP
VP
V
V
V
V










1
PV
1
VPV
1
Vcte
W
111
ff
oo
VP
VP

1
PV
W
PROCESOS POLITROPICO teV cP 

12. Pero:
nRTPV
onRTooVP
fnRTffVP
f
o
T
T

1
nRT
W
 



1
TTnR
W of  
1
TTnR
W of




ó
f
O
O
f
P
P
V
V







f
f
o
o
f
f
o
o
O
f
V
T
V
T
V
nRT
V
nRT
V
V








13. of
fo
f
f
o
o
O
f
VT
VT
V
nRT
V
nRT
V
V







of
fo
o
f
VT
VT
V
V


of
fo
o
f
VV
VV
T
T



oo
ff
o
f
VV
VV
T
T









 1
o
1
f
o
f
V
V
T
T








1
o
f
o
f
V
V
T
T 







1
1
o
f
o
f
T
T
V
V

14. f
O
O
f
P
P
V
V







f
o
o
f
f
P
P
P
nRT
P
nRT
o














f
o
o
f
f
P
P
P
T
P
T
o














fof
of
P
P
TP
PT o







fof
of
P
P
TP
PT o



15. 



of
f
o
f
PP
PP
T
T o

1
o
1
f
o
f
P
P
T
T


 



1
o
f
o
f
P
P
T
T















 1
o
f
o
f
P
P
T
T












 1
o
f
o
f
T
T
P
P 











 


16. CICLO TERMODINÁMICO
Cuando un sistema se somete a diferentes procesos , y del último estado al que llega
regresa a su estado inicial se dice que dicho sistema a formado un ciclo.
ESTADO 1
P1
T1
V1
U1
H1
ESTADO 2
P2
T2
V2
U2
H2
ESTADO 3
P3
T3
V3
U3
H3

17. Así como para un proceso se determina los U, H, Q y W,
también para un ciclo se tienen que determinar.
0133221f   UUUUU oc
0133221f   HHHHH oc
0133221f   QQQQQ oc
0133221f   WWWWW oc
Qc (+)
Wc (–)
Máquina Térmica:

18. Máquina Térmica:
Es un dispositivo que al introducirle calor este se transforma en
trabajo. Pero como no toda la energía térmica se transforma, estas
operan con una eficiencia.
istradosuCalor
Eficiencia
min
ciclodeltrabajo

sumQ
cW

Es el calor o suma de calores positivos que
llevan a cabo en los diferentes procesos .
10 

19. Máquina Frigorífica
Es un dispositivo que transfiere energía de una zona de baja
temperatura a una de alta, mediante la introducción de un trabajo o
potencia.
ciclodeltrabajo
min
nrealizacióde
istradosuCalor
eCoeficient 
Wc
sumQ

Es el calor o suma de calores positivos que
llevan a cabo en los diferentes procesos .
0
Qc (–)
Wc (+)
Máquina Frigorífica: