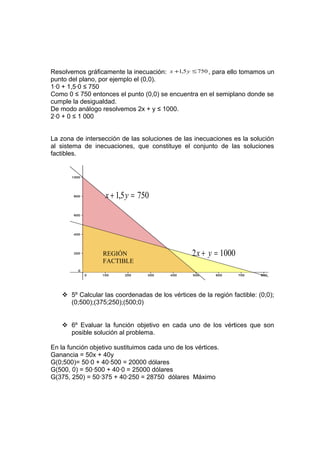
El fabricante puede confeccionar un máximo de 375 pantalones y 250 camperas para obtener una ganancia máxima de $28,750. Para resolver este problema de programación lineal, se identificaron las variables, se establecieron las restricciones de materiales y la función objetivo de ganancia, se representó gráficamente la región factible, y se evaluó la función objetivo en los vértices para encontrar la solución óptima.

1. 






≥
≥
≤+
≤+
0
0
10002
7505,1
y
x
yx
yx
COMO RESOLVER UN PROBLEMA DE
PROGRAMACIÓN LINEAL
Ejemplo:
Una tienda deportiva encarga a un fabricante pantalones y camperas. El
fabricante dispone para la confección de 750 m de tejido de algodón y 1000m
de tejido de poliéster. Cada pantalón precisa 1m de algodón y 2m de
poliéster. Cada campera precisa 1,5m de algodón y am de polieste.
El precio del pantalón se fija en 50 dólares y el de la campera en 40
dólares. ¿Qué número de pantalones y camperas debe suministrar el
fabricante a la tienda para que ésta consiga una ganancia máxima?
 1º Elección de la incógnita x = número de pantalones
y = número de chaquetas
 2º Escribo la Función objetivo: Ganancia= 50x + 40y
 3º Escribo las restricciones del problema (Puedo ayudarme
elaborando una tabla donde ordeno los datos.)
 4º Hallar el conjunto de soluciones factibles
Se representan gráficamente las soluciones. Al ser x ≥ 0 e y ≥ 0, se trabaja
en el primer cuadrante. Representamos las rectas, a partir de sus puntos de
corte con los ejes.
pantalones campera disponible
algodón 1m 1,5m 750m
poliéster 2m 1m 1000m

2. Resolvemos gráficamente la inecuación: 7505,1 ≤+ yx , para ello tomamos un
punto del plano, por ejemplo el (0,0).
1·0 + 1,5·0 ≤ 750
Como 0 ≤ 750 entonces el punto (0,0) se encuentra en el semiplano donde se
cumple la desigualdad.
De modo análogo resolvemos 2x + y ≤ 1000.
2·0 + 0 ≤ 1 000
La zona de intersección de las soluciones de las inecuaciones es la solución
al sistema de inecuaciones, que constituye el conjunto de las soluciones
factibles.
 5º Calcular las coordenadas de los vértices de la región factible: (0;0);
(0;500);(375;250);(500;0)
 6º Evaluar la función objetivo en cada uno de los vértices que son
posible solución al problema.
En la función objetivo sustituimos cada uno de los vértices.
Ganancia = 50x + 40y
G(0;500)= 50·0 + 40·500 = 20000 dólares
G(500, 0) = 50·500 + 40·0 = 25000 dólares
G(375, 250) = 50·375 + 40·250 = 28750 dólares Máximo
10002 =+ yx
7505,1 =+ yx
REGIÓN
FACTIBLE

3.  7º Interpretar los resultados obtenidos y escribir la respuesta al
problema.
La solución óptima es fabricar 375 pantalones y 250 camperas para
obtener un beneficio de 28750 dólares.