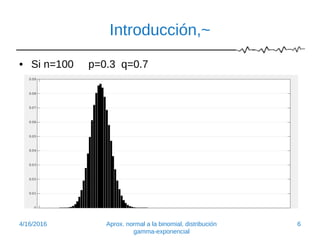
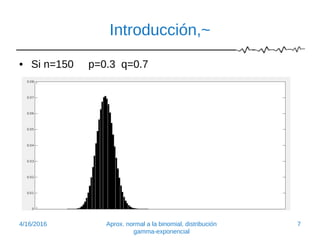
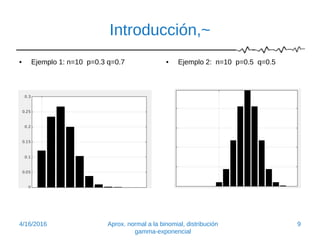
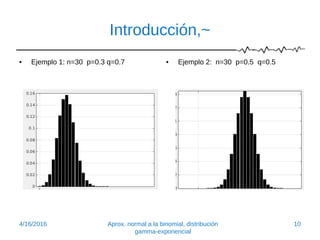
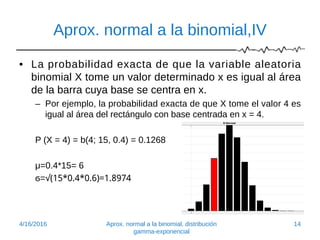
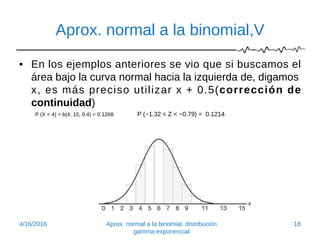
Este documento introduce la aproximación normal a la distribución binomial. Explica que cuando el tamaño de la muestra (n) es grande y la probabilidad de éxito (p) no está extremadamente cerca de 0 o 1, la distribución normal proporciona una buena aproximación. Presenta ejemplos para ilustrar cómo la distribución binomial se aproxima a la normal a medida que n aumenta o p se acerca a 1/2. También muestra cómo calcular probabilidades binomiales usando áreas bajo la curva normal.

1. APROXIMACIÓN NORMAL A LA
BINOMIAL
FCC BUAP
Luis Alfredo Moctezuma
4/16/2016 1Aprox. normal a la binomial, distribución
gamma-exponencial

2. Introducción,I
• Conocerémos la relación entre la distribución binomial y
la normal
– Se sabe que algunas distribuciones convergen a la normal a
medida que sus parámetros se aproximan a ciertos límites.
• Cuando n es considerablemente grande
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
2

3. Introducción,~
• Distribución binomial
– dos resultados posibles: éxito,fracaso
– n: tamaño de muestra
– p: probabilidad de éxito
– q=1-p: probabilidad de fracaso
• Distribución normal
– μ: media de la población μ=np
– σ: desviacion estandar de la población σ=√(n.p.q)
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
3

4. Introducción,~
- Si n=5 p=0.3 q=0.7
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
4
- Si n=10 p=0.3 q=0.7
Ejemplo de distribución binomial: p=0.3 q=0.7

5. Introducción,~
• Si n=30 p=0.3 q=0.7
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
5

6. Introducción,~
• Si n=100 p=0.3 q=0.7
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
6

7. Introducción,~
• Si n=150 p=0.3 q=0.7
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
7

8. Introducción,~
• Ejemplo 1: n=5 p=0.3 q=0.7 • Ejemplo 2: n=5 p=0.5 q=0.5
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
8

9. Introducción,~
• Ejemplo 1: n=10 p=0.3 q=0.7 • Ejemplo 2: n=10 p=0.5 q=0.5
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
9

10. Introducción,~
• Ejemplo 1: n=30 p=0.3 q=0.7 • Ejemplo 2: n=30 p=0.5 q=0.5
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
10

11. Aproximación normal a la binomial,I
• La distribución normal con μ=np y σ2= npq ofrece una
muy buena aproximación cuando:
– n es grande y p no esta extremadamente cerca de 0 o 1
– n es pequeña pero p esta razonablemente cerca de 1/2
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
11

12. Aprox. normal a la binomial,II
Teorema 6.3:
Si X es una variable aleatoria binomial con media μ = np
y desviación estandar σ= √(npq), entonces la forma
limitante de la distribución de
conforme n--> ∞, es la distribución normal estandar
Permitirá utilizar áreas bajo la curva normal para
aproximar propiedades binomiales cuando n es
suficientemente grande.
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
12

13. Aprox. normal a la binomial,III
• Estadístico Z
– Mide la distancia entre un valor especificado de X y la media
aritmética, en las unidades de la desviación estándar(normaliza)
– Al determinar el valor Z, se puede encontrar el área de
probabilidad bajo cualquier curva normal
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
13

14. Aprox. normal a la binomial,IV
• La probabilidad exacta de que la variable aleatoria
binomial X tome un valor determinado x es igual al área
de la barra cuya base se centra en x.
– Por ejemplo, la probabilidad exacta de que X tome el valor 4 es
igual al área del rectángulo con base centrada en x = 4.
P (X = 4) = b(4; 15, 0.4) = 0.1268
μ=0.4*15= 6
ϭ=√(15*0.4*0.6)=1.8974
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
14

15. Aprox. normal a la binomial,IV,~
• Que es aproximadamente igual al área de la región
sombreada bajo la curva normal entre las dos
ordenadas x1= 3.5 y x2= 4.5
P (X = 4 ) = b(4; 15, 0.4) ≈ P (−1.32 < Z < −0.79)
= P (Z <−0.79) − P (Z < −1.32) = 0.2148 − 0.0934
= 0.1214
0.1268 ≈ 0.1214
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
15

16. Aprox. normal a la binomial,IV,~
• La probabilidad de que X tome un valor de 7 a 9 es dada
por:
= 0.9662 − 0.6098 = 0.3564
– Que es igual a la sumatoria de las áreas de los rectángulos
cuyas bases están centradas en x = 7, 8 y 9
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
16

17. Aprox. normal a la binomial,IV,~
• Para la aproximación normal calculamos el área de la
región sombreada bajo la curva entre las ordenadas
x1=6.5 y x2=9.5
• P (7 ≤ X ≤ 9) ≈ P ( 0.26 < Z < 1.85) = P (Z < 1.85) − P (Z < 0.26)
= 0.9678 − 0.6026 = 0.3652
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
17

18. Aprox. normal a la binomial,V
• En los ejemplos anteriores se vio que si buscamos el
área bajo la curva normal hacia la izquierda de, digamos
x, es más preciso utilizar x + 0.5(corrección de
continuidad)
P (X = 4) = b(4; 15, 0.4) = 0.1268 P (−1.32 < Z < −0.79) = 0.1214
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
18

19. Aprox. normal a la binomial,VI
• Sea X una variable aleatoria binomial con parámetros n
y p. Para una n grande, X tiene aproximadamente una
distribución normal con μ= np y σ= √(npq)
» ≈ área bajo la curva normal a la izq de x+0.5
y la aproximación será buena si np y nq son mayores que o
iguales a 5
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
19

20. Aprox. normal a la
binomial,VII,Ejemplo1
• Un paciente que padece una rara enfermedad de la
sangre tiene 0.4 de probabilidad de recuperarse.
Si se sabe que 100 personas contrajeron esta
enfermedad, ¿cuál es la probabilidad de que sobrevivan
menos de 30?
– n es grande
– p esta relativamente cerca de 1/2
μ=100*0.4= 40
σ=√(100*0.4*0.6)=4.899
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
20

21. Aprox. normal a la
binomial,VII,Ejemplo1,~
• Para obtener la probabilidad que se desea, tenemos que
calcular el área a la izquierda de x = 29.5
• P (X < 30) ≈ P (Z <−2.14) = 0.0162
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
21

22. Aprox. normal a la
binomial,VII,Ejemplo2
• Un examen de opción múltiple tiene 200 preguntas,
cada una con 4 respuestas posibles, de las que sólo una
es la correcta. ¿Cuál es la probabilidad de que
solamente adivinando se obtengan de 25 a 30
respuestas correctas para 80 de los 200 problemas
sobre los que el estudiante no tiene conocimientos?
μ=80*1/4= 20
σ=√(80*1/4*3/4)=3.873
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
22

23. Aprox. normal a la
binomial,VII,Ejemplo2,~
• Se necesita el área entre x1 = 24.5 y x2 = 30.5. Los
valores z correspondientes son
≈ P (1.16 < Z < 2.71)
= P (Z < 2.71) − P (Z < 1.16) = 0.9966 − 0.8770 = 0.1196
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
23

24. Aprox. normal a la
binomial,VII,Ejemplo3
• La probabilidad de que cierta clase de componente
sobreviva a una prueba de choque es de 3/4. Calcule la
probabilidad de que sobrevivan exactamente 2 de los
siguientes 4 componentes que se prueben.
μ=4*3/4= 3
σ=√(4*3/4*1/4)=0.75
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
24

25. Aprox. normal a la
binomial,VII,Ejemplo3,~
• Se necesita el área entre x1 = 1.5 y x2 = 2.5. Los
valores z correspondientes son
=0.2109
• ≈ P (-2 < Z < -0.66) = P (Z < -0.66) − P (Z < -2)
= 0.2877- 0.0228 = 0.2649
4/16/2016 Aprox. normal a la binomial, distribución
gamma-exponencial
25