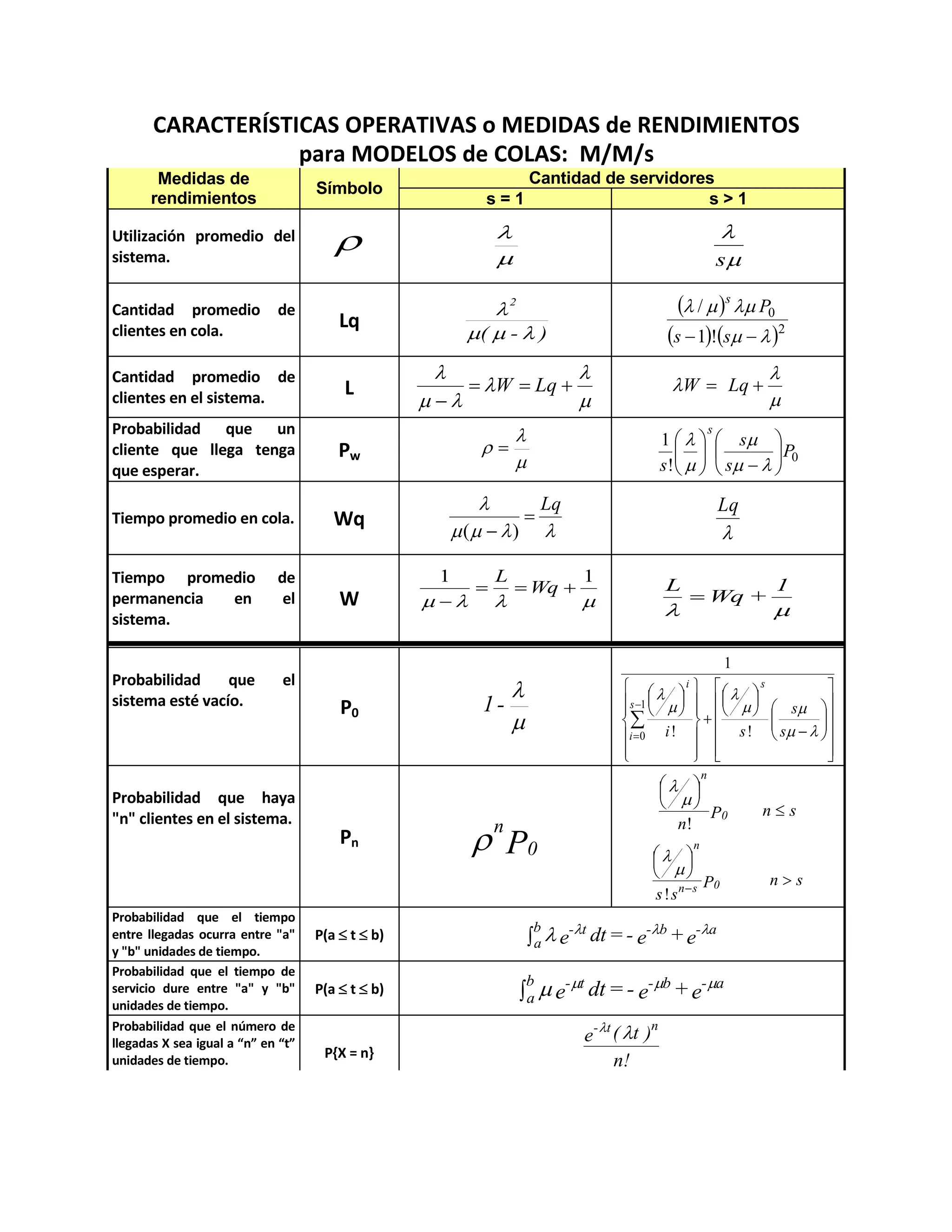
Este documento resume las medidas de rendimiento y probabilidades clave para modelos de colas M/M/s. Incluye la utilización promedio del sistema, la cantidad promedio de clientes en cola y en el sistema, la probabilidad de que un cliente tenga que esperar, y las probabilidades de que el sistema esté vacío o contenga un cierto número de clientes.

1. CARACTERÍSTICAS OPERATIVAS o MEDIDAS de RENDIMIENTOS
para MODELOS de COLAS: M/M/s
Medidas de Cantidad de servidores
Símbolo
rendimientos s=1 s>1
Utilización promedio del
sistema.
 


s
Cantidad promedio de 2  /  s  P0
Lq
clientes en cola. (  -  ) s  1!s   2
Cantidad promedio de   
L  W  Lq  W  Lq 
clientes en el sistema.    
Probabilidad que un  s
 1     s 
cliente que llega tenga Pw     P0
que esperar.  s !     s   
 Lq Lq
Tiempo promedio en cola. Wq 
 (   )  
Tiempo promedio de 1 L 1
  Wq  L 1
permanencia en el W      Wq +
sistema.
 
1
Probabilidad que el
   
s 1   
i     s
   

sistema esté vacío. P0 1-        s 
     s   
 
i 0 i !   s!  

  
  

n
 
 
Probabilidad que haya  
"n" clientes en el sistema. P0 ns
 P0
n n!
Pn n
 
 
  ns
P0
s ! sns
Probabilidad que el tiempo
-t
entre llegadas ocurra entre "a" P(a  t  b) a  e
b
dt = - e-b + e-a
y "b" unidades de tiempo.
Probabilidad que el tiempo de
- t
servicio dure entre "a" y "b" P(a  t  b) a  e
b
dt = - e- b + e- a
unidades de tiempo.
e - t ( t )
Probabilidad que el número de n
llegadas X sea igual a “n” en “t”
P{X = n}
unidades de tiempo. n!