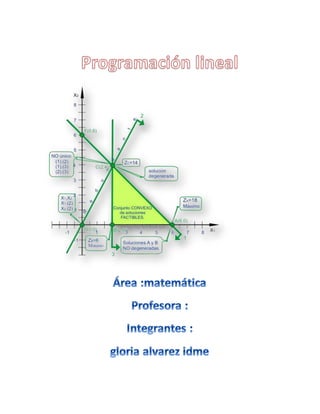
La programación lineal estudia las situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, llamadas restricciones. Consiste en optimizar una función objetivo lineal sujeta a restricciones también lineales. El conjunto de soluciones factibles satisface todas las restricciones simultáneamente.