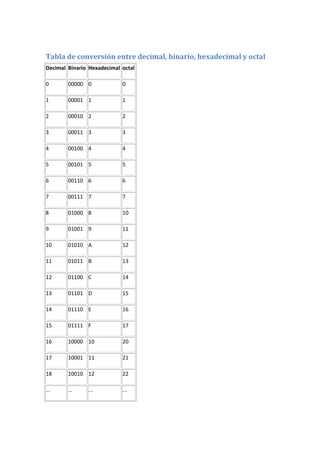
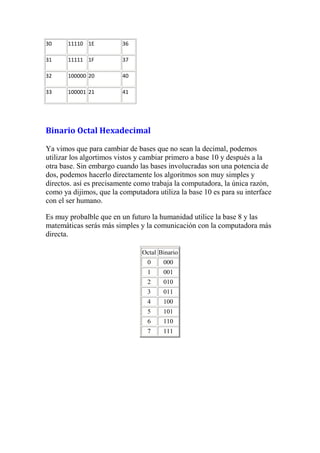
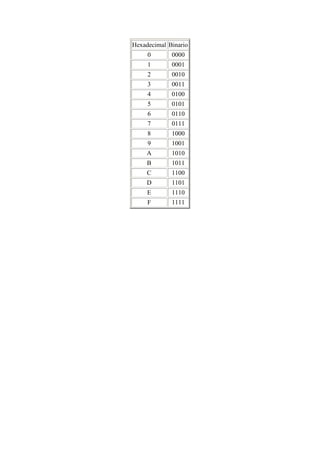
El documento explica los sistemas de numeración binario, decimal, hexadecimal y octal. El sistema binario representa números utilizando solo los dígitos 0 y 1 y es el sistema utilizado por las computadoras. Se describen métodos para convertir entre estos sistemas de numeración, incluyendo dividir números sucesivamente entre la base del sistema y anotar los restos o multiplicar dígitos por potencias de la base. También se explican operaciones como suma y resta en los sistemas hexadecimal y octal.

1. El sistema binario
En matemáticas e informática es un sistema de numeración en el que los números se
representan utilizando solamente las cifras cero y uno (0 y 1). Es el que se utiliza en las
computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo
cual su sistema de numeración natural es el sistema binario (encendido 1, apagado
0).
Decimal a binario
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a
dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2.
Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero,
simplemente se colocan en orden inverso a como aparecen en la división, se les da la
vuelta
Otra forma de conversión consiste en un método parecido a la factorización en números
primos. Es relativamente fácil dividir cualquier número entre 2. Este método consiste también
en divisiones sucesivas. Dependiendo de si el número es par o impar, colocaremos un cero o
un uno en la columna de la derecha. Si es impar, le restaremos uno y seguiremos dividiendo
entre dos, hasta llegar a 1. Después sólo nos queda tomar el último resultado de la columna
izquierda (que siempre será 1) y todos los de la columna de la derecha y ordenar los dígitos de
abajo a arriba
Suma de números binarios
La tabla de sumar para números binarios es la siguiente:
+ 0 1
0 0 1
1 0 10

2. El sistema Hexadecimal (no confundir con sistema sexagesimal), a veces abreviado como Hex,
—empleando por tanto 16 símbolos—. Su uso actual está muy vinculado a la informática y
ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como
unidad básica de memoria; y, debido a que un byte representa 28 valores posibles, y esto
puede representarse como
Operaciones en Sistema Hexadecimal
En el sistema hexadecimal, al igual que en el sistema decimal, binario y octal, se pueden
hacer diversas operaciones matemáticas. Entre ellas se encuentra la resta entre dos
números en sistema hexadecimal, la que se puede hacer con el método de complemento
a 15 o también utilizando el complemento a 16. Además de éstas, debemos manejar
adecuadamente la suma en sistema hexadecimal, explicada a continuación:
Hexadecimal Decimal
A 10
B 11
C 12
D 13
E 14
F 15
Sistema octal
El sistema numérico en base 8 se llama octal y utiliza los dígitos 0 a 7.
Para convertir un número en base decimal a base octal se divide por 8
sucesivamente hasta llegar a cociente 0, y los restos de las divisiones en
orden inverso indican el número en octal. Para pasar de base 8 a base
decimal, solo hay que multipicar cada cifra por 8 elevado a la posición de
la cifra, y sumar el resultado

3. Tabla de conversión entre decimal, binario, hexadecimal y octal
Decimal Binario Hexadecimal octal
0 00000 0 0
1 00001 1 1
2 00010 2 2
3 00011 3 3
4 00100 4 4
5 00101 5 5
6 00110 6 6
7 00111 7 7
8 01000 8 10
9 01001 9 11
10 01010 A 12
11 01011 B 13
12 01100 C 14
13 01101 D 15
14 01110 E 16
15 01111 F 17
16 10000 10 20
17 10001 11 21
18 10010 12 22
... ... ... ...

4. 30 11110 1E 36
31 11111 1F 37
32 100000 20 40
33 100001 21 41
Binario Octal Hexadecimal
Ya vimos que para cambiar de bases que no sean la decimal, podemos
utilizar los algortimos vistos y cambiar primero a base 10 y después a la
otra base. Sin embargo cuando las bases involucradas son una potencia de
dos, podemos hacerlo directamente los algoritmos son muy simples y
directos. así es precisamente como trabaja la computadora, la única razón,
como ya dijimos, que la computadora utiliza la base 10 es para su interface
con el ser humano.
Es muy probalble que en un futuro la humanidad utilice la base 8 y las
matemáticas serás más simples y la comunicación con la computadora más
directa.
Octal Binario
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111

5. Hexadecimal Binario
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111