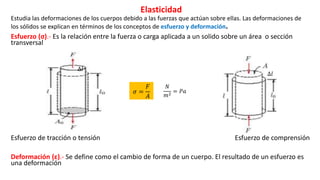
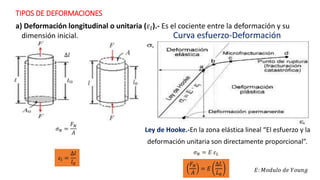
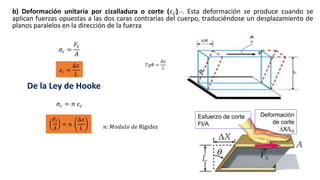
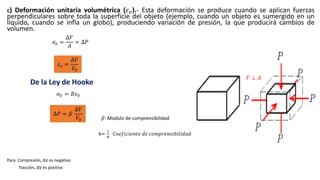
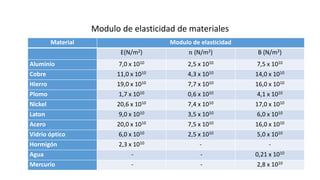
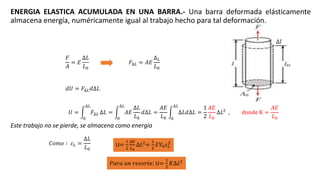
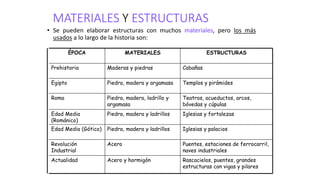
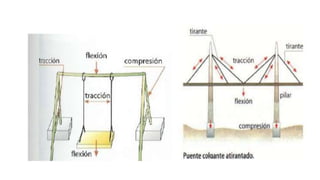
Este documento introduce conceptos básicos de elasticidad como esfuerzo, deformación y leyes de Hooke. Explica tipos de deformación como longitudinal, de corte y volumétrica. Describe cómo se miden y relacionan estos conceptos. También presenta ejemplos de módulos de elasticidad para diferentes materiales y cómo almacenan energía estructuras deformadas elásticamente.

1. FACULTAD DE INGENIERIA MECANICA Y ELECTRICA
ESCUELA DE INGENIERIA MECANICA Y ELECTRICA
DECANO : DR. MARTIN ALARCON
CURSO : FISICA II
DOCENTE : Mag. Carlos HUARCAYA CARHUAYO

2. ELASTICIDAD-INTRODUCCION
• Todo cuerpo sobre el que actúan fuerzas externas sufre una deformación que depende de la
naturaleza del sólido y de las fuerzas que sobre él actúan.
• Si al suprimir las fuerzas que actúan sobre el sólido este vuelve a recobrar su estado original se
dice que es elástico. (Las deformaciones que se producen son reversibles)
• Si el cuerpo queda permanentemente deformado al dejar de aplicarle la fuerza se dice que el
cuerpo es inelástico o plástico. (Las deformaciones que se producen son irreversibles)
• El propósito es explicar el comportamiento elástico o deformativo de los cuerpos o estructuras
cuando están sometidas a cargas o fuerzas externas.
• La elasticidad pertenece a Resistencia de los Materiales, en donde al diseñar o construir, se
debe considerar el tipo de material y las dimensiones de ellas para obtener esfuerzos que
puedan soportarlos.

3. Elasticidad
Estudia las deformaciones de los cuerpos debido a las fuerzas que actúan sobre ellas. Las deformaciones de
los sólidos se explican en términos de los conceptos de esfuerzo y deformación.
Esfuerzo (σ).- Es la relación entre la fuerza o carga aplicada a un solido sobre un área o sección
transversal
Esfuerzo de tracción o tensión Esfuerzo de comprensión
Deformación (ε).- Se define como el cambio de forma de un cuerpo. El resultado de un esfuerzo es
una deformación
∆𝑙
∆𝑙
𝜎 =
𝐹
𝐴
𝑁
𝑚2
= 𝑃𝑎

4. TIPOS DE DEFORMACIONES
a) Deformación longitudinal o unitaria (𝜀𝑙).- Es el cociente entre la deformación y su
dimensión inicial. Curva esfuerzo-Deformación
Ley de Hooke.-En la zona elástica lineal “El esfuerzo y la
deformación unitaria son directamente proporcional”.
𝜎 𝑁 =
𝐹 𝑁
𝐴
𝜀𝑙 =
∆𝑙
𝑙0
∆𝑙
𝐹 𝑁
𝐴
= 𝐸
∆𝐿
𝐿0
𝜎 𝑁 = 𝐸 𝜀 𝐿
𝐸: 𝑀𝑜𝑑𝑢𝑙𝑜 𝑑𝑒 𝑌𝑜𝑢𝑛𝑔

5. b) Deformación unitaria por cizalladura o corte (𝜀 𝑐).-. Esta deformación se produce cuando se
aplican fuerzas opuestas a las dos caras contrarias del cuerpo, traduciéndose un desplazamiento de
planos paralelos en la dirección de la fuerza
De la Ley de Hooke
𝛷
Esfuerzo de corte
Ft/A
Deformación
de corte
∆X/L0
𝑇𝑔𝛷 =
∆𝑥
𝐿
𝜎𝑐 =
𝐹𝑡
𝐴
𝜎𝑐 = 𝑛 𝜀 𝑐
𝐹𝑡
𝐴
= 𝑛
∆𝑥
𝐿 𝑛: 𝑀𝑜𝑑𝑢𝑙𝑜 𝑑𝑒 Rigidez
𝜀 𝑐 =
∆𝑥
𝐿

6. c) Deformación unitaria volumétrica (𝜀 𝑣).- Esta deformación se produce cuando se aplican fuerzas
perpendiculares sobre toda la superficie del objeto (ejemplo, cuando un objeto es sumergido en un
líquido, cuando se infla un globo), produciendo variación de presión, la que producirá cambios de
volumen.
De la Ley de Hooke
Para: Compresión, ΔV es negativo
Tracción, ΔV es positivo
𝜎 𝑉 = 𝐵𝜀 𝑉
k=
1
𝐵
𝐶𝑜𝑒𝑓𝑖𝑐𝑖𝑒𝑛𝑡𝑒 𝑑𝑒 𝑐𝑜𝑚𝑝𝑟𝑒𝑛𝑠𝑖𝑏𝑖𝑙𝑖𝑑𝑎𝑑
𝐹 ⊥ 𝐴
𝜎𝑣 =
∆𝐹
𝐴
= ∆𝑃
𝜀 𝑣 =
∆𝑉
𝑉0
∆𝑃 = 𝛽
∆𝑉
𝑉0 𝛽: Modulo de comprensibilidad

7. d) Deformación lateral.- Cuando un cuerpo se estira, lateralmente sufre una contracción y viceversa,
para medirla se usa el coeficiente de Poisson (µ).Para un cilindro de 𝑟0 𝑦 𝐿0, las variaciones de sus
dimensiones son ∆𝑟 𝑦 ∆𝑙
𝜇 =
∆ 𝑟
𝑟0
∆ 𝐿
𝐿0
𝜂 =
𝐸
2 1 + 𝜇 𝐵 =
𝐸
3 1 − 2𝜇
0,25 < 𝜇 < 0,5
𝑃𝑎𝑟𝑎 𝑐𝑢𝑒𝑟𝑝𝑜𝑠 𝑝𝑜𝑟𝑜𝑠𝑜𝑠 𝜇 = 0
𝜇 =
𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑐𝑖𝑜𝑛 𝑙𝑎𝑡𝑒𝑟𝑎𝑙 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑎
𝐴𝑙𝑎𝑟𝑔𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑜
𝜎 𝑁 = 𝐸 𝜀 𝐿
𝑅𝑒𝑙𝑎𝑐𝑖𝑜𝑛 𝑒𝑛𝑡𝑟𝑒 𝑙𝑜𝑠 𝑚𝑜𝑑𝑢𝑙𝑜𝑠 𝑒𝑙𝑎𝑠𝑡𝑖𝑐𝑜𝑠
Para un solido de lado 𝐿 𝑥, 𝐿 𝑦, 𝐿 𝑧 𝑠𝑜𝑏𝑟𝑒 𝑒𝑙 𝑐𝑢𝑎𝑙 𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 𝑙𝑜𝑠 𝑒𝑠𝑓𝑢𝑒𝑟𝑧𝑜𝑠 𝜎 𝑥, 𝜎 𝑦, 𝜎𝑧;
𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 𝑎𝑙𝑎𝑟𝑔𝑎𝑚𝑒𝑖𝑛𝑡𝑜𝑠 + y contracciones (−)
∆𝑥 =
𝜎𝑥
𝐸
− 𝜇
𝜎 𝑦
𝐸
− 𝜇
𝜎𝑧
𝐸
=
𝜎𝑥 − 𝜇 𝜎 𝑦 − 𝜎𝑧
𝐸
∆z =
𝜎𝑧
𝐸
− 𝜇
𝜎𝑥
𝐸
− 𝜇
𝜎 𝑦
𝐸
=
𝜎𝑧 − 𝜇 𝜎𝑥 − 𝜎 𝑦
𝐸
∆y =
𝜎 𝑦
𝐸
− 𝜇
𝜎𝑥
𝐸
− 𝜇
𝜎𝑧
𝐸
=
𝜎 𝑦 − 𝜇 𝜎𝑥 − 𝜎𝑧
𝐸
∆𝐿

8. Modulo de elasticidad de materiales
Material Modulo de elasticidad
E(N/m2) 𝑛 (N/m2) B (N/m2)
Aluminio 7,0 x 1010 2,5 x 1010 7,5 x 1010
Cobre 11,0 x 1010 4,3 x 1010 14,0 x 1010
Hierro 19,0 x 1010 7,7 x 1010 16,0 x 1010
Plomo 1,7 x 1010 0,6 x 1010 4,1 x 1010
Nickel 20,6 x 1010 7,4 x 1010 17,0 x 1010
Laton 9,0 x 1010 3,5 x 1010 6,0 x 1010
Acero 20,0 x 1010 7,5 x 1010 16,0 x 1010
Vidrio óptico 6,0 x 1010 2,5 x 1010 5,0 x 1010
Hormigón 2,3 x 1010 - -
Agua - - 0,21 x 1010
Mercurio - - 2,8 x 1010

9. ENERGIA ELASTICA ACUMULADA EN UNA BARRA.- Una barra deformada elásticamente
almacena energía, numéricamente igual al trabajo hecho para tal deformación.
Este trabajo no se pierde, se almacena como energía
𝐹
𝐴
= 𝐸
∆𝐿
𝐿0
𝐹∆𝐿 = 𝐴𝐸
∆ 𝐿
𝐿0
U=
1
2
𝐴𝐸
𝐿0
∆𝐿2
=
1
2
𝐸𝑉0 𝜀 𝐿
2
𝑈 =
0
∆𝐿
𝐹∆𝐿 ∆𝐿 =
0
∆𝐿
𝐴𝐸
∆𝐿
𝐿0
𝑑∆𝐿 =
𝐴𝐸
𝐿0 0
∆𝐿
∆𝐿𝑑∆𝐿 =
1
2
𝐴𝐸
𝐿0
∆𝐿2
, donde K =
𝐴𝐸
𝐿0
∆𝑙
𝑑𝑈 = 𝐹∆𝐿 𝑑∆𝐿
𝑃𝑎𝑟𝑎 𝑢𝑛 𝑟𝑒𝑠𝑜𝑟𝑡𝑒: U=
1
2
𝐾∆𝐿2
𝐶𝑜𝑚𝑜 ∶ 𝜀 𝐿 =
∆𝐿
𝐿0

10. ESTRUCTURAS.- Es todo elemento capaz de soportar esfuerzos, las
estructuras constituyen el esqueleto de los mecanismos, edificios, puentes, etc.
Estructuras masivas
Estructuras trianguladas
Estructuras entramadas
Estructuras colgadas

11. MATERIALES Y ESTRUCTURAS
• Se pueden elaborar estructuras con muchos materiales, pero los más
usados a lo largo de la historia son:
Rascacielos, puentes, grandes
estructuras con vigas y pilares
Acero y hormigónActualidad
Puentes, estaciones de ferrocarril,
naves industriales
AceroRevolución
Industrial
Iglesias y palaciosPiedra, madera y ladrillosEdad Media (Gótico)
Iglesias y fortalezasPiedra, madera y ladrillosEdad Media
(Románico)
Teatros, acueductos, arcos,
bóvedas y cúpulas
Piedra, madera, ladrillo y
argamasa
Roma
Templos y pirámidesPiedra, madera y argamasaEgipto
CabañasMaderas y piedrasPrehistoria
ESTRUCTURASMATERIALESÉPOCA

13. Máquina hidráulica Baldwin para pruebas de Tension & Compresion

14. d) Deformación lateral.- Cuando un cuerpo se estira, lateralmente sufre una contracción y viceversa, para
medirla se usa el coeficiente de Poisson (µ).Para un cilindro de 𝑟0 𝑦 𝐿0, las variaciones de sus dimensiones son
∆𝑟 𝑦 ∆𝑙
𝜇 =
∆ 𝑟
𝑟0
∆ 𝐿
𝐿0
𝜂 =
𝐸
2 1 + 𝜇
𝐵 =
𝐸
3 1 − 2𝜇
0,25 < 𝜇 < 0,5
𝑃𝑎𝑟𝑎 𝑐𝑢𝑒𝑟𝑝𝑜𝑠 𝑝𝑜𝑟𝑜𝑠𝑜𝑠 𝜇 = 0
𝜇 =
𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑐𝑖𝑜𝑛 𝑙𝑎𝑡𝑒𝑟𝑎𝑙 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑎
𝐴𝑙𝑎𝑟𝑔𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑜
𝜎 𝑁 = 𝐸 𝜀 𝐿
∆′
𝑥=
𝜎𝑥
𝐸
𝜇 = −
∆′′
𝑦
∆′
𝑥
∆′′′
𝑧= −𝜇∆′
𝑦= −𝜇
𝜎 𝑦
𝐸
𝑅𝑒𝑙𝑎𝑐𝑖𝑜𝑛 𝑒𝑛𝑡𝑟𝑒 𝑙𝑜𝑠 𝑚𝑜𝑑𝑢𝑙𝑜𝑠 𝑒𝑙𝑎𝑠𝑡𝑖𝑐𝑜𝑠
Para un solido de lado 𝐿 𝑥, 𝐿 𝑦, 𝐿 𝑧 𝑠𝑜𝑏𝑟𝑒 𝑒𝑙 𝑐𝑢𝑎𝑙 𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 𝑙𝑜𝑠 𝑒𝑠𝑓𝑢𝑒𝑟𝑧𝑜𝑠 𝜎 𝑥, 𝜎 𝑦, 𝜎𝑧;
𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 𝑎𝑙𝑎𝑟𝑔𝑎𝑚𝑒𝑖𝑛𝑡𝑜𝑠 + y contracciones (−)
𝜇 = −
∆′′
𝑧
∆′
𝑥
∆′′
𝑧= −𝜇∆′
𝑥= −𝜇
𝜎𝑥
𝐸
∆′
𝑧=
𝜎𝑧
𝐸
𝜇 = −
∆′′
𝑥
∆′
𝑦
∆′′
𝑦= −𝜇∆′
𝑥= −𝜇
𝜎𝑥
𝐸
𝜇 = −
∆′′′
𝑧
∆′
𝑦
∆′′
𝑥= −𝜇∆′
𝑦= −𝜇
𝜎 𝑦
𝐸
∆′
𝑦=
𝜎 𝑦
𝐸
𝜇 = −
∆′′′
𝑥
∆′
𝑧
∆′′
′ 𝑥 = −𝜇∆′
𝑧= −𝜇
𝜎𝑧
𝐸
𝜇 = −
∆′′′
𝑦
∆′
𝑧
∆′′′
𝑦= −𝜇∆′
𝑧= −𝜇
𝜎𝑧
𝐸
∆𝑥 = ∆′
𝑥 + ∆′′
𝑥 + ∆′′′
𝑥=
𝜎𝑥
𝐸
− 𝜇
𝜎 𝑦
𝐸
− 𝜇
𝜎𝑧
𝐸
=
𝜎𝑥 − 𝜇 𝜎 𝑦 − 𝜎𝑧
𝐸
𝑅𝑒𝑠𝑢𝑚𝑖𝑒𝑛𝑑𝑜:
∆z = ∆′
𝑧 + ∆′′
𝑧 + ∆′′′
𝑧=
𝜎𝑧
𝐸
− 𝜇
𝜎𝑥
𝐸
− 𝜇
𝜎 𝑦
𝐸
=
𝜎𝑧 − 𝜇 𝜎𝑥 − 𝜎 𝑦
𝐸
∆y = ∆′
𝑦 + ∆′′
𝑦 + ∆′′′
𝑦=
𝜎 𝑦
𝐸
− 𝜇
𝜎𝑥
𝐸
− 𝜇
𝜎𝑧
𝐸
=
𝜎 𝑦 − 𝜇 𝜎𝑥 − 𝜎𝑧
𝐸
∆𝐿