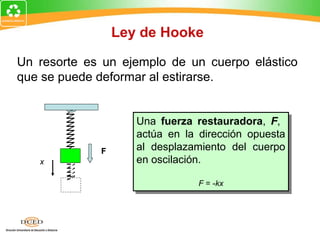
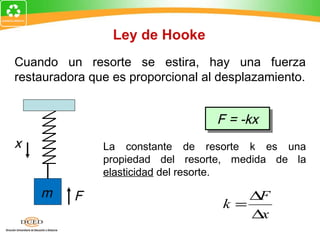
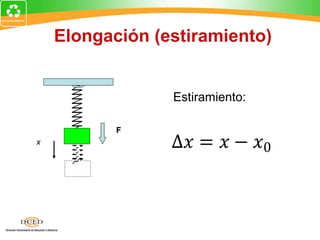
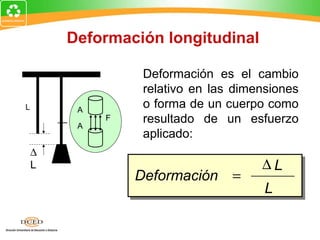
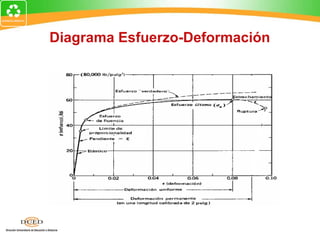
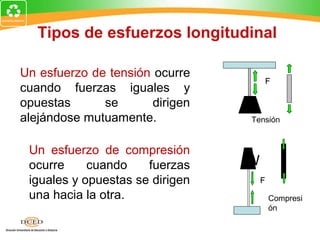
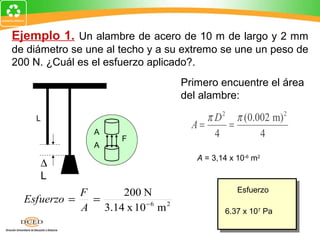
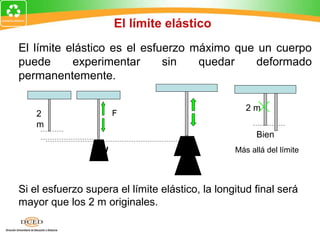
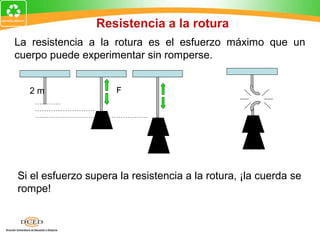
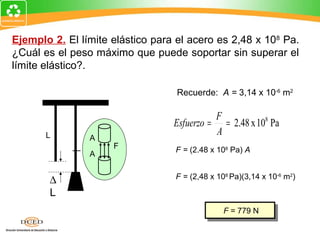
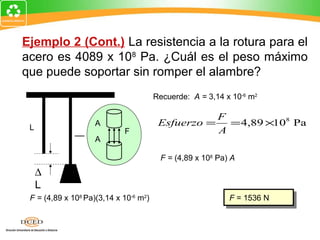
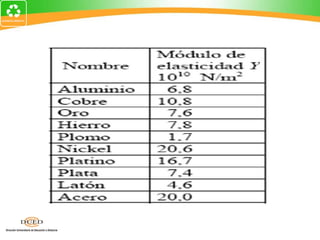
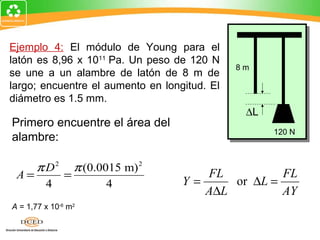
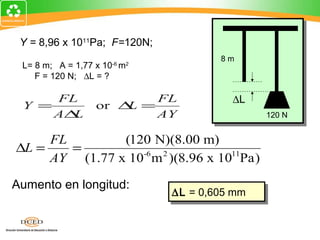
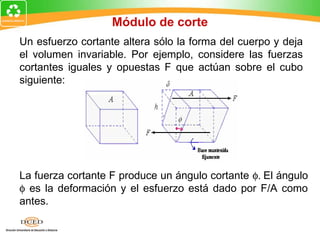
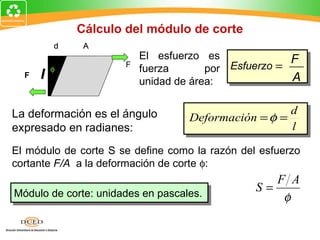
Este documento presenta una introducción al tema de la elasticidad en Física II. Explica conceptos clave como elasticidad, deformación elástica y plástica, diagrama de esfuerzo-deformación, ley de Hooke, esfuerzo cortante, deformación volumétrica y módulos de elasticidad como el módulo de Young y el módulo de corte. Incluye ejemplos para ilustrar cómo calcular esfuerzos, deformaciones, límites elásticos y módulos de elasticidad para diferentes materiales.

1. CICLO 2013-I Módulo:I
Unidad: I Semana: 1
FISICA II
Lic. Fis. Carlos Lévano Huamaccto

2. ELASTICIDAD

3. CONTENIDOS TEMÁTICOS
• Introducción
• Elasticidad
• Relación entre los cuerpos elásticos y los inelásticos
• Diagrama de Esfuerzo o Deformación. Deformación
elástica y plástica . Esfuerzo deformación Unitaria.
• Ley de Hooke
• Deformación Cortante o de Cizalladura
• Deformación Volumétrica.

4. ORIENTACIONES
Hasta ahora en nuestro estudio de mecánica hemos asumido que
los cuerpos son indeformables; esto no es cierto, aunque se
justifica cuando los efectos de la deformaciones carecen de
importancia.
En este capítulo trataremos sobre los cambios de forma producidos
en un cuerpo cuando está bajo la acción de una fuerza, esto es,
en el sentido del comportamiento de los materiales bajo la acción
de diversos esfuerzos, iniciándonos en la técnica del diseño.

5. ELASTICIDAD
Estudia las deformaciones que experimentan los
cuerpos y los procesos relacionados con el cuerpo
bajo la acción de fuerzas externas.

6. Propiedades de elásticidad
Un elásticidad es aquel que regresa a su forma original después de una
Un elásticidad es aquel que regresa a su forma original después de una
deformación , , una vez que cesa la fuerza que esta originando la de
deformación una vez que cesa la fuerza que esta originando la de
formación.
formación.

7. Ley de Hooke
Un resorte es un ejemplo de un cuerpo elástico
que se puede deformar al estirarse.
Una fuerza restauradora, F,
Una fuerza restauradora, F,
actúa en la dirección opuesta
actúa en la dirección opuesta
F al desplazamiento del cuerpo
al desplazamiento del cuerpo
x en oscilación.
en oscilación.
F = -kx
F = -kx

8. Ley de Hooke
Cuando un resorte se estira, hay una fuerza
restauradora que es proporcional al desplazamiento.
F = -kx
F = -kx
x La constante de resorte k es una
propiedad del resorte, medida de la
elasticidad del resorte.
m F ∆F
k=
∆x

9. Elongación (estiramiento)
Estiramiento:
F
x

10. Esfuerzo
Esfuerzo es la razón de una fuerza aplicada F al área
A sobre la que actúa:
F
Esfuerzo = N lb
Unidades : Pa = 2 o
A m in 2
Ejemplos: Cambio en longitud por unidad de longitud;
Ejemplos: Cambio en longitud por unidad de longitud;
cambio en volumen por unidad de volumen.
cambio en volumen por unidad de volumen.

11. Deformación longitudinal
Deformación es el cambio
relativo en las dimensiones
L A
o forma de un cuerpo como
A
F resultado de un esfuerzo
aplicado:
∆
L ∆L
Deformación =
L

12. Diagrama Esfuerzo-Deformación

13. Tipos de esfuerzos longitudinal
Un esfuerzo de tensión ocurre
F
cuando fuerzas iguales y
opuestas se dirigen
W
alejándose mutuamente. Tensión
Un esfuerzo de compresión
ocurre cuando fuerzas W
iguales y opuestas se dirigen F
una hacia la otra. Compresi
ón

14. Ejemplo 1. Un alambre de acero de 10 m de largo y 2 mm
de diámetro se une al techo y a su extremo se une un peso de
200 N. ¿Cuál es el esfuerzo aplicado?.
Primero encuentre el área
del alambre:
L π D 2 π (0.002 m) 2
A= =
A
F
4 4
A
A = 3,14 x 10-6 m2
∆
L
F 200 N Esfuerzo
Esfuerzo = =
A 3.14 x 10 − 6 m 2 6.37 x 107 Pa

15. Ejemplo 1 (Cont.) Un alambre de acero de 10
m se estira 3.08 mm debido a la carga de 200
N. ¿Cuál es la deformación longitudinal?
Dado: L = 10 m; ∆L = 3.08 mm
∆L 0.00308 m
L Deformación = =
L 10 m
Deformación longitudinal
∆
L 3.08 x 10-4

16. El límite elástico
El límite elástico es el esfuerzo máximo que un cuerpo
puede experimentar sin quedar deformado
permanentemente.
2m
2 F
m
Bien
W W Más allá del límite
W
Si el esfuerzo supera el límite elástico, la longitud final será
mayor que los 2 m originales.

17. Resistencia a la rotura
La resistencia a la rotura es el esfuerzo máximo que un
cuerpo puede experimentar sin romperse.
2m F
W W W
W W
Si el esfuerzo supera la resistencia a la rotura, ¡la cuerda se
rompe!

18. Ejemplo 2. El límite elástico para el acero es 2,48 x 108 Pa.
¿Cuál es el peso máximo que puede soportar sin superar el
límite elástico?.
Recuerde: A = 3,14 x 10-6 m2
F
Esfuerzo = = 2.48 x 108 Pa
L A
A
F F = (2.48 x 108 Pa) A
A
F = (2,48 x 108 Pa)(3,14 x 10-6 m2)
∆
L
F = 779 N
F = 779 N

19. Ejemplo 2 (Cont.) La resistencia a la rotura para el
acero es 4089 x 108 Pa. ¿Cuál es el peso máximo
que puede soportar sin romper el alambre?
Recuerde: A = 3,14 x 10-6 m2
F
L
A Esfuerzo = = 4,89 ×108 Pa
F A
A
F = (4,89 x 108 Pa) A
∆
L
F = (4,89 x 108 Pa)(3,14 x 10-6 m2) F = 1536 N
F = 1536 N

20. El módulo de elasticidad
Siempre que el límite elástico no se supere, una
deformación elástica (deformación) es directamente
proporcional a la magnitud de la fuerza aplicada por
unidad de área (esfuerzo).
esfuerzo
Módulo de elasticidad =
deformación

21. Clases de módulos de elasticidad

22. Ejemplo 3. En el ejemplo anterior, el esfuerzo aplicado al
alambre de acero fue 6.37 x 107 Pa y la deformación fue 3.08
x 10-4. Encuentre el módulo de elasticidad para el acero.
esfuerzo 6.37 × 107 Pa
Módulo = =
L
deformación 3.08 × 10 − 4
Módulo = 207 xx1099Pa
Módulo = 207 10 Pa
∆
L
Este módulo de elasticidad longitudinal se llama módulo de Young yy se
Este módulo de elasticidad longitudinal se llama módulo de Young se
denota con el símbolo Y.
denota con el símbolo Y.

23. Módulo de Young
Para materiales cuya longitud es mucho mayor que el
ancho o espesor, se tiene preocupación por el módulo
longitudinal de elasticidad, o módulo de Young (Y).
esfuerzo longitudinal
Módulo de Young =
deformación longitudinal
Y=
F/A
=
FL Unidades: Pa , lb
∆L / L A ∆L 2
in.

25. Ejemplo 4: El módulo de Young para el
latón es 8,96 x 1011 Pa. Un peso de 120 N
8m
se une a un alambre de latón de 8 m de
largo; encuentre el aumento en longitud. El
diámetro es 1.5 mm.
∆L
Primero encuentre el área del
120 N
alambre:
π D 2 π (0.0015 m) 2
A= = FL FL
4 4 Y= or ∆L =
A∆L AY
A = 1,77 x 10-6 m2

26. Y = 8,96 x 1011Pa; F=120N;
8m
L= 8 m; A = 1,77 x 10 m
-6 2
F = 120 N; ∆L = ?
FL FL ∆L
Y = or ∆ =
L
A∆L AY 120 N
FL (120 N)(8.00 m)
∆L = = -6 2 11
AY (1.77 x 10 m )(8.96 x 10 Pa)
Aumento en longitud:
∆L = 0,605 mm
∆L = 0,605 mm

27. Módulo de corte
Un esfuerzo cortante altera sólo la forma del cuerpo y deja
el volumen invariable. Por ejemplo, considere las fuerzas
cortantes iguales y opuestas F que actúan sobre el cubo
siguiente:
La fuerza cortante F produce un ángulo cortante φ. El ángulo
φ es la deformación y el esfuerzo está dado por F/A como
antes.

28. Cálculo del módulo de corte
d A
El esfuerzo es F
φ
F
fuerza por Esfuerzo =
F l unidad de área: A
La deformación es el ángulo d
Deformación = φ =
expresado en radianes: l
El módulo de corte S se define como la razón del esfuerzo
cortante F/A a la deformación de corte φ:
F A
Módulo de corte: unidades en pascales.
S=
Módulo de corte: unidades en pascales. φ

30. Ejemplo 5. Un perno de acero (S = 8,27 x 1010 Pa) de 1 cm
de diámetro se proyecta 4 cm desde la pared. Al extremo se
aplica una fuerza cortante de 36000 N. ¿Cuál es la
desviación d del perno?
π D 2 π (0.01 m) 2
A= =
l 4 4
d Área: A = 7,85 x 10-5 m2
F F A F A Fl Fl
S= = = ; d=
φ d l Ad AS
(36, 000 N)(0.04 m)
d= d = 0.222 mm
d = 0.222 mm
(7.85 x 10-5 m 2 )(8.27 x 1010 Pa)

31. Modulo Volumétrica
No todas las deformaciones son lineales. A veces un
esfuerzo aplicado F/A resulta en una disminución del
volumen. En tales casos, existe un módulo volumétrico B de
elasticidad.
El módulo volumétrico es negativo debido a la disminución en V.
El módulo volumétrico es negativo debido a la disminución en V.

32. El Módulo Volumétrico
esfuerzo volumétrico −F A
B= =
deformación volumétrica ∆V V
Dado que F/A por lo general es la presión P, se puede
escribir:
−P − PV
B= =
∆V / V ∆V
Las unidades siguen siendo pascales (Pa) pues la
deformación es adimensional.

33. Ejemplo7.- Una prensa hidrostática contiene 5
litros de aceite. Encuentre la disminución en
volumen del aceite si se sujeta a una presión de
3000 kPa. (Suponga que B = 1700 MPa.)
−P − PV −PV −(3 x 106 Pa)(5 L)
B= = ∆V = =
∆V / V ∆V B (1.70 x 109 Pa)
∆V = -8.82 mL
∆V = -8.82 mL
Disminución en V,

35. GRACIAS