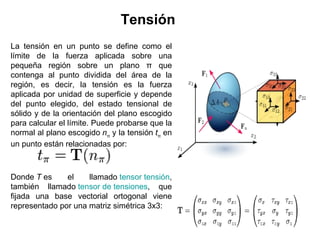
Este documento trata sobre la elasticidad en mecánica clásica. Explica que la elasticidad es la propiedad de los objetos de cambiar de forma bajo una fuerza y recuperar su forma original cuando la fuerza cesa. Presenta la Ley de Hooke, la cual establece que la deformación es directamente proporcional a la fuerza aplicada. También cubre conceptos como límites de elasticidad, elasticidad lineal, tensor tensión y tensor deformación.

1. MECÁNICA CLÁSICA
ELASTICIDAD
Fernando Daniel Rojas
Christian Ruiz
Sergio Luis Arroyo

3. DEFORMACIÓN DE LAS FUERZAS
• La deformación de un cuerpo es uno de los dos
efectos que puede producir una fuerza.
• Los cuerpos se clasifican en:
Elásticos:
Si recuperan su forma anterior.
Plásticos:
Si la deformación permanece

4. Elasticidad
Propiedad de cambiar de
forma cuando actúa una
fuerza de deformación sobre
un objeto, y el objeto regresa
a su forma original cuando
cesa la deformación.

5. Límites de Elasticidad
Si se estira o se comprime más allá de
cierta cantidad, ya no regresa a su
estado original, y permanece deformado.

6. Ley de Hooke
“La cantidad de estiramiento
o de compresión (cambio de
longitud), es directamente
proporcional a la fuerza
aplicada.”

7. Ley de Hooke
Se puede expresar matemáticamente así:
• K es la constante de proporcionalidad o de elasticidad.
• es la deformación
• El signo ( - ) en la ecuación se debe a la fuerza
restauradora que tiene sentido contrario al desplazamiento.
• Las unidades son: Newton/metro (New/m) – Libras/pies (Lb/
p).

8. Elasticidad (mecánica de sólidos)
En física e ingeniería, el
término elasticidad design
a la propiedad mecánica
de ciertos materiales de
sufrir deformaciones
reversibles cuando se
encuentran sujetos a la
acción de fuerzas
exteriores y de recuperar
la forma original si estas
fuerzas exteriores se
eliminan.

9. Elasticidad lineal
Un caso particular de sólido elástico se presenta cuando las
tensiones y las deformaciones están relacionadas linealmente,
mediante la siguiente ecuación constitutiva:
Cuando eso sucede decimos que tenemos un sólido elástico lineal.
La teoría de la elasticidad lineal es el estudio de sólidos elásticos
lineales sometidos a pequeñas deformaciones de tal manera que
además los desplazamientos y deformaciones sean "lineales", es
decir, que las componentes del campo de desplazamientos u sean
muy aproximadamente una combinación lineal de las componentes
del tensor deformación del sólido. En general un sólido elástico lineal
sometido a grandes desplazamientos no cumplirá esta condición. Por
tanto la teoría de la elasticidad lineal sólo es aplicable a:

10. • Sólidos elásticos lineales, en los que tensiones y
deformaciones estén relacionadas linealmente (linealidad
material).
• Deformaciones pequeñas, es el caso en que deformaciones
y desplazamientos están relacionados linealmente. En este
caso puede usarse el
tensor deformación lineal de Green-Lagrange para
representar el estado de deformación de un sólido (linealidad
geométrica).
Debido a los pequeños desplazamientos y deformaciones a los
que son sometidos los cuerpos, se usan las siguientes
simplificaciones y aproximaciones para sistemas estables:
• Las tensiones se relacionan con las superficies no
deformadas
• Las condiciones de equilibrio se presentan para el sistema no
deformado
• Para determinar la estabilidad de un sistema hay presentar
las condiciones de equilibrio para el sistema deformado.

11. Tensión
La tensión en un punto se define como el
límite de la fuerza aplicada sobre una
pequeña región sobre un plano π que
contenga al punto dividida del área de la
región, es decir, la tensión es la fuerza
aplicada por unidad de superficie y depende
del punto elegido, del estado tensional de
sólido y de la orientación del plano escogido
para calcular el límite. Puede probarse que la
normal al plano escogido nπ y la tensión tπ en
un punto están relacionadas por:
Donde T es el llamado tensor tensión,
también llamado tensor de tensiones, que
fijada una base vectorial ortogonal viene
representado por una matriz simétrica 3x3:

12. Deformación
En teoría lineal de la elasticidad dada la pequeñez de las deformaciones es una
condición necesaria para poder asegurar que existe una relación lineal entre los
desplazamientos y la deformación. Bajo esas condiciones la deformación puede
representarse adecuadamente mediante el tensor deformación infinitesimal que
viene dada por:
Los componentes de la diagonal principal contienen los alargamientos
(dilataciones), mientras que el resto de los componentes del tensor son los medios
desplazamientos.
Las componentes están linealmente relacionadas con los desplazamientos
mediante esta relación:

13. Ley de elasticidad de Hooke

14. MUCHAS GRACIAS