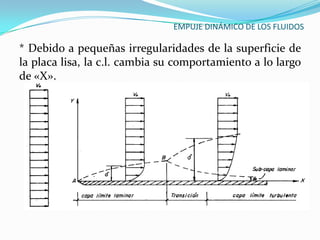
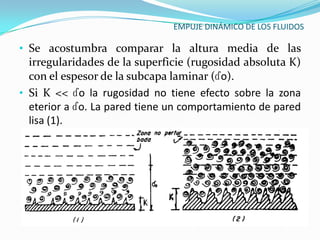
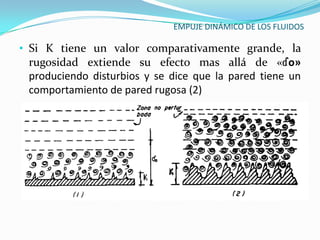
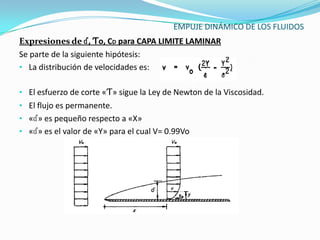
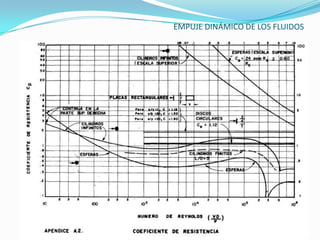
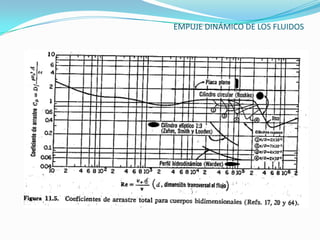
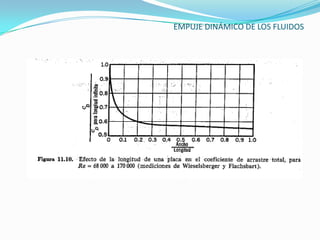
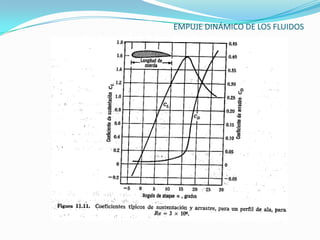
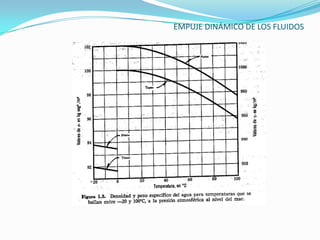
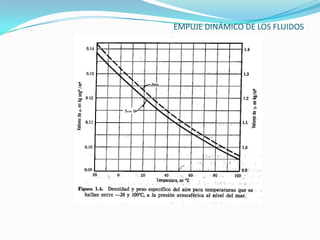
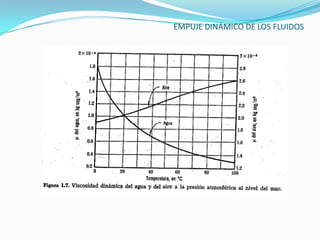
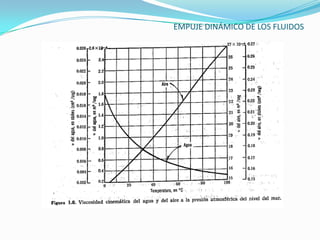
El documento describe la teoría del empuje dinámico de los fluidos sobre cuerpos. Explica la capa límite, donde ocurren las fuerzas de fricción, y cómo esta varía entre laminar y turbulento dependiendo del número de Reynolds. También presenta expresiones matemáticas para calcular el espesor y fuerzas de la capa límite laminar y turbulento, así como el arrastre y sustentación que un fluido ejerce sobre un cuerpo.

2. EMPUJE DINÁMICO DE LOS FLUIDOS
• Los fluidos en movimiento ejercen fuerzas sobre los
cuerpos que estan de por medio.
• La ecuación de la cantidad de movimiento permite en
muchos casos evaluar estas fuerzas.
• La teoría de la CAPA LIMITE (c.l.) proporciona las
bases para un análisis más minucioso y exacto
completando con coeficientes que se determinan
experimentalmente.
• Para el ingeniero civil el interés se centra en poder
averiguar el empuje dinámico del aire sobre
estructuras como
chimeneas,torres, edificios, puentes, etc. Y empuje
dinámico del agua sobre pilares, rejillas, compuertas.

3. EMPUJE DINÁMICO DE LOS FLUIDOS
TEORIA DE LA CAPA LIMITE
• Se considera un flujo plano, irrotacional, de velocidad
uniforme.
• Se denomina Capa Limite a esta región muy proxima a
la superficie de la placa, en que se manifiestan efectos
viscosos resistentes.
• Todas las perdidas de carga por fricción tiene lugar
dentro de la c.l. y el flujo exterior a ella puede
considerarse como flujo potencial carente de
viscosidad.

4. EMPUJE DINÁMICO DE LOS FLUIDOS
TEORIA DE LA CAPA LIMITE
• La velocidad del fluido en el punto de contacto con la
placa vale cero.
• La gradiente (dv/dy) y el esfuerzo de corte (Ƭo) es
máximo en la frontera o en la pared.

5. EMPUJE DINÁMICO DE LOS FLUIDOS
* Fuera de la c.l. el efecto viscoso vale cero, así como la
gradiente y el esfuerzo de corte valen cero. Y se
restablece el flujo potencial, irrotacional, de velocidad
uniforme Vo

6. EMPUJE DINÁMICO DE LOS FLUIDOS
* Debido a pequeñas irregularidades de la superficie de
la placa lisa, la c.l. cambia su comportamiento a lo largo
de «X».

7. EMPUJE DINÁMICO DE LOS FLUIDOS
• El diagrama de la c.l. es asintotico al valor de Vo, por lo
que conviene definir como espesor c.l. (ɗ) la distancia
Y. a la cual V=0.99 Vo
• La velocidad de la c.l. laminar y la sub capa laminar
varía según una parábola, y en la c.l. turbulenta según
una ley logaritmica.

8. EMPUJE DINÁMICO DE LOS FLUIDOS
• Para números de Reynolds bajos toda c.l. resulta
laminar. (1).
• Para número de Reynolds intermedios la c.l. es
turbulenta, pero subsiste una subcapa laminar (2).
• Para número de Reynolds grandes la c.l. es totalmente
turbulento.

9. EMPUJE DINÁMICO DE LOS FLUIDOS
• Se acostumbra comparar la altura media de las
irregularidades de la superficie (rugosidad absoluta K)
con el espesor de la subcapa laminar (ɗo).
• Si K << ɗo la rugosidad no tiene efecto sobre la zona
eterior a ɗo. La pared tiene un comportamiento de pared
lisa (1).

10. EMPUJE DINÁMICO DE LOS FLUIDOS
• Si K tiene un valor comparativamente grande, la
rugosidad extiende su efecto mas allá de «ɗo»
produciendo disturbios y se dice que la pared tiene un
comportamiento de pared rugosa (2)

11. EMPUJE DINÁMICO DE LOS FLUIDOS

12. EMPUJE DINÁMICO DE LOS FLUIDOS
Expresiones de ɗ, Ƭo, CD para CAPA LIMITE LAMINAR
Se parte de la siguiente hipótesis:
• La distribución de velocidades es:
• El esfuerzo de corte «Ƭ» sigue la Ley de Newton de la Viscosidad.
• El flujo es permanente.
• «ɗ» es pequeño respecto a «X»
• «ɗ» es el valor de «Y» para el cual V= 0.99Vo

13. EMPUJE DINÁMICO DE LOS FLUIDOS
Las ecuaciones para una capa límite laminar serán:
a) Ecuación de Blasius para (ɗ)
a) Expresión de (Ƭo), analítica y experimentalmente se
obtiene:
b) Expresión de (CD)

14. EMPUJE DINÁMICO DE LOS FLUIDOS
Expresiones de ɗ, Ƭo, CD para CAPA LIMITE TURBULENTO
Difieren de las dos primeras hipótesis:
• La distribución de velocidades sigue la ley de Prandtl de la potencia de 1/7
(por simplicidad en vez de la ley Logaritmica).
• El esfuerzo de corte sigue cierta ley de tal manera que en la placa vale:

15. EMPUJE DINÁMICO DE LOS FLUIDOS
Las ecuaciones para una capa limite turbulento serán:
a) Expresión de (ɗ)
b) Expresión de (Ƭo),
c) Expresión de (CD)

16. EMPUJE DINÁMICO DE LOS FLUIDOS
EMPUJE DINÁMICO: ARRASTRE Y SUSTENTACIÓN;
Es la resistencia o arrastre que un fluido en movimiento ejerce sobre un cuerpo
sumergido en dicho fluido, y es causado por dos factores.
a) El ESFUERZO CORTANTE que produce fuerzas tangenciales obre la
superficie del cuerpo en razón de la viscosidad, dentro de la capa limite.
b) Las INTENSIDADES DE PRESIÓN, al variar sobre la superficie del cuerpo
por efectos dinámicos.

17. EMPUJE DINÁMICO DE LOS FLUIDOS
ARRASTRE (D): Es la componente de esta fuerza resultante (Fr) en la dirección
de la velocidad general del flujo.
SUSTENTACION (L): Es la componente normal de la fuerza resultante Fr.

18. EMPUJE DINÁMICO DE LOS FLUIDOS

19. EMPUJE DINÁMICO DE LOS FLUIDOS

20. EMPUJE DINÁMICO DE LOS FLUIDOS

21. EMPUJE DINÁMICO DE LOS FLUIDOS

22. EMPUJE DINÁMICO DE LOS FLUIDOS

23. EMPUJE DINÁMICO DE LOS FLUIDOS

24. EMPUJE DINÁMICO DE LOS FLUIDOS

25. EMPUJE DINÁMICO DE LOS FLUIDOS

26. EMPUJE DINÁMICO DE LOS FLUIDOS