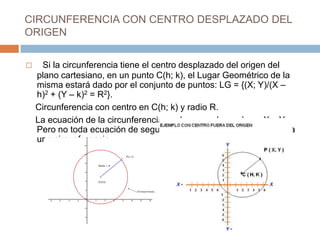
El documento describe las circunferencias en un plano cartesiano. Explica que una circunferencia es el conjunto de puntos equidistantes de un punto central llamado centro. Define la ecuación de una circunferencia con centro en el origen como X2 + Y2 = R2, donde R es el radio. También define la ecuación de una circunferencia con centro desplazado del origen como (X - h)2 + (Y - k)2 = R2, donde (h, k) son las coordenadas del centro.

1. CICUNFERENCIA EN
UN PLANO
CARTESIANO
Stephania Gil Martínez
Laura Alejandra Claros
Yachac Andrés Correa
Diego Alejandro Vargas
Carlos Corredor
1001

2. TRASLACION DE
EJES
 Los movimientos que se pueden hacer con los ejes
cartesianos son de dos tipos: traslaciones y rotaciones,
ya que estos movimientos no alteran las distancias entre
puntos, ni los ángulos entre rectas.
 Este proceso de cambiar de un par de ejes a otro se le
llama “transformaciones de coordenadas”.

3. CIRCUNFERENCIA
 Es el conjunto de todos los puntos sobre un plano “” que
son equidistantes de un punto fijo sobre el plano. Al
punto fijo se le llama centro y a la distancia de cualquier
punto de ella al centro se llama radio
Es decir:

4. CIRCUNFERENCIA CON CENTRO EN EL
ORIGEN
 La circunferencia con centro en origen del sistema
cartesiano y radio igual a R es el Lugar Geométrico de
todos los puntos que satisfacen la condición de que la
suma del cuadrado de la distancia a cada eje coordenado
es igual al cuadrado del radio:
LG = {(X; Y)/X2 + Y2 = R2} Circunferencia con
centro en el origen y radio = R.

5. CIRCUNFERENCIA CON CENTRO DESPLAZADO DEL
ORIGEN
 Si la circunferencia tiene el centro desplazado del origen del
plano cartesiano, en un punto C(h; k), el Lugar Geométrico de la
misma estará dado por el conjunto de puntos: LG = {(X; Y)/(X –
h)2 + (Y – k)2 = R2}.
Circunferencia con centro en C(h; k) y radio R.
La ecuación de la circunferencia es de segundo grado en X e Y.
Pero no toda ecuación de segundo grado en X e Y corresponde a
una circunferencia.