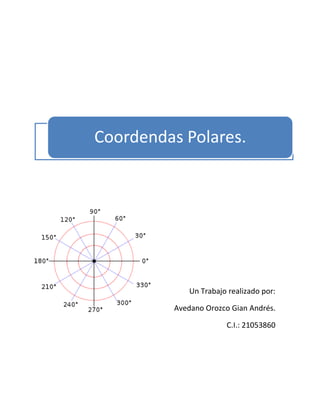
Las coordenadas polares son un sistema de coordenadas que representa cada punto en un plano mediante su distancia (r) al origen y el ángulo (θ) que forma con el eje x positivo. Permiten describir de forma simple curvas circulares y fenómenos relacionados con distancias y ángulos. Algunas aplicaciones incluyen modelar movimientos orbitales, navegación, y calcular límites y integrales donde la región de integración involucra circunferencias u otras curvas definidas por ecuaciones polares.

1. Coordendas Polares.
Un Trabajo realizado por:
Avedano Orozco Gian Andrés.
C.I.: 21053860

2. Cualquier uso que implica geometría circular o el Los usos de coordenadas polares son
movimiento radial se adapta ideal a los
coordenadas polares, porque estas geometrías se absolutamente variados. Los gráficos de la
pueden describir con ecuaciones relativamente coordenada polar se han utilizado para
simples en un sistema coordinado polar; sus modelar los campos de sonidos
gráficos son más curvilíneos o circular en el producidos variando localizaciones del
aspecto comparado a ésos en sistemas altavoz o las áreas donde diversos tipos
coordinados rectangulares. de micrófonos pueden la mejor coger el
Consecuentemente, las coordenadas polares
tienen uso el representar de los modelos de los sonido. Las coordenadas polares son de la
fenómenos del mundo real que tienen formas gran importancia que modela
semejantemente redondeadas. movimientos orbitales en astronomía y
viaje espacial.
Importancia
de las
Coordenadas
Polares.
Se expresan los coordenadas polares
como (r, θ). La letra r es la distancia del
origen al ángulo representado por la theta
griega de la letra, θ, donde r puede ser un Las coordenadas polares son una forma
número positivo o negativo. Si se utiliza de expresar la posición respecto a un
una distancia negativa, la magnitud de la plano de dos dimensiones.
distancia no cambia, pero la dirección se
toma enfrente del θ del ángulo en el otro
lado del origen.

3. Resumen Teorico.
Sistema de Coordenadas Polares:
A todo punto del plano cuyas coordenadas rectangulares
son podemos asignarle las siguientes coordenadas:
=distancia del origen de coordenadas al punto
=ángulo desde el semieje positivo del eje al segmento que une
el origen de coordenadas con
Representado gráficamente sería así:

4. Conversión de Coordenadas:
Para la conversión de coordenadas ya sean rectangulares o polares,
se usan diferentes fórmulas como las que veremos a continuación:
Polares en función a las Rectangulares:
Definido un punto en coordenadas polares por su ángulo
sobre el eje x, y su distancia r al centro de coordenadas, se
tiene:
1.
2.
Rectangulares en función de las Polares:
Definido un punto del plano por sus coordenadas rectangulares
(x,y), se tiene que la coordenada polar r es:
(Aplicando el Teorema de Pitágoras)
A.
B.

5. Para obtener θ en el intervalo *0, 2π), se deben usar las
siguientes fórmulas ( denota la inversa de la
función tangente):
Para obtener θ en el intervalo (−π, π+, se deben usar las
siguientes fórmulas:
Relación entres la Coordenadas Polares y
Rectangulares:

6. Ecuaciones en coordenadas polares:
Se le llama ecuación polar a la ecuación que define
una curva expresada en coordenadas polares. En muchos
casos se puede especificar tal ecuación definiendo como
una función de θ. La curva resultante consiste en una serie de
puntos en la forma ( (θ), θ) y se puede representar como
la gráfica de una función .
Debido a la naturaleza circular del sistema de coordenadas
polar, muchas curvas se pueden describir con una simple
ecuación polar, mientras que en su forma cartesiana sería
mucho más intrincado. Algunas de las curvas más conocidas
son:
La Rosa Polar:
Ej.: una rosa dentro de otra
Un caso interesante y especial que se puede dar es el que se
muestra en la gráfica que vemos a continuación, donde se aprecia
una rosa de tres pétalos precisamente dentro de otra rosa de tres
pétalos u hojas. Veamos:

7. La Cardioides:
Ej.: cardioide simétrica con respecto al eje polar y que apunta hacia
la derecha.
Podemos observar que se distingue una figura como de un
corazón, razón por la cual se llama este gráfico cardioide. La función
que lo ha generado es:
Circunferencia:
Ej.: la circunferencia, la cual será formada en el gráfico polar
mediante la siguiente función:

8. Espiral de Arquímedes:
Ej.: espiral conocida como espiral de Fermat, pues fue examinada
por Fermat en 1936. Su ecuación es r² = a² + . En el siguiente
ejemplo se muestra una función y su respectiva gráfica que nos
permiten conocer la espiral de Fertat:
Área de una región plana en Coordenadas Polares:
Área de la región encerrada por la gráfica de una función en
coordenadas polares: Sea r = r (θ) la ecuación de una curva en
coordenadas polares de forma que r (θ) sea una función continúa
en el intervalo *α, β+.

9. Aplicaciones:
Las coordenadas polares son enormemente interesantes al estudiar
fenómenos relacionados con distancias y ángulos (a grandes rasgos
se podría decir que interesan a la hora de estudiar conceptos
relacionados con elipses y circunferencias). Vamos a enumerar
unos cuantos:
 Cálculo de límites dobles: a la hora de calcular un límite doble
el método definitivo es el método del paso a coordenadas
polares. Se pasa con ellas a un límite dependiente de una
única variable, (en concreto ), utilizando las ecuaciones
de cambio de rectangulares a polares y se estudia si dicho
límite depende del ángulo . Si no existe tal dependencia el
límite inicial existe y su valor es el obtenido en el límite en
polares.
 Ecuaciones de curvas: las coordenadas polares simplifican la
expresión de las ecuaciones de ciertas curvas. Por ejemplo, la
circunferencia de centro y radio tiene a como
ecuación en coordenadas rectangulares y a como
ecuación en polares.
 Forma polar de un número complejo: todo punto del plano
con coordenadas rectangulares es la representación
gráfica del número complejo (esta forma de
representar un número complejo se denomina forma

10. binómica del ). Pasando a polares obtenemos el módulo ( ) y
el argumento ( ) de y con ello laforma polar de :
 Cálculo de integrales dobles: cuando la región de integración
de una integral doble es una circunferencia o una elipse (o
parte de alguna de ellas) pasar a coordenadas polares es una
opción muy interesante ya que simplifica mucho el cálculo de
los límites de integración de la misma.
 Navegación marítima: como la navegación marítima se basa
en ángulos y distancias la utilización de las coordenadas
polares simplifica mucho los cálculos necesarios para realizar
dicha actividad.
 Cálculos orbitales: las razones son las mismas que en el caso
anterior.