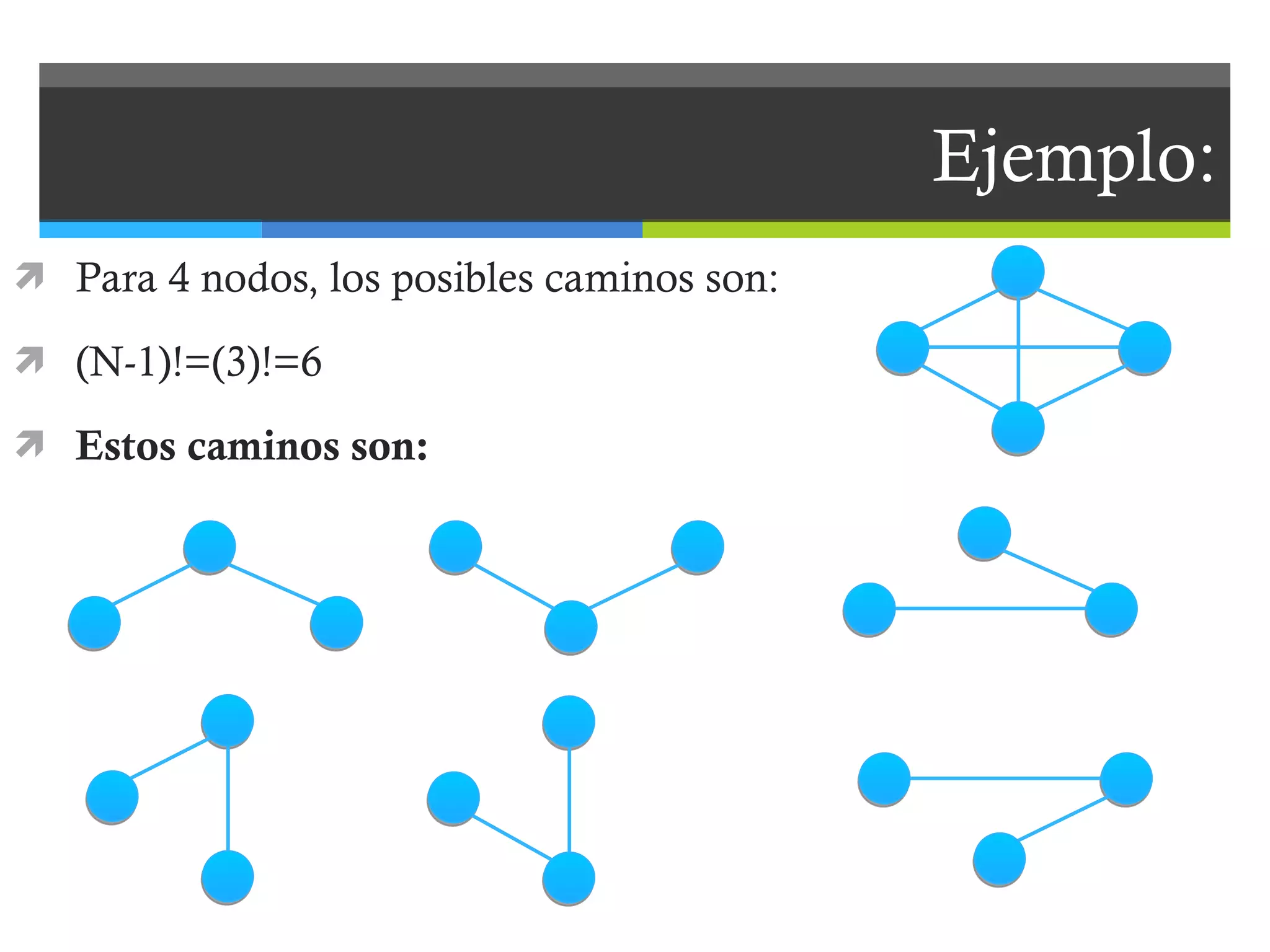
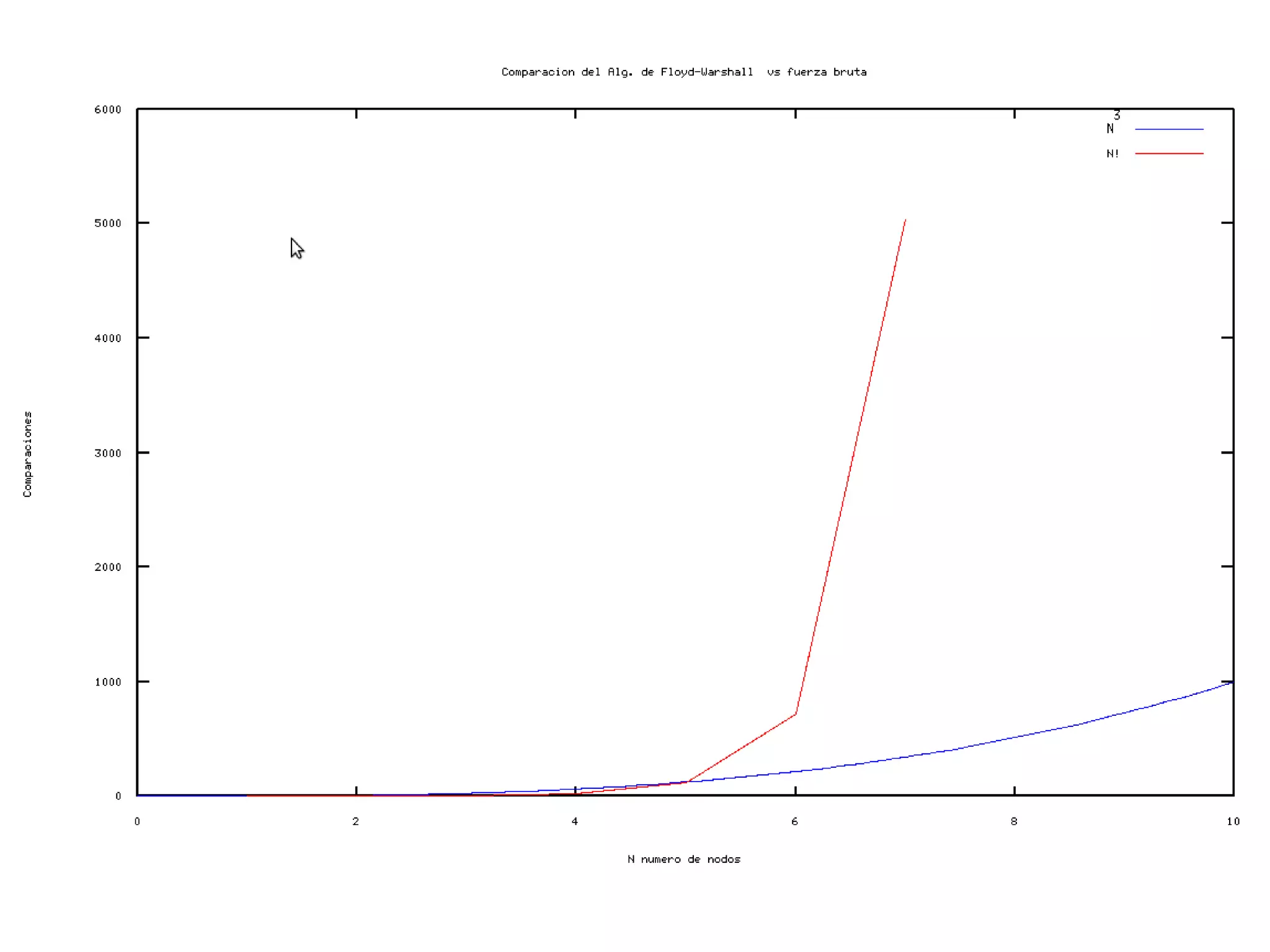
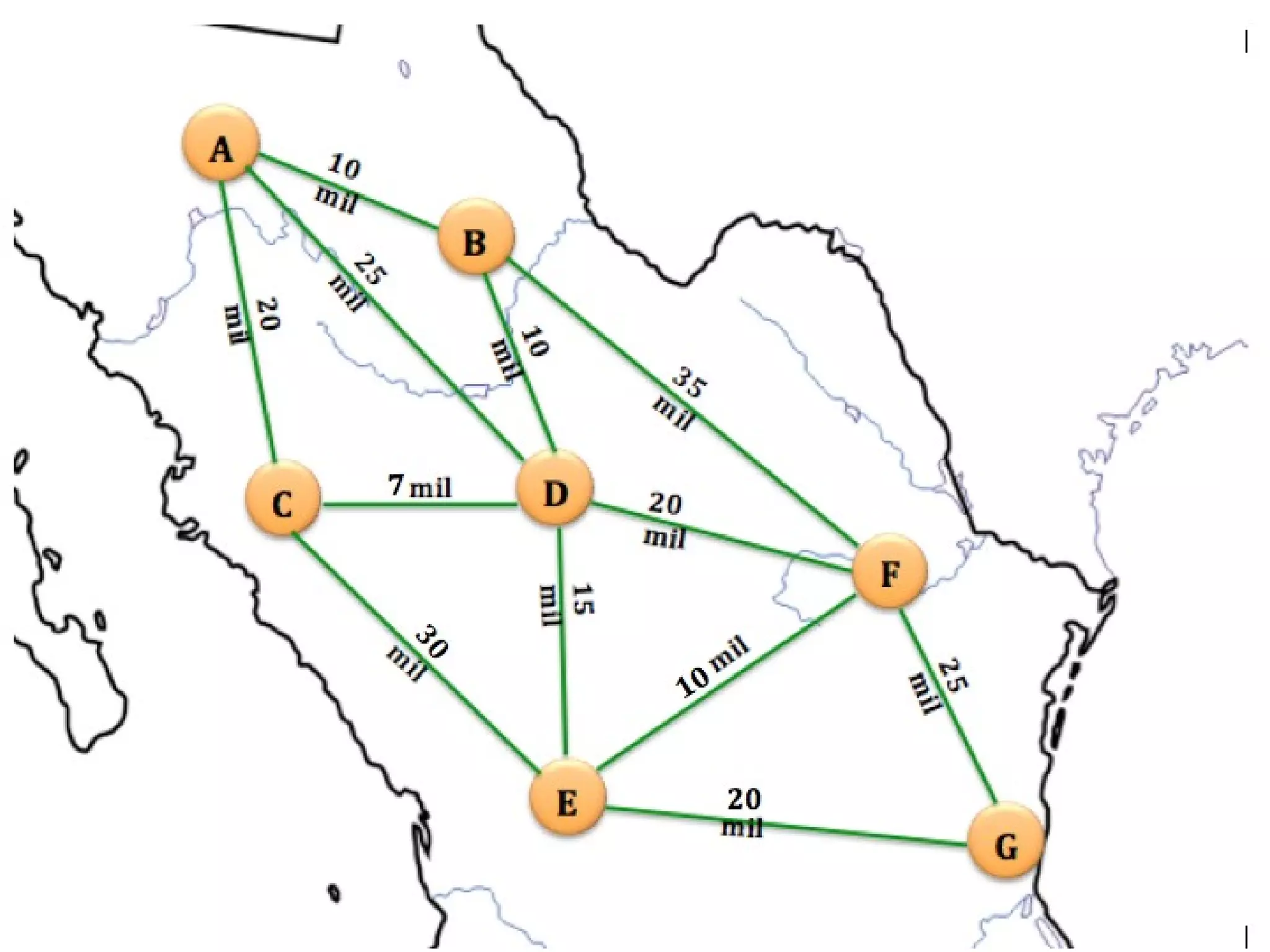
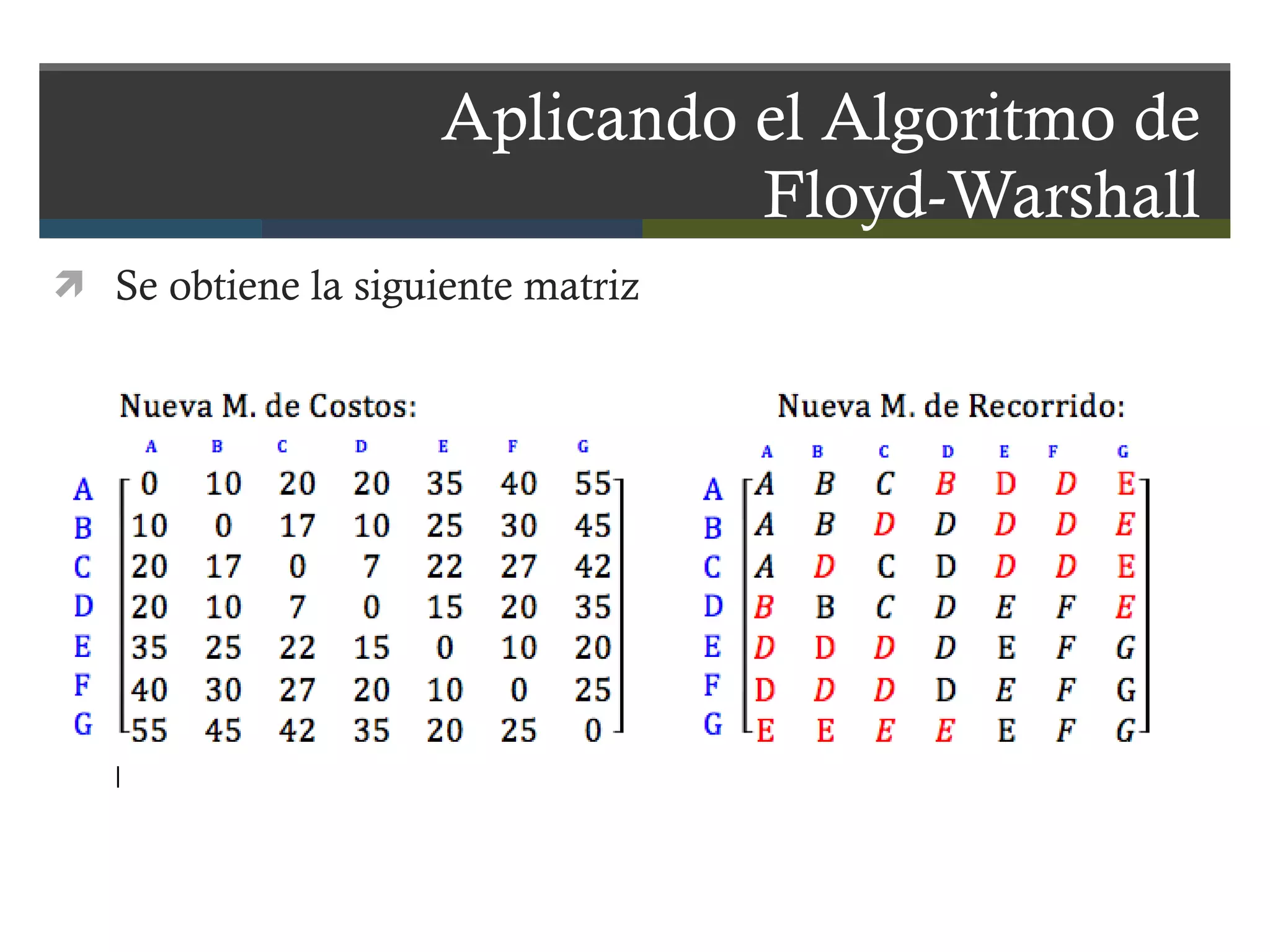
El documento describe el algoritmo de Floyd-Warshall para encontrar el camino más corto entre todos los pares de nodos en un grafo. Se aplica al problema de una empresa con 7 bodegas distribuidoras de aguacate que desea saber el costo mínimo de transporte entre cada par de bodegas. El algoritmo toma como entrada una matriz de adyacencia y mantiene una matriz actualizada con las distancias mínimas entre nodos, resultando en una matriz final con los caminos más cortos. La complejidad del algoritmo es O(N3) donde N es el número de nod

1. UMSNH FIE Análisis de Algoritmos Dra. Karina Mariela Figueroa Mora Algoritmo de Floyd - Warshall Herrera Garcia Jose Juan j [email_address]

2. Problema El problema surge por la necesidad de encontrar el camino mas corto y menos costoso para poder obtener mejores ganacias y ahorrar el mayor tiempo posible. Aplicados por ejemplo a el diseño de rutas de transporte, aproximaciones al problema del viajante de comercio, etc.

3. Algoritmo de Floyd - Warshall 8 de junio de 1936 en Nueva York a 25 de septiembre de 2001 El algoritmo de Floyd-Warshall Encuentra el camino más corto entre todos los pares de nodos o vértices de un grafo. Usa la metodología de Programación Dinámica para resolver el problema. Robert W. Floyd

4. Entrada: una matriz de adyacencia n×n. Cuerpo: la idea es Mantener una matriz con las distancias calculadas hasta ese momento. Resultado: la matriz de resultados contendrá las distancias mínimas y el recorrido.

5. Problema Real La Empresa cuenta con 7 bodegas distribuidoras de aguacate en el país. Los administradores desean saber el costo mínimos de flete de una bodega a otra sin importar la bodega que envía y la bodega que recibe, esto para optimizar recursos a la hora que se transporta producto.

7. Del Grafo obtenemos:

8. Aplicando el Algoritmo de Floyd-Warshall Se obtiene la siguiente matriz

9. Aplicando el Algoritmo de Floyd-Warshall Por ejemplo, si se quiere llevar producto de bodega A a la bodega G: D AG= 55 Con el recorrido A  E  G D AE = 35 Con el recorrido A  D  E D AD = 20 Con el recorrido A  B  D A  B  D  E  G

10. A  B  D  E  G

11. Aplicando el Algoritmo de Floyd-Warshall Por ejemplo, si se quiere llevar producto de bodega A a la bodega G: D FA= 40 Con el recorrido F  D  A D DA = 20 Con el recorrido D  B  A F  D  B  A

12. F  D  B  A

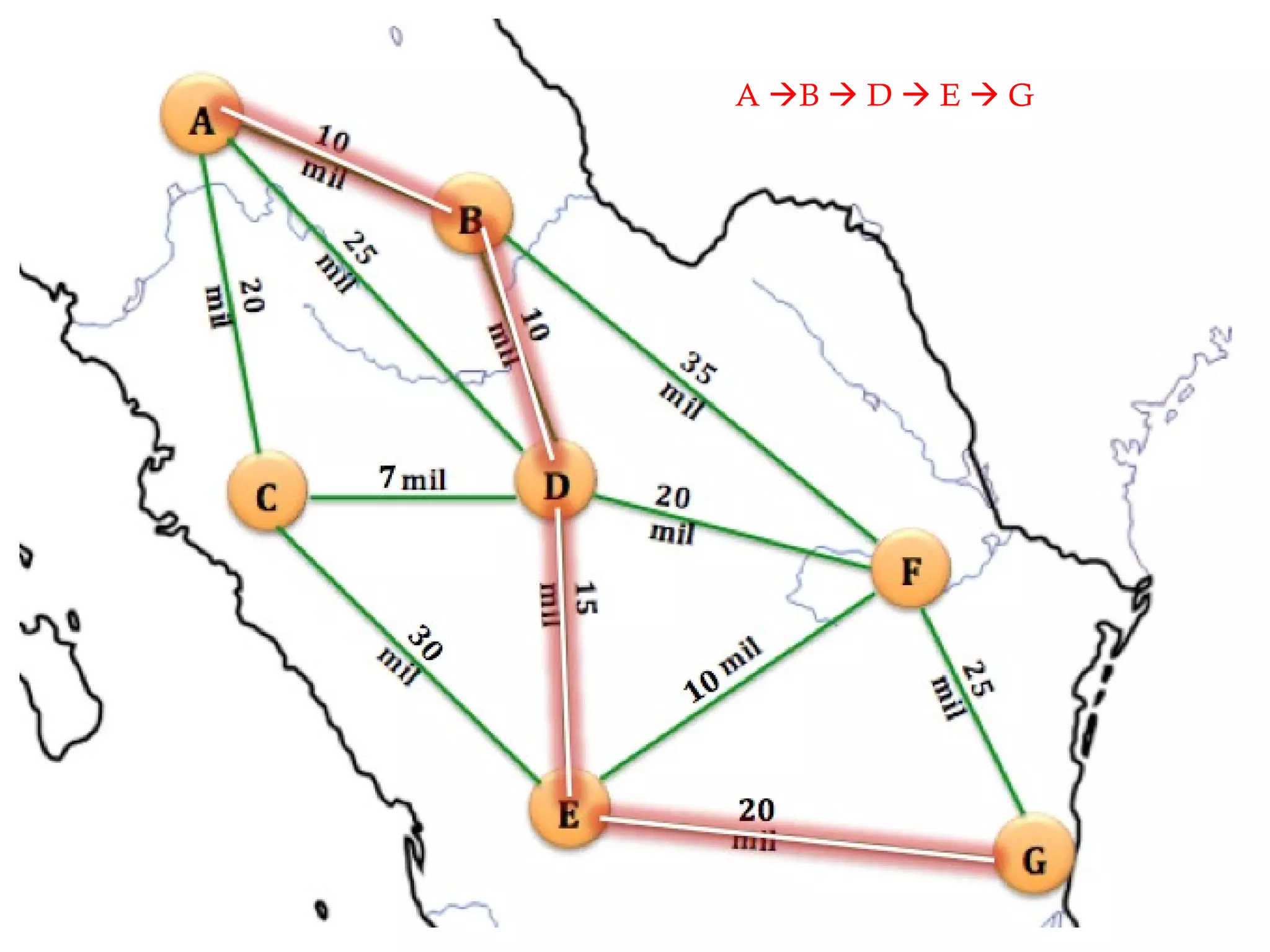
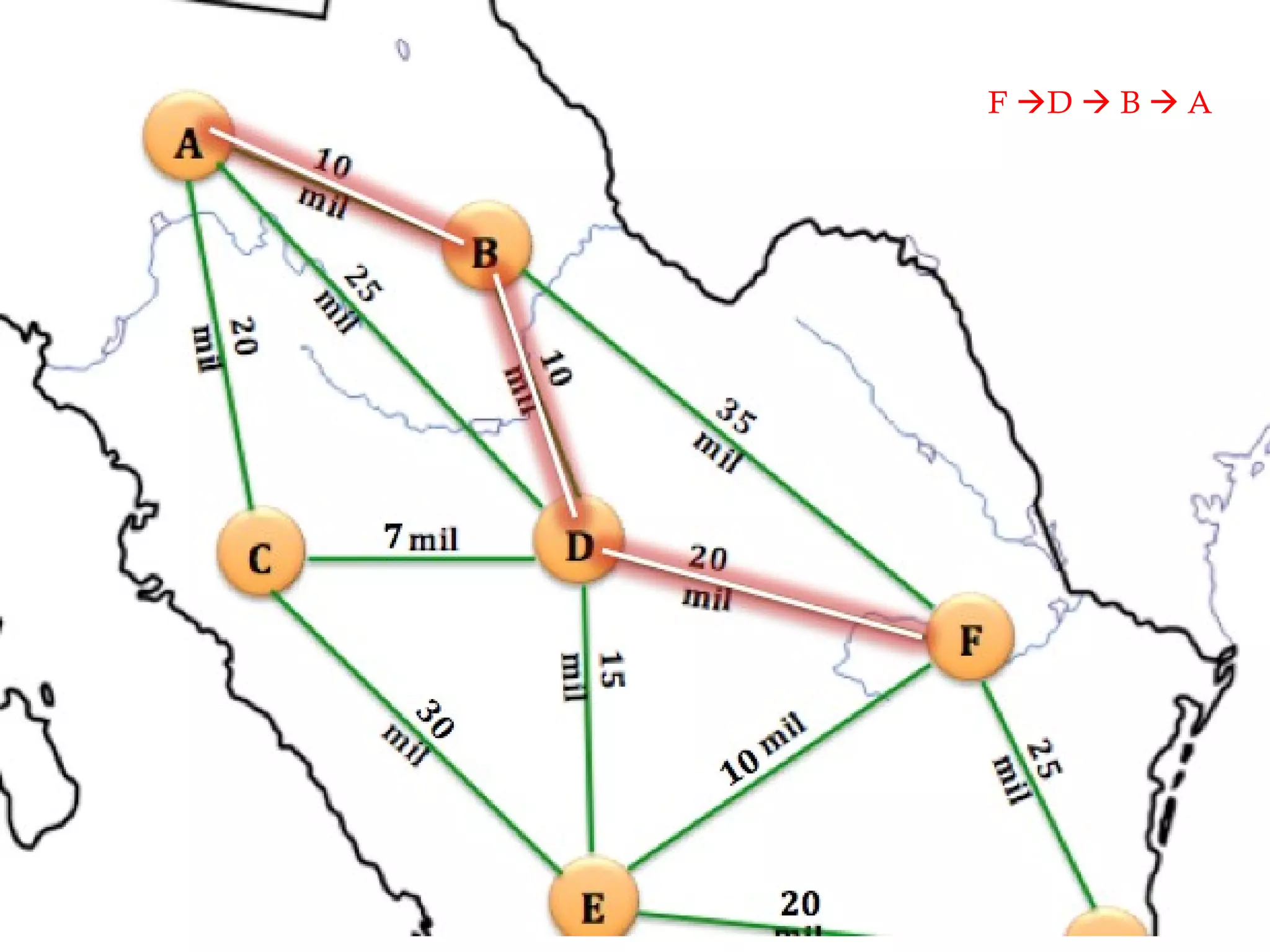
13. Complejidad del algortimo Floyd-Warshall P seducódigo: FloydWarshall (camino[][]) { N=camino.length; para k: = 0 hasta N − 1 //N para i:=0 hasta N − 1 //N P ara j:=0 hasta N−1 //N camino [i][j] = mín ( camino[i][j] , camino[i][k] + camino[k][j] ); } N*N*N = N 3 por lo tanto la complejidad de este algoritmo es O(N 3 ). Donde N es el número de nodos del grafo.

14. Complejidad usando fuerza bruta.

15. Ejemplo: Para 4 nodos, los posibles caminos son: (N-1)!=(3)!=6 Estos caminos son: