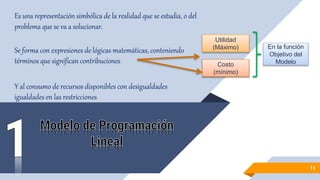
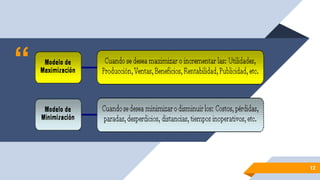
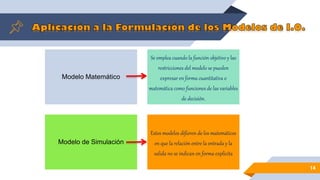
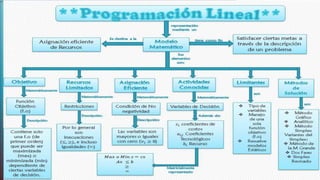
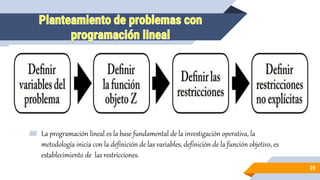
La programación lineal es una técnica matemática utilizada para optimizar el uso de recursos limitados en organizaciones y empresas, desarrollada formalmente en 1947 por George B. Dantzig mediante el método simplex. Esta técnica busca maximizar o minimizar una función lineal sujeta a restricciones, considerada esencial en la investigación operativa y aplicada en diversas áreas como economía, transportes y planificación de producción. Para implementar un modelo de programación lineal, se deben identificar variables, funciones objetivo y restricciones, todo en términos de relaciones lineales.

1. Formulación del
Modelo de
Programacion Lineal
Ing. Sharon Castellón

2. Programación Lineal
Es la interrelaciónde los componentes de un sistema, en
términos matemáticos, ya sea en forma de ecuaciones o
inecuaciones lineales llamado Modelo
de ProgramaciónLineal.
Es una técnica utilizada para
desarrollar modelos matemáticos, diseñada para optimizar
el uso de los recursos limitados en una
empresau organización.
2

3. Programación Lineal
La programaciónlineal es una técnica de optimizaciónque
busca maximizar o minimizar una función lineal, llamada
funciónobjetivo sujeta a restricciones (Álvarez 2005)
Es el enfoque para la soluciónde problemas con miras a
tomar decisiones acertadas, cuyo modelomatemático es la
funciónlineal sujeta a restricciones lineales no negativas
3

4. La programación lineal se concibe formalmente en 1947, pero
existen algunos casos aislados que se remontan a: 1823 con los
trabajos de FOURIER
▰ Joseph Fourier anticipa la programación lineal. Carl
Friedrich Gauss resuelve ecuaciones lineales por
eliminación "gaussiana".
▰ 1902 Gyula Farkas concibe un método para resolver
sistemas de desigualdades.
▰ 1932 con el modelo industrial de Entrada-Salida de W.
Leontier
4
Joseph Fourier

5. La programación lineal empezó a tener mayor auge a finales de
los años 30 y principios de los años 40
 L.V Kantonovich planteó y resolvió un modelo de
planeación y producción
 1941 Hitchcock planteó el problema del transporte
 1945 G.J. Stigter planteó el problema de la Dieta
 John von Neumann, que en 1947 relacionó los problemas
de Programación Lineal con la teoría de Matrices.
5
L.V Kantonovich

6. El Dr. GeorgeB. Dantzing en junio de
1947 desarrolla el modelo general de
la programaciónlineal y el método de
soluciónllamadométodo SIMPLEX.
6
Dr. George B. Dantzing

7. La programación lineal tiene un alto impacto a
escala general, es aplicable a una gran variedad
de problemas organizacionales, se fundamenta
en las siguientes características.
 Se debe establecer algún criterio de decisión
 Las relaciones de las variables deben ser de
tipo lineal.
7

8. ▰ Encontrar soluciones a través de métodos matemáticos
con el uso de sistemas lineales a problemas de carácter
económico- técnico representados por la limitación de
recursos. ‡
▰ Resolver casos de combinación óptima de mezclas de
producción, disposición interna de procesos,
maximización de beneficios, localización, asignación de
recursos, minimización de costos, transporte, entre otros
8

9. o Militares
o Económicos
o Teoría de Juegos
o Transporte
o Medio Ambiente
o Sociología
o Educación
o Gubernamentales
9

10. Qué es un modelo Matemático?
10
Un modelo matemático
es producto de la abstracción de
un sistema real, eliminando las
complejidades y haciendo
suposiciones pertinentes; se aplica
una técnica matemática y se obtiene
una representación simbólica del
mismo.
Un modelo matemático consta al
menos de tres elementos o condiciones
básicas:
• Las Variables de decisión
• La Función Objetivo
• Restricciones.

11. Es una representación simbólica de la realidad que se estudia, o del
problema que se va a solucionar.
Se forma con expresiones de lógicas matemáticas, conteniendo
términos que significan contribuciones:
Y al consumo de recursos disponibles con desigualdades
igualdades en las restricciones.
11
Utilidad
(Máximo)
Costo
(mínimo)
En la función
Objetivo del
Modelo

12. “
12
12

13. Cualquier problema de programación lineal requiere identificar cuatro componentes
básicos:
1. El conjunto de datos.
2. El conjunto de variables involucradas en el problema, junto con sus dominios
respectivos de definición.
3. El conjunto de restricciones lineales del problema que definen el conjunto de
soluciones admisibles.
4. La función lineal que debe ser optimizada (minimizada o maximizada).
13

14. 14
Modelo Matemático
Se emplea cuando la función objetivo y las
restricciones del modelo se pueden
expresar en forma cuantitativa o
matemática como funciones de las variables
de decisión.
Modelo de Simulación
Estos modelos difieren de los matemáticos
en que la relación entre la entrada y la
salida no se indican en forma explicita

15. Se usan para
resolver problemascuantitativos de decisión
en el mundo real.
Algunosmodelos en la cienciade
la administración son llamados modelos
determinísticos.
Modelos Formales
15

16. 16

17. ▰ Planeación de
operaciones y
ventas agregadas
▰ Análisis de la
productividad
▰ Planeación de
productos
17
▰ Rutas de los
productos
▰ Programación de
cuadrillas
▰ Control de
procesos

18. ▰ Control de
inventarios
▰ Programación de
la distribución
18
▰ Manejo de
materiales
▰ Control de
inventarios
▰ Programación de
la distribución
▰ Manejo de
materiales
▰ Control de
inventarios
▰ Estudios para
ubicar la planta

19. Para el planteamiento de un
problema de programación
lineal, se debencumplir y
cinco condiciones básicas:
▰ ‡
Recursos limitados. ‡
▰ Objetivo explícito. ‡
▰ Linealidad. ‡
▰ Homogeneidad.
▰ ‡
Divisibilidad
19

20. ▰ La programación lineal es la base fundamental de la investigación operativa, la
metodología inicia con la definición de las variables, definición de la función objetivo, es
establecimiento de las restricciones.
20

21. ▰ En el caso de problemas de maximización, la solución se determina en la parte
interior formada por el polígono convexo.
▰ En este caso las restricciones serán representadas por la expresión ≤ (menor o
igual que).
▰ Lo que indica que no podrán utilizarse mas recursos que aquellos de los que se
dispone y los coeficientes de las variables del problema de acuerdo a las
necesidades técnicas.
21

22. Donde C1 es el coeficiente de
X1 y C2 es el coeficiente de X2.
Cada recta representa un
conjunto de puntos de
proporcionan un beneficio
idéntico
22

23. 23

24. ▰ En el caso de problemas de minimización se utilizara las
restricciones serán representadas por la expresión ≥ (mayor
o igual que).
▰ La zona de solución se ajusta al conjunto convexo hacia
afuera e identifica un punto extremo (vértice) que minimice
la función objetivo
24

25. 25

26. 26