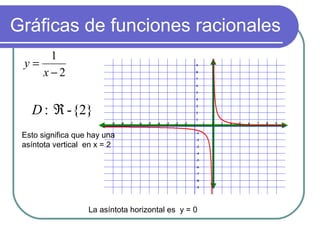
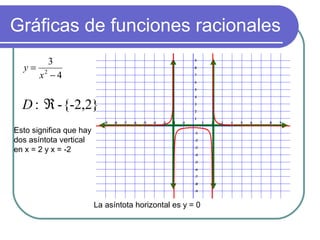
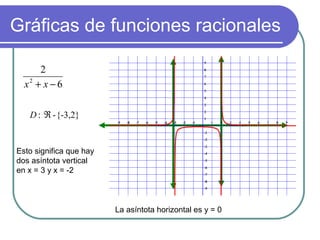
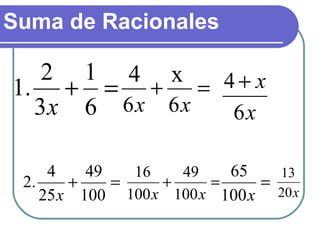
Este documento explica las expresiones racionales, que son aquellas que pueden expresarse como un polinomio dividido por otro polinomio. También define las funciones racionales como expresiones racionales igualadas a y, y describe cómo graficarlas y calcular sus dominios y asíntotas. Finalmente, cubre temas como simplificar, sumar y multiplicar expresiones racionales.

2. Expresión Racional
Una Expresión Racional son aquellas
que se pueden expresar como
polinomio donde hay
polinomio

3. Una función racional
Es una expresión racional
igualada a y. De esta
manera se hace una tabla de
valores para poder hacer la
gráfica.

4. Ejemplos:
6
2
4
3
2
1
2
2
−+
=
−
=
−
=
xx
y
x
y
x
y

5. Dominio
El dominio de una
expresión racional son los
números reales excluyendo
los valores que den cero en
el denominador.

6. Ejemplos:
6
2
4
3
2
1
2
2
−+
=
−
=
−
=
xx
y
x
y
x
y
{2}-: ℜD
{-2,2}-: ℜD
{-3,2}-: ℜD

7. Graficando funciones
racionales

8. Asíntotas
Es una línea imaginaria horizontal o
vertical donde la gráfica se acerca a ella
pero nunca la toca.
¿Cómo se obtiene?
Asíntota vertical es la restricción que
tiene la variable x.

9. Gráficas de funciones racionales
2
1
−
=
x
y
Esto significa que hay una
asíntota vertical en x = 2
La asíntota horizontal es y = 0
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
{2}-: ℜD

10. Gráficas de funciones racionales
4
3
2
−
=
x
y
Esto significa que hay
dos asíntota vertical
en x = 2 y x = -2
La asíntota horizontal es y = 0
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
{-2,2}-: ℜD

11. Gráficas de funciones racionales
6
2
2
−+ xx
{-3,2}-: ℜD
Esto significa que hay
dos asíntota vertical
en x = 3 y x = -2
La asíntota horizontal es y = 0
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9

12. Simplificando expresiones
racionales:
2
126
.2
+
+
x
x
2
)2(6
+
+
x
x
6
2
25
15
.1
b
b
bb
b
⋅⋅⋅
⋅⋅
55
53
b5
3

13. 63
12
.3
2
+c
c
)2(3
223
+
⋅⋅⋅⋅
c
cc
2
4 2
+c
c
9
3
.4 2
−
+
x
x
)3)(3(
3
−+
+
xx
x
)3(
1
−x

15. Multiplicación de
Expresiones Racionales
=
−
⋅
+
14
6
3
12
.1 2
x
xx
)12)(12(
23
3
12
−+
⋅⋅
⋅
+
xx
xx
)12(
2
−x
x
)62(
93
2
.2 +⋅
+
−
m
m
m )3(2
)3(3
2
+⋅
+
−
= m
m
m
3
)2(2 −m

16. Suma de Racionales
=
+
+
+ 3
5
3
2
.1
xx 3
7
+x
=
−
+
− 5
3
5
.2
y
y
y
y
5
4
−y
y

17. Suma de Racionales
=+
6
1
3
2
.1
x
=+
xx 66
4 x
x
x
6
4 +
=+
100
49
25
4
.2
x
=+
xx 100
49
100
16
=
x100
65
x20
13

18. Creditos
Tomado y adaptado de la presentación de la
profesora Carmen Batiz