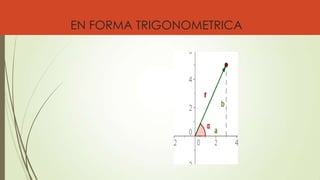
El documento trata sobre los números complejos. Explica que surgen al resolver ecuaciones con raíces cuadradas de números negativos y que la unidad imaginaria i permite definir soluciones. Los números complejos forman un conjunto que amplía los reales. También describe cómo sumar, restar, multiplicar y dividir números complejos, y cómo representarlos en un plano cartesiano o en forma polar.

1. Numeros complejos
A .O D.Ñ J.T y .p

2. ¿Cómo y dónde surgen los números
complejos?
 Los números complejos surgen al resolver ecuaciones algebraicas en las
que hay que calcular raíces cuadradas de números negativos. Como por
ejemplo: x2 + 1 = 0 ,
 Los números complejos sin embargo permiten ampliar aún más el
concepto de "número", definiendo la unidad imaginaria o i como i =√-1, , lo
que significaría que la ecuación anterior sí tendría dos soluciones, que
serían x1= i y x2= - i
 Los números complejos son un conjunto de numeros extensión de los
reales.

3. Qué es la unidad imaginaria?
 La unidad imaginaria es el número y se designa
por la letra i.
 Números imaginarios
 Un número imaginario se denota por bi, donde:
 b es un número real
 i es la unidad imaginaria
 Con los números imaginarios podemos calcular
raíces con índice par y radicando negativo.
 x2 + 9 = 0

4. Se pude operar con ello?
 La suma y diferencia de números complejos se realiza sumando y restando las partes
reales y las partes imaginarias entre sí, respectivamente.
 (a + bi) + (c + di) = (a + c) + (b + d)i
 (a + bi) − (c + di) = (a − c) + (b − d)i
 Ejemplo:
 (5 + 2i) + ( − 8 + 3i) − (4 − 2i ) =
 = (5 − 8 − 4) + (2 + 3 + 2)i = −7 + 7i

5. Números complejos en forma polar
CONSTAN DE : El módulo de un número complejo es el módulo del
vector determinado por el origen de coordenadas y su afijo. Se designa
por |z|.
Argumento: es el Angulo que forma el vector con el eje real

6. EN FORMA TRIGONOMETRICA

7. Cómo se representan en un sistema de
ejes cartesianos?
 Se puede representar una función en el plano haciendo corresponder a
cada par del grafo un punto determinado, marcando en el eje de
abscisas el valor de su variable y en el de ordenadas
 Representación de números complejos

8. EJERCIOS DE NUMEROS COMPLEJOS
x** +27=3
X**=3-37
X**=-25
X=√-25 ―√(25)(-1) 5√-1 5і
=5і

9. Diseñar
 Desde el principio, usted tendrá acceso a
atractivos temas panorámicos que podrá
cambiar fácilmente para adecuarlos a su
estilo. Todos los temas incorporan diversas
variantes de color que puede mezclar y
combinar.
 Nuevas funciones como Combinar formas y
un cuentagotas de coincidencia de
colores abren todo un mundo de nuevas
posibilidades para sus diseños.
 Alinee sus diseños, fotos y diagramas
perfectamente y en cuestión de segundos
mediante guías de alineación y guías

10. Impresionar
 La mejorada vista Moderador incluye nuevas
herramientas para ayudarle a tenerlo todo
controlado. La nueva Ampliación automática aplica
de forma instantánea la configuración más
adecuada, por lo que usted podrá centrarse en
hablar en lugar de en la pantalla.
 Zoom de diapositiva: le ayuda a centrar la atención de
su público en sus ideas. Simplemente haga clic para
acercar o alejar un diagrama o gráfico en particular.
 Explorador de diapositivas: función que permite al

11. Trabajar en equipo
 Modifique presentaciones con otros
usuarios que trabajen a la vez desde
diferentes PC y mantenga
conversaciones con comentarios
mejorados.
 Compartir documentos en línea es
sencillo. Aunque su público no
tenga PowerPoint, simplemente
proyecte la presentación en su
explorador mediante Presentar en

12. PowerPoint 2013
Diseñe atractivas presentaciones de
manera intuitiva; comparta
presentaciones y trabaje fácilmente
con otros usuarios; y ofrezca una
imagen profesional mediante
herramientas de presentación
avanzadas.
Obtenga más información en el Centro de introducción a PowerPoint