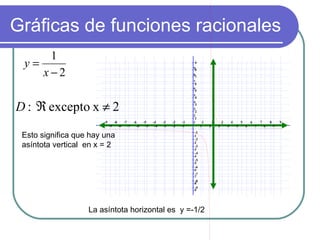
Este documento define funciones racionales y explica cómo graficarlas y resolver ecuaciones racionales. Las funciones racionales son expresiones donde el polinomio está en el numerador y el denominador. Para graficarlas, se identifican las asíntotas verticales y horizontales. Para resolver ecuaciones racionales, se factoriza, se halla el denominador común, y se multiplica la ecuación por este para obtener una expresión no racional que puede resolverse. También explica operaciones básicas como suma, resta, multiplicación y división de expresiones rac

1. Funciones Racionales Por: Pofa. Carmen Batiz UGHS

2. Definición: Una Expresión Racional son aquellas que se pueden expresar como polinomio donde hay polinomio variables en el denominador.

3. Ejemplos:

4. Una función racional Es una expresión racional igualada a y. De esta manera se hace una tabla de valores para poder hacer la gráfica.

5. Ejemplos:

6. Dominio El dominio de una expresión racional son los números reales excluyendo los valores que te den cero en el denominador.

7. Ejemplos:

8. Graficando funciones racionales

9. Asíntotas Es una línea imaginaria horizontal o vertical donde la gráfica se acerca a ella pero nunca la toca. ¿Cómo se obtiene? Asíntota vertical es la restricción que tiene la variable x. Asíntota horizontal es cuando se le da valor de cero a la variable x y se despeja para y.

10. Gráficas de funciones racionales Esto significa que hay una asíntota vertical en x = 2 La asíntota horizontal es y =-1/2

11. Gráficas de funciones racionales Esto significa que hay dos asíntota vertical en x = 2 y x = -2 La asíntota horizontal es y = -3/4

12. Gráficas de funciones racionales Esto significa que hay dos asíntota vertical en x = 3 y x = -2 La asíntota horizontal es y = -1/3

13. Simplificando expresiones racionales:

14. Cont.

16. Operaciones con Expresiones Racionales

17. Multiplicación de Expresiones Racionales

18. División de Racionales

19. Suma de Racionales

20. Suma de Racionales 4 x 16 49

21. Resta de Racionales 14y 2 9

22. Resta de Racionales 3(y + 4) 5

23. Resolver ecuaciones racionales Para resolver ecuaciones racionales se debe: factorizar todas las expresiones que no lo están. hallar el denominador común de la ecuación. multiplicar toda la ecuación por el denominador común hallado.(Al multiplicar se cancelarán todos los factores comunes y obtendrás una expresión no racional) simplificar y factorizar de ser necesario. hallar los valores de la variable utilizando la Propiedad de la Igualdad de Cero.

24. Ejemplos: 1er paso: factorizar todas las expresiones que no lo están. 2do paso: Hallar el denominador común de la ecuación. 3er paso: multiplicar toda la ecuación por el denominador común hallado.(Al multiplicar se cancelarán todos los factores comunes y obtendrás una expresión no racional) .

25. Ejemplos: cont

26. Ejemplos: 1er paso: factorizar todas las expresiones que no lo están. 2do paso: Hallar el denominador común de la ecuación. 3er paso: multiplicar toda la ecuación por el denominador común hallado.(Al multiplicar se cancelarán todos los factores comunes y obtendrás una expresión no racional) .

27. Ejemplos: cont.