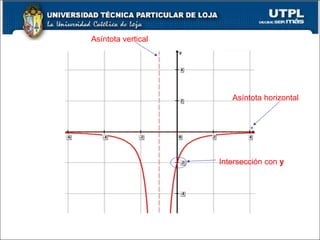
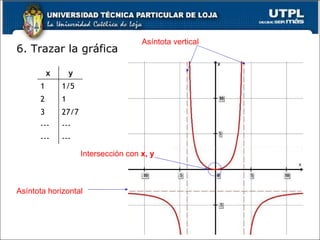
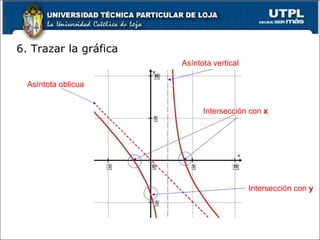
El documento explica las funciones polinómicas y racionales, destacando cómo graficarlas y determinar su comportamiento a través de intersecciones, asíntotas y signos algebraicos. Se detallan procedimientos para identificar asíntotas verticales y horizontales, así como reglas para graficar funciones racionales. Además, se menciona la existencia de asíntotas oblicuas cuando el grado del numerador es mayor que el denominador.

1. ESCUELA : NOMBRES: FUNDAMENTOS MATEMÁTICOS FECHA : Ciencias de la Computación Ing. Ricardo Blacio ABRIL - AGOSTO 2010

2. 4. Funciones polinomiales y racionales Una función polinomial tiene la forma: Si el coeficiente se dice entonces que la función polinomial es de grado n, el número se denomina coeficiente principal del polinomio. Generalmente, a medida que el grado aumenta, la gráfica es más complicada.

3. Se puede obtener una gráfica totalmente precisa utilizando el procedimiento sugerido a continuación: Calcule  (  x) para determinar si la gráfica tiene alguna simetría. Calcule el intersecto  (0) en y. Factorice el polinomio. Determine los intersectos en x, hallando las soluciones reales de la ecuación  (x)  0. Trace una recta numérica. Determine los signos algebraicos de todos los factores entre los intersectos en x. Esto indicará dónde  (x)  0 y donde  (x)  0. Grafique la función utilizando los resultados de los pasos 1 – 5 y marcando puntos adicionales donde sea necesario.

4. En los casos en los que  (x) son positivos (  (x)  0), la gráfica de la función está por encima del eje x. La gráfica de la función esta por debajo del eje x, en aquellos intervalos donde los valores de  (x) son negativos (  (x)  0).

5. Funciones racionales Las funciones racionales se definen en términos de cocientes de polinomios. En general, una expresión R es una función racional sí: g(x), h(x) son polinomios; el dominio de F es el conjunto de todos los números reales tales que h(x)  0. Las funciones racionales son continuas para todo valor de x, con excepción de aquellos para los que el denominador h(x) es cero.

6. Asíntotas Las rectas fijas a las que se aproxima una gráfica, se llaman asíntotas. Asíntotas verticales Se dice que una recta x  a es una asíntota vertical para la gráfica de una función  sí.

7. Asíntotas horizontales Sea R una función racional definida como cociente de dos polinomios de la forma: Teoremas: 1.- Sí m< n, el eje x (y = 0) es una asíntota horizontal. 2.- Sí m =n, la recta y=a m /b n es una asíntota horizontal. 3.- Sí m > n, no hay asíntotas.

8. Gráfica de funciones racionales Si F(x)= g(x)/h(x) donde g(x) y h(x) son polinomios se debe seguir las siguientes pautas: Encontrar las intersecciones con x, haciendo g(x) = 0. Hallar la asíntota vertical resolviendo h(x)=0. Encontrar las intersecciones con y, obteniendo F(0), trazamos la intersección (0,F(0)). Aplicar teorema de asíntotas horizontales y=c. Si existen asíntotas horizontales determinar si corta la gráfica con f(x) = c. Trazar la gráfica en cada región.

9. 1. Intersección con x hacer y = 0 Ejercicios. Trace la gráfica de f a.- 0 = - 2 No hay intersección con x 2. Asíntota vertical x + 1 = 0 x = - 1 3. Intersección con y hacer x = 0 = - 2

10. 4. Asíntota horizontal 1 1 < 2 Entonces el eje x es la asíntota horizontal Teorema 1 5. No aplica Este paso se da cuando se tiene el teorema 2 en el paso anterior. 6. Trazar la gráfica x y 1 -1/2 2 -2/9 3 -1/8 -2 -2 -3 -1/2

11. Asíntota vertical Asíntota horizontal Intersección con y

12. 1. Intersección con x hacer y = 0 b.- 0 = 3x 2 2. Asíntota vertical 16 – x 2 = 0 3. Intersección con y hacer x = 0 = 0 x = 0 – x 2 = - 16 x 2 = 16 x = ± 4

13. 4. Asíntota horizontal 2 = 2 La recta y=a m /b n es la asíntota horizontal Teorema 2 5. Determinar si la asíntota horizontal corta la gráfica y=3 /-1 y= -3 f(x) = c 3x 2 = - 48 + 3x 2 0 = - 48 La gráfica no cruza la asíntota horizontal y = -3 porque f(x) = - 3 no tiene solución real.

14. 6. Trazar la gráfica Asíntota vertical Asíntota horizontal Intersección con x, y x y 1 1/5 2 1 3 27/7 --- --- --- ---

15. x 2 - 2x – 8 = 0 (x - 4) (x + 2) = 0 x = 4 x = - 2 - x + 2= 0 - x = - 2 x = 2 = - 4 c.- 1. Intersección con x hacer y = 0 2. Asíntota vertical 3. Intersección con y hacer x = 0

16. 1 2 > 1 4. Asíntota horizontal No hay asíntota horizontal Teorema 3 5. No aplica 6. Asíntota oblicua Una función racional tiene una asíntota oblicua cuando el grado del numerador es una unidad mayor que el grado del denominador. 1

17. x 2 - 2x – 8 - x + 2 - x 2 + 2x - 8 - x Uno de los métodos más usados es la división sintética para hallar la ecuación de la asíntota oblicua. Este cociente es la ecuación de la asíntota. y = - x x y 0 0 1 -1 2 -2 -1 1 -2 2 --- ---

18. Asíntota vertical Intersección con y Asíntota oblicua Intersección con x 6. Trazar la gráfica

19. Ing. Ricardo Blacio Docente – UTPL Correo electrónico: [email_address]