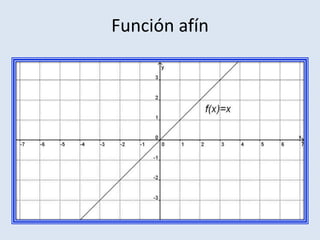
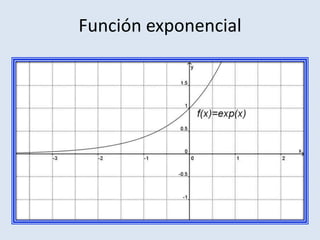
Este documento describe diferentes tipos de funciones matemáticas y sus aplicaciones, incluyendo funciones constantes, afines, lineales, irracionales, racionales, exponenciales, logarítmicas, seno, coseno y tangente. Cada función se utiliza para representar matemáticamente diferentes relaciones y fenómenos del mundo real como la velocidad, precios, períodos de péndulos, leyes de la química, crecimiento de poblaciones, terremotos, ondas eléctricas y más.

1. Álbum de fotografías
por Humberto Álvarez E.

2. Función matemática
A partir de Descartes hasta Dirichlet se obtiene o deriva el concepto
actual de función.
Una función es una relación entre dos conjuntos, A y B, en la que existe
una regla de asociación, y que además, cada elemento del conjunto A
se relaciona con uno y solo uno del rango (subconjunto de B).
El conjunto A es el dominio de la función y el conjunto B es el
codominio.
Son muchas las situaciones reales en las que se utiliza el concepto de
función para describirlas matemáticamente, es decir, cuantifican y
representan la realidad.
Por ejemplo, la función constante puede expresar, y representar gráfi-
camente, el comportamiento de la velocidad invariable respecto al
tiempo para un móvil que se desplaza con movimiento rectilíneo
uniforme.

3. Función constante

4. Con la función afín se logra expresar relaciones directamente proporcionales,
tales como precios y unidades vendidas.
Insistiendo en las relaciones de la física con las matemáticas, con esta función
también se obtiene, en el movimiento rectilíneo uniforme, una relación entre
el desplazamiento de un móvil y el tiempo que invierte en realizar este
desplazamiento.

5. Función afín

6. Se recurre a la función lineal en eventos donde se relacionan cantidades
directamente proporcionales con un tope preestablecido ( en el eje vertical
del plano cartesiano), como por ejemplo el precio que se cobra por el
consumo de agua, en metros cúbicos; en el cual se establece un valor fijo,
aunque no se haya consumido ninguna cantidad de agua.

7. Función lineal

8. La función irracional (raíz cuadrada) tiene aplicabilidad cuando se trata de
expresar el período de un péndulo simple en función de su longitud:
T 2 l donde T período del péndulo y l longitud

9. Función irracional

10. La función racional está presente en la química: la ley de Boyle dice que
la presión y el volumen son inversamente proporcionales para un gas a
temperatura constante:
K
P donde P presión K temperatura constante y V volumen
V
Esta es fórmula es válida sólo para la rama de la hipérbola que está en el
primer cuadrante, es decir, para aquellos valores positivos del volumen y
de la presión.

11. Función racional

12. La función exponencial tiene diferentes aplicaciones relacionadas con el
crecimiento de poblaciones o cultivo de bacterias, interés del dinero
acumulado en el tiempo, desintegración radiactiva, entre otras.
Por ejemplo para determinar la cantidad de dinero acumulado o el valor
futro se utiliza la siguiente fórmula:
A Pe it
Donde A cantidad de dinero acumulado o valor futuro
P capital invertido
i int erés anual
t número de años

13. Función exponencial

14. La magnitud de un terremoto se mide a través de la escala de Richter, cuya
expresión está determinada por una función logarítmica:
R log A
A0
Donde A0 es una constante
y A es la intensidad (es la amplitud de un sismógrafo estándar,
ubicado a 100 km del epicentro del terremoto)
El PH determina la concentración de iones de hidrógeno, utilizando
una función logarítmica es posible realizar este cálculo:
PH log( H ) donde H es la concentración de iones de hidrógeno

15. Función logarítmica

16. La Función seno es otro recurso especial para representar toda clase de
ondas. La siguiente aplicación demuestra la gran utilidad de esta función:
“ El estudio de las corrientes sinusoidales, es importante porque el teorema
de Fourier asegura que siempre se podrá analizar una corriente periódica
como suma de infinitas corrientes sinusoidales.
Si la fuerza electromotriz armónica se aplica a un circuito cerrado,
mediante consideraciones físicas puede demostrarse que la intensidad de
corriente generada tiene la forma la forma:
I I0 sen wt
Donde Io y son dos constantes que dependen de los elementos en el
circuito (condensadores, resistencias e inducciones) y que reciben el
nombre de intensidad máxima y ángulo de fase, respectivamente”.
http://www.csi-csif.es/andalucia/modules/mod_ense/revista/pdf/Numero_16/SILVIA_BORREGO_1.pdf

17. Función seno

18. La función coseno:
Al cerrarse un circuito eléctrico con una bobina y un condensador cargado,
provoca un flujo de carga por la bobina. Dicha carga va variando a medida que
transcurre el tiempo y la función que describe la relación entre la carga del
circuito y el tiempo es:
Q(t) = A.cos( wt + d)
Donde A, w y d son constantes y t es el tiempo.

19. Función coseno

20. La importancia que tiene la razón o función trigonométrica tangente en el
concepto de derivada y determinación de las direcciones de diferentes des-
plazamientos o de fuerzas aplicadas a un objeto es suficiente para tener pre-
sente esta función como aplicación fundamental en la ciencia.

21. Función tangente